基于SEIR模型的COVID-19传播过程及网约车应对策略研究

摘 要： 2019年末突然爆发的新型冠状病毒（COVID-19）肺炎严重影响到居民的日常生活。网约车作为公共交通系统的补充，在大中运量公共交通停止运营期间，为居民的刚性出行需求提供了保障性服务。本文基于SEIR传染病模型模拟病毒传染的传播过程，通过对比分析说明减少人员接触对遏制病毒传播的重要性。健康码作为一个数字抗疫亮点，考虑到健康码为红色的乘客携带病毒的可能性较高，本文提出对其进行一对一接送策略，在保证乘客出行需求的前提下，降低其他乘客感染病毒的风险，并利用二元选择模型中的logit模型来预测网约车司机运送红码乘客的概率。最后基于SEIR模型传播过程，分别从控制车内的人员数量、缩短乘客的出行时间以及车辆的防疫措施这三方面对疫情期间网约车出行提出应对策略。

关键词： SEIR传染病模型; 病毒传播; 网约车运营管理; 二元选择模型

COVID-19 propagation process based on SEIR

model and online car-hailing response strategy

CHEN Jingyi

（Business School， University of Shanghai for Science and Technology， Shanghai 200093， China）

【Abstract】The sudden outbreak of COVID-19 at the end of 2019 has seriously affected residents' daily life. As a supplement to the public transport system， online car-hailing provides guaranteed services for residents' rigid travel demands during the shutdown of large and medium volume public transport. Based on the SEIR infectious disease model， this paper simulates the transmission process of virus infection and illustrates the importance of reducing human contact to contain the transmission of virus through comparative analysis. As a digital anti epidemic window， considering the fact that passengers with a red health code are more likely to carry the virus， this paper puts forward one-on-one transport strategy， on the premise of guaranteeing the passenger travel demand， reduces the risk of other passengers infected with the virus， and by using the logit model of binary choice model to predict the probability about car driver carrying red-code passengers. Finally， based on the propagation process of SEIR model， the countermeasures for online ride-hailing during the epidemic period are proposed from three aspects： controlling the number of passengers in the car， shortening the travel time of passengers and epidemic prevention measures of vehicles.

【Key words】SEIR model; virus transmission; online car-hailing operation management; binary choice model

0 引 言

2020年初新型冠狀病毒肺炎（以下简称‘新冠肺炎）突然爆发，研究表明，新冠肺炎的传播途径主要是飞沫传播和间接接触传播[1]。为了最大限度遏制疫情蔓延，中国交通运输部、卫健委等相关部门采取了一系列的措施。由于疫情爆发正值春运期间，人口流动量极大。为了减少人员的流动，遏制病毒传播，仅以武汉为例，武汉市自2020年1月23日10时起，全市的公交、地铁、长途客运等暂停运营，离汉通道暂时关闭。为了保障社区居民应急出行，武汉市交通运输局从9家巡游出租车和网约车公司共征集车辆6 000辆，为居民应急出行提供服务[2]。网约车以互联网技术为依托构建服务平台，整合供需信息，车辆和驾驶员需要符合平台的条件，是一种提供非巡游的预约出租车服务的交通工具[3]。2015年之后，网约车作为公共交通系统的补充在国内迅猛发展，在大中运量公共交通停止运营期间，为居民的刚性出行需求提供了保障性服务。

面对疫情给交通运输业带来的冲击，诸多学者对疫情期间的交通出行进行了研究。高永等人[4]对东北某市新冠疫情爆发前后一段时间内网约车数据进行分析，发现受疫情影响网约车的订单数量和司机出车数量均大幅下降，且与疫情的确诊人数呈正比例相关关系。吴楠等人[5]以武汉市公共交通为研究对象，对疫情期间公交现状及出行特征进行分析，推断出在疫情持续期大多数民众仍对公共交通方式的暴露风险感到担忧，公共交通客流回流需要缓冲期，最后从需求与供给的角度出发，制定了武汉市疫情后公共交通组合运营策略。张宇等人[6]建立了基于SEIR模型的交通工具疫情传播模型与沿线路疫情传播模型，对新冠疫情是如何通过交通线路向外传播扩散的过程进行了完整的描述。李健等人[7]提出了一种面向传染病疫情防控的公共交通运行决策支持系统框架，其研究成果对传染病疫情防控具有实用价值。刘海平等人[8]将室内病毒通过飞沫在空气中传播的理论应用于公共汽车车内空间，有针对性地提出公共汽车交通疫情防控应对策略。上述学者的研究成果对疫情后网约车的运营策略具有重要的参考意义。本文对病毒传播过程进行分析后，提出对红码乘客的出行进行一对一接送的策略，并预测网约车司机接送红码乘客的概率。

1 新冠疫情传播过程分析

在社会发展过程中人们一直在与传染病作斗争，如SARS病毒、埃博拉病毒等[9-10]。相关研究表明，新型冠状病毒具有潜伏期，本文利用含有易感状态、潜伏状态、感染状态以及康复状态的SEIR模型[11]，能够更加准确地描述新型冠状病毒的传播过程。

1.1 基于SEIR的传染病预测模型

根据已有的研究发现，COVID-19病毒具有1～14天的潜伏期，平均潜伏期是5.2天，病毒在潜伏期内也具有传染性[12]。经典的传染病模型有SI模型、SIR模型、SIS模型和SEIR模型[13]。由于新型冠状病毒具有潜伏期，当易感者与病人接触后会成为病毒携带者，将此类人群定义为潜伏者“E”。结合本次疫情分析，SEIR模型更加符合新型冠状病毒的传染特征。因此从病毒具有潜伏期的角度考虑，本文利用含有潜伏期的SEIR模型对病毒传播过程进行分析，模型的基本流程图如图1所示。

研究中需用到的符号定义见表1。在此基础上，对模型建立展开探讨论述。利用非线性常微分方程来描述病毒在一个群体中的传播，易感者表示为：

其中，上述模型不考虑人口的出生率和自然死亡率，不考虑人口的迁入和迁出对新冠病毒肺炎的影响。

1.2 病毒传播过程分析

依据上述模型，利用Matlab软件进行求解，对网约车接送初始易感人群总数为100人时的新型冠状病毒传播過程进行模拟，假设初始传染者人数为1人，病毒潜伏期为14天。参数β值是指易感者在单位时间内与感染者接触后被感染的概率，本文将采取防疫措施之前的易感者被感染者感染的概率设定为0.03;参数β1是指易感者在单位时间内与潜伏者接触后被感染的概率，将其值设定为0.02。得到当接触人数分别为20人、10人、5人、1人时，新冠病毒在传播过程中不同人群随时间演化的结果，如图2～图5所示。

对图2进行分析后可以得到，在病毒传播初期会迎来一个爆发期，潜伏者和感染者的数量是一个先增加、后减少的过程，在第20天左右到达高峰值，之后开始下降。而易感者的人数会在大幅度降低后趋于平稳接近于0，康复者的曲线逐渐上升后趋于平稳。将图2～图5进行对比分析后发现，当接触人数r值减少时，潜伏者和感染者的增长趋势变缓，高峰值降低，到达高峰的时间逐渐后移，这一结果将会给医疗救助提供缓冲期。

图2～图5是疫情爆发初期人们未采取措施时的预测趋势图。在疫情爆发后，国家卫健委提出佩戴口罩可以降低病毒传播风险，降低感染率β。本文将采取防疫措施之后易感者被感染者感染的概率（参数值β）设定为0.02，将易感者单位时间内与潜伏者接触后被感染的概率（参数β1）设定为0.01。得到当接触人数分别为20人、10人、5人、1人时的新冠病毒传播预测趋势图，如图6～图9所示。

将采取防疫措施之后的预测趋势图与未采取任何措施的预测趋势图进行对比分析，发现采取防疫措施后潜伏者和感染者的预测趋势图高峰值明显降低，增长趋势变缓且到达高峰的时间后移。若采取防疫措施，且易感人数为100人，接触人数为1时，从图9可看出感染曲线几乎消失。因此，从上述分析结果来看，倘若易感人群有100人，在做好防疫措施的前提下，网约车每次只接送1人，被病毒感染的概率极低。

2 关于红码乘客的车辆匹配模型

新冠肺炎疫情期间，公共交通在一段时间内处于停滞状态，网约车在此期间为保障居民的出行需求发挥了重要作用。为了降低出行风险，确保网约车安全有序运营，在满足居民出行需求的同时，结合疫情防控要求，车辆需要定时通风与消毒，司机需要佩戴口罩和手套进行防护。“滴滴”为了保障网约车的司乘安全，为坚守在抗疫一线的网约车免费安装车内防护膜，尽可能预防飞沫传播[14]。乘客在乘坐网约车时需要出示健康码，乘车期间要全程佩戴口罩，进行体温测量以及扫码登记。

自疫情爆发以来，健康码在掌握全民疫情风险信息中起到了重要作用。杭州率先推出的数字化防疫措施，能够快速筛选出健康人群进行风险预防。健康码实行“红、绿、黄”三色码的动态管理，颜色代表人员不同的风险等级，绿码亮码通行，一人一码，是疫情期间个人通行的电子凭证。若出行者曾与确诊或疑似病例在一起，或来自重点疫区，都会影响健康码的颜色[15]。考虑到红码乘客在出行时具有较大的风险，本文采取一对一接送的策略。为了降低网约车与乘客之间的接触时间，减少病毒交叉感染的风险，本文根据红码乘客所在位置安排车辆，使最终完成运输任务的总时间最短。假设共有n辆车接送n名红码乘客，每辆车每次只能接送一名乘客，第i辆车运送第j名乘客的时间为tij，用0-1变量Xij表示分配情况：

Xij=1 若第i辆网约车运送第j名乘客

0 若第i辆网约车未运送第j名乘客

上述问题的数学模型表示如下：

其中，约束（2）和（3）是唯一性约束，代表每辆车只能接送一名乘客，每名乘客只能被一辆车服务。

3 构建二元logit模型预测网约车接送红码乘客概率

在经典的计量经济学模型中，被解释变量通常被假定为连续变量，但是在实际分析中，作为研究对象的被解释变量的观测值经常是离散的，这种模型被称为离散被解释变量模型。而以决策结果作为被解释变量建立的计量经济学模型被称为离散选择模型[16]。离散选择模型起源于1860年费希纳进行的动物条件二元反射研究，沃纳在1962年利用离散选择模型研究公共交通工具和私人交通工具的选择问题。在20世纪70年代到80年代，离散选择模型被广泛应用于交通、就业等经济决策领域的问题[17]。而在疫情期间网约车会在何种情景下接送红码乘客值得研究，本文将利用二元选择模型进行模拟仿真实验，并对司机是否接送红码乘客的选择行为进行预测。

3.1 模型建立背景

二元选择模型在选择行为的研究中应用广泛。王云泽等人[18]利用二项logistic模型建立驾驶人分流选择行为概率模型，分析驾驶员在互通式立交分流选择行为所受因素的影响。向红艳等人[19]利用效用最大化理论对出行者市内出行阶段和城际出行阶段的选择行为建立巢式logit模型。杨少伟等人[20]对驾驶员收费车道选择行为的规律特征进行研究，并建立了选择行为的二元logit模型。张宁等人[21]对出行特征影响因素进行分析，利用多项logit模型建立居民出行方式选择模型。孙启鹏等人[22]运用随机效用理论和离散选择模型，建立了基于动态广义费用的交通方式选择logit模型。上述学者的研究具有重要的参考意义。

3.2 模型建立及结果分析

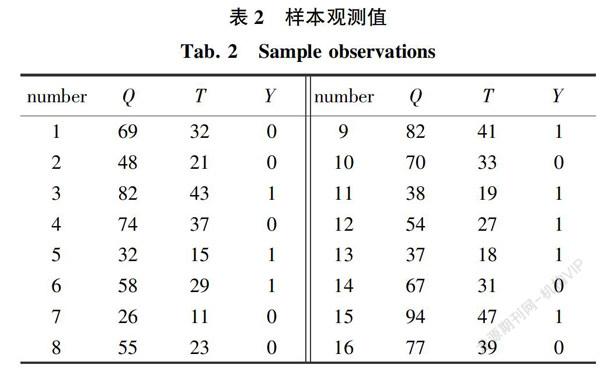
由于疫情的突然爆发，关于网约车是否会接送红码乘客，在目前的实际运营中尚未有确切的数据，因此难以获得具体数据。在上述背景下，本文采取随机生成数据的方式，通过进行模拟仿真实验，来预测司机接送红码乘客的概率。其中，利用二元选择模型中的logit模型预测网约车司机是否接送红码乘客。利用二元离散变量Y来表示网约车司机是否运送红码乘客，若运送乘客，则Y=1;若未运送乘客，则Y=0。本文共选择16个样本，数据中包含运送红码乘客增加的收益Q以及运输红码乘客后因需要去消毒多花费的时间T。样本观测值见表2。

利用Eviews软件中的logit模型估计方法，其中Y为被解释变量，常数项、Q、T为解释变量，对于异方差采用White修正，得到的输出结果如图10所示。

图10的第一部分显示了模型估计的基本信息，包括模型估计方法、使用样本、与迭代收敛相关的信息;第二部分是模型的估计结果，第三部分是二元选择模型中因变量的频率分析。从图10中可以得到拟合优度McFadden R-squared的值为0.484 447;Prod（LR statistic）的值为0.004 642，远远小于0.05，说明拒绝原假设，意味着收益和时间这两个变量对被解释变量司机是否运输红码乘客具有显著性影响。因为LR statistic=10.745 38，>x20.05（2）=5.991 47，所以在给定显著性水平a=0.05拒绝原假设H0：β2=β3=0，表明离散选择模型中所有解释变量的系数不全为0。根据表2可得到模型的回归结果如下所示：

当收益Q和时间T已知时，利用上述方程可以计算出网约车司机接送红码乘客的概率Pi。根据上述方程可以得到，假设网约车司机运送红码乘客后去消毒需要多花费25 min的时间，但可增加收益63元的情况下，车辆接送红码乘客的概率为99%。

3.3 预测检验

当二元离散选择模型被估计后，将所有样本的解释变量观测值代入模型中，通过计算得到每个样本的被解释变量选择1的概率，与每个样本被解释变量的实际观测值进行比较，从而判断模型的预测效果。由于本文的全部样本中选择1和选择0的样本数目相当，因此以0.5为临界值进行预测检验，所得结果如图11所示，可以得到预测车辆接送红码乘客的准确率为87.5%。

4 新冠肺炎疫情背景下的网约车应对策略

目前国内对于疫情的防控已经进入常态化管理阶段，人民生活也逐渐恢复正常，出行需求增加。结合此次疫情的发展趋势，在大运量公共交通暂停运营期间，网约车在保障交通运输体系的稳定畅通中发挥了重要作用，同时非接触式的网约车出行方式对个体的安全出行也起到了积极作用。本文基于对COVID-19病毒的传播过程进行分析后，针对疫情期间网约车的运营管理制定相关的应对策略。

4.1 控制车内人员数量

从SEIR模型的模拟结果来看，接触人数越多，病毒传播感染的概率就越大，因此控制车内人员的数量是十分必要的。在此次疫情中，健康码的出现成为了国内在掌握全民疫情风险信息的一个数字抗疫亮点，考虑到健康码为红色的乘客携带病毒的可能性较高，提出利用车内安装防护膜的网约车接送此类乘客，并且每辆车只能接送一名乘客，在接送完成后还需要对车辆进行消毒。对于健康码为绿色的乘客，每辆车的车内人员数量控制在3名。

4.2 缩短乘客的乘车时间

病毒传播感染的概率与出行者的暴露时间有关，出行者的出行时间越长，感染病毒的可能性越大。因此，针对疫情期间乘坐网约车出行的居民，需要控制相应的暴露时间。为降低出行者的暴露时间，需要减少不必要的绕行距离，减少乘客的候车和乘车时间，降低病毒传播的风险。

4.3 车辆的防疫措施

为防止病毒通过交通运输工具传播扩散，在疫情防控期间要严格按照规范要求，加强对车辆进行消毒消杀工作，并对网约车的车内安全定期进行检查。在车辆内部加装防护膜，将车内司机与乘客进行空间分隔，按时开窗通风与消毒。网约车司机在岗期间要进行体温检测，全程佩戴口罩。乘客通过网约车平台进行车辆预约，在上车前需要出示健康码，乘车期间要全程佩戴口罩。疫情之后相关部门要针对网约车行业制定应急预案，保障交通运输体系的安全运转。

5 结束语

这场突然爆发传染力极强的新型冠状病毒疫情在国家强有力的措施下得到了有效的控制。为了更加清楚地分析新型冠状病毒的传播过程，本文基于SEIR传染病模型对特定情形下疫情的发展趋势进行预测，发现采取控制车内人员数量、缩短乘客乘车时间、对车辆内部进行通风消毒等措施均可有效降低感染率β，当感染率β从0.03降为0.02后，潜伏者和感染者预测趋势图的高峰值明显降低，增长趋势变缓且到达高峰的时间后移;当接触人数r值减少时，潜伏者和感染者的增长趋势变缓，高峰值明显降低。

目前，健康码在人们的出行过程中必不可少，为了降低出行者的风险，本文针对健康码为红色这类风险较高的乘客，提出采取网约车对其进行一对一接送的策略，结果表明这一措施能够有效降低传染风险。由于红码乘客的特殊性，本文利用二元选择模型中的logit模型来预测网约车司机是否接送红码乘客，通过对拟合优度值以及LR统计量的分析，得到检验模型整体显著的结论，意味着收益和时间这两个变量对被解释变量司机是否运输红码乘客具有显著性影响。

参考文献

[1]詹菁， 刘倩， 张雨竹， 等. 新型冠状病毒2019-nCoV的一些初步认识 [J]. 环境化学， 2020， 39（2）： 283-291.

[2]武漢市交通运输局. 4月22日起， 武汉社区应急出租车将有序撤回 [EB/OL].[2020-04-22]. http：//jtj.wuhan.gov.cn/jtzx/zwdt/202004/t20200426_1128159.shtml.

[3]WANG Dong， CAO Wei， LI Jian， et al. DeepSD： Supply-demand prediction for online car-hailing services using Deep Neural Networks[C]// Proceedings of the 2017 IEEE 33rd International Conference on Data Engineering （ICDE）. SAN Diego， CA， USA：IEEE， 2017：243-254 .

[4]高永， 于壮， 邱东岳， 等.  突发疫情期间网约车出行变化分析与对策建议 [J]. 交通与运输2020， 33（S2）： 173-178.

[5]吴楠， 李远东， 赵安琪， 等. COVID-19疫情后武汉市公共交通运营策略研究 [J]. 交通运输工程与信息学报， 2020， 18（3）： 64-73.

[6]张宇， 田万利， 吴忠广， 等. 基于改进SEIR模型的新冠肺炎疫情沿交通线路传播机制 [J]. 交通运输工程学报， 2020， 20（3）： 150-158.

[7]李健， 陈田， 张懿木. 面向传染病疫情防控的公共交通运行管理决策支持研究 [J]. 中国公路学报， 2020， 33（11）： 30-42.

[8]刘海平， 肖尧. 突发疫情防控中公共汽车交通运营管理应对策略 [J]. 城市交通， 2020， 18（3）： 42-45，92.

[9]CHOWELL G， HENGARTNER N W， CASTILLO-CHAVEZ C， et al. The basic reproductive number of Ebola and the effects of public health measures： the cases of Congo and Uganda [J]. Optics Communications， 2004， 229（1）： 119-126.

[10]刘云忠， 宣慧玉， 林国玺. SARS传染病数学建模及预测预防控制机理研究 [J]. 中国工程科学， 2004， 6（9）： 60-65.

[11]FINKENSTADT P. Statistical inference in a stochastic epidemic SEIR model with control intervention： Ebola as a case study [J]. Biometrics， 2006， 62（4）： 1170-1177.

[12]中华预防医学会. 新型冠状病毒肺炎流行病学特征的最新认识 [J]. 中华流行病学杂志， 2020， 41（2）： 139-144.

[13]KAYE P M. Infectious diseases of humans： Dynamics and control [J]. Immunology Today， 1993，14（12）：1-616.

[14]王倩. 滴滴“抗疫”30天 [J]. 商学院， 2020 （Z1）： 112-113.

[15]汪涛， 赵彦云. 基于健康码区块链的新型冠状病毒肺炎疫情防控与评估研究 [J]. 应用数学学报， 2020， 43（2）： 265-277.

[16]聂冲， 贾生华. 离散选择模型的基本原理及其发展演进评介 [J]. 数量经济技术经济研究， 2005 （11）： 151-159.

[17]舒柏晛， 郑丕谔. 基于神经网络的离散选择模型 [J]. 统计与决策， 2005， 19（10S）： 27.

[18]王云泽， 潘兵宏， 邵阳. 互通式立交分流选择行为概率模型研究 [J]. 公路交通科技， 2014， 31（12）： 104-109.

[19]向红艳， 任小聪， 陈坚. 城市群内城际短途出行方式选择行为建模 [J]. 重庆交通大学学报， 2016， 35（3）： 129-133.

[20]杨少伟， 梁汉冕， 潘兵宏. 基于二元Logit模型的驾驶员收费车道选择研究 [J]. 重庆交通大学学报（自然科学版）， 2021， 40（1）： 29-35.

[21]张宁， 戴洁， 张晓军. 基于多项Logit模型的轨道交通站点步行接驳范围 [J]. 城市轨道交通研究， 2012， 15（5）： 46-49.

[22]孙启鹏， 朱磊， 陈波. 基于动态广义费用的客运通道交通方式选擇Logit模型 [J]. 交通运输系统工程与信息， 2013，13 （4）： 15-22.

作者简介： 陈静怡（1997-），女，硕士研究生，主要研究方向：交通运输规划与管理。

收稿日期： 2021-04-09