基于改进RRT算法的移动机器人路径规划

黄文青　陈凌珊　李婷婷　尚大伟

摘 要： RRT算法是一种能够处理障碍物和差分约束的问题的算法，被广泛应用于移动机器人的路径规划。针对于基本RRT算法存在的随机性较大和所求解路径非最优等问题，需要对其进行改进从而优化性能与运行效率。本文主要采用双向RRT算法融合人工势场法的方案进行改进后的路径规划，然后借助Dijkstra算法进一步处理所求解的路径，以寻求路径的最优解。仿真结果表明，本方案可以减少基本RRT算法随机性的影响，提高移动机器人路径规划的效率。

关键词： 移动机器人; 改进RRT算法; 融合人工势场法; 路径规划

文章编号： 2095-2163（2021）07-0032-05中图分类号：TP242文献标志码： A

Mobile robot path planning based on improved RRT algorithm

HUANG Wenqing， CHEN Lingshan，  LI Tingting， SHANG Dawei

（School of Mechanical and Automotive Engineering， Shanghai University of Engineering Science， Shanghai 201620， China）

【Abstract】RRT algorithm is an algorithm that can deal with obstacles and differential constraints， which is widely used in path planning of mobile robots. In view of the large randomness of the basic RRT algorithm and the non-optimal path of the solution， it needs to be improved to optimize performance and operating efficiency. This paper mainly adopts the two-way RRT algorithm fusing artificial potential field method to carry out the improved path planning， and then uses the Dijkstra algorithm to further process the solved path for finding the optimal solution of the path. The simulation results show that this scheme can reduce the influence of the randomness of the basic RRT algorithm and improve the efficiency of mobile robot path planning.

【Key words】mobile robot; improved RRT algorithm; fused artificial potential field method; path planning

0 引 言

随着智能制造行业的快速发展，移动机器人正在发挥着越来越重要作用，人们对其的需求量也在不断增加。在使用过程中，移动机器人需要自主、安全且快速地避开障碍物，并找到到达目标位置的可行路径，因此路径规划问题是移动机器人研究领域中的一个热点[1]。国内外学者针对此问题提出了许多可行的方法，常用的有A*算法、人工势场法、概率路线图（Probability Roadmap Method，PRM）算法、蟻群算法、遗传算法、粒子群优化算法等[2]。

作为一种能解决高维环境下路径规划问题的有效算法，快速搜索随机树（Rapidly Exploring Random Tree，RRT）最早由Lavalle等人提出[3]。相比其它算法，RRT算法的收敛速度较快，能够保证概率完备性[4]。当然，由于随机采样的特点，RRT算法的求解效率比较低。此外，其生成的路径结果比较粗糙，只是一个可行解而并非最优路径[5]。针对RRT算法存在的问题，国内外学者尝试了很多种改进方法。其中，国外比较有代表性的有RRT-Connect算法（Kuffner等人于2000年提出）[6]、RRT*算法（渐进最优）[7]、B-RRT*算法（有选择性地产生新节点）[8]、IB-RRT*算法（在B-RRT*算法的基础上进一步提高搜索速度）[9]和RRT*-Connect算法（使所求解的路径向最优解收敛）[10]等。国内对于RRT算法的研究相对晚一些，王道威等人[11]在2016年提出了动态步长的RRT算法，潘思宇等人[12]在2017年提出了一种引入节点启发式采样函数的RRT*算法，陈波芝等人[13]在2018年提出了用于双机械臂避障的改进RRT算法。

本文采用双向RRT算法融合人工势场法进行改进后的路径规划，再利用Dijkstra算法对所求得的路径再次优化，使得移动机器人能够迅速有效地避开各类障碍物，以提高路径规划的效率。

1 基本RRT算法

1.1 RRT算法的基本思想

对于移动机器人而言，路径规划是指其能够在具有障碍物的较复杂环境中找到一条由起始点qinitial抵达目标点qgoal的路径，且在运动过程中不碰到周围的障碍物[14]，如图1所示。

作为一种常用的路径规划算法，RRT算法是适用于高维空间和复杂约束的问题，这里的约束主要是由障碍物造成的代数约束和由环境变化带来的微分约束。其基本思想是移动机器人在向目标点运动的过程中借助产生的随机点来决定步长，从而避开障碍物。求解时不需要对移动机器人进行系统建模，也无需对搜索区域进行几何划分，搜索的范围较广、覆盖率较高。

1.2 RRT算法的具体过程

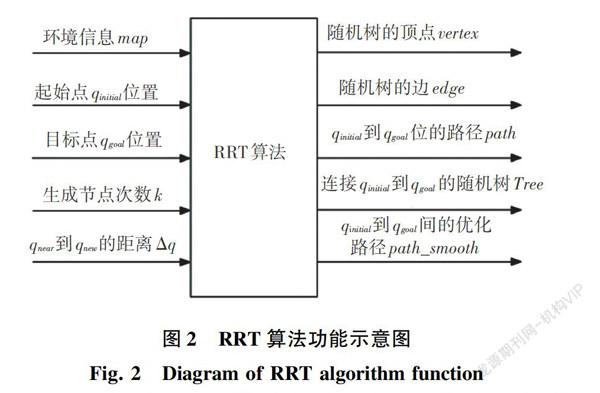
根据RRT算法的基本思想，若要构建RRT算法，必须要先明确算法的输入与输出。RRT算法的输入主要有环境信息、起终点位置、节点的生成次数以及随机点与最近树节点的距离;输出主要有随机树的顶点与边、起终点间的原始路径、生成的连接起终点的随机树以及平滑处理后的优化路径，如图2所示。

总地来说，RRT算法的过程可以分为3部分：插入新的节点、障碍物检测和非完整约束检测。当且仅当这两类检测均满足要求时，才能加入新的节点。其伪代码如下：

其中，rand（ ）的作用是在环境中产生随机点;neighbour（ ）的作用是找出随机树上距离随机点最近的节点;input（ ）的作用是依据随机点和邻近节点的特征扩展随机树;state（ ）的作用是生成新的树节点;judge（ ）和if（ ）主要是进行障碍物检测和约束判断。

2 RRT算法的改进

针对RRT算法在较复杂环境中随机性较大、收敛速度较慢和运行效率较低等问题，本文主要做出如下改进。

2.1 双向RRT算法

基本RRT算法的搜索过程是从起始点qinitial开始生成随机树，从而延伸至整个状态空间。很明显，当状态空间的环境较为复杂时，譬如障碍物较多或者运行路径较狭小时，算法的收敛速度会大幅下降，导致需要花费很长的时间来计算路径，有时甚至得不到结果，如图3所示。

针对上述问题，双向RRT算法能够从目标点qgoal生成随机树，也是进行随机采样并扩展，这就使得对状态空间的搜索效率得到提高。需要提出的是，从目标点qgoal生成的随机树扩展方式是不同的，其倾向于朝起始点qinitial的随机树新节点qnew扩展。在整个路径的搜寻过程中，这两棵随机树能够交替扩展。当qgoal的随机树无法扩展，或者其新节点qnew与qnew重合时，退出算法。此时，由目标点qgoal和起始点qinitial生成的2棵随机树互相连接，一个路径的可行解就得到了，如图4所示。很显然，相对于基本RRT算法的搜索过程，这种双向搜索过程步长更大，随机树的生长速度也更快。这使得双向RRT算法的运算效率更快。

由于目标点qgoal随机树的扩展方式有所不同，且也涉及到障碍物的判断与碰撞检测，这里给出部分伪代码见如下。

2.2 人工势场法的融合

为了进一步提高RRT算法的搜索效率，降低随机性，本文利用人工势场法的目标导向特征来引导随机树向着目标点qgoal扩展，使RRT算法能尽快完成路径规划。

人工势场法最早是Khatib提出的[15]，主要定义了目标点qgoal的引力势场和斥力势场，继而引导移动机器人朝着势场函数负梯度方向运动，从而避免与障碍物碰撞。其中，引力势场函数为：

斥力势场函数为：

相应地，其负梯度分别为：

其中，kp为引力系数;kr为斥力系数;xgoal为目标点qgoal的位置;y为移动机器人与障碍物的距离;y0为障碍物的斥力作用的最大范围。

根据人工势场法的特性，其与双向RRT法融合可以进一步修正RRT算法的随机树扩展方向，提高算法的实时性，避免产生局部极小值，优化移动机器人路径规划的能力。

为此，需要给随机树的节点qnew构造目标引力函数P（qnew）。目标引力函数和随机树的扩展机制共同作用，继而引导节点qnew朝着目标点延伸。因此，qnew的扩展函数可表示为：

其中，T（qnew）为RRT算法的随机扩展函数。

由此构造出的目标引力函数为：

其中，ρ为引力系数。当ρ取不同的值时，随机树向目标点qgoal的导向性是不同的。经过与人工势场法的融合，RRT算法随机点qnew的生成可以通过如下公式进行计算：

2.3 路径处理

由于双向RRT算法仍具有一定的随机性，其与人工势场法融合后还是会有多余的随机点。由于不具有目标点的导向性，这些随机节点并没有意义，需要对其进行删减。为此，本文选择Dijkstra算法处理所求路径结果。

Dijkstra算法是以起始点作中心逐步向外求解到图中（一般为有向图）其余顶点的最短路径，直到抵达目标点。一般来说，Dijkstra算法主要分为3部分，对此拟做阐释分述如下。

（1）初始化起始点、目标点、步长等信息，定义相应数组来所求结果。

（2）循环迭代，依次求解起始点到各顶点之间的最短路径。因为每次求解都涉及一个顶点，所以循环次数比顶点总数少1。

（3）根据结果将相关顶点和距离信息存入对应数组中。

具体来说，连接随机树中的各个节点qinitial、q1、q2、……、qgoal，碰到障碍物就停止，并存储当前节点qt，然后从下一个节点qt+1起再次连接至qgoal，过程中如有障碍物做类似处理。最后，数组{qt}中的每个元素就是处理后的路径上的各节点。

综上所述，整个改进算法的流程如图5所示。

3 仿真试验

本次改进RRT算法试验的仿真平台为Matlab R2017b，环境的空间范围为550 mm*550 mm，各类黑色的几何形状为障碍物。初始化移动机器人设置，起始点qinitial的坐标设为（10，10），目标点qgoal的坐标设为（500，500）。RRT算法的步长设为5，最大循环次数为10 000。

基本RRT算法的搜索过程和生成路径如图6所示，改进算法的搜索过程和生成路径如图7所示。表1记录的是这2种情形下的路径长度和规划所用时间。

由此可见，改进后的算法能够规划出更优化的路径，而且所用时间更短。

4 结束語

本文分析了基本RRT算法的特征，并對其存在的相关问题进行改进。通过双向RRT算法与人工势场法的融合，路径搜索过程的目标导向性更强，路径得到了优化，时间也进一步缩短，具有良好的应用前景。

参考文献

[1]王坤， 曾国辉， 鲁敦科， 等. 基于改进渐进最优的双向快速扩展随机树的移动机器人路径规划算法[J]. 计算机应用， 2019， 39（5）： 1312-1317.

[2]SFEIR J， SAAD M， Saliah-Hassane H： An improved artificial potential field approach to real-time mobile robot path planning in an nnknown environment [C]// IEEE International Symposium on Robotic and Sensors Environments. QC， Canada ：IEEE，2011：208-213.

[3]LAVALLE S M， KUFFNER J J. Randomized kinodynamic planning [C]//Proceedings of the 1999 IEEE International Conference on Robotics and Automation. Piscataway，NJ：IEEE，1999：473-479.

[4]NGUYEN M K， LEONARD J， STEPHANE R. ART-RRT： As-rigid-as-possible exploration of ligand unbinding pathways [J]. Journal of Computational Chemistry， 2018， 39（11）：665-678.

[5]徐秉超， 严华. 一种改进的双向快速搜索随机树算法[J]. 科学技术与工程， 2020， 20（19）： 7765-7771.

[6]KUFFNER J J， LAVALLE S M. RRT-connect： An efficient approach to single-query path planning[C]//Proceedings of the 2000 IEEE International Conference on Robotics and Automation. Piscataway，NJ： IEEE，2000：995-1001.

[7]KARAMAN S， FRAZZOLI E. Sampling-based algorithms for optimal motion plannings [J].The International Journal of Robotics Research， 2011， 30（7）：846-894.

[8]Jordan M， Perez A. Optimal bidirectional rapidly-exploring random trees [R]. Cambridge， MA ：Computer Science and Artificial Intelligence Laboratory， Massachusetts Institute of Technology， 2013.

[9]QURESHI A H， AYAZ Y. Intelligent bidirectional rapidly-exploring random trees for optimal motion planning in complex cluttered environments [J]. Robotics and Autonomous Systems， 2015， 68：1-11.

[10]KLEMM S， OBERLANDER J， HERMANN A， et al. RRT*-Connect： Faster， asymptotically optimal motion planning[C]//2015 IEEE International Conference on Robotics and Biomumetics. Seattle， WA，USA：IEEE， 2015：1670-1677.

[11]王道威， 朱明富， 刘慧. 动态步长的RRT路径规划算法[J]. 计算机技术与发展， 2016（3）： 105-107，112.

[12]潘思宇， 徐向荣. 基于改进RRT*的移动机器人运动规划算法[J]. 山西大学学报（自然科学版）， 2017， 40（2）： 244- 254.

[13]陈波芝， 陆亮， 雷新宇， 等. 基于改进快速扩展随机数算法的双机械臂协同避障规划方法[J]. 中国机械工程， 2018， 29（10）： 1220- 1226.

[14]金丹. 基于改进RRT算法的移动机器人路径规划[J]. 现代计算机， 2018（6）： 41-44.

[15]KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[M]//COX I J， WILFONG G T. Autonomous robot behicles. New York， NY ：Springer，1986：396-404

基金项目： 上海工程技术大学研究生科研创新项目（0231-E3-0903-19-01213）。

作者简介： 黄文青（1996-），男，硕士研究生，主要研究方向：汽车智能化控制和测试。

通讯作者： 黄文青Email：394737977@qq.com

收稿日期： 2020-12-24