一种改进的粒子群优化算法

胡建华　熊伟利

摘 要： 粒子群优化算法（PSO）是一种群体智能进化计算方法，但在搜索过程中粒子紧跟最优粒子运动降低了粒子多样性和全局搜索能力，从而易陷入局部极值。本文提出一种新的粒子群优化算法（PSO-EWD），主要改进体现在2个方面：将惯性权重与进化因子相关联，根据种群的进化状态而改变权重大小，以平衡全局搜索能力与局部搜索能力;将时变的分布式时延引入速度更新公式中，以增加粒子的多样性。本文通过5种算法在9个基准函数上的实验对比，证明了新提出的算法相较于另外4种算法具有更优的适应度值、稳定性和收敛速度。

关键词： 分布式时延; 进化因子; 权重; 粒子群优化

文章编号： 2095-2163（2021）07-0006-07中图分类号：TP301文献标志码： A

An improved Particle Swarm Optimization algorithm

HU Jianhua， XIONG Weili

（College of Science， University of Shanghai for Science and Technology， Shanghai 200093， China）

【Abstract】Particle Swarm Optimization algorithm （PSO） is a kind of evolutionary calculation method with swarm intelligence. In the search process， all particles closely follow the optimal particle's movement， which reduces the particles' diversity and global search ability. So it is easy to fall into local optima. In this paper， a new swarm optimization algorithm （PSO-EWD） has been proposed which is mainly improved in two aspects： the inertia weight is associated with the evolution factor， and the weight is changed according to the evolution state of the population to balance the global search ability and the local search ability; the distributed time-varying delays are introduced into the velocity update formula to increase diversity of the particles. In this paper， the experimental comparison of five algorithms on nine benchmark functions shows that the proposed algorithm has better fitness value， stability and convergence speed than the other four algorithms.

【Key words】distributed time-delay; evolutionary factor; weight; Particle Swarm Optimization （PSO）

0 引 言

粒子群優化算法（PSO）[1]是一种种群随机搜索算法，其灵感来源于鸟类的群集行为。由于PSO算法原理简单、易实现的特点，在众多领域中有着广泛的应用。但PSO算法也有收敛速度慢和容易陷入局部最优等不足。一方面是由于PSO算法对其控制参数相当敏感，合理的参数配置才能提高算法的性能， PSO-LDIW（Shi和Eberhart ，1998年、1999年）[2-4]、PSO-CK（Clerc和Kennedy， 2002年）[5]、PSO-TVAC（Ratnaweera，2004年）[6]等算法应运而生。另一方面，所有粒子紧跟最优粒子运动降低了粒子多样性和全局搜索的能力。经典的PSO算法仅关注于粒子的当前速度、当前位置、个体最优位置和全局最优位置，忽略了粒子的历史信息和种群的分布状态等因素。 2007年，Zhan等人[7]用聚类分析方法，分析了搜索过程中种群分布特性，提出种群进化状态这一概念。2009年，Zhan等人[8]提出了一种自适应PSO算法（APSO），该算法根据种群实时进化状态来实现惯性权重的自动控制，用以提高搜索效率和收敛速度。进一步考虑到历史信息对粒子当前速度的影响，时延这一概念被引入PSO算法中，SPSO（Tang等人，2011年）[9]、SDPSO（Zeng等人， 2016年）[10]、MDPSO（Song等人，2017年）[11]等变体相继被提出来。这些算法有效地平衡了局部搜索和全局搜索能力，提高了粒子的多样性。2019年，Liu等人[12]引入随机分布式时延，提出RODDPSO算法，该算法充分考虑了历史个体最优和全局最优信息，但却忽略了不同阶段的历史信息对当前状态的影响是不同的。

在此基础上，本文综合考虑了种群的进化状态和不同阶段时延的影响效果，提出了一种改进的PSO算法（PSO-EWD）。该次研究的创新点在于：将惯性权重与进化因子相关联，根据种群的进化状态而改变权重大小，使全局搜索能力与局部搜索能力得到平衡;将时变的分布式时延引入速度更新公式中，以增加粒子的多样性。

1 PSO算法

假设S为种群粒子数，I={1，2，3，…，S}， D代表搜索空间的维数，则第i个粒子的速度用Vi表示，位置用Xi表示，其中Xi，Vi∈RD， i∈I。設第k次迭代后第i个粒子的速度为Vi（k）=（Vi1（k），Vi2（k）， …，ViD（k））位置为Xi（k）=（Xi1（k）， Xi2（k），…，XiD（k））。原始的PSO算法在寻找最优解的过程中所有粒子都紧跟个体最优粒子和全局最优粒子，向着全局最优位置移动，记第i个粒子的最优位置为Pi=（Pi1，Pi2，…，PiD），全局最优粒子的位置为PG=（PG1，PG2，…，PGD。更新迭代公式是：

其中，k是当前迭代次数;ri（i=1，2）是D维向量，向量中每一个分量都是[0，1]上的随机数;ω为惯性权重;c1是个体认知加速度系数;c2是社会加速度系数。

其中，ωmax（ωmin）表示在寻优过程中惯性权重的最大（最小）值; iter（max iter）表示当前（最大）的迭代次数。

2002年，Clerc和Kennedy指出当ω=0.729， c1=c2=1.49时算法效果较好[13]（PSO-CK算法）。2004年，受时变惯性权重的启发， Ratnaweera等人提出了PSO-TVAC 算法[14]，将加速度因子改进为：

其中，c1i（c1f）和c2i（c2f）分别是个体认知加速度系数和社会加速度系数的初值（终值），这些参数的取值为：c1i=2.5， c1f=0.5， c2i=0.5， c2f=2.5。

2 改进的PSO算法

2.1 进化状态的判断

2009年，Zhan等人[8]通过分析种群的搜索行为和分布特性提出了进化状态，整个搜索过程种群表现出4种状态：收敛状态、开发状态、勘探状态和跳出状态，分别用ξ=1，2，3，4表示。用di表示第i个粒子与其他所有粒子的平均距离，即：

记dmin， dmax是集合{di|i∈I}中的最小值和最大值，用G表示全局最优粒子，显然dmin≤dG≤dmax。令：

称为种群的进化因子，式（6）表明进化因子能恰当刻画种群的分布状态，根据进化因子Ef的大小不同而取不同状态[9]：

2.2 新算法的构建

经典的PSO算法开始搜索时速度很快，但在搜索过程中，所有的粒子都向着当前最优粒子的方向寻找，这使粒子失去了多样性，在搜索后期收敛速度明显下降，并且容易陷入局部最优。本文通过考虑不同阶段的历史信息对现在的影响，引入具有时变性的分布式时延，以增加粒子的多样性;同时将惯性权重与进化因子相关联，来平衡算法的全局搜索和局部搜索的能力。改进后的PSO-EWD算法的迭代公式为：

其中，ω（Ef）是和进化因子Ef相关的惯性权重，r3，r4是如同r1，r2的D维随机向量;α（τ）为随机数0或者1;ω1是时延发生时的自适应权重，决定了每个时延影响的大小; ∑Nτ=1ω1α（τ）（Pi（k-τ）-Xi（k））， ∑Nτ=1ω1α（τ）（PG（k-τ）-Xi（k））分别是关于自我认知和社会的分布式时延项，这里的τ是时延步数，N为分布式时延步数最大值; 约定当τ≥k时，Pi（k-τ）=Pi（k）， PG（k-τ）=PG（k）; ξ（k）是第k次迭代时种群的当前的状态;c3和c4是分布式时延项的加速度因子;ml（ξ（k））和mG（ξ（k））是分布式时延项的强度因子，两者都是根据进化状态ξ（k）所确定的。

2.3 参数

惯性权重ω用来平衡算法的全局搜索能力和局部搜索能力，PSO-EWD算法将ω与进化因子Ef相联系，以适应于搜索环境。因为相对较小的ω有利于种群收敛和开发，相对较大的ω有利于种群勘探和跳出，而进化因子在跳出状态时相对较大而收敛状态时相对较小，本文取ω（Ef）的初值为0.9，计算公式为：

权重ω1用来控制时延项对速度的影响， 因为离当前状态越近的历史信息对当前状态的影响较大，而越远的历史信息对当前状态的影响相对较小，因此ω1为关于τ的递减函数，本文取：

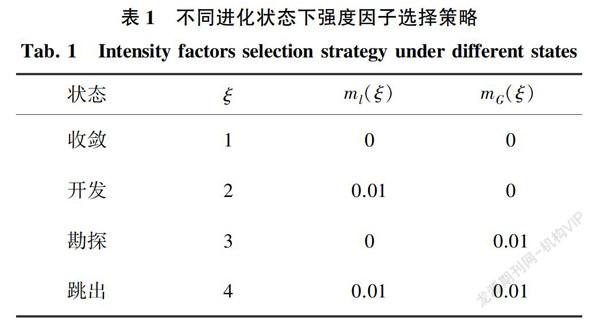
取分布式时延项的加速度因子c3=c1， c4=c2;强度因子ml（ξ）、mG（ξ）根据进化状态ξ 来确定（见表1），其初始值ml（ξ）、mG（ξ）都取为0，在k次迭代后，若种群的进化状态为收敛时，粒子将紧跟当前找到的全局最优粒子快速聚集，忽略时延项的影响而取ml（1）=mG（1）=0;在开发状态时，粒子将利用个体最优历史信息在潜在区域仔细搜索，而忽略全局最优信息的影响，取ml（2）=-0.01， mG（2）=0。在勘探状态时，探索全局最优解是重要任务，鼓励粒子在全局历史最优信息的指导下探索整个搜索空间，取ml（3）=0， mG（3）=0.01;在跳出状态时，粒子群将跟随全局最优粒子飞离局部极值周围区域，去寻求一个更好的解，个体和全局的历史最优位置都需要综合考虑，取ml（4）=0.01， mG（4）=0.01。

3 仿真实验

3.1 基准函数

本文选取9个常见的基准函数来验证算法的性能，其中包括单峰函数、多峰函数。研究中选择的函数、名字、搜索空间等具体信息见表2。

3.2 参数N的训练

在搜索空间随机选取20个种群，所有粒子均具有随机的初始速度Vi（i∈I）和位置Xi（i∈I），计算出每个粒子的适应度值，选出初始个体最优粒子位置Pi和全局最优粒子位置PG。为验证PSO-EWD算法在处理复杂问题时的优越性，本文选定搜索空间的维数为100维，最大迭代次数为20 000次，同时为消除随机因素的影响，每个实验重复40次，最后取平均值。

在PSO-EWD算法的速度更新公式中，分布式时延步数的最大值N是个训练参数，由实验训练所确定。过大的N会增加计算负担，过小的N不能充分发挥时延的作用，本文将在75、100、125、150、175五个数中选取一个使PSO-EWD算法性能较好的N。实验结果如图1所示，纵坐标表示平均适应度值的对数，横坐标表示迭代次数。

由圖1可看出，在5个不同N的取值中，当N=125时函数f2（x），f3（x），f4（x），f6（x）以及f7（x）有最优的适应度值和相对快的收敛速度;虽然函数f1（x），f5（x），f8（x），f9（x）没有最优适应度值，但有更早的收敛趋势。因此本文选取最大时延步数N=125。

3.3 5种算法的对比

本文选取PSO-CK、PSO-LDIW、MDPSO、RODDPSO四种算法来对比验证PSO-EWD算法的优越性。仿真实验结果如图2所示。图2表现了5种算法在100维搜索空间中的收敛性能，对于9个基准函数来说，PSO-EWD算法以更快速度收敛于最优的适应度值。5种算法在100D的搜索空间中的性能比较见表3。由表3可知，从最小值、均值、方差三个评价指标来对比5种算法。从表3中可以看出，PSO-EWD算法在9个基准函数上都有最小的适应度均值，这说明PSO-EWD算法有较好的寻优质量和收敛精度。从方差来看，PSO-EWD算法仅在f5（x）上次于RODDPSO算法，这说明PSO-EWD算法具有较好的稳定性。就最小值而言，PSO-EWD算法仅在f6（x）、f7（x）上次于RODDPSO算法，这说明PSO-EWD有较好的跳出局部极值、寻找全局最优解的能力。进一步仔细比较，算法性能表现次优的是RODDPSO算法，这说明引入了分布式时延的2种算法由于充分考虑了历史个体最优信息和全局最优信息而更能增加粒子的多样性，增强跳出局部最优的能力。而采用与进化状态关联的惯性权重和具有时变性的时延的PSO-EWD算法更能平衡全局搜索能力和局部搜索能力，从而提升了收敛精度。

4 结束语

本文考虑到所有粒子紧跟最优粒子运动降低了粒子多样性和全局搜索能力，提出了一种新的分布式权重粒子群优化算法（PSO-EWD）。通过考虑不同阶段的历史信息对当前速度的影响，引入具有时变性的分布式时延，以增加粒子的多样性;同时，将惯性权重与进化因子相关联，来平衡算法的全局搜索和局部搜索的能力。实验在100维的搜索空间中迭代20 000次，并且为了减少随机因素的影响实验重复40次而取平均值。新算法在9个基准函数上与4种经典的PSO算法对比，实验结果证明PSO-EWD算法具有更优的稳定性、收敛速度与适应度值。

参考文献

[1]EBERHART R， KENNEDY J. A new optimizer using particle swarm theory [C]//Proceedings of the 6th International Symposium on Micro Machine and Human Science.Nagoya， Japan：IEEE， 1995： 39-43.

[2]SHI Y， EBERHART R C. Parameter selection in particle swarm optimization [C]//Proceedings of the 7th International. Conference on Evolutionary Programming. San Diego， CA， USA：IEEE， 1998： 591-600.

[3]SHI Y， EBERHART R C. A modified particle swarm optimizer [C]//Proceedings of IEEE International Conference on Evolutionary Computation. Anchorage， AK：IEEE， 1998： 69-73.

[4]SHI Yuhui， EBERHART R C. Empirical study of particle swarm optimization [C]// Proceedings of the 1999 Congress on Evolutionary Computation.Washington DC， USA：IEEE， 1999， 3：1945-1950.

[5]CLERC M， KENNEDY J. The particle swarm：Explosion，stability，and convergence in a multidimensional complex space [J].IEEE Transactions on Evolutionary Computation， 2002， 6（1）： 58-73.

[6]RATNAWEERA A， HALAAMUGE S， WATSON H C. Self organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients [J]. IEEE Transactions on Evolutionary Computation， 2004，8（3）： 240-255.

[7]ZHAN Zhihui， XIAO Jing， ZHANG Jun， et al. Adaptive control of acceleration coefficients for particle swarm optimization based on clustering analysis [C]//2007 IEEE Congress on Evolutionary Computation. Singapore：IEEE， 2007：3276-3282.

[8]ZHAN Zhihui， ZHANG Jun， LI Yun， et al. Adaptive particle swarm optimization [J]. IEEE Transactions on systems， Man， and Cybernetics，Part B（Cybernetics）， 2009， 39（6）： 1362-1381.

[9]TANG Y， WANG Z， FANG J. Parameters identification of unknow delayed genetic regulatory networks by a switching particle swarm optimization algorithm [J]. Expert Systems with Applications， 2011， 38（3）： 2523-2535.

[10]ZENG Nianyin， WANG Zidong， ZHANG Hong， et al. A novel switching delayed PSO algorithm for estimating unknown parameters of lateral flow immunoassay [J]. Cognitive Computation， 2016， 8（2）： 143-152.

[11]SONG Baoye， WANG Zidong， ZOU Lei. On global smooth path planning for mobile robots using a novel multimodal delayed PSO algorithm [J]. Cognitive Computation，2017， 9（1）： 5-17.

[12]LIU Weibo， WANG Zidong， LIU Xiaohui. A novel particle swarm optimization approach for patient clustering from emergency departments [J]. IEEE Transactions on Evolutionary Computation， 2019， 23（4）： 632-644.

[13]CLERK M， KENNEDY J.The particle swarm：explosion，stability，and convergence in a multidimensional complex space [J]. IEEE Transactions on Evolutionary Computation， 2002， 6（1）： 58-73.

[14]RATNAWEERA A， HALAAMUGE S， WATSON HC. Self organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients [J]. IEEE Transactions on Evolutionary Computation， 2004，8（3）： 240-255.

作者簡介： 胡建华（1978-），女，博士，讲师，主要研究方向：大数据;  熊伟利（1994-），女，硕士研究生，主要研究方向：大数据。

收稿日期： 2021-03-08