雪崩光电器件过剩噪声分析
张 冰,郭雪凯,胡从振,辛有泽,于善哲,雷述宇
(1.西安交通大学微电子学院,陕西 西安 710049;2.宁波飞芯电子科技有限公司,浙江 宁波 315000;3.北京大学微纳加工国家重点实验室,北京 100871)
1 引 言
雪崩光电器件因带宽大、灵敏度高的优点广泛应用于高速光通信网络和低光功率探测领域。依据器件工作模式的差异,雪崩器件又分为雪崩二级管器件(APD)和单光子雪崩二级管器件(SPAD)[1]。雪崩倍增的同时,因电子空穴的碰撞离化过程,会引入过剩噪声,常采用过剩噪声因子F[2]作为评价过剩噪声的性能参数。针对过剩噪声的研究,前人的成果[3-5]表明:过剩噪声因子与触发雪崩的载流子类型(电子触发或空穴触发)、器件的雪崩倍增因子M和离化率比值k有关。此类文章在分析过剩噪声因子时,仅仅聚焦于光子吸收发生在中性体区(N型中性体区或P型中性体区)情况下的过剩噪声,即单独考虑电子注入或者空穴注入下的过剩噪声因子,忽略了耗尽区内的光吸收情况。也有些学者在文章中[6]提到:光吸收发生在雪崩区域内时,因经历的高电场区域变小,碰撞路径变短等因素,雪崩增益会降低,使得增益的波动变大,导致过剩噪声增加。此类文章虽提及了耗尽区内的光吸收,但并未给出耗尽区内过剩噪声因子的分布模型。
无论是雪崩增益还是过剩噪声因子,载流子的碰撞行为是分析和推导模型的基础。载流子在电场驱使下发生碰撞,遵循Branch process[7]过程,运动随机距离后,获得足够的能量与晶格发生碰撞。当碰撞发生时,获得新的载流子。新载流子作为新的分支,继续重复相似的过程。随机的运动距离,即产生随机的离化系数、随机的增益,有随机性就有噪声。前人已经针对雪崩碰撞、离化系数、增益、噪声做了大量研究。Chynoweth[8]分析了Si材料的电子/空穴离化系数,指出离化系数与电场的指数依赖关系,并给出了Si材料中电子的离化系数大于空穴离化系数的结论。Ridley[9]提出了碰撞离化的Lucky-drift机制,揭开了碰撞随机性的神秘面纱。Mcintyre[3]首次分析了均匀电场下,电子注入或空穴注入时的过剩噪声因子,并给出了详细的推导模型,并在他后续的文章中[10]采用统计模型分析了雪崩增益的概率分布。Vanvlite[11-12]采用统计过程阐述了一种载流子触发雪崩和两种载流子触发雪崩的增益和噪声理论。D.S.Ong[13]则使用简单的RPL(randomly-generated ionization path length)模型,由碰撞自由程的随机性角度解释了过剩噪声的起因。Pilicer[14]采用蒙卡仿真和实验验证,提出光吸收深度对过剩噪声因子的影响。Ress[15]和Jamil[16]则在RPL模型的基础上,考虑了碰撞能量的阈值问题,增加了dead space参数,优化了碰撞离化过程和过剩噪声因子。Tarik Baldawi[17]采用N+P结构的器件,分析了PN结的结深、器件材料、触发载流子类型对过剩噪声的影响。无论是模型还是理论分析,前人的工作大部分都聚焦在电场、触发载流子类型对过剩噪声水平的影响,少量的文献提到了光吸收位置的差异引起的额外波动,但并未有详细的模型和分布趋势。
本文从雪崩碰撞的基础理论出发,分析了不同光吸收位置的碰撞行为和过剩噪声。根据不同光吸收位置的雪崩触发差异,将器件的光吸收区细分为三个部分:N型中性体区、P型中性体区、耗尽区,分别讨论光生载流子以不同位置进入耗尽区时的碰撞离化行为和过剩噪声,并重点对光吸收发生在耗尽区时的模型进行分析和推导,结合TCAD和Matlab仿真,对推导模型进行了拟合和验证,其模型计算值很好的符合蒙卡仿真的结果。
2 雪崩增益及过剩噪声分析

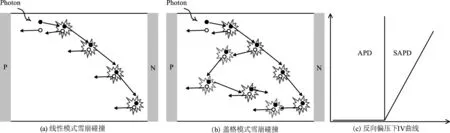
图1 PN结雪崩碰撞和IV曲线Fig.1 Avalanche collision in the PN junction
PN结的雪崩特性提供的高增益使得它被广泛应用于低光子探测和光通信领域,但信号被放大的同时,噪声也经历倍增,且因碰撞离化的随机性又引入了新的噪声,即过剩噪声。

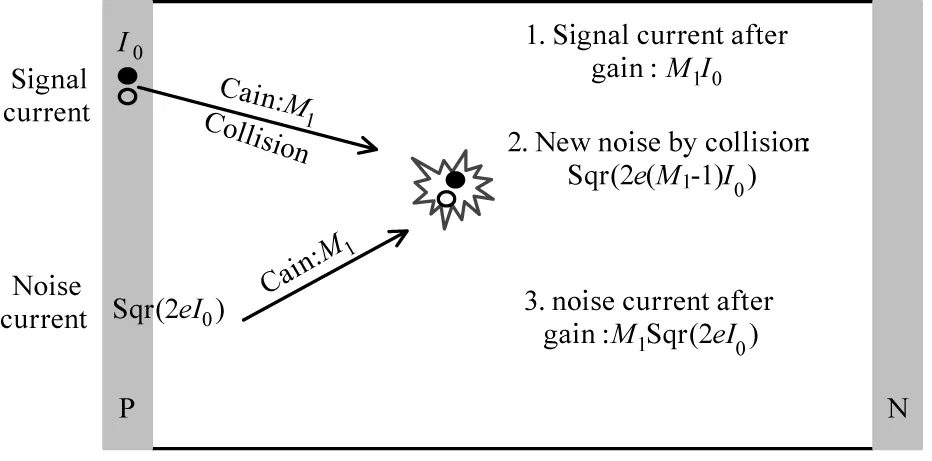
图2 过剩噪声引入过程Fig.2 The process of the excess noise introduce
3 模型推导
前节提到自由程的概率性最终导致PN结中任意位置的增益M(x)是在均值基础上随机波动的,因此电子空穴的每一次碰撞离化,新增的电流因增益的随机性,也会在均值水平上下浮动,其功率谱密度dφ=2edIp(x)df[18]。由M(x)及a、β表达式可知,增益与耗尽区宽度w及耗尽区电场相关。
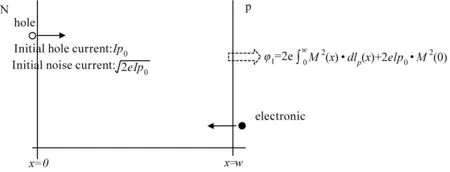
图3 空穴触发雪崩Fig.3 Avalanche triggered by hole

(1)
表达式第一项表示x位置因碰撞新增的噪声电流经雪崩放大后产生的噪声功率谱,第二项表示初始噪声电流雪崩增益后的噪声功率谱。相似的,若光电转换发生在P型中性体区的任意位置时,雪崩倍增后的噪声功率谱密度:
(2)
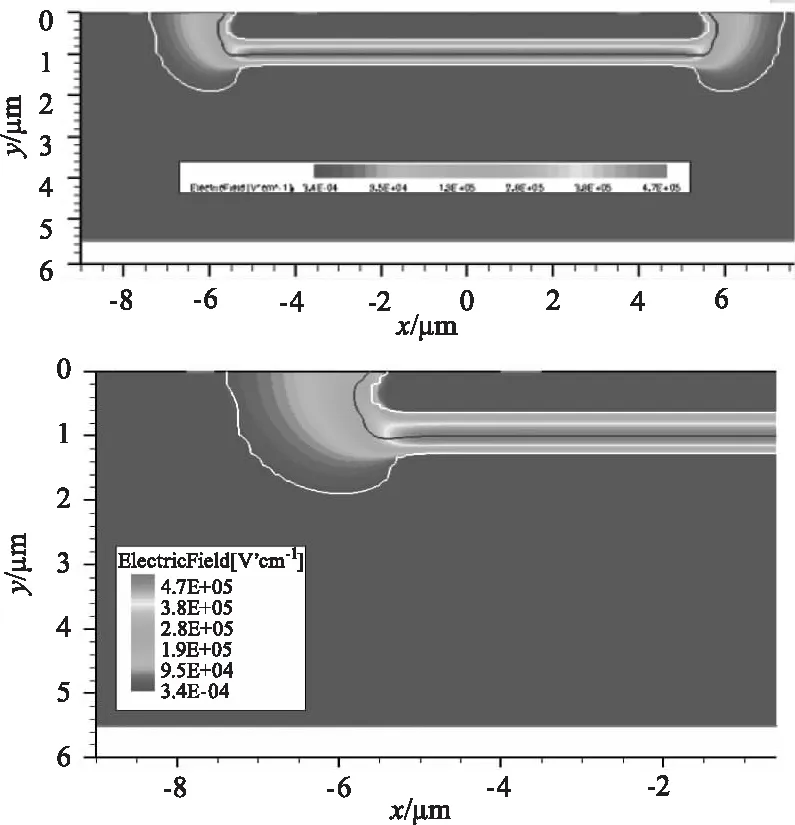
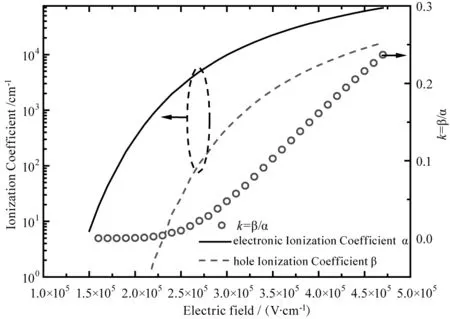
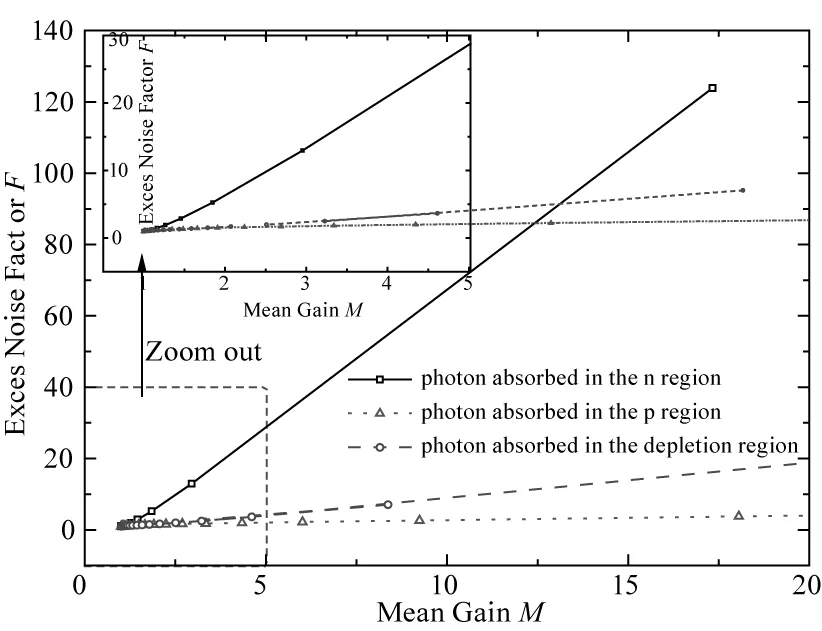
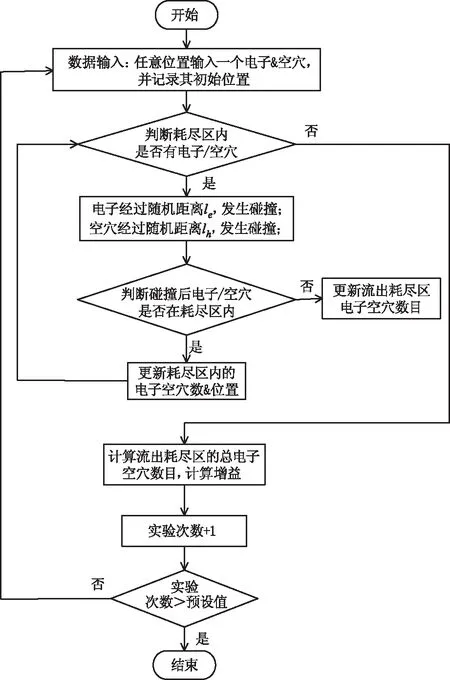
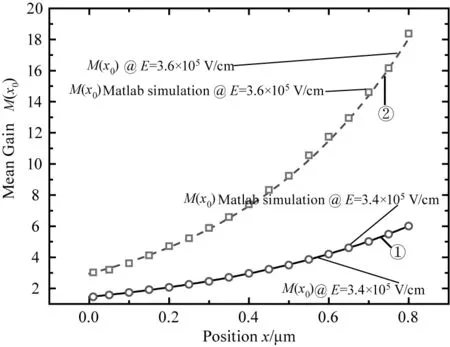
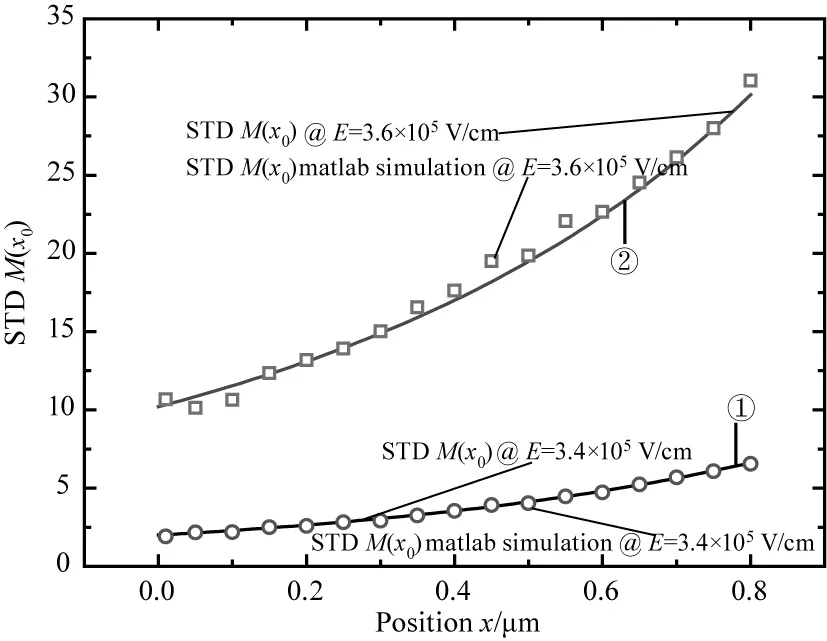
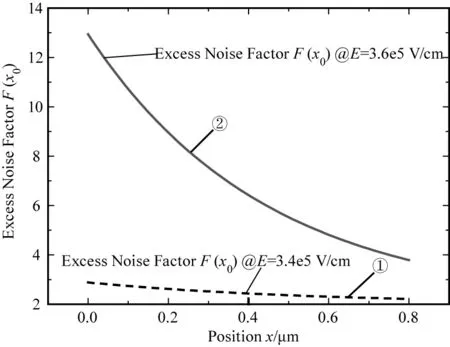
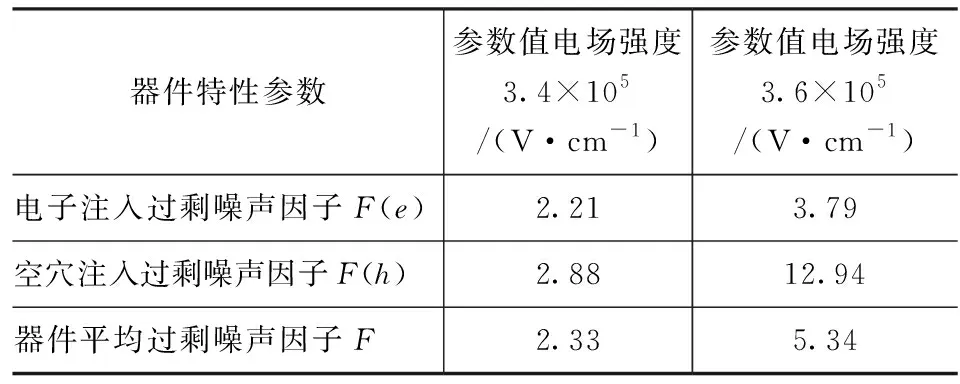
若光电转换发生在耗尽区内任意位置时(0 +2eIP0·M2(x0) (3) 此处的x0表示光电转换发生在耗尽区内的任意x0位置,φ(x0)表示x0位置发生光电转化雪崩倍增后的过剩噪声功率谱。 则增益的波动var(M(x0))可表达为: (4) 同时根据文献[19]的研究结果,可以推导出在耗尽区内任意x0位置发生光电转换时,器件的过剩噪声因子F(x0): (5) 采用TCAD 仿真软件对有源区直径11 μm、外延层厚度5.5 μm的N+P结构的Si-APD器件进行结构建立和特性仿真,电场分布如图4所示,图中给出了单光子雪崩二极管在反向偏置电压为22 V时(击穿电压21 V),器件内部的电场分布情况。从图中可以看出,强电场区域主要分布在PN结区域,颜色越深电场越大,其耗尽区宽度约0.8 μm。根据仿真结果,提取出不同电场强度下的电子离化率a和空穴离化率β及其比值,其依赖关系如图5所示,随着电场增强离化率比值k逐渐增大,空穴的碰撞反馈效应在雪崩增益中的作用逐渐显现,器件工作模式逐渐由线性模式趋近盖格模式。结合TCAD仿真结果和前节推导出的公式,即可计算出均匀电场下,耗尽区内任意光吸收位置x0处的增益M(x0)、增益的波动var(M(x0))及过剩噪声因子F(x0)。图6描述了不同光吸收位置时,不同增益下的过剩噪声因子:从图中可见,过剩噪声与平均增益正相关增长。且相同的增益下,光吸收发生在P中性体区、耗尽区、N中性体区,其过剩噪声因子依次增大,且光吸收发生在耗尽区内的过剩噪声因子更偏向P中性体区光吸收时的过剩噪声因子。因此可以通过合理优化器件结构,使更多的光被吸收在P中性体区,可有效减小过剩噪声。 图4 TCAD 仿真电场分布Fig.4 TCAD simulation for electric field distribution 图5 不同电场下电子离化率a、空穴离化率β及其比值kFig.5 Lonization coefficient for electronic and hole and the rate k under different electric field 为验证推导结论,采用matlab仿真模拟电子空穴在耗尽区的碰撞行为。仿真用的蒙卡模型主要是随机碰撞长度(RPL)模型,引入一个随机长度l作为电子或空穴的平均自由程,该随机长度满足指数分布,由程序产生的随机数通过公式计算可得。程序开始时,位置x=x0注入电子,电子在电场作用下向x=0方向运动,经过随机长度le(由计算机产生的0到1之间的随机数r和公式le=de-logr/α,计算出来,α表示电子的电离系数,de为死区时间,即电子不会发生离化的加速距离)发生第一次碰撞,产生新的电子-空穴对,记录此时新的电子位置position_e[]和空穴位置position-h[],并判断电子和空穴是否已经流出PN结耗尽区。 图6 不同光吸收位置,不同增益下的过剩噪声因子趋势图Fig.6 Excess noise factor under different mean gain when photon is absorbed in the N type and P type neutral region 若流出耗尽区,则电子和空穴的数量+1,若未流出耗尽区,电子和空穴继续运动经过随机长度le或lh发生下碰撞,直到所有碰撞的电子数和空穴都流出PN结,记录总的电子数和空穴数,计算雪崩增益。程序进行300000次,因随机数l不确定性,在耗尽区内的总的碰撞次数也是不定的,最终产生的增益也在均值上下波动,记录每次的增益,最后求出平均增益及其标准差,程序流程如图7所示。 图7 Matlab仿真程序流程图Fig.7 Matlab simulation flow chart 图8为耗尽区内,不同光吸收位置的增益计算值M(x0)和Matlab仿真值对比。为体现模型的可靠性,所有的拟合验证工作均采用线性模式下的2个不同电场强度作为器件工作条件:3.4×105V/cm电场强度时,增益较小;3.6×105V/cm电场强度,器件接近击穿,增益较大。如图8,线①为电场强度为3.4×105V/cm时,耗尽区内不同位置的增益M(x0),圆(○)为同等电场强度下的Matlab仿真值;线②为电场强度为3.6×105V/cm时,耗尽区内不同位置的增益M(x0),空穴方块(□)为同等电场强度下的Matlab仿真值。对比结果来看,M(x0)理论计算值能很好的符合Matlab仿真结果。 图8 不同光吸收位置的增益M(x0)的模型计算值和Matlab仿真值Fig.8 Model value and matlab simulation value for mean gain M(x0) under different photon absorption locations 图9为不同光吸收位置的增益的波动计算值var(M(x0))和Matlab仿真值对比。线①为电场强度为3.4×105V/cm时,耗尽区内不同位置的增益波动var(M(x0)),空心圆(○)为同等电场强度下的Matlab仿真值;线②为电场强度为3.6×105V/cm时,耗尽区内不同位置的增益波动var(M(x0)),空穴方块(□)为同等电场强度下的Matlab仿真值。对比结果来看,var(M(x0))理论计算值能很好的符合Matlab仿真结果。图10为不同电场,耗尽区内不同光吸收位置的过剩噪声因子,线①表示电场为3.4×105V/cm时,耗尽区不同光吸收位置的过剩噪声因子F(x0);线②表示电场为3.6×105V/cm时,耗尽区不同光吸收位置的过剩噪声因子F(x0)。 图9 不同光吸收位置的增益的波动计算值var(M(x0))和Matlab仿真值Fig.9 Model value and matlab simulation value for gain various var (M(x0))under different photon absorption locations 图9中可见,光电转换位置越靠近N中性体区,过剩噪声因子越大,主要因为靠近N中性体区时,空穴向P中性体区方向运动的碰撞路径增大,由空穴触发雪崩占主导,因此过剩噪声增大。考虑光子在器件不同位置的吸收率差异,器件的平均过剩噪声因子: (6) 其中,(0,w1)为N型中性体区范围;(w1,w2)为耗尽区范围;(w2,∞)为P型中性体区范围,在计算仿真时,N中性体区宽度为0.6 μm,耗尽区宽度为0.8 μm,P中心体区范围为4.1 μm。a为光吸收系数,这里采用的是940波长的光在Si材料的吸收系数,174.61 cm-1。 图10 耗尽区内不同光吸收位置的过剩噪声因子Fig.10 Excess noise factor in the different location of depletion region 表1为根据仿真提取的离化率参数,计算出的器件噪声因子。F(e)为只考虑电子在P型中性体区吸收时的过剩噪声因子,F(h)为只考虑空穴在N型中性体区吸收时的过剩噪声因子,F为考虑光子在器件内不同位置的吸收比例计算的平均过剩噪声因子。 表1 器件过剩噪声因子Tab.1 Excess noise factor parameters for device 文章基于雪崩碰撞理论,分析不同光吸收位置,PN结的雪崩碰撞行为及其引起的过剩噪声,并进行公式推导。同时采用TCAD仿真提取电场、离化率参数,进行不同光吸收位置的增益M(x0)、增益波动var(M(x0))、过剩噪声因子F(x0)的计算,最后采用Matlab的蒙卡仿真验证推导公式,其结果证明,推导出得增益模型和Matlab仿真结果具有很好得拟合度。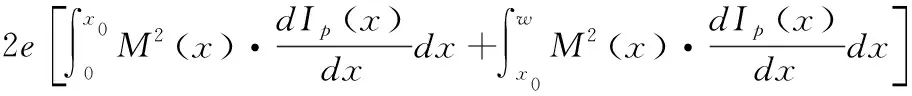
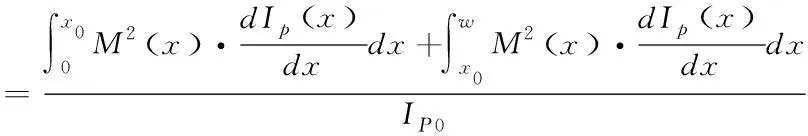
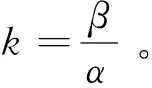
4 仿真结果及验证

5 结 论

