对电流模式控制Buck-Boost 变换器的混沌控制研究

王浩宇，董学育，朱建忠

（南京工程学院电力工程学院，江苏南京 211167）

直流开关变换器是一种能将直流电能转换成负载所需的直流电能的电力电子装置，因其可靠性好、工作频率较高目前被广泛应用于各种发电系统如光伏、风力发电系统，以及直流微电网结构中的直流储能、直流负荷装置[1-2]等场景，根据电路接线方式直流变换器主要有4种类型，而其中的降升压(Buck-Boost)变换器由于既可以升压又能降压的特点相比之下更具研究价值；但直流开关变换器作为一种强非线性系统，在受到光照强度、温度、风力等外界条件影响时其输入电压、参考电流等工作参数会发生变化，从而导致器件会发生一系列如分岔、混沌等非线性现象[3-12]，使得变换器功率发生波动、输出电压电流不稳定甚至无法正常工作等不利后果，因此对Buck-Boost变换器非线性行为的研究分析，并通过合理的混沌控制策略使变换器由不稳定的混沌态重新回到稳定运行的周期状态，对于直流开关变换器未来的应用发展具有指导意义，对于直流微网的稳定运行也具有重要意义。

1 Buck-Boost变换器建模

该研究主要对象是电流模式控制的Buck-Boost变换器，利用电感电流iL作为控制对象进行仿真分析，具体电路工作原理如图1 所示。

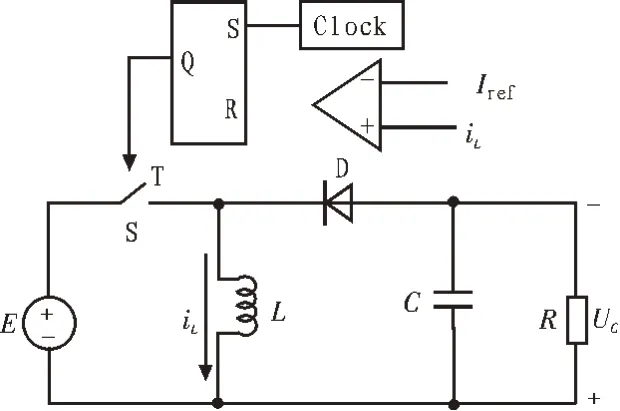
图1 电流模式控制的Buck-Boost变换器原理

考虑变换器的电感电流iL处于连续状态即CCM模式[8]下，根据开关管S 以及二极管D 的通断，直流变换器在一个周期T内包含两种工作模态：1）时钟脉冲发出信号后，开关管S 被切换导通，此时电感电流iL处于上升状态；2）当电感电流iL上升至参考电流Iref的大小时，触发器复位切换开关管S 关断，负载所需要的电能由电感和电容提供，iL下降直至下个周期信号到来。

根据该原理图可得变换器状态方程为：

式中，x=[iL,UC]T，电感L的电流iL以及电容C上的电压UC是微分方程的状态变量，E为直流输入电压，

根据控制开关管S 通断的信号值u的不同，将式（1）两个方程合并可以得到Buck-Boost 变换器的分段线性模型为:

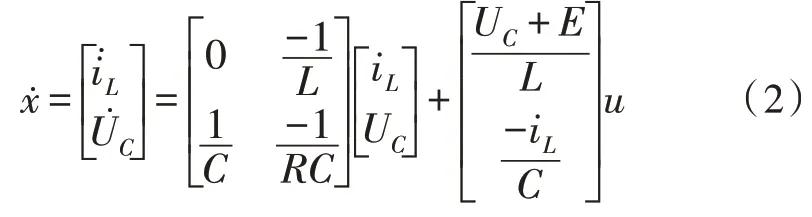
式中，u=1，表示开关S 闭合，u=0 则表示开关断开；根据式（1）在Simulink 环境下搭建了Buck-Boost变换器仿真模型，如图2 所示。

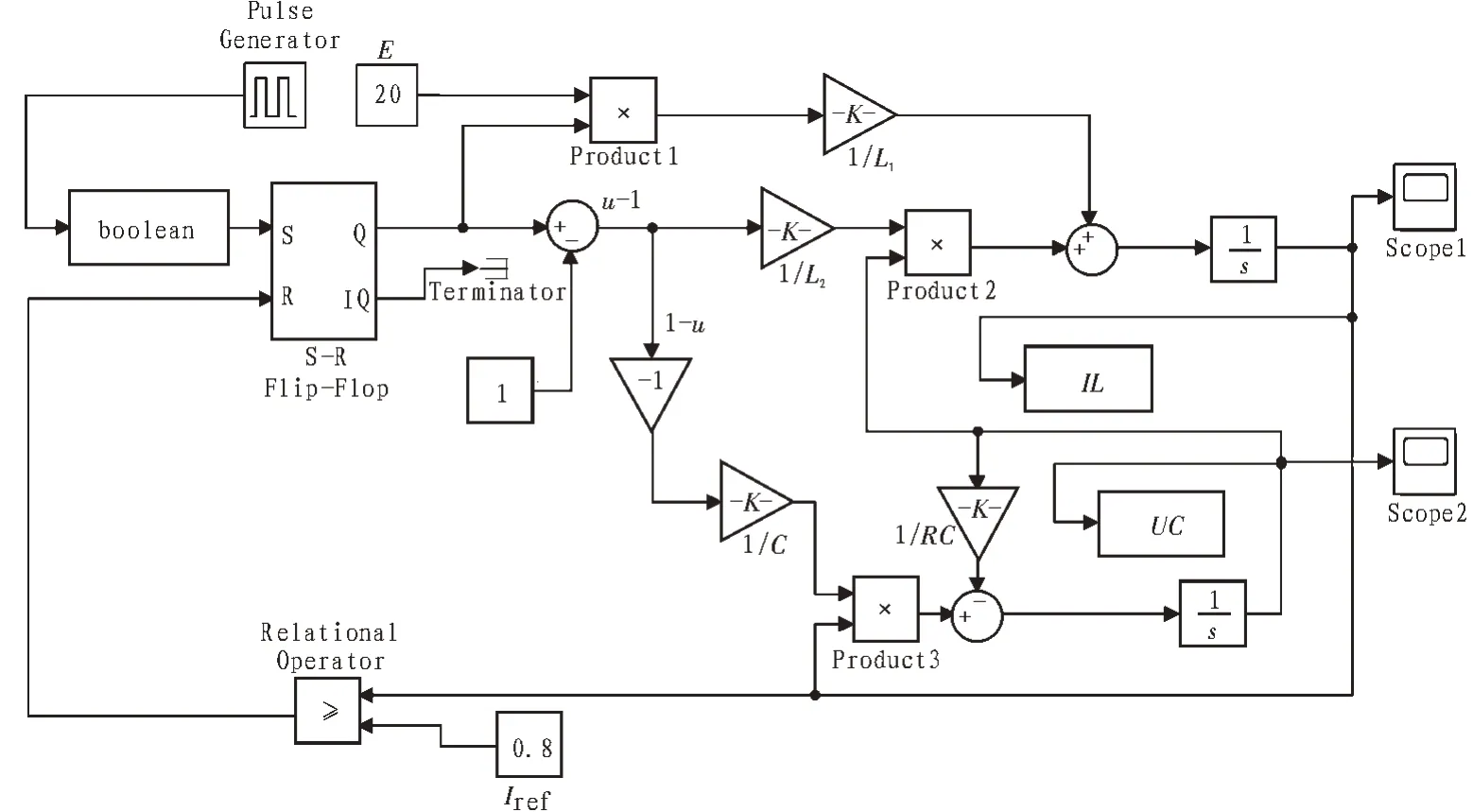
图2 电流模式控制Buck-Boost变换器仿真模型

在该模型中，时钟信号由时钟脉冲发生器模块（Pulse Generator）提供，幅值为1，周期T=50 μs；同时使用Realtional Operator 模块给触发器的R 端提供逻辑值0 或1；此外为保持数据类型一致，需在RS 触发器前加Boolean 模块，该模块作用是将脉冲信号转化为逻辑量，将原为零的数置为0，原为非零的数置为1，以此给RS 触发器的S 端提供逻辑值；其余如电感量、电容量均以增益模块Gain 表示，输入电压用常数模块Constant 表示；在仿真参数设置中，仿真运行时间设为0.01 s，选择变步长模式，解法器选择ode23。

2 混沌态分析

在搭建了上节所示的变换器仿真模型后，可以通过调整电路参数分析Buck-Boost 变换器的非线性行为变化，以输入电压E作为变化参数，范围为10～50 V，在仿真过程中每次将E以1 V 的大小逐步调整，观察Buck-Boost 变换器的运行状态，对其余电路参数进行以下设置：时钟周期T=50 μs，电感L=0.5 mH，电容C=4 μF，电阻R=20 Ω，参考电流Iref=4 A，仿真时间设为0.01 s。

仿真结果如图3～4 所示，当输入电压E为15 V时，变换器已进入不稳定的混沌态，图3 是输出电压Uc的时域波形图，图4 是输出电压UC与电感电流iL构成的相轨迹图[13-16]。

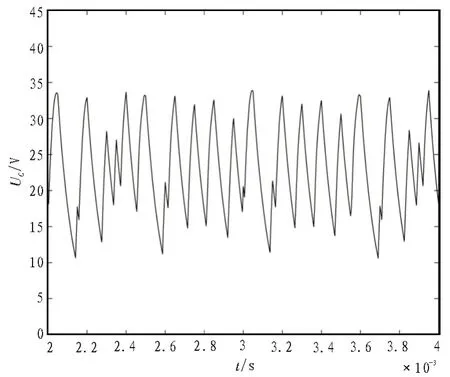
图3 输出电压UC的时域波形图

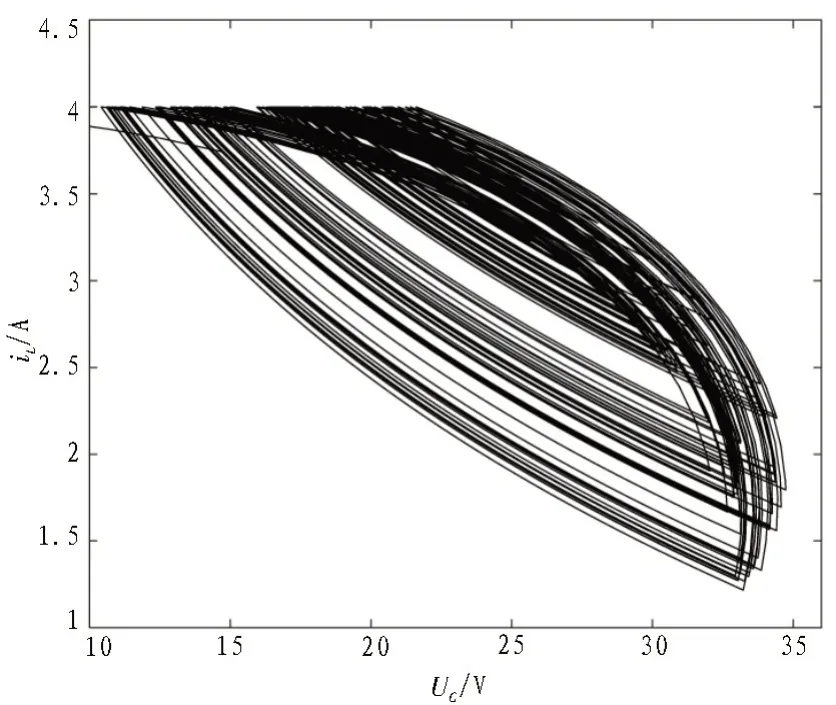
图4 E=15 V时的相轨迹图

图3 表明当Buck-Boost 变换器进入混沌态后，其输出电压UC的波形不再是周期性变化，显得杂乱无章，图4 混沌态下变换器的相轨迹线由无穷的且不闭合的轨线组成，具有无限嵌套的重叠结构。当以参考电流Iref作为变量参数进行仿真分析时，变化范围为0.5～4.2 A，其仿真结果与上文类似，此处不再赘述。

当变换器进入不稳定的混沌态时，非周期性变化的输出电压和电感电流产生振荡，峰值会使开关元件承受较大的应力从而导致开关损耗上升，此时器件的工作效率及可靠性都会下降，对于整个电路的稳定运行带来不利影响，需采取有效的混沌控制策略。

3 混沌控制策略应用

对延迟微分反馈控制应用于混沌状态下的Buck-Boost 变换器分析如下：将其固定于稳定状态的周期轨道上，设u(t)=为延迟微分反馈控制器，其是一种非线性控制器，控制效果仅取决于反馈系数k的大小；该控制结构相当于一个阻尼器，当时间变量微分减小为正阻尼，反之则为负阻尼。选择电感电流iL为控制对象作为反馈控制器，则加入延迟微分反馈控制后的Buck-Boost 变换器的状态方程模型如式（3）所示。

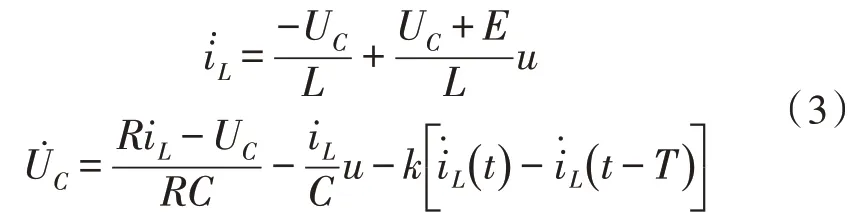
根据式（4）搭建加入延迟微分反馈控制后的Buck-Boost 变换器仿真模型，模型结构总体与图2 基本一致，不再敷述，执行仿真后的运行结果如图5～6所示，图5 为控制后电感电流iL的时域波形，图6 为控制后输出电压UC的时域波形。当反馈系数k=-60时，混沌状态下的Buck-Boost 变换器被控制在周期1轨道，如图5(a)、图6(a)所示；当k=-25 时，控制在周期2 轨道，如图5(b)、图6(b)所示；当k=-18 时，控制在周期4 轨道，如图5(c)、图6(c)所示；当反馈系数k=-15时被控制在周期8 轨道，如图5(d)、图6(d)所示。

由图5、6 的电感电流以及输出电压的仿真波形可见变化周期分别为0.05 ms、0.1 ms、0.2 ms、0.4 ms，对应时钟周期T=50 μs 的1、2、4、8 倍，Buck-Boost 变换器被控制到不同周期轨道上，混沌态得以消除，延迟微分反馈控制策略有效。

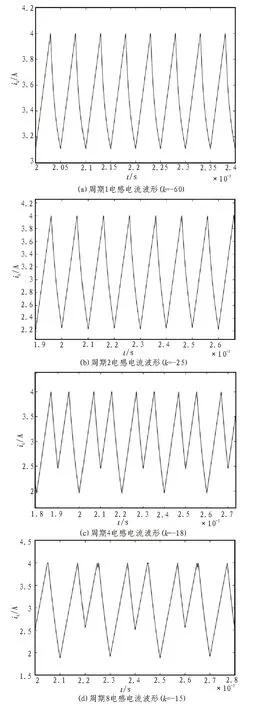
图5 不同反馈系数下电感电流时域波形

根据第1 节中的降升压变换器建模过程可知，输出电压UC是微分方程的另一状态变量，其仿真结果波形如图6 所示，将其与电感电流iL的结果对应观察可见变换器的混沌波形得到明显改善。

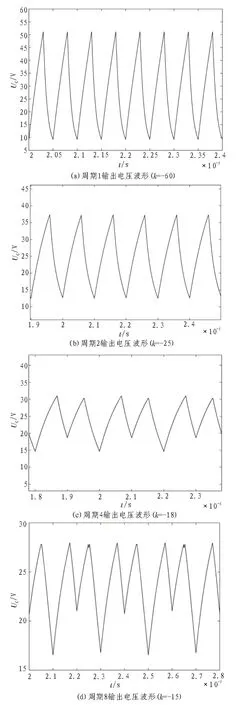
图6 不同反馈系数下输出电压时域波形

4 结论

文中通过MATLAB/Simulink 仿真软件搭建了电流模式控制的Buck-Boost 变换器的数学模型，选取恰当的电路参数使其运行于CCM 模式下，仿真分析得到变换器进入混沌态的现象，提出以延迟微分反馈控制作为混沌控制策略，仿真结果表明该策略能够将混沌态下的Buck-Boost 变换器重新控制在稳定的周期轨道上，仅需调节外部反馈系数k的大小即可实现控制在不同周期轨道上的效果，随着反馈系数的增大，控制周期也逐步提高；该控制结构较为简单，在电力领域中有较好的可实现性，同时也可将其推广应用于其他的直流变换器结构，对未来直流开关变换器实际应用场景下的混沌控制具有指导意义。