水平定向钻管道回拖影响因素的显著性分析

石贤增，李子涵，康小方

(安徽建筑大学 土木工程学院，安徽 合肥 230601)

非开挖技术在施工时不需要进行大规模的挖掘，可以在海洋、湖泊、高山等不同地质条件下使用，有较强的适应能力。同时非开挖技术降低了工程造价，对环境的扰动性小。1971年美国人Martin首次采用水平定向钻技术穿越哈罗河敷设管道获得成功[1-2]，目前该技术在国内外得到了广泛的研究与发展。Polak等[3]提出了聚乙烯管道在HDD施工过程中的回拖力计算公式；Cheng等[4]建立了水平定向钻施工中不同几何形状管道的回拖力计算公式；蔡亮学等[5-6]研究了木屑效应在水平定向钻回拖力预测中的分析与应用；汪爽[7]研究了不同管道吊装高度管道入土时夹角与管道回拖力之间的关系；常琼[8]通过有限元模拟了管道回拖台阶曲率、高度等因素对管道回拖力的影响；Dong等[9-12]对钻进泥浆及钻杆性能进行了模拟研究。

管道回拖力常受到曲率半径、孔管比、管道半径等多种因素的综合影响，且各因素对管道回拖力的影响程度存在较大差异。目前有关管道回拖影响因素差异性分析方面的研究较少。因此，为研究不同因素对所需最大回拖力的影响程度，本文选取影响直线段回拖力的4种因素，采用有限元模拟和理论分析相结合的方法，研究管道穿越时所需最大回拖力与其影响因素之间的关联度，旨在为工程中消除回拖力影响因素的方案设计提供参考。

1 管道回拖理论分析

1.1 管道台阶阻力模型建立

由于水平定向钻在施工时的实际受力情况与理论分析存在差别，且实际管道穿越轨迹与理论设计轨迹也存在差别，因此在进行理论计算时作出以下假设：①土体为刚性结构，受力不会产生位移与变形；②回拖管道均匀；③管道回拖轨迹与设计轨迹一致。管道穿越轨迹示意图如图1所示。

图1 管道穿越轨迹示意图

对管道直线段回拖时的受力情况进行分析，管道穿越台阶时的受力示意图如图2所示。管道回拖主要受到重力G、泥浆提供的浮力F浮、台阶产生的阻力ft、钻机提供的回拖力T以及管道外表面与孔道岩石表面之间的摩擦力f，故回拖力和浮力分别为：

图2 管道穿越台阶时的受力示意图

T=f+ft

(1)

(2)

式(2)中，D，d为管道内外径(m)；ρ1，ρ2为管道密度与泥浆密度(kg/m3)；L为管道长度(m)。

对竖直方向进行受力分析，可得：

F+Ncosα=G+μNcosβ

(3)

对水平方向进行受力分析，可得：

T=Ncosβ+μNcosβ

(4)

联合式(1)～(4)可得：

(5)

又由于α与曲率半径r、台阶高度h相关，故台阶阻力可表示为：

(6)

1.2 相关案例分析与计算

选取北京西六环路以东管道回拖工程的部分直线段(军庄镇西山林场范围)为例，工程高程为140～370 m，相对高程为15～250 m，山坡坡脚20～45°，山坡处多基岩裸露，山间谷地内覆盖碎石土，植被茂盛。穿越出、入土点的高差为13 m，角度为5～9°，穿越深度为18 m，穿越水平直线段为1 911.2 m，穿越平面曲线的起偏角为15°，回收角为7°，最大偏距为56 m，穿越工程总曲线长度为1 920.47 m，平直段长度为1 500.47 m。管道外径D=1.016 m，内径d=0.981 m，管道密度ρ1=7 850 kg/m3，泥浆密度ρ2=1 204 kg/m3，重力加速度g=9.8 kg/s2，回拖管道和岩土孔道之间的摩擦系数μ=0.3。

台阶阻力、台阶曲率与台阶高度的关系曲线如图3所示。从图3可以看出，当台阶高度一定时，随着台阶曲率增加，管道穿过台阶时所受到的阻力不断降低；横向比较发现，台阶曲率不变时，随着台阶高度的增加，管道穿过台阶时所受到的阻力也随之增大。

图3 台阶阻力、台阶曲率与台阶高度的关系曲线

2 管道回拖数值仿真分析

2.1 建立计算模型

为了具体分析各影响因素对管道回拖过台阶处回拖力的影响，运用有限元软件abaqus将现场工程回拖实际状况进行简化与模拟。建立模型时忽略管道回拖过程中的管道旋转，为提高计算效率，采用对称形式建立模型。所建模型包括土体、台阶和管道。建模型时，岩石高度为2 m，长度为20 m，宽度取1 m，管道半径R=0.4,0.5,0.6 m，孔管比为1.2,1.3,1.4,1.5,1.6，钻孔半径根据孔管比进行取值，台阶高度h=0.1,0.2,0.3,0.4 m,台阶曲率半径r=0.3,0.4,0.5,0.6 m,管道壁厚δ=0.02 m。

2.2 设置材料参数

管道弹性阶段材料密度为7 800 kg/m3，弹性模量为2.1×1011，泊松比为0.3。管道塑性阶段的应力-应变见表1。岩土塑性模型采用 Drucker-Prager 模型。该模型对于岩土等摩擦类材料的适用性强。岩土弹性阶段的密度为2 700 kg/m3，杨氏模量为4.13×1011Pa，泊松比为0.22。在D-P本构模型中，摩擦角β=44°，应变率为0.8，膨胀角φ=38°。岩石的硬化参数见表2。

表1 管道塑性阶段的应力-应变

表2 岩石的硬化参数

2.3 模拟施工阶段

回拖过程中管道与孔壁间的接触属性设置见表3。

表3 接触属性设置

2.4 设置边界条件与约束

采用对称建模，在管道与孔壁上设置对称约束。土体采用固定约束，在管道前端施加位移约束。对模型进行合理的网格划分，岩土模型采用四面体网格C3D10划分，管道采用四面体网格S4R划分，共划分36 168个网格。

3 仿真结果分析

3.1 台阶高度对管道回拖力的影响

当台阶曲率为0.5 m，管道半径为0.4 m，孔管比为1.5 m时，运用有限元软件模拟管道在不同台阶高度下管道回拖力的变化情况。不同台阶高度下管道回拖应力云图如图4所示。

(a) h=0.1 m

(b) h=0.2 m

(c) h=0.3 m

(d) h=0.4 m

从图4可以看出，管道最大应力应变出现在管道与台阶的接触面上，并随着台阶高度增加而增大。当h=0.1 m时，管道在经过台阶时所受到的应力为3.06×108Pa；当h=0.2 m时，管道与台阶接触面处受到的应力为3.06×108Pa。此时，管道受到的应力超过自身的屈服应力4.2×108Pa，开始产生变形；当h=0.3 m和0.4 m时，管道与台阶挤压面处受到的应力分别为7.9×108Pa和8.9×108Pa。此时，管道所受应力接近极限值，产生较大变形，在经过台阶时可能会产生破坏。

台阶高度对回拖力和应力的影响关系曲线如图5所示。从图5可以看出，随着台阶高度增加，管道经过台阶时受到的应力增加；当台阶高度由0.2 m增加到0.3 m时，管道所受应力出现明显的增长，接近管道受力极限。此时，管道可能在穿越台阶时产生了破坏，模拟研究意义不大，于是在后续模拟中台阶高度均取h=0.2 m；另一方面，随着台阶管道增加，管道回拖力增加。

图5 台阶高度对回拖力和应力的影响关系曲线

3.2 台阶曲率对管道回拖力的影响

当管道半径为0.4 m，孔管比为1.5，台阶高度为0.2 m时，台阶曲率对应力和回拖力的影响关系曲线如图6所示。

从图6可以看出，当台阶高度不变时，随着台阶曲率增大，管道经过台阶时所受应力逐渐降低，且回拖荷载也随之减小。这是因为当台阶高度不变时，随着管道曲率增加，台阶越平缓，管道经过台阶时与台阶接触相对平滑，接触面与之增大。故随着台阶曲率增大，管道所受应力逐渐降低，所需回拖荷载也逐渐减小。当r=0.3 m时，管道与台阶接触面所受应力为8.1×108Pa，此时管道在经过台阶时产生的变形较大，管道经过台阶处时可能会产生破坏；当r=0.5 m时，管道经过台阶时所受应力为5.0×108Pa；当r=0.6 m时，管道与台阶接触面的最大应力为4.2×108Pa，刚达到管道塑性应力极限。

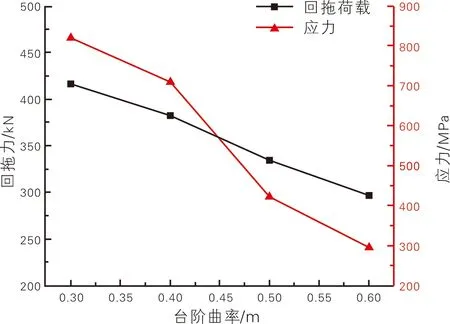
图6 台阶曲率对应力和回拖力的影响关系曲线

3.3 管道半径与孔管比对管道回拖力的影响

管道半径与孔管比对回拖力的影响关系曲线如图7所示。

图7 管道半径与孔管比对回拖力的影响关系曲线

从图7可以看出，当管道半径不变时，随着孔管比增加，管道回拖力减小。这是因为孔管比越大，孔道半径越大，管道在回拖时与孔壁接触产生的摩擦阻力越小，所以回拖力越小。当孔管比≤1.4时，随着孔管比增加，回拖力的降低相对明显；当孔管比>1.4时，随着孔管比增加，回拖力的降低相对平缓；当孔管比从1.5增长到1.6时，回拖力降低不明显。这可能是因为孔管比达到某一数值后，随着孔管比增加，回拖力不再降低。当孔管比不变时，随着管道半径增大，管道回拖力增大。这是因为孔管比不变时，管道半径增大，管道回拖时与孔壁产生的摩擦阻力越大，故所需要的回拖力越大。

4 关联度分析

管道回拖力受到台阶高度、台阶曲率、管道半径等多种因素的共同影响。为研究各因素对管道回拖的影响程度，采用灰色理论，计算分析各种因素与管道回拖力之间的关联度。灰色关联度分析主要是通过比较数列和参考数列的曲线形状相似度来判断各个比较序列间与参考数列的密切程度，二者曲线形状越靠近，所对应的序列之间关联就越密切，反之就说明二者对应的序列关联度越小。灰色理论分析的衡量工具就是关联度系数，用于衡量二者序列之间的密切程度[13-18]。

灰色关联度分析数列行为序列公式为：

Xi(K)=(x1(1),x2(2),…,xi(n))

(7)

对行为序列进行初值项计算，公式为：

Xid1=(x1(1)d1,x2(2)d1,…,x1(n)d1)

(8)

行为数列的均值项公式为：

Xid2=(xi(1)d2,xi(2)d2，…，xi(n)d2)

(9)

对最大差值与最小差值求解，公式为：

(10)

式(10)中，Δi(k)=|x0(k)-xi(k)|；i=1,2，…，n；k=1,2，…，n。

关联度系数计算，公式为：

(11)

式(11)中，ζ=0.5；k=1,2，…，n；i=1,2，…，m。

通过有限元软件分别模拟不同影响因素下管道回拖力的变化情况。不同影响因素下模拟实验结果见表4。

表4 不同影响因素下模拟实验结果

选取20组不同回拖力数据对其各因素进行关联度分析，步骤如下。

1)各数列初值化处理。对比数列是事件系统的影响因素，参考数列反应系统行为特征。将表4中的最大回拖力作为参考数列，4个影响因素作为对比数列，初值化数列可以表示为：

ωi=(ω1(1),ω2(2)，…，ω1(k))

(12)

2)变量均值化处理。为了消除各比较数列量纲对分析结果的影响，需要对各数列进行均值化处理，公式为：

(13)

3)计算各对比数列与参考数列差值。分别求出对比数列与参考数列的绝对差，并求得绝对差的最大值和最小值，公式为：

Δ0i=|x0(k)-xi(k)|

(14)

(15)

(16)

4)计算关联度系数。根据上述计算所得数据求得关联度系数，计算公式为：

ε(x0(k),xi(k))=minminΔ0i(k)[Δ0i(k)+ξmaxmaxΔ0i(k)]-1

(17)

式(17)中，ξ=0.5。

5)关联度计算。将计算得到的关联度系数平均值作为对比数列与参考数列之间的关联度。计算公式为：

(18)

式(12)～(18)中，k=1,2,…，20；i=0,1,2,3,4。

根据式(18)计算出各对比数列关联度并进行排序。各影响因素与回拖力的关联度及排序见表5。

表5 各影响因素与回拖力的关联度及排序

从表5可以看出，引起管道回拖力变化的关联度排序为：台阶曲率>台阶高度>管道半径>孔管比。

5 结论

1)随着台阶高度增加，管道回拖所受应力与所需回拖力增加；当台阶高度一定时，随着台阶曲率增加，管道穿越台阶时与台阶接触越平缓，所需回拖力越小。

2)在不同的孔管比下，管道回拖所需要的回拖力随着孔管比增大而减小，但是当孔管比>1.4时，回拖力随着孔管比增加降低趋于平缓，故孔管比达到某一具体数值时，将对管道回拖力不再产生影响。

3)利用灰色理论对影响管道回拖力的因素进行了关联度排序，得出影响回拖力因素顺序依次为：台阶曲率>台阶高度>管道半径>孔管比。