永磁同步直驱式带式输送机多电动机功率平衡控制策略

黄海飞

(中国煤炭科工集团 太原研究院有限公司， 太原 030006)

0 引言

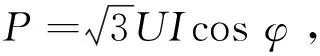
1 永磁同步直驱带式输送机

1.1 基本结构介绍

永磁同步直驱带式输送机滚筒布置结构以图1为例，驱动电动机与滚筒直接互联并通过摩擦力直接驱动带式输送机运行。

图1 永磁直驱式带式输送机结构

图1所示为3台永磁同步电动机(Permanent magnet Synchronous motor，PMSM)直接驱动负载的带式输送机结构，PMSM1与PMSM2为刚性连接，直接驱动滚筒A；PMSM3直接驱动滚筒B；滚筒A与滚筒B之间为柔性连接，由输送带互联。PMSM1、PMSM2以及PMSM3的额定功率、基本参数相等，共同驱动带式输送机实现物料、煤料的运输。

1.2 基本原理分析

对带式输送机多电动机功率平衡控制时采用自抗扰控制技术(Auto-disturbance Rejection Controller，ADRC)，将带式输送机前后滚筒的PMSM1、PMSM3、PMSM3的不确定因素视为未知扰动，对输入、输出参数进行相应的控制后便可对未知扰动进行精确估算和实时补偿，消除控制误差。ADRC由跟踪微分器TD、扩张状态观测器ESO、非线性状态误差反馈控制规律NLSEF三部分组成，TD可有效改善传统控制系统存在的初始误差较高、超调严重的问题，如假设系统误差为e=v-y，其中v为设定值，y为输出值。采用TD后，可对设定值v合理过度至v1(t)，由TD对微分信号进行提取，系统误差可调节为e=v1(t)-y，达到减小误差、降低超调的目的[6-7]。ESO可解决传统PID控制器无法对控制系统进行实时估计的问题，将控制系统的所有扰动视为控制系统的一种状态，无需进行扰动类别的识别和测量。ESO只根据控制系统的输入、输出信号就可构建控制系统原态和扩张态，完成对控制系统的补偿。ELSEF即利用非线性函数fal、fhan解决传统PID控制器控制量误差非最优的问题，如fal函数可表示为式(1)：

(1)

由式(1)可知，α越小，控制系统的跟踪速度越快，但滤波效果越差；δ越大，滤波效果越好，但跟踪速度较差；且α<1时，fal函数具有小误差、大增益或者大误差、小增益的特性，有效抑制控制系统的稳态误差。

自抗扰控制器中的NLSEF误差增益系数β在外部干扰较大时智能依靠控制经验进行手动调节，因此引入模糊控制理论对NLSEF参数进行模糊整定，达到ADRC参数实时修正的目的。模糊自抗扰控制器原理如图2所示，电动机的误差e以及误差变化率ec作为模糊控制器的输出为NLSEF的整定参数Δβ。

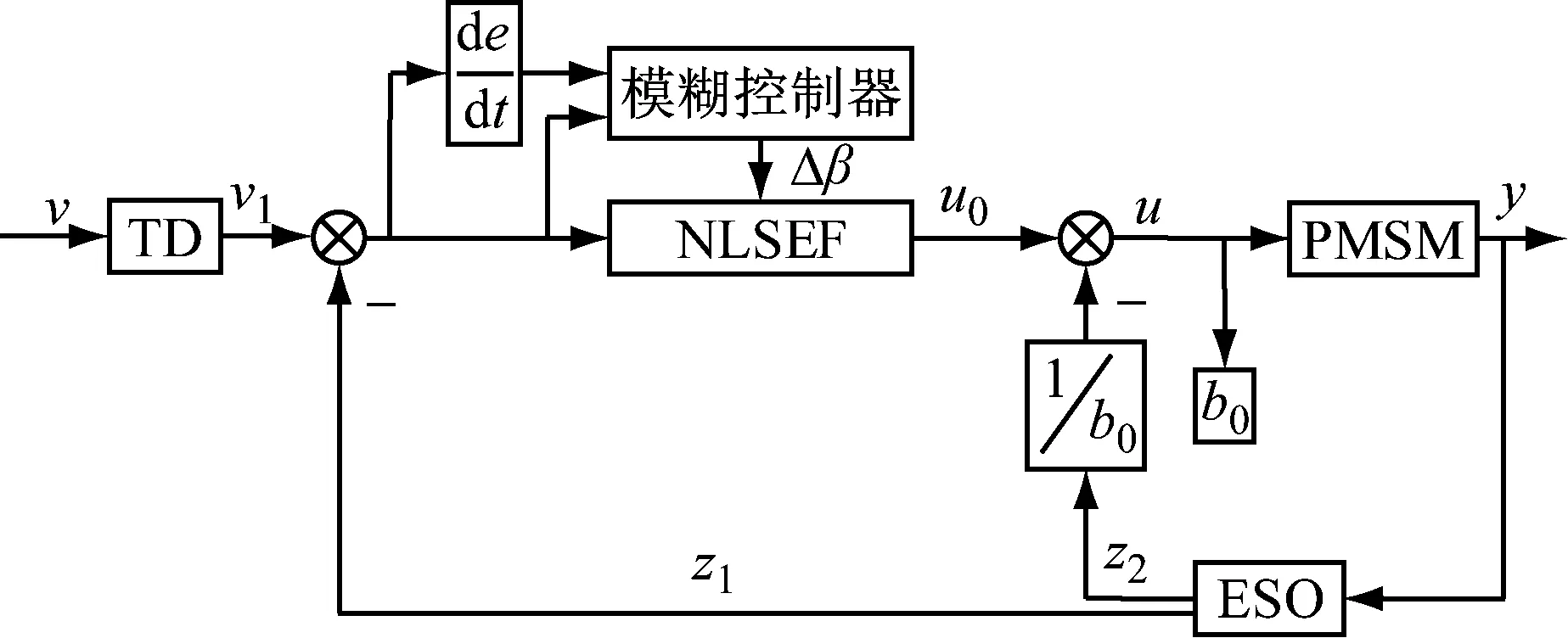
图2 模糊自抗扰控制器原理

2 功率不平衡问题分析

定义带式输送机负载率为电动机实际输出功率与额定功率之比，则只要确保各电动机的负载率相等即可达到多电动机功率平衡的目的。定义PMSM1、PMSM2以及PMSM3的实际输出功率、额定功率分别为P1、P2、P3、PN1、PN2以及PN3，理想负载率为ξN，实际负载率为ξi，则得式(2)、式(3)：

(2)

(3)

当多电动机功率平衡时，满足式(4)：

ξN=ξii=1,2,3

(4)

定义带式输送机电动机的功率不平衡度为Ωi，可表示为式(5)：

(5)

由电动机运动方程可知，影响带式输送机电机功率不平衡的因素主要有输送带宽度、输送带弹性模量、输送带阻力、输送带与滚筒的应变差、滚筒半径以及电动机定子电流频率[8]。

3 多机功率平衡控制策略研究

3.1 转矩分配

3台永磁同步电动机驱动的带式输送机驱动电动机功率分配按照式(6)进行：

(6)

式中:Pi为永磁电动机1/2/3分配的给定功率；Pei为永磁电动机额定功率；P为负载功率，且满足P=P1+P2+P3；n为永磁同步电动机数量，数值为3，且满足永磁同步电动机1/2/3的型号、参数完全相同。

3台永磁同步电动机带式输送机系统运行时满足式(7)：

(7)

式中:P1、P2以及P3为3台永磁同步电动机各自的输出功率，单位为kW；T1、T2以及T3为各永磁电动机的电磁转矩，单位为N·m；ω1、ω2以及ω3为各永磁电动机的角速度，单位为rad/s。带式输送机运行时，在保证3台永磁同步电动机转速相等时，对电动机电磁转矩T进行控制即可完成负载功率均衡分配，可表示为式(8)：

(8)

式中:T为带式输送机负载转矩，Tei为各永磁同步电动机的额定电磁转矩，单位为N·m。根据图1，设定PMSM1为主运动电动机，PMSM2以及PMSM3为从运动电动机，则3台永磁同步电动机转矩分配可表示为式(9)：

开展此项工作前要让人们深入了解此类疾病的传播途径，最大限度地提升人们的思想意识，进而提升预防的力度。结合牲畜饲养状况对完善的消毒工作制度进行构建，牛场的设计要将国家动物卫生防疫方面的要求作为根本依据，将消毒池和消毒间设置在门口；推行封闭式的饲养管理模式，确保饲养人员工作服的清洁，车辆以及行人等不可随意进出饲养场内部；牲畜饲养间保证每周最少彻底消毒1次，可采用2%福尔马林溶液、20%的石灰乳、1%或3%的石炭酸溶液、3%的漂白粉溶液或苛性钠溶液进行消毒，消毒效果比较理想。

(9)

当带式输送机的PMSM1、PMSM2以及PMSM3的型号、参数一致且滚筒A、滚筒B负载分配比例为2∶1时，K=1。

3.2 功率平衡控制

以双滚筒三电动机煤矿井下带式输送机为例，基于偏差耦合结构对3台永磁同步电动机的转速、电流进行采集、控制并经Clark、Park坐标变换后得到三电动机的转矩电流值iq，通过iq标识三电动机输出功率，达到带式输送机三电动机功率均衡分配的目的。永磁同步直驱式带式输送机偏差耦合控制系统如图3所示[9-10]，实时采集、检测3台电动机的转速、电流，同时利用补偿器将非本台电动机的转矩电流偏差值补偿至本电动机并对电动机转速进行调节，使得3台电动机的运行工况一致、同步并达到功率平衡控制。

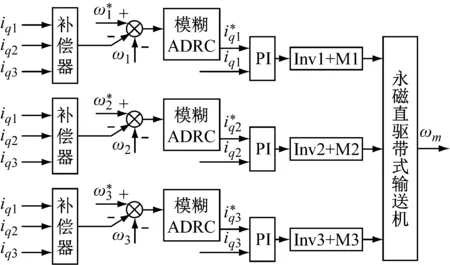
图3 3台永磁同步电动机直驱的带式输送机偏差耦合控制系统

基于偏差耦合结构的带式输送机多电动机功率平衡过程为：当任意一台永磁同步电动机的负载发生变化时，PMSM1、PMSM2以及PMSM3的转矩电流会存在偏差，3台电动机输出功率出现不平衡；对其余2台PMSM的转矩电流与本台PMSM转矩电流进行比较并利用补偿器对电流偏差值进行补偿；基于电流偏差值实现对PMSM转矩电流的动态调节。PMSM1、PMSM2以及PMSM3转矩电流可形成耦合环，转矩电流偏差与转速偏差补偿可互为补充，从而使得转矩电流实现动态平衡，最终实现PMSM1、PMSM2以及PMSM3功率负载均衡分配。

图4所示为PMSM1的偏差耦合补偿器结构，即PMSM1的负载变化或者扰动较大时，转矩电流值与PMSM2、PMSM3的转矩电流值会存在较大偏差，基于图4偏差耦合补偿器结构，将转矩电流偏差值补偿至其他2台电动机，并在3台电动机之间形成耦合环，实现三电动机负载均衡分配，提升系统抗干扰能力，即将PMSM1的转矩电流偏差分散至PMSM2以及PMSM3中，使得三电动机驱动系统运行状态保持一致，输出为Δω。

图4 偏差耦合补偿器结构

4 多机功率平衡控制系统仿真

为验证3台永磁同步电动机直驱的带式输送机偏差耦合控制系统，根据图3控制系统原理搭建仿真模型，并对设计的多电动机功率平衡控制系统的正确性、有效性进行验证。PMSM1、PMSM2以及PMSM3的额定功率相等，定子电阻分别为0.05 Ω、0.054 Ω、0.058 Ω，采用模糊ADRC控制算法完成带式输送机三电动机功率平衡方案仿真对比以及空载启动、带载启动仿真试验。

4.1 功率平衡方案仿真对比

带式输送机空载启动后，给2台电动机添加初始负载80 N·m，0.4 s时将电动机2的负载增加至120 N·m，电动机1的负载保持不变，分别采用无模糊ADRC控制功率平衡方案和有模糊ADRC控制功率平衡方案完成仿真，转矩波形曲线如图5、图6所示。由图5和图6仿真结果可知，无功率平衡控制方案时，系统不会进行负载分配，电动机输出转矩不均衡；采用功率平衡控制方案后，2台电动机负载变化且不一致时，输出转矩能够保持一致，首先负载均衡分配。

图5 无功率平衡方案电动机转矩波形

图6 有功率平衡方案电动机转矩波形

4.2 空载启动仿真

图7 空载启动转矩波形

图8 空载启动电流波形

4.3 带载启动仿真

带式输送机带载启动，初始负载为85 N·m，运行至0.3 s时增加负载180 N·m，PMSM1、PMSM2以及PMSM3的转矩曲线、电流曲线见图9、图10。在0.3 s时，带式输送机负载突然增加时，3台电动机的转矩、电流能够在短时间内快速响应并达到稳态，且始终保持Te1=Te2=Te3、i1=i2=i3，保证3台电动机处于平衡状态，实现3台电动机负载均衡分配。

图9 带载启动转矩波形

图10 带载启动电流波形

由带式输送机空载启动、带载启动仿真试验表明，基于偏差耦合结构的三电动机功率平衡控制策略能够实现带式输送机前后电动机的负载均衡分配，按照控制系统分配比例均衡驱动，防止单电动机出现过载、过流现象，实现多机功率平衡控制。

5 结论

1) 对矿用永磁同步直驱式带式输送机结构进行分析，由刚性+柔性连接的PMSM1、PMSM2以及PMSM3组成。

2) 对模糊自抗扰控制技术基本原理进行分析，能较好地解决带式输送机多电动机控制系统存在外部干扰大、无法建立精确模型的问题。

3) 在分析带式输送机多电动机控制系统功率不平衡因素的基础上，以偏差耦合结构为基础，基于模糊自抗扰控制技术设计多电动机功率平衡控制策略。

4) 基于设计的多电动机功率平衡控制策略，完成空载、带载仿真，试验结果验证了所设计控制策略的正确性和可用性。