基于特征点的SAR影像配准方法

刘智勇 来立永 张耿斌 祁宏昌潘屹峰 彭林才 吴希文

1)广东电网有限责任公司， 广州供电局， 广州 510620 2)中科云图科技有限公司， 郑州 450003 3)广东工业大学， 土木与交通工程学院， 广州 510006 4)广东工业大学， 大湾区城市环境安全与绿色发展教育部重点实验室， 广州 510006

0 引言

合成孔径雷达干涉测量技术(Interferometric Synthetic Aperture Radar， InSAR)已被广泛应用于自然灾害的监测工作中， 如地震(Wangetal.， 2007， 2009， 2019)、 地表沉降(王华等， 2014a； Ngetal.， 2018)、 滑坡(Tarchietal.， 2003； Sunetal.， 2015)等。通常， 在形成干涉图之前需对SAR影像进行配准并重新采样到与参考影像(主影像)统一的网格上。配准作为InSAR数据处理的关键步骤， 其精度直接影响InSAR生成干涉图的质量。为了不影响生成干涉条纹的质量， 对于Stripmap/ScanSAR成像模式的影像配准误差必须要控制在0.125个像素以下(王超等， 2002)， 对于方位向渐进式扫描的地形观测(Terrain Observation with Progressive Scans in azimuth， TOPS)成像模式， 其配准精度需要达到千分之一个像素才不至于影响干涉处理(吴文豪等， 2017)。

SAR影像配准主要用于匹配多时相、 多传感器或从不同视点拍摄的2个或多个影像(Brown， 1992)。常规的配准方法是在主强度图上按照一定的间距规则选取控制点， 即规则点(Regular Points， RP)。由于规则点的选取不考虑地面的散射特性， 在具有较高相干性的区域效果较好， 但在实际应用中， 规则点经常位于低相干、 失相干区域(例如大面积的水域、 植被茂密的森林或季节变化的农业区域等)， 导致配准存在计算量大、 误匹配率高以及可靠性低等缺陷。

为了改善常规配准方法所存在的缺陷， 一些研究人员利用永久散射体(Permanent Scatterer， PS)、 孤立点(Isolated Points， IPs)等特殊点目标替代规则点进行配准。虽然PS点具有很好的稳定性， 但PS点的可靠识别需要大量SAR影像， 而研究中通常只有很少的数据可用， 致使此方法受到较大的限制。此外， IPs通常是孤立的比较明亮的点(Serafino， 2006)， IPs能有效避开失相干的区域(例如水体)， 但由于SAR影像的成像特性， 这些亮点可能会聚集在一定的空间中， 因此可能会导致类似斑状的偏移估计。此外， SAR影像中存在大量的斑点噪声， 呈现出高亮度值， 同样会导致孤立点定位错误。

配准的主要目的是获取主、 辅影像之间的坐标转换参数， 除了PS点和IPs点之外， 可利用具有明显特征的点进行配准， 因此， 特征提取是SAR影像配准技术中的关键， 准确的特征提取为配准的成功进行提供了保障。Bay等(2006)提出的加速鲁棒特征算子(Speeded Up Robust Feature， SURF)算法是用于遥感影像特征检测与描述的流行方法之一， 其可利用SURF算子对SAR影像进行配准(熊智等， 2011； Durgametal.， 2016)。但由于SAR影像在成像时存在大量噪声点， 仅通过使用SURF算法进行配准的精度低且误匹配率高， 难以满足InSAR的精度要求。

针对上述配准问题， 本文提出了一种结合SURF、 土地覆盖数据和互相关算法等的配准方法。首先， 对主强度图进行分块处理， 并将每个子块数据的灰度值线性拉伸到0～255； 然后， 通过SURF对每个子块进行特征点探测， 接着利用土地覆盖数据剔除不当的特征点， 对保留的特征点进行互相关； 最后， 通过多项式拟合获取主、 辅影像之间的仿射变换参数。本文通过珠三角地区的SAR影像数据的配准实验评估该方法的性能。

1 Sentinel-1A雷达数据及配准方法

1.1 数据

本文所用的研究数据覆盖了广州、 佛山、 东莞等珠三角地区， 采用2015年12月12日以及2015年12月24日的一对C波段Sentinel-1A雷达影像数据， 其成像模式为TOPS模式， 影像大小为20278像素×68514像素， 在距离向和方位向上的像素大小为2.3m×14.1m， 空间分辨率为5m×23m。

1.2 基于特征点的SAR影像配准

标准的配准方法首先在主强度图上按照等间距选取控制点， 然后采用相关系数法进行像素级配准， 接着进行过采样处理， 并再进行一次互相关以实现亚像素级配准， 最终进行多项式拟合计算主、 辅影像之间的转换参数(靳国旺， 2007)。本文提出的SAR影像配准方法首先利用SURF算子探测主影像的特征点(Feature Points， FP)， 然后进行水体掩膜， 剔除无效特征点， 并对保留的特征点进行互相关， 最后进行多项式拟合获取主、 辅影像之间的转换参数。

1.2.1 利用SURF提取特征点

SURF算法是由Bay等(2006)提出的尺度与旋转不变的兴趣点检测和描述符， 是改进尺度不变特征变换算子(Scaleinvariant feature transform， SIFT)(Low， 2004)的一种特征检测算法， 在独特性和鲁棒性方面均近似甚至优于SIFT， 且计算速度快于SIFT。其特征点提取主要流程是：

(1)构造Hessian矩阵， 并通过Hessian矩阵的行列式初步判定特征点位置

当行列式值为0时， 可判定该点比邻域内的其他点更加明亮或者暗淡。为提高计算性能， SURF使用盒式滤波器模板代替高斯二阶微分模板。图 1 为9×9的盒式滤波器， 左侧2张图分别是y方向和xy的二阶高斯微分模板， 右侧2张图是采用盒子滤波器对其近似的结果， 模板中的数字(-1、 1、 -2)表示对应颜色区域的权值， 灰色区域权值为0。因为盒式滤波器在积分影像上的计算速度非常快， 故SURF与SIFT相比在性能上有了很大的提升。

图 1 盒式滤波器模板示意图Fig. 1 Schematic diagram of box filter template.

(2)建立影像金字塔

SIFT通过保持滤波器模板不变， 对原始影像进行降采样获得影像金字塔(图 2a)。SURF通过改变滤波器的尺寸而影像不变来保持尺度不变性(图 2b)。与SIFT相比， SURF具有更快的速度和更高的精度。

图 2 影像的金字塔Fig. 2 The image pyramid.

(3)定位特征点

经Hessian矩阵处理后的像素点须与相同或相邻尺度空间中的26个像素进行比较(图 3)， 滤除响应值较弱及错误定位的像素点， 并选定稳定像素点作为特征点。

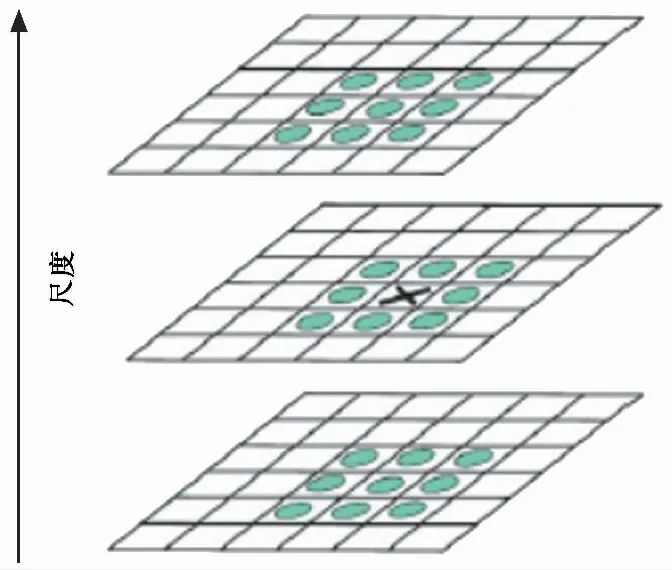
图 3 特征点定位Fig. 3 Location of feature points.

SAR影像的成像过程是由不同散射体的回波路径相干叠加而成， 导致SAR影像中存在大量或明或暗的斑点， 即相干斑(Eom， 2011)， 这降低了SAR影像的目标识别能力。为了抑制SAR影像的相干斑， 可进行多视处理， 但该处理同时会降低SAR影像的分辨率。本文中， 为在确保不牺牲SAR影像分辨率的前提下提高特征点识别的速度并抑制噪声， 首先对每个子块的灰度值进行初步处理， 以保证整体影像不会太明亮或太过暗淡。在0.5%≤灰度值 ≤99.5% 的范围内将其进行线性拉伸到0～255， 对于灰度值 >99.5% 或 <0.5% 的像素则分别设置其值为255和0。对主强度图进行初步处理后， 使用SURF算子探测特征点。SURF可处理大块数据， 具体窗口大小可根据计算机的物理内存进行配置。本文为加快计算速度并防止整个检测窗口位于水体中， 统一将特征点的探测窗口大小设置为5000像素×5000像素。

从图 4 中可以比较明显地看出水体与陆地之间的灰度值差异， 这对陆地特征点的准确定位有所帮助。设置Hessian的阈值为25000， Octaves为4， Octaves layers为3， 一共探测到了8693个特征点， 大部分都集中于陆地(图4a中的红色圆圈)， 但有一部分特征点仍落入水体中(图4a中的蓝色圆圈)， 其主要原因是在珠江流域及入海口停泊了大量船只。图4a黄色方框区域的放大图如图4b、 c所示， 从图4b中可以明显看出这些船只在雷达强度图中相对于周围水体具有非常明显的差异， 导致SURF将其识别为特征点(图4b右侧)。但经过一段时间后在相同区域再次进行检测， 探测到的特征点位置随船只的移动具有很大的差异(图4c右侧)， 而陆地上探测到的特征点仍然具有非常稳定的特性， 其相应的位置基本保持不变。因此， 在进行配准之前， 需利用外部土地覆盖数据剔除落入水中的特征点， 以剔除不稳定的特征点。

图 4 特征点分布图Fig. 4 Distribution map of feature points.a 主强度图的特征点； b 主影像局部特征点； c辅影像局部特征点

1.2.2 水体掩膜

在水域中， 干涉图的相干性均非常低(接近0)(王华等， 2014b)。同样， 在大面积水域中进行互相关， 相关度极低且偏移量极不稳定， 这不仅大大降低了配准的计算效率， 同时还导致错误的偏移量估计， 使得最终计算的主、 辅影像转换模型不可靠， 故必须对水体进行掩膜处理。尽管SURF可有效避开水体， 但当Hessian阈值太低、 探测窗口太小或整个探测窗口都在水中时， SURF探测到的特征点可能位于水中。因此， 针对在主强度图中探测到的特征点需要进行水体掩膜处理， 以剔除位于水体中的特征点。

本文利用SWBD(Shuttle Radar Topography Mission Water Body Dataset)数据滤除SAR强度图中不适当的特征点， SWBD数据可从相关网站(1)http: ∥geodata.policy support.org/swbd。下载。SWBD数据是仅有-1和0的二值二进制文件， -1为水体， 0为陆地。由于SWBD是地理坐标， 而强度图是雷达坐标， 故需要将SWBD数据转换到雷达坐标系下， 判断特征点所在位置的SWBD值是否为0， 否则舍弃。

1.2.3 互相关计算

经水体掩膜后， 进行互相关计算。互相关可衡量2幅影像的相关程度， 计算公式为

(1)

式中，M、S表示主、 辅影像的强度，E为求平均。当|ρ|=0时， 表示主、 辅影像完全不相关； 当|ρ|=1时， 表示主、 辅影像完全相关。

图 5 左侧是主强度图的参考窗口m，m的窗口大小一般取2的倍数， 如32×32、 64×64、 128×128等， 中间是辅强度图的搜索窗口s，s的窗口尺寸必须>m， 红框是与m窗口大小相等的辅匹配窗口s0， 右侧为相关系数ρ， 计算的过程为： 保持m不变，s0逐行逐列地在s内移动， 每移动1次， 就利用式(1)计算1次m与s0之间的相关系数ρ， 并记录此时计算得到的相关系数、 信噪比以及方位向和距离向的偏移量， 依次遍历整个搜索窗口。最终， 相关系数极值所在的位置对应的偏移量， 即为2幅影像的最佳偏移。

图 5 互相关计算示意图Fig. 5 Schematic diagram of cross-correlation calculation.

1.2.4 多项式拟合

通过互相关计算得到所有控制点的偏移量后， 再进行多项式拟合， 计算模型如式(2)所示， 可初步通过设置阈值剔除粗差， 如设置SNR>5或相关系数>0.45， 并对剩下的数据通过最小二乘反演主、 辅影像之间的几何转换参数， 删除超限值， 然后重新计算转换参数， 不断迭代计算， 直到剩下的所有数据满足条件为止。对于主、 辅影像而言， 只有1组转换参数， 即旋转参数(m1，m2，m3，m4)与平移参数(m5，m6)， 而(x1，y1)、 (x2，y2)分别为主、 辅影像的像素坐标。

(2)

2 标准配准方法与基于特征点的配准方法的比较

我们首先对特征点和规则点分别在距离向和方位向的偏移量进行了比较。图6a与6b是经过水体掩膜后整个SAR影像偏移量的统计直方图。规则点的取样间隔为256像素×512像素， 为了更加客观地比较， 设置Hessian阈值为25000， 获取的特征点数量与规则点的数量接近。由于本文所选的雷达数据不存在变形或偏移量小于配准所能识别精度的情况， 偏移量一般呈现为常数或按照一定规律变化， 本文通过偏移量与0之间的偏差评估算法的准确性。我们以十分之一个像素作为评估指标， 经过水体掩膜后， 在距离向上基于特征点的配准方法获取的偏移量约有80%介于-0.1～0.1像素之间， 而标准的配准方法仅有约54%； 在方位向上， 分别有82%、 62%的偏移量介于-0.1～0.1像素之间， 可见本文提出的方法所获得的偏移量更加稳定可靠。

图 6 特征点和规则点的偏移量及相关系数比较Fig. 6 Comparison of offset and cross correlation between feature points and regular points.a 距离向偏移量统计； b 方位向偏移量统计； c 相关系数统计

互相关系数是互相关质量的重要指标， 因此， 接下来将对规则点以及不同Hessian阈值的特征点所获取的相关系数进行对比。图6c为互相关系数的概率分布， 互相关系数越高表示互相关越稳健， 偏移量将更精确。标准配准方法的峰值约为0.4， 本文提出的配准方法的峰值约为0.9， 远远高于前者。通常认为相关系数>0.45的配准是相对可靠的， 我们统计了这2种方法相关系数>0.45的同名点数量， 其中标准方法仅有约43%， 而本文提出的方法 >94% ， 具有非常明显的优势。此外， 随着Hessian的阈值从25000增加到34000， 特征点的数量减少， 通常获取的相关系数整体将提高， 但Hessian增加到达一定的程度后， 相关系数的峰值就不再增大， 所求得的相关系数已无法进一步提高， 而是更多集中于高相关性区间， 这与获取的SAR影像数据的质量相关。

之后， 为了测试本文提出方法的性能， 我们分别评估了利用特征点与规则点进行多项式拟合的精度与效率。利用式(2)对偏移量数据进行最小二乘估计， 设置后验标准差为0.05， 如果计算的残差值超过了后验标准偏差的1.5倍则将其剔除， 接着利用余下的数据进行迭代计算， 直到所有数据的残差值符合条件为止。

首先对主强度图设置256像素×512像素的间隔， 获取了8821个规则点， 作为比较， 设置Hessian为25000， 获得8693个特征点。在迭代反演中， 规则点和特征点分别保留了为56%和18%。接下来， 进一步提高Hesssian阈值至34000， 获取了2164个特征点， 经计算其得到与8821个规则点的精度近似甚至更好， 对主、 辅影像的转换参数模型的约束同样好。这说明在配准的过程中， 利用规则点进行互相关计算浪费了大量时间， 且在相同的精度条件下， 特征点的数量和计算时间仅约为规则点的1/4， 可极大提高配准效率。

3 智利地震

3.1 数据

2015年9月16日， 智利Illapel的近海发生了8.3级强烈地震， 且引发了海啸(2)http://earthquake.usgs.gov/。， 其首都圣地亚哥震感强烈。本文使用的数据是2015年8月26日与2015年9月19日018轨道的Sentinel 1A的SAR影像数据， 通过偏移追踪研究2015年智利MW8.3地震产生的同震形变场， 并对本文提出的方法进行验证。

3.2 基于FP的偏移追踪

配准获得的偏移量可直接应用于地表形变研究， 即进行密集的配准， 称为偏移追踪。常规的偏移追踪(Regular Points Offset Tracking， RPOT)估计的是均匀分布于2个SAR影像上同名点之间的变形， 不考虑地面的散射特性， 从而导致配准或偏移追踪的效率低下且结果不可靠。下面对常规偏移追踪和特征点偏移追踪(FP Offset Tracking， FPOT)进行比较。RPOT设置规则点间距为32像素×32像素， 并进行偏移量计算， 结果如图7a、 b所示， FPOT设置Hessian阈值为6000以获取特征点， 然后进行偏移量计算， 结果如图7c、 d所示。FPOT和RPOT均屏蔽水体， 通过对比可以发现， RPOT的偏移量结果中含有大量噪点， 特别是图7a、 b的左下角与右上角， 其中左下角是海洋， 右上角是植被茂密的森林， 获取的偏移量极不可靠。由于在海洋或森林中极少存在特征点， 因此FPOT能很好地规避这些低相干区域， 可见本文提出的方法适用于植被茂密、 水体覆盖率大等复杂而又易失相干的区域， 极大提高了计算的效率和可靠性。

图 7 智利地震初始偏移量散点图Fig. 7 Scatter plot of initial offset of Chile earthquake.a RPOT距离向偏移量； b RPOT方位向偏移量； c FPOT距离向偏移量； d FPOT方位向偏移量

3.3 实验结果

为了移除噪点对多项式模型的影响， 将相关系数<0.45或者信噪比<5的同名点予以剔除， 并屏蔽形变近场进行多项式拟合， 获取偏移量残差， 最后进行滤波处理。为了能更有效地比较FPOT和RPOT的性能， 在进行水体掩膜后， 对偏移追踪数据设置相同的参数， 以获取最终的变形场， 如图 8 所示。最终， FPOT约保留了75%的数据， 而RPOT仅保留了约30%的数据， 可见前者极大提高了偏移追踪的计算效率。此外， 与GPS观测数据进行了对比， 在距离向、 方位向与GPS的均方根RMS分别约为15cm、 19cm， 精度约为 1/15 像素。

4 结论

精确配准是InSAR数据处理的关键。标准的配准方法存在冗余计算、 相关性低或可靠性差等缺陷。为了提高标准配准方法的可靠性和效率， 我们提出了一种利用特征点进行配准的方法， 该方法结合了特征点探测、 水体掩膜以及互相关等步骤。通常情况下， 如果地表类型差异大、 强度图区分明显， 常规配准算法也能获得较好的配准效果， 此时配准方法对结果影响较小。然而， 在地表植被茂密或者水体较多的情况下， 配准精度较难提高， 本文旨在解决这方面的问题。通过对珠三角地区的SAR影像数据的配准实验以及智利地震的偏移追踪的应用表明， 与标准的配准方法相比， 基于特征点的配准方法适用性广， 并能实现更高的互相关度， 从而获得更加可靠的偏移估计， 并能以更小的计算量达到与标准方法相同的精度， 进一步提高配准效率。