基于VMD的ZPW-2000A型轨道电路复杂故障特征提取方法研究
张帅,周游,赵少翔
ZPW-2000A型无绝缘轨道电路已被广泛应用于我国铁路列车运行控制系统中。由于其各部分组成较为复杂,在列车实际运行中,维护人员对一些设备组合故障的诊断经验不足,导致故障处理不及时,严重影响了铁路运输的安全和效率。根据现场统计发现,受列车运行产生的振动冲击、恶劣气候、牵引电流等因素导致的冲击电压影响,轨道电路设备发生故障的概率最大,其中补偿电容和调谐区内调谐单元BA1、BA2、空心线圈SVA的故障又占轨道电路总故障率的95%以上[1]。随着铁路运营里程的不断增加,研究ZPW-2000A型无绝缘轨道电路的故障特征,实现对轨道电路全面、准确的诊断,对提高铁路运营的安全性和可靠性都有着十分重要的意义。
为了改善铁路现场电务检测车对轨道电路故障巡查的传统方式,国内外学者采用不同的方法对轨道电路进行故障诊断。文献[2]采用时频分析的方法,实现了单一补偿电容故障诊断;文献[3]通过拟合实际故障数据,采用启发式准则,实现轨道电路组合故障诊断;文献[4-5]采用神经网络实现了调谐单元故障诊断;文献[6]将定性趋势分析的方法应用于调谐单元故障诊断。综合分析以上各文献,多是将补偿电容故障和调谐区故障分别进行研究,鲜有考虑补偿电容与调谐单元组合故障的复杂情况,且一些智能算法的应用导致诊断过程过于繁琐,运算效率很低。因此,本文从轨道电路故障诊断的实际需求和可操作性的角度,针对补偿电容与调谐区组合故障类型,提出一种基于变分模态分解(Variational Mode Decomposition,VMD)的ZPW-2000A型 无绝缘轨道电路故障特征提取方法,对补偿电容和调谐区组合故障的类型进行特征提取。该研究结果可以为诊断轨道电路复杂故障类型提供可靠的基础依据。
1 轨道电路建模与组合故障类型分析
1.1 ZPW-2000A型无绝缘轨道电路模型
ZPW-2000A型无绝缘轨道电路主要由钢轨、钢轨间的补偿电容、发送器、传输电缆设备、调谐区以及接收器等设备组成。其中,补偿电容等间隔布置在主轨道电路上,用来平衡高频信号在钢轨上产生的高感抗。调谐区内的调谐单元BA1、BA2和空心线圈SVA同载频的谐振关系,实现相邻轨道电路的电气隔离。在信号的传输方面,可以不考虑设备内部的元件及连接情况,只分析端子连接处的输入、输出电流与电压,从而可将无绝缘轨道电路等效为发送端、钢轨线路和接收端四端网络级联而成,其分路状态模型见图1。
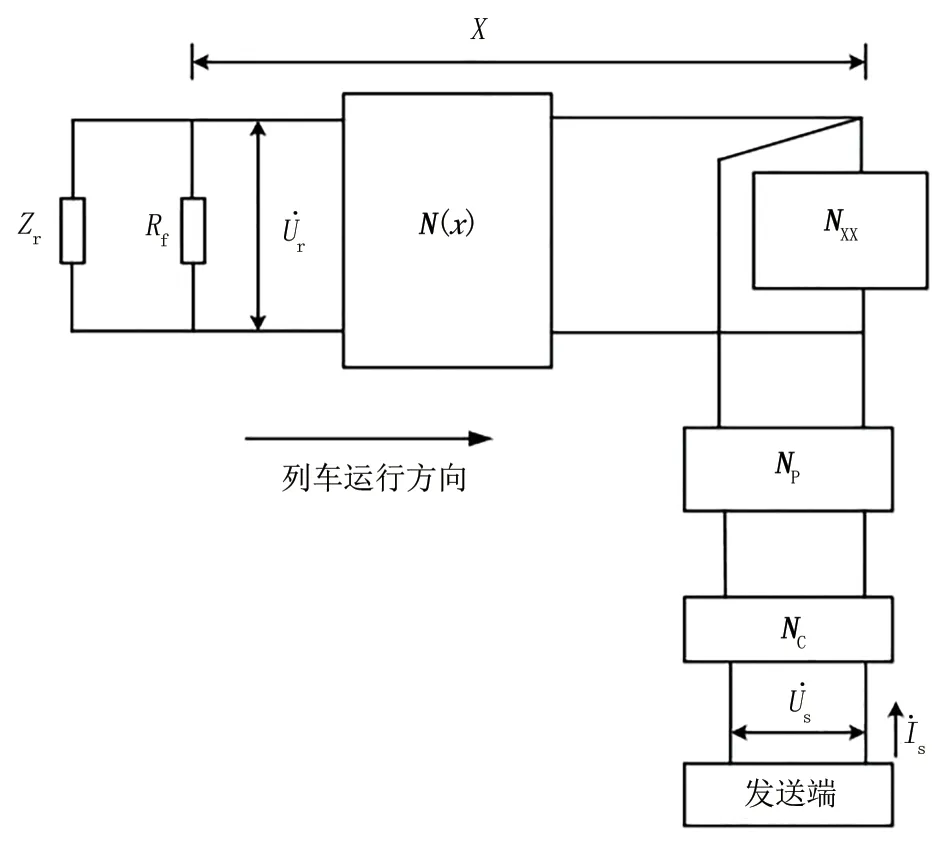
图1 无绝缘轨道电路分路状态四端网络等效模型
图1 中,Zr为从分路点向接收端看去的等效阻抗;Rf为列车车轮分路等效阻抗;Nc为传输电缆的等效四端网络模型;Np为匹配变压器的等效四端网络模型;Nxx为发送端调谐区正常时等效四端网络矩阵;N(x)为主轨道电路等效四端 网 络 矩 阵;U̇r为 接 收 端 电 压;U̇s为 发 送 端电压。
将建立的ZPW-2000A型无绝缘轨道电路各部分的模型进行级联,令分路点到发送端的传输特性等效四端网络矩阵F为
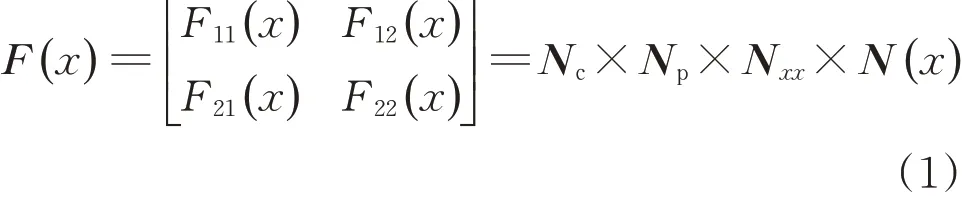
根据四端网络理论,端口电流和电压关系满足的矩阵关系为
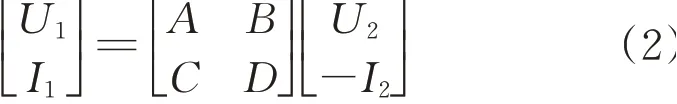
因此,轨道电路分路电流幅值包络函数表达式为
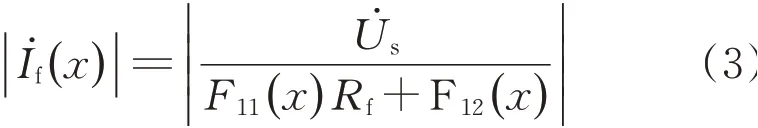
1.2 组合故障分路电流曲线
补偿电容的故障主要表现为容值降低和断线2种类型。分路状态下,补偿电容故障会导致信号设备错误动作,危及行车安全;调整状态下,补偿电容故障将造成“红光带”,降低行车效率。调谐区内设备的故障主要表现为线路连接松动和断线,将会破坏无绝缘轨道电路的电气绝缘性,导致信号的越区传输。本文重点以补偿电容故障和调谐单元故障、补偿电容故障和空心线圈故障2种复杂组合故障类型为例,进行分析。
1)补偿电容断线与BA2断线时,单独及组合故障分路电流归一化曲线见图2。当补偿电容C6和BA2同时发生故障时,分路电流曲线变得比较复杂,数值上整体小于轨道电路正常分路电流曲线;补偿电容C6的故障,导致C1~C6间的分路电流曲线发生显著变化;BA2的断线,导致靠近发送端的C9~C11间分路电流趋势改变。
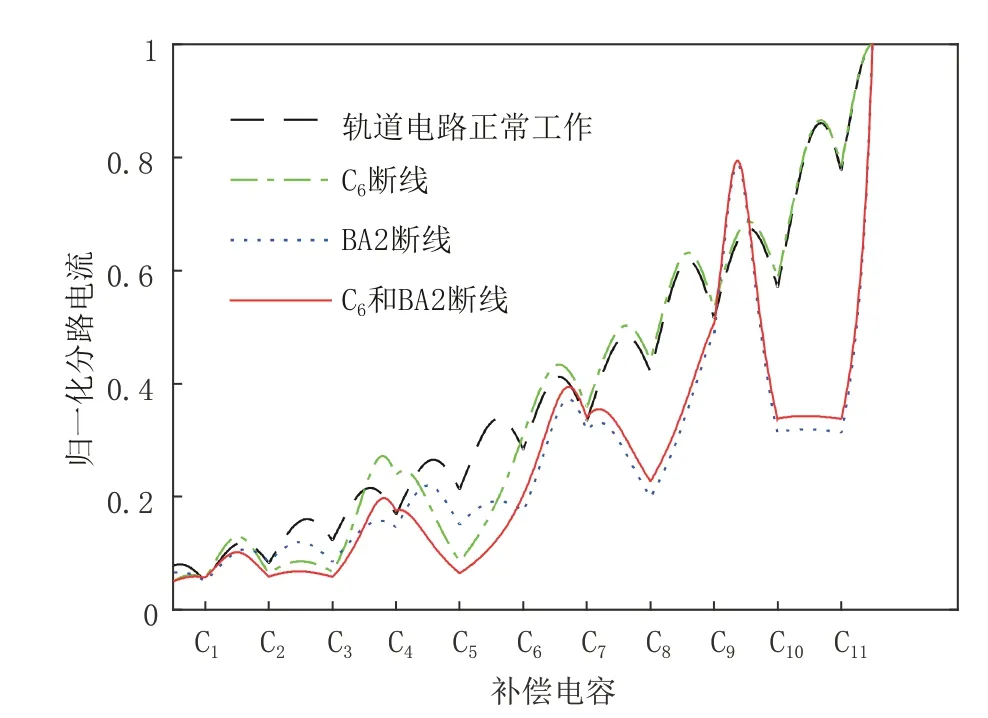
图2 补偿电容C6和BA2单独及组合故障曲线
2)补偿电容断线与SVA断线时,单独及组合故障分路电流归一化曲线见图3。当补偿电容C4和SVA同时故障时,C1~C4间的分路电流曲线趋势改变;C5~C8间的分路电流趋势与正常分路电流相同;SVA断线的影响与BA1断线类似,均为导致靠近发送端的3个补偿电容内分路电流曲线发生变化,但是趋势变化不完全相同。
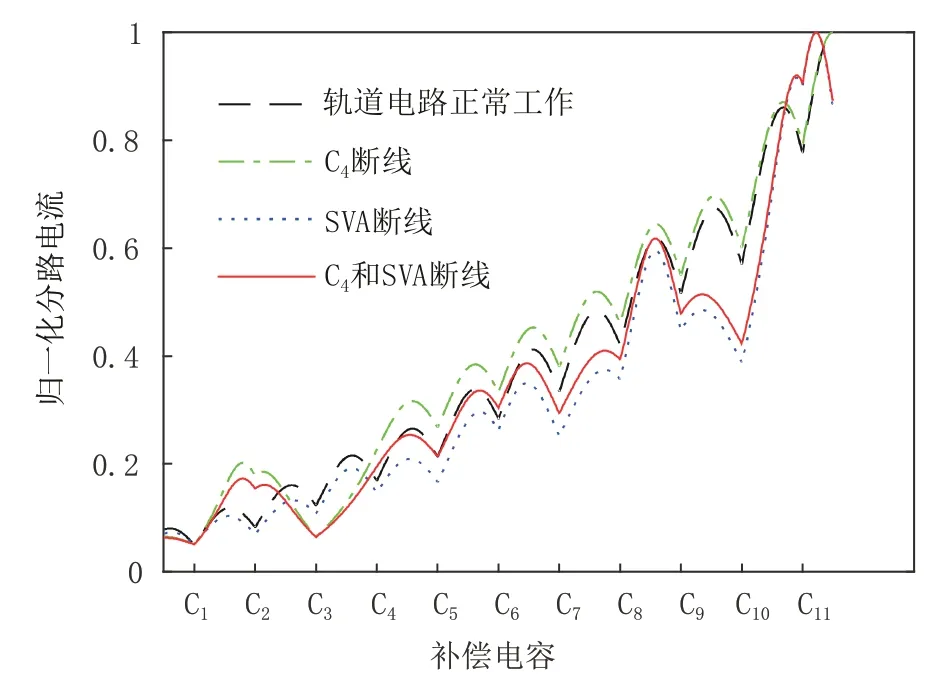
图3 补偿电容C4和SVA单独及组合故障曲线
2 VMD算法分析
VMD是一种新型完全非递归、自适应的模态分解和信号频域划分方法,具有精度高、噪声鲁棒性强的特点[7]。它避免了传统经验模态分解(Empirical Mode Decomposition,EMD)方法因循环递归分解导致的端点效应和模态混叠问题,有效提高了非线性强、复杂度高的时间序列的平稳性,是一种广受关注的信号分解方法[8]。采用VMD算法对ZPW-2000A型无绝缘轨道电路在复杂故障状态下的分路电流信号进行分解,可以得到一组本征模态函数(Intrinsic Mode Function,IMF)子信号,这些子信号波动相对平稳,且包含着多个不同的频率尺度,代表了不同的轨道电路故障特征。
VMD算法流程如下。
1)采用Hilbert变换,计算给定函数uk,获取其单侧频谱:
2)将uk与其对应的中心频率指数混叠,使其频谱转移到相应基带中。
3)根据高斯平滑度和梯度平方范数估计信号带宽。
4)得到约束变分问题为
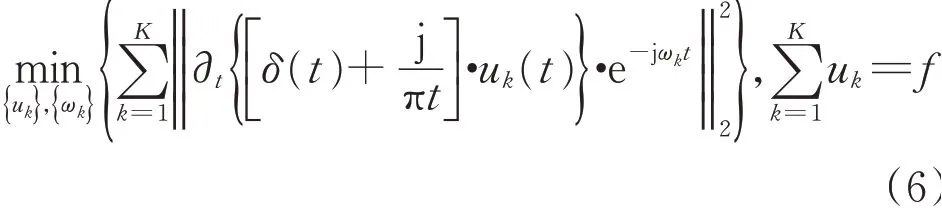
式中:uk={u1,u2,…,uk}为模态函数;ωk={ω1,ω2,…,ωk}为各个模态函数对应的中心频率。
为了将约束变分问题转成非约束变分问题,引入拉格朗日算子λ(t)实现精确重构,二次惩罚因子α实现重构信号的保真,两者结合后,得到拓展的拉格朗日表达式为
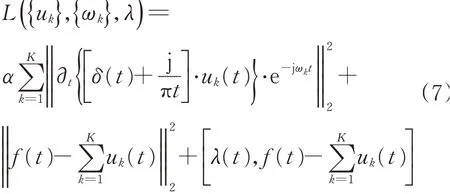
使用乘法算子交替方向法求解变分问题,迭代优化uk+1、ωk+1、λk+1,求解式(7),其最优解对应的模态分量为
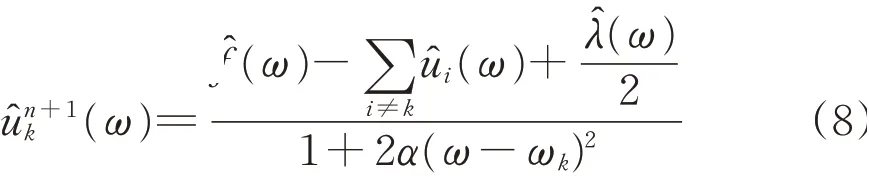
中心频率的更新算式为
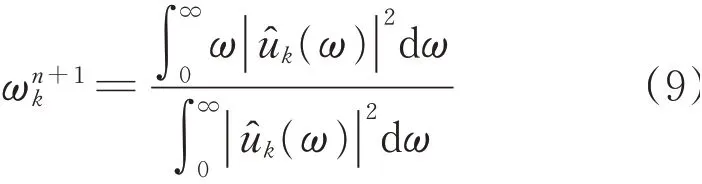
VMD算法迭代步骤[9]为
Step 1:初始化u1、ω1、λ1,n=0;
Step 2:令n=n+1,执行循环,更新uk;
Step 3:对所有ω≥0,使
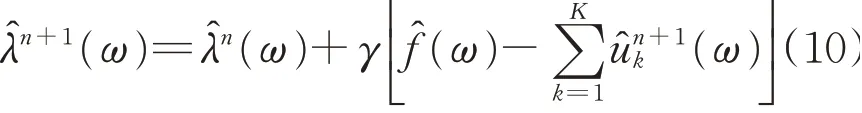
Step 4:重复Step2、Step3直至满足约束
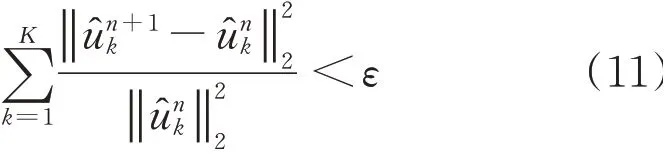
各个本征模态函数IMF的中心频率和带宽在迭代求解变分模型中不断地更新,直至满足迭代终止条件,得到K个IMF字信号,完成信号的自适应分解,有效避免了信号的模态混叠现象。
3 故障特征提取
与正常信号分路电流曲线不同,轨道电路分路电流故障信号被VMD分解后,不同频带的能量分布会发生较大的变化,而能量的变化包含着不同的故障信息。本文通过提取故障信号经分解后的各频带信号能量作为故障特征。
故障信号经VMD分解后,以不同频带信号的平方和作为能量特征[10],则在第i个频带内对应的能量值为式中:uk为第k个分解信号。

对式(12)做归一化处理,得到

式中:N为分解后的信号个数。
提取的信号能量特征向量集为
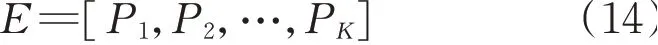
4 方法应用分析
为了检验基于VMD分解方法对轨道电路复杂故障特征量提取的有效性,以图3中补偿电容C6和调谐单元BA2同时断线时的分路电流曲线为例。首先采用VMD对正常状态下分路电流曲线进行分解,然后对故障状态下分路电流信号曲线进行分解,以便两者的相互对比,选取VMD分解的子模态数K=4,得到的分解结果见图4。
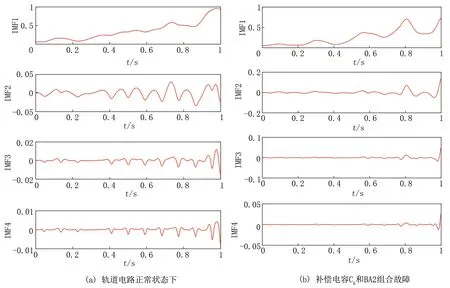
图4 VMD分解结果
对比图4中(a)和(b)可知,当轨道电路发生故障时,分路电流信号经VMD分解后的一系列子信号包含了不同时间尺度下的故障特征,避免了分解信号的模态混叠现象,提高了计算效率。分解后的故障信号出现了奇异波动,故障区域的起点和终点都出现了比较明显的尖峰波动。VMD使轨道电路在正常工作状态下的分路电流信号变得平滑,使其故障点以尖峰的状态表现故障信息,这也验证了使用VMD对轨道电路分路电流信号分解是适用的。
为了提取VMD分解后信号分量的故障特征,将轨道电路正常工作状态和本文2种复杂故障状态下分路电流曲线进行分解,计算相应的特征向量,各个频段内的能量分布见图5,具体的能量特征值见表1。
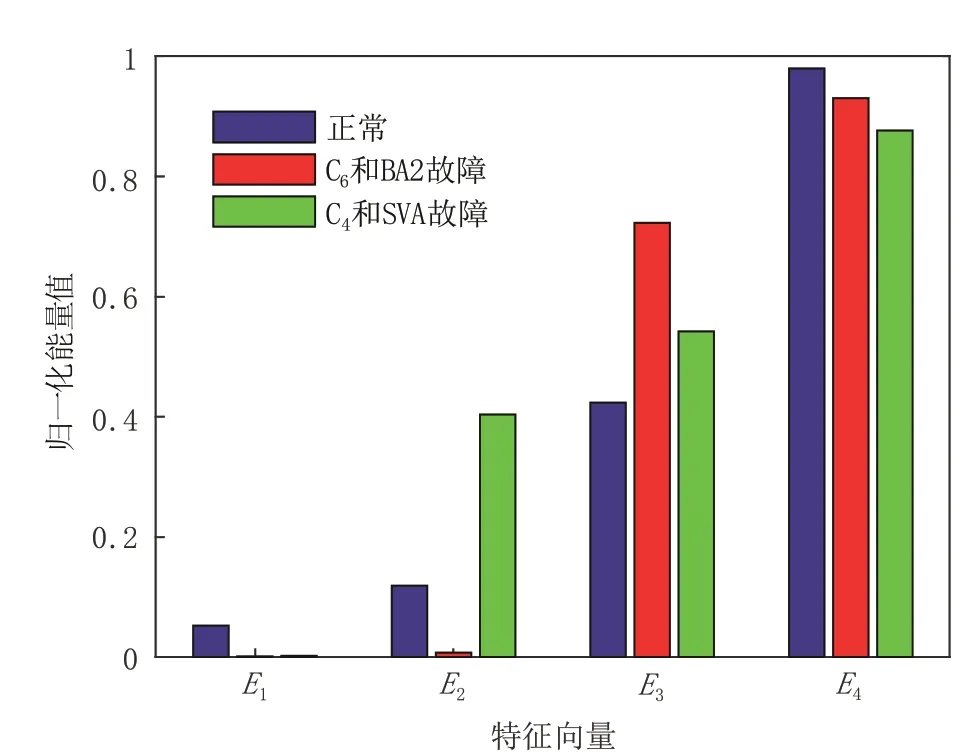
图5 VMD分解IMF能量特征分布

表1 VMD提取不同故障类型下的特征向量
由图5和表1可知,与正常状态下轨道电路分路电流曲线相比,无绝缘轨道电路复杂故障分路电流分解后的能量分布存在明显差异,而能量分布特征的差异正是不同故障类型的特征,可以为ZPW-2000A型无绝缘轨道电路的故障诊断提供可靠的依据。
5 结论
轨道电路组合故障分路电流曲线变化明显,其中包含的故障信息更加复杂,利用VMD分解信号可以避免传统方法导致的模态混叠现象,分解获得的分量信号具有不同的能量分布特征。本文提出的故障特征提取方法,可以在分解信号较少的情况下获取较多的故障特征,有利于故障的准确诊断。

