高压模拟井筒传热特性分析及分段式加温控制研究

贾光政，张雪青，侯永强，刘宗正

(东北石油大学 机械科学与工程学院，黑龙江 大庆 163318)

随着国内外石油勘探的发展，深井、超深井不断增加[1]，对射孔器材的耐高温性能提出了更高的要求。开展将射孔器材置于与井下温度与压力相近的模拟井筒中进行耐高温高压实验，是研究和检测射孔器材性能的有效方法[2-3]。由于模拟井筒多层介质的复合传热以及超高压工艺的特殊性，模拟井筒的温度控制十分复杂[4]，对模拟井筒传热过程进行建模与计算分析，能够提供高精度控制方案，也可为模拟井筒的设计与操作提供指导[5]。刘翠玲等以一维非稳态模型对高压釜及内部液压油的传热过程建立了数学模型，进行较准确的动态仿真，但并没有对内部射孔器材进行分析[6]；李娜等利用常减压装置稳态模型进行多目标优化，有效解决了多决策变量的选择，但其模型只适用于稳态条件[7]。本文应用一维圆柱体非稳态导热方程建立了高温高压模拟井筒及内部射孔器材的数学模型，应用当量等效导热来代替釜内液体传热过程，并利用有限差分法求解非稳态传热方程，以此对模拟井筒加热过程进行传热仿真。应用分段式加热模型，通过设定约束条件和目标，可实现不同需求的加热方案选择，为实际生产中模拟井筒加温控制方案设计提供参考。

1 系统构成

高压模拟井筒加热装置采用井式加热炉加热方式。电阻丝作为电热转换元件被布置于搁丝砖上，搁丝砖均匀布置在固定于加热炉内壁上的耐热金属架上。加热炉采用风机内部循环方式，使热空气进行强制流动，以保持炉腔内的温度均匀。高压模拟井筒安置在井式加热炉内，为射孔器材实验提供高温高压的环境。模拟井筒材料为铬镍钢；井筒内充入水或导热油；射孔器材材料为铬锰钢。高压模拟井筒加热系统组成如图1所示。

图1 模拟井筒加热系统组成

2 高压模拟井筒传物理模型

高压模拟井筒的简化模型如图2所示，其结构为中空圆柱体结构，模拟井筒尺寸参数如表1所示。

表1 模拟井筒尺寸参数 m

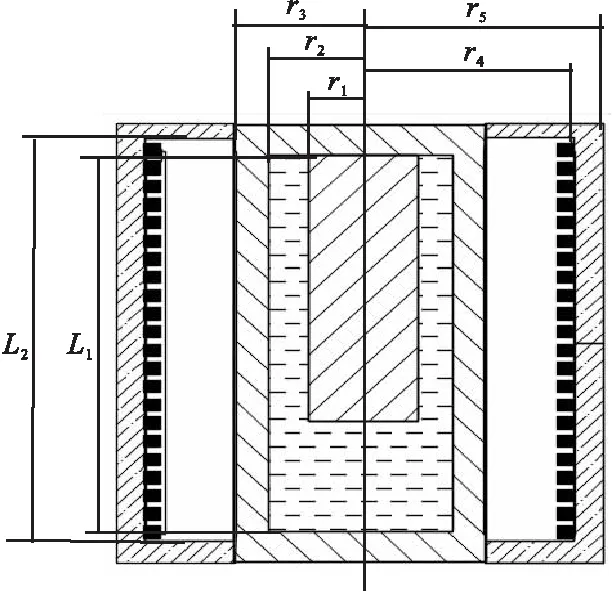
图2 模拟井筒物理模型

在加热过程中，模拟井筒各处的温度随时间而变化，建立数学模型时按非稳态导热建模。模拟井筒内部传热是轴对称的且轴向温度梯度远小于径向温度梯度，故模拟井筒及射孔器材的轴向传热可以忽略，可以采用一维圆柱体非稳态导热描述其传热过程。模拟井筒与射孔器材间的工作介质为有限空间内的对流传热，但由于间隙很小，此过程可以用等效导热过程代替。

3 数学模型与数值求解

3.1 模拟井筒及射孔器材传热方程

模拟井筒和射孔器材均为圆筒壁结构，传热过程沿中心轴对称相等，可近似为一维圆柱非稳态导热计算[1]，模拟井筒外壁到内腔及射孔器材内部各个节点处的能量方程为

(1)

式中：a为热扩散率，分别对应模拟井筒(r3≤r≤r2)与射孔器材(0≤r≤r1)的热扩散率，m2/s；τ为时间的步长，s；r为距离步长，m；r1为射孔器材外壁半径，m；r2为模拟井筒的内腔半径，m；r3为模拟井筒外壁半径，m。

3.2 模拟井筒的节点划分

将模拟井筒按一定截距划分等温网。Δτ为时间步长取5 s，Δr为距离步长取0.01 m。设炉腔内热空气温度为Tf1，高压模拟井筒部分的温度为Tw1，划分成18个节点；射孔器材部分的温度为Tw2，划分成17个节点。具体节点分布如图3所示。

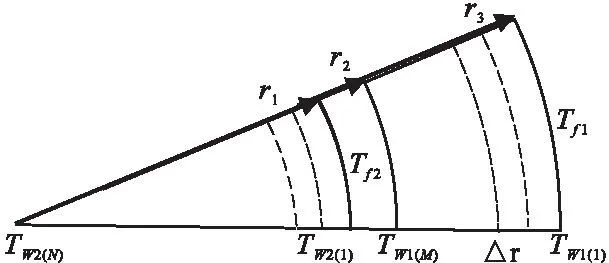
图3 模拟井筒节点分布

3.3 传热方程的数值求解

对于非稳态导热的数学模型，用解析法求解困难，需要构建离散化仿真模型进行数值求解[8]。将式(1)应用差分法，得到差分形式的方程为

(2)

4 初始条件与边界条件

4.1 初始条件

初始时刻，模拟井筒各处温度均为室温20 ℃，即

τ=0时，Tw1=20 ℃，Tw2=20 ℃，Tf2=20 ℃

4.2 模拟井筒外壁的边界条件

加热空气与模拟井筒外壁处的热流密度相等，其边界条件的差分格式为

(3)

其中h1为釜体外表面与加热空气的对流换热系数，可由炉腔内空气强制对流换热准则关联式得出：

(4)

式中：r4为加热炉内腔半径，m；Nu为对流换热的努塞尔数，无量纲。

根据气体强制对流实验关联式可计算努赛尔数Nu的数值[9]：

(5)

式中：Re为釜内气体的雷诺数，无量纲；Pr为空气的普朗特数，无量纲。

4.3 射孔器材外壁的边界条件

模拟井筒内液体的传热为有限空间内自然对流传热，因最小间隙为10 mm，相对较小，故仅计算液体传递的热流密度。假设通过射孔器材外壁表面热流密度与液体传递的热流密度相等，作为模拟井筒内壁与射孔器材外壁耦合的条件[10]。

(6)

式中：λw2为射孔器材的导热率，W/(m·K)；Tw2为射孔器材温度，℃；ql为通过液体的热流密度，W/m2。

引入当量导热系数λe，把自然对流传热过程作为相当的导热过程计算[11]。为表示流体的流动情况，引入格拉晓夫数Gr。Gr数是流体动力学和热传递中的无量纲数，其近似于作用在流体上的浮力与黏性力的比率。格拉晓夫数和流体普朗特数的乘积GrPr可以表示釜内流体的动量、能量及流动情况，因此常用来判断不同经验公式的适用范围。经计算，在20～400 ℃的工况下GrPr在6 000～106[12]，则根据经验公式，当量导热系数为[13]

λe=0.11(GrPr)0.29λf2

(7)

式中：λf2为水的导热率，W/(m·K)；λe为夹层的当量导热系数，W/(m·K)；Gr为流体的格拉晓夫数，无量纲；Pr为流体的普朗特数，无量纲。

同心圆筒夹层的热流密度ql差分方程格式为

(8)

式(6)为射孔器材外壁的边界条件，其差分方程形式为

(9)

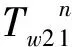
4.4 射孔器材中心的边界条件

射孔器材中心处近乎没有热量传递，故其中心节点处的热通量为0[14]：

(10)

将式(10)带入中心节点处的二阶中心差分为

(11)

将式(10)、式(11)代入式(1)中，则宽为0.5Δr的射孔器材中心区间的边界条件为

(12)

5 模拟井筒加热特性分析

将加热时间作为自变量，得出射孔器材的温度随时间变化曲线。并依次改变加热温度，得到在不同加热温度下的待检测器材中心温度随时间变化曲线，如图4所示。

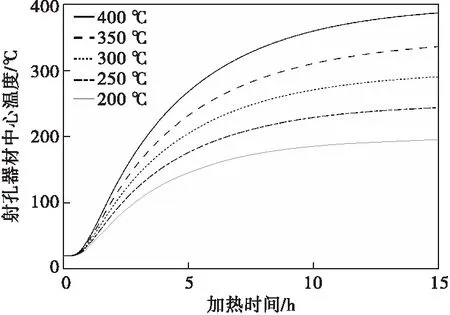
图4 射孔器材中心温度随时间变化曲线

图4中曲线加热温度从下到上依次为200、250、300、350、400 ℃。在加温初始约1 h内，曲线斜率较为平缓，意味着在这段时间内射孔器材中心温度几乎没有变化。这是由于温度的传递有滞后性，将热量从高压釜外壁传递到射孔器材中心是需要一定时间的，曲线保持平稳的时间即为热量传递到器材中心所需的时间。在加温初期约2～7 h，加热时间随加热温度变化，曲线以较高斜率上升，温度大幅上涨。这是由于此时内外温差较大，产生较大的温度梯度，更容易传递热量，因此升温速率较快。且加热温度越高，曲线上升斜率越大，温度传递得越快。7 h之后，升温速度明显变慢，当射孔器材中心温度越接近加热温度，升温速率越慢，曲线越平缓。

为探讨在不同的加热温度的条件下，模拟井筒向内部传热的能力随加热时间的变化。取模拟井筒外壁上的节点传递到下一个相邻节点单位面积的传热量，即热流密度作为衡量其传热能力的标准。外壁界面上的节点与其内部相邻节点间传递的热流密度为

(13)

由于Δr为定值，由此可知q12的取值与两节点的温差和模拟井筒的导热系数成正相关。将式(13)带入建立的传热模型中，得出q12随加热时间变化的曲线。并依次改变加热炉的加热温度，得出曲线如图5所示。

图5 不同加热温度下模拟井筒导热能力随时间变化曲线

图5中的多条曲线从下到上加热温度依次为200、250、300、350、400 ℃。通过模拟井筒外壁边界向内传递的热流密度随加热时间从零开始急速增长，约在1 h之内达到最大值，此时模拟井筒传热效率最高，且加热温度越高，其热流密度所达到的幅值越大。随后热流密度开始快速下降，并在5 h左右曲线出现拐点，下降速度放缓并逐渐趋于最小值，此时模拟井筒各处温度趋于均匀，且不同加热温度的热流密度相近。

6 模拟井筒分段式加温控制

在实际进行模拟井筒升温中，需要以较快速度达到目标温度，并且待检器材的温度要稳定在目标温度一段时间，以进行射孔器材的检测实验。由图4可知加热温度比目标温度高出的越多，加热到目标温度所需的时间越短。但由于温度的传递是有滞后性的，热量传递是一个较缓慢的过程，持续用较高温度加热很容易出现过度加热的现象，对检测器材容易产生负面影响，持续的高温加热也浪费了大量电量。因此，为了达到更好的加热效果，加热温度应该在加热过程中进行调控。模拟井筒加热是一个较复杂的过程，难以用一个固定的公式或程序进行加热温度的给定[15]。通过建立的高温高压模拟井筒传热过程的数学模型，并以此为基础进行分段式调温控制方案设计，从而得到能够满足生产实践要求的加热控制效果。

6.1 分段加温控制方案设计

采用分段式调温法进行加热，分三次逐步降低设定温度的方式，可以使升温曲线较为平稳，各部分温度相对均匀，最大限度地保证实验环境的稳定性和实验器材的安全。三个阶段的加热温度依次为T1、T2、T3，目标温度设置为T0。加热初期以较高温度加热，在射孔器材温度达到0.65T0时，下调加热设定温度；当射孔器材温度达到0.9T0时，再次下调加热设定温度；直至器材温度达到目标温度。

为探究不同加热温度下分段式加热的效果，依次设置三个阶段的加热温度。以达到目标温度后一小时内，射孔器材温度与目标温度的最大差值ΔT(T1,T2,T3)不大于5 ℃作为加热方案是否可行的必要条件；以加热时间t(T1,T2,T3)最快为选取目标。加热方案需要在必要条件的基础上使加热时间最小，其控制流程图如图6所示。

图6 加温控制流程图

6.2 分段调温加热控制模拟

设定目标温度为200 ℃进行加热仿真模拟，第一段加热温度T1应比200 ℃高很多。故选择以20 ℃为变化量，从400 ℃降低到300 ℃(模拟井筒最大加热温度为400 ℃)，选取6个加热预选值(l=1～6)。

T1(l)=400-20(l-1)

(14)

第二阶段加热温度T2的温度值应在T1与T3之间，选择以20 ℃为变化量，从T1降低到220 ℃，选取mmax个加热预选值，为简化计算，T2的取值比T1高的部分舍去，故T2是受T1、m影响的函数，T1的值越大，T2的预选温度越多。

T2(l,m)=T1(l)-20m

(15)

T2的预选值序数m的最大取值受T1的影响，其最大值为

第三阶段加热温度T3，其温度应与目标温度相近，选择以5 ℃为变化量，从220 ℃降低到205 ℃，选取5个加热预选值(n=1～5)。

T3(n)=220-20(n-1)

(16)

将温度T1、T2、T3代入到加温流程中，得出在不同加热方案下，加热到200 ℃所需要的时间t(T1,T2,T3)，到达目标温度T0之后一小时内的最大温差ΔT(T1,T2,T3)。经仿真计算，所需时间最短的可行加热方案为第一阶段加热温度为400 ℃，第二阶段加热温度为300 ℃，第三阶段加热温度为305 ℃，将射孔器材中心温度加热到200 ℃所需4.31 h，升温曲线如图7所示。

图7 射孔器材中心温度随时间变化曲线

7 结 论

(1)建立了模拟井筒及射孔器材在加热过程中的一维传热物理模型与数学模型，能够高效地进行变参数传热物理过程的求解。

(2)对高压模拟井筒的传热过程进行了动态仿真，分析了模拟井筒及射孔器材在加热过程中温度场的变化特性。模拟井筒向内传热能力随时间推进呈现出一种抛物线型的趋势，前期以较快的速度达到最高的传热效率，随后逐渐下降并逐渐趋于最小值。

(3)对分段式加温控制方案进行了设计分析和控制模拟，以加热时间最小为目标，获得了较好的加温控制效果。