基于随机森林的复坡堤越浪量预测研究

胡原野，王收军，陈松贵，柳叶，王家伟，田昀艳

(1.天津理工大学 机电工程国家级实验教学示范中心，天津 300384；2.交通运输部天津水运工程科学研究院 港口水工建筑技术国家工程实验室，天津 300456)

1 引言

防波堤作为港口建设中一种重要的水工建筑，对保护堤后建筑起着重要的作用。越浪量是指波浪越过防波堤的水量，通常用单位宽度上每秒水体越过防波堤的水量来度量。越浪量是防波堤设计的重要指标，对堤后结构物和堤面的安全有直接的影响。复坡堤是最为常见的防波堤类型之一，相比于单坡堤，其结构更为复杂，越浪量的计算更为困难；且目前国内尚无规范可循。本文提出了一种有效精确的复坡堤越浪量估算方法，对防波堤设计及提高防波堤安全性具有重要的意义。

国内外学者在越浪量方面的研究都做了很多的工作。对越浪量估算方法的研究大体分为3类：经验公式法、数值模拟法和机器学习法。经验公式法主要是通过建立实验模型，对实验数据进行分析，然后总结出经验公式；数值模拟法利用计算机建立研究模型，结合有限元，通过数值计算的方法实现对问题的研究；机器学习法将训练样本数据植入到计算机中，通过机器学习算法来模拟人类学习的过程，以此来实现对新样本的预测。王红等[1]通过物理实验分析了单坡堤上不规则波越浪量的相关因子，并由建筑物形态和波浪特征来确定越浪量，其成果被《港口与航道水文规范》[2]采纳；范红霞[3]通过搜集多种防波堤类型资料，建立水槽物理实验，分析了各影响因素对越浪量的影响，并给出了一种计算越浪量的方法。陈国平等[4]通过物理实验分析了不规则波作用下的越浪量，并发现影响越浪量和波浪爬高的因素基本相同，从而提出了不规则波作用下越浪量计算公式。陈松贵等[5]和Liu等[6]通过水槽实验分别研究了规则波和不规则波作用下岛礁陡变地形上直立堤越浪规律，给出了平均越浪量的计算公式。Owen[7]在不考虑斜坡粗糙度的情况下，通过一系列实验推导出越浪量计算公式。van de Meer等[8]对斜坡堤越浪量做了大量的工作，综合考虑了防波堤参数和波浪参数的影响，提出了斜坡堤上平均越浪量公式，该公式被欧洲大多数国家使用。美国《海岸工程手册》中采用的就是Ward和Ahrens[9]通过实验计算的越浪量公式。舒叶华等[10]通过对复式结构海堤越浪量进行研究，比较了国内外常见的复式海堤的越浪量计算方法。Oliveira等[11]基于粒子有限元法（PFEM）建立了数值波浪水槽模型，模拟了不可渗透海堤的越浪过程，给出了一种求解越浪量的工具。关大玮[12]应用 FLOW-3D 建立了可模拟规则波和不规则波浪的三维数值水槽，并模拟了复坡堤上越浪过程，将结果与实验数据对比，吻合较好。董志等[13]采用数值模拟的方法，利用RANS方程和VOF法建立数值波浪水槽，针对复式海堤分别进行了规则波和不规则波越浪的数值模拟。而van Gent等[14]采用了人工神经网络的方法对越浪量做了预测，并给出越浪量在不同置信区间的值。Formentin等[15]在前人的基础上增加了模型的输入参数，对模型做了进一步的完善。刘诗学等[16]采用人工神经网络方法对单坡式防波堤越浪量做了估算Liu等[17]通过使用深水波参数作为输入开发了一种反向传播的人工神经网络模型，来预测珊瑚礁上不透水的垂直海堤的越浪量。传统的经验公式法通常需要消耗大量的人力、物力资源，且公式的推导过程较为繁琐；数值模拟法通常需要为了达到相应的精度，而需要非常大的计算量，对计算机性能要求较高；神经网络方法在经济效益方面具有一定优势，但是仍存在一些不足之处，比如全局参数搜索比较困难，对奇异样本敏感，容易陷入局部最优。

随机森林是近几年来兴起的一种基于统计学的人工智能算法。它基于决策树结构组成的强学习器，是一种集成学习算法，该算法对异常数据有较高的容忍性，且能够直接处理高维度样本[18]。目前，该方法极少应用于越浪量预测方面。本文提出利用随机森林算法预测越浪量，为越浪量的计算提供了一种新的方法。

2 数据获取与处理

2.1 CLASH 数据集介绍

“CLASH”是欧盟启动的一个项目计划，它搜集了各国有关越浪量的实验数据，组成了较为丰富的越浪量数据集。该数据集有1万多条数据，包含了多种防波堤类型，每条数据都包含波要素参数、越浪量和防波堤结构参数。此外，数据集包含有关实验可靠性和结构复杂性的一些信息，RF表示实验可靠性，取值在1～4之间，RF值越小说明实验可信度越高，相反则说明实验可靠性越低；CF表示断面的复杂度，取值在1～4之间，CF值越大表示断面越复杂，反之亦然。

2.2 数据处理

本文主要研究复坡堤越浪量，根据复坡堤的结构特点，选取以下参数：堤前有效波高Hm0,t、堤前谱周期Tm−1,0,t、 波浪入射角 β、堤前水深h、坡度m、堤脚浸没水深ht、 堤脚宽度Bt、护面块体粗糙度 γf、平台以下结构与水平面正切值 co tαd、平台宽度B、平台上水深hb、波浪爬高范围内的平均坡度（包含平台） c otαincl、护面块体的平均粒径D、堤顶高程Ac、 胸墙顶高程Rc、肩台宽度Gc。结构示意图如图1所示。

图1 复坡堤参数示意图Fig.1 Schematic diagram of composite slope breakwater parameters

数据处理是指对数据集进行筛选、整理，删除错误、无效和有缺失值的数据。经过一系列处理，将原始数据变为可供模型直接使用的数据。其方法如下：

（1）删除标签为 Non-core data 的数据；

（2）删除q<10−6m3/(s·m)的数据；

（3）删除有缺失值的数据；

（4）删除CF=4和RF=4的数据行。

经过对数据的处理，用于模型使用的数据量为2 462 条。

2.3 无量纲化

由于越浪量数据集是在特定的实验条件下测量的，会存在不同组次数据的比尺不同，为了消除实验模型比尺和数据量纲之间的差异，需要对数据进行无量纲化。对于每条数据，根据求出波长，然后按以下方法进行无量纲化：

（1）计算出Hm0,t/Lm−1,0,t；

（2）计算出h/Lm−1,0,t；

（3）水平方向参数除以波长；

（4）竖直方向参数除以波高；

（5）角度和地貌参数保持不变；

（6）越浪量采用EurOtop手册[18]中方法进行无量纲化，并对其进行归一化

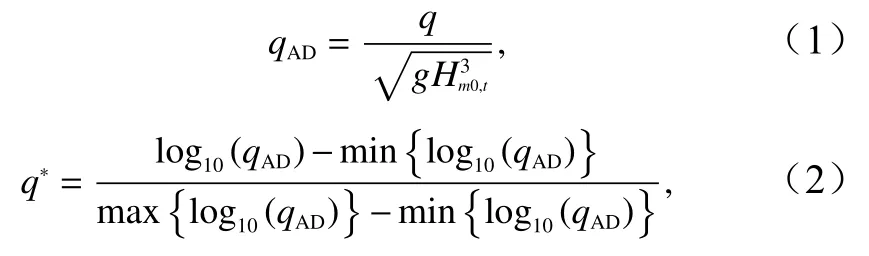
式中，q为越浪量 (m3/(s·m))；Hm0,t为堤前有效波高（m）；g为重力常量，取 9 .8 m/s2；qAD为无量纲化后的越浪量(m3/(s·m))；q∗为归一化后的越浪量 (m3/(s·m))。

3 随机森林算法

3.1 随机森林原理

随机森林是一种基于决策树模型的集成学习算法，通过对样本数据随机抽样组成多个不同的决策树，再把决策树计算结果通过某种组合策略来获得随机森林的预测结果。随机森林可以看作是决策树的整合择优。因此，随机森林通常比单纯的决策树模型具有更好的拟合能力，且随机森林在分类问题和回归问题上都具有较好的效果。本文建立的越浪量预测模 型就是随机森林在回归问题上的体现。

3.1.1 决策树

决策树是随机森林的基本组成单元，也是一种机器学习算法，它的建立过程基于树形结构，主要由内部节点、树枝和叶节点组成。如图2所示，最上面的是根节点，严格来说，根节点也属于内部节点。树的建立过程就是节点分化的过程，每一次节点划分都会得到对应的输出，即经过分化多了一个节点。经过有限次的条件划分结束后，最终每个单元的输出也就确定了，即叶节点。一般来说，随着模型复杂程度的提高，决策树也随之长得很大。

图2 决策树基本结构示意图Fig.2 Schematic diagram of the basic structure of the decision tree

决策树理论的核心就是如何最优地确定切分点。随着决策树的逐渐长大，样本划分的也越来越细，也就是各节点的样本纯度也会越高（即越来越趋于同一类）。每次逐步划分当前所有特征中的所有取值，然后基于平方误差最小化准则选择最优的切分点。比如切分点为训练集中第j个特征变量x(j)，且x(j)的值为s，定义区域和区域然后确定j和s，使得平方误差最小，即求解下式[19]

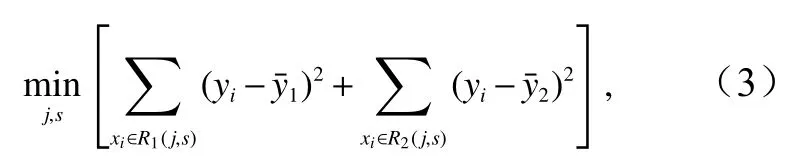
式中，yi为输出变量；为在区域R1上yi的均值；为在区域R2上yi的均值。

在确定出最优的 (j,s)后，该节点就会划分为两个子节点，然后对每个子节点重复上述过程，直到满足条件停止。

3.1.2 随机森林算法结构

随机森林是由一系列决策树组成的一种强学习器，根据Bagging集成方法来提高算法的精度。具体步骤如下：

（1）从越浪量样本集有放回地随机抽取n个训练集，原始样本集中会有约36.8%的样本未被抽到，把该部分数据称为袋外数据（OOB）。

（2）利用抽取的n个训练集组成n棵决策树，在分裂过程，其中在每一个内部节点从M个特征中随机选择m个特征进行分裂（M≥m）。这样通过特征的随机性增加了各决策树之间的差异性。

（3）经过训练，每一颗决策树都会对样本做出回归预测，分别得到n个预测结果q1，q2，q3，···，qn。

（4）采用平均法的方式，将n棵决策树的输出结果综合平均，最后得到预测结果q，即因此，基于随机森林的复坡堤越浪量预测模型结构如图3所示。

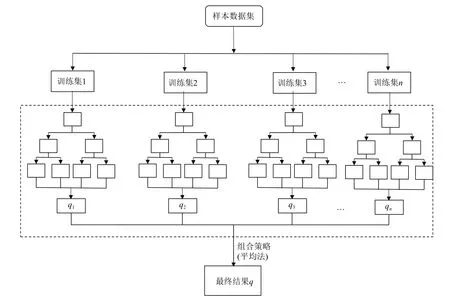
图3 基于随机森林的复坡堤越浪量预测模型结构图Fig.3 Structure diagram of overtopping prediction model of composite slope breakwater based on random forest

3.2 模型的建立

本文利用Python提供的Numpy和Pandas库对数据进行处理，使数据转化为可直接供模型使用的数据类型。利用Sklearn建立越浪量预测模型，把经过处理后的数据输入到建立的模型中。其中，将数据集随机地划分为两部分：90%作为训练集供模型学习，10%作为测试集用来评估模型的性能。表1为处理后的无量纲数据的分布特征。

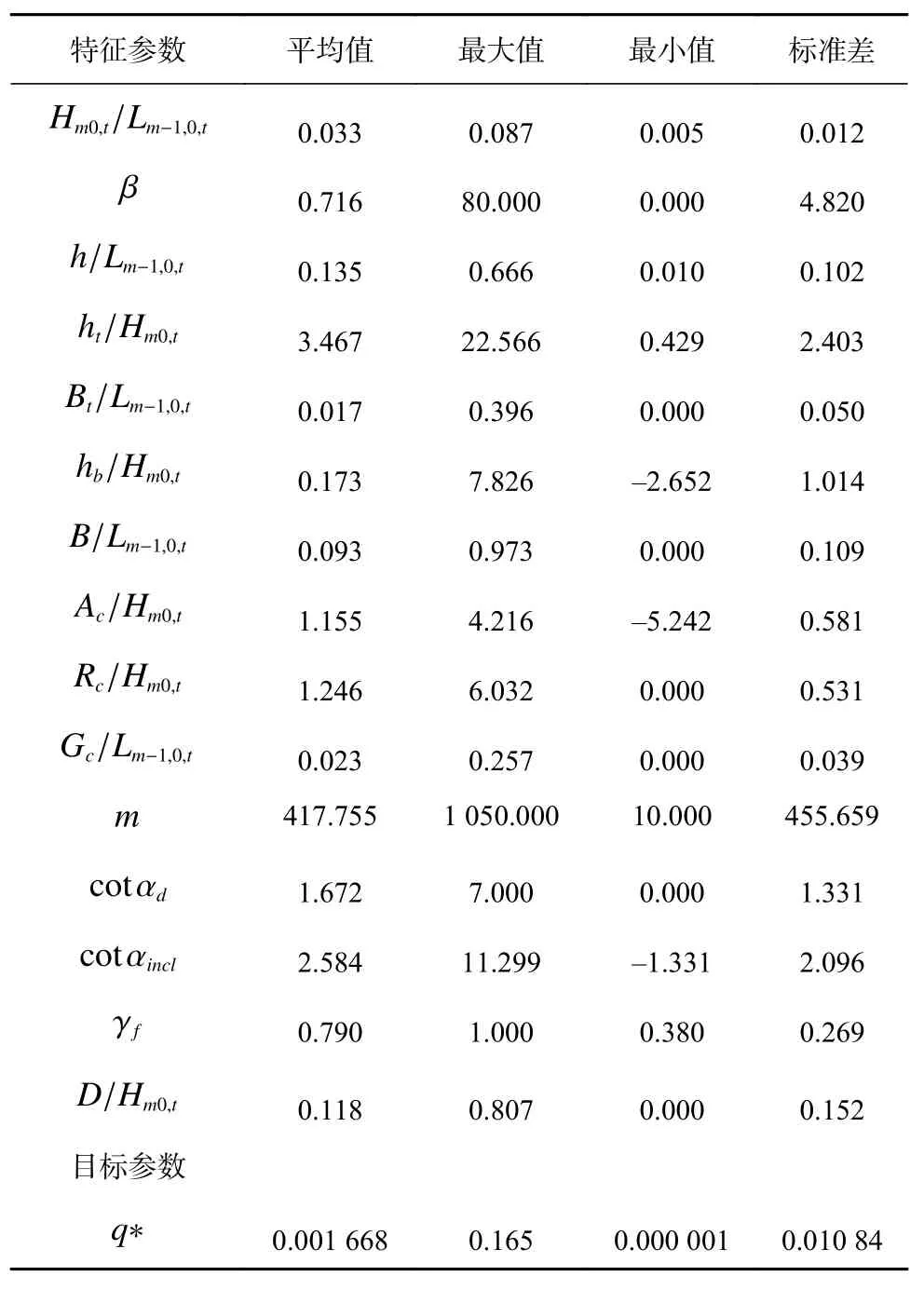
表1 无量纲化后输入参数分布特征Table 1 Distribution characteristics of input parameters after dimensionless

3.3 模型调参

模型参数的调节对模型性能有非常重要的影响，本文主要对影响随机森林精度较大的3个参数做优化，分别为决策树的数量（n_estimators）、决策树的最大深度（max_depth）和随机选择的最大特征数（max_features）。综合考虑模型精度和运行时间成本，给上述3个参数选取多个适当的值，取值范围如表2。

表2 重要参数取值范围Table 2 Value range of important parameters

其中，n_estimators的取值步长为10；max_depth的取值步长为5；max_features有两种取值：auto表示取所有的特征，sqrt表示取特征数的平方根。

本文利用Sklearn库中网格搜索（GridSearchCV）方法对3个参数进行调优，该方法只需把设置好范围的需要调优的参数输入到此算法中，它就会遍历整个范围获得多种参数组合，这样就能方便快捷得到最优的结果。经过网格搜索计算，得到的最优参数取值

4 结果分析

为了评估随机森林算法对越浪量的预测精度，通过比较预测值和真实值来直观判断。同时，通过R2(决定系数)来定量计算模型的预测精度,R2的值越接近1，则预测值和真实值越接近，表明模型越好；反之，R2越接近0，则表明模型越差。决定系数[20]计算公式为

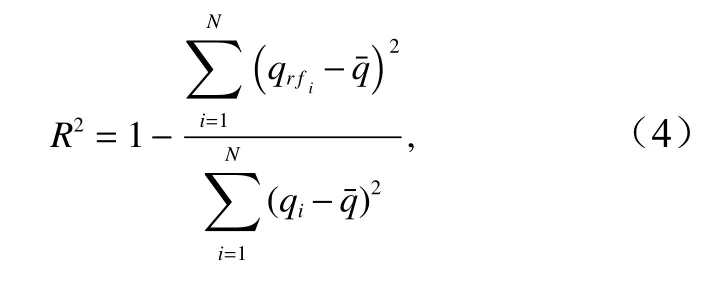
式中，N为样本数；qrfi为预测值（第i个 样本）；为真实值 的平均值；qi为 真实值（第i个样本）。

4.1 预测结果分析

将划分好的数据集输入到建立好的随机森林模型中，分别得到训练集和测试集的预测结果，如图4和图5。训练集预测结果表示模型对样本数据的学习能力，测试集的预测结果表示模型对测试数据的泛化能力，即对新样本的适应能力。

从图4和图5可以看出，训练集预测结果基本都在5倍误差区间内（两侧实线之间），且决定系数R2=98.8%，表明该模型具有很好的学习能力；测试集与训练集是完全不同的数据集，这部分并没有参与模型的训练，其结果依然能够基本上落在5倍误差区间内，且决定系数R2=92.7%，预测结果很可靠，表明模型对 新样本也具有很强的适应能力。

图4 训练集预测结果（随机森林）Fig.4 Prediction result of training set(random forest)

图5 测试集预测结果（随机森林）Fig.5 Prediction result of testing set(random forest)

4.2 与集成神经网络算法的对比

为了进一步验证随机森林算法预测复坡堤越浪量的精度，与集成神经网络算法预测结果做了对比采用与随机森林算法相同的数据集，建立了基于集成神经网络算法的越浪量预测模型。神经网络模型包含3层：输入层、隐含层和输出层。由于目前没有足够的理论确定神经元个数，常采用逐步试验法选择结果较好的，神经元个数最小的组，以免过拟合。因此最终确定输入层神经元数为15，隐含层神经元数为25，输出层神经元数为1。激活函数选择选取双曲正切函数（tanh），输入参数采用max-min归一化。构建100个网络模型，然后将这100个模型的输出结果通过平均的方法得到最终集成神经网络的输出结果。集成神经网络模型的预测结果如图6和图7所示，训练集大部分落在5倍误差范围内，也有比较多的点落在了5倍范围之外，决定系数R2=91.9%；而测试集的结果基本都落在5倍误差范围内，决定系数R2=87.7%对比两种算法训练集的预测结果（图4和图6）发现随机森林算法的结果明显比集成神经网络更集中在45°理想线附近（中间的实线），且决定系数也高于集成神经网络，这说明随机森林比集成神经网络具有更强的学习能力；对比两种算法的测试集结果（图5和图7），直观上不容易看出明显的差别，但根据两者的决定系数可知，随机森林依然要高于集成神经网络说明随机森林算法的泛化能力也更好。综上所述，不管是训练集还是测试集，本文建立的随机森林模型的准确度都要优于集成神经网络。这是由于在构建随机森林模型时，每棵决策树的训练集是通过Bagging集成方法抽样，且决策树分裂时采用随机选择，这使得随机森林中的决策树多样性增加，从而更好地发挥了集成思想的作用。

图6 训练集预测结果比较（集成神经网络）Fig.6 Prediction result of training set (ensemble neural network)

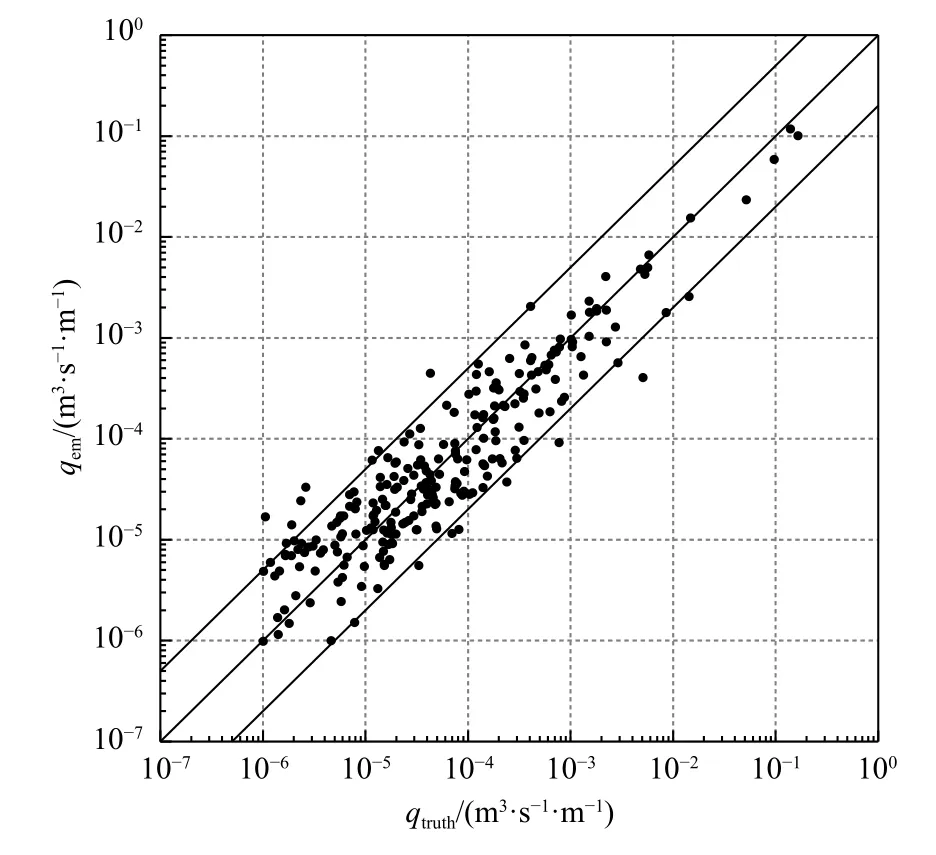
图7 测试集预测结果比较（集成神经网络）Fig.7 Prediction result of testing set (ensemble neural network)

4.3 特征参数对预测精度的影响

分析特征参数的重要性就是探究哪些特征对模型的影响大，哪些特征对模型的影响小，这样有助于更好的做特征筛选，即对于影响特别小的特征，对模型来说或许会被认为是噪点，可以选择丢弃。一方面，可以提高模型的精度；另一方面，利于减小模型的计算量，从而提高效率。

通过随机森林模型对越浪量预测的同时，模型可以评估所有输入特征对预测结果的重要性。其原理是：在建模过程中随机森林会挑选出某一个特征对其加入噪声，然后观测对计算结果的影响，最后比较各特征之间的影响大小。一般用袋外数据误差评价。方法是：对于一颗决策树，计算OOB的误差e1，对于特征参数Xi，置换OOB中的第Xi列，保持其他列不变，再次计算袋外误差e2，用e1−e2表示特征参数Xi的重要性。最后把所有决策树计算得到的e1−e2取平均，即特征参数Xi对随机森林模型的重要性。袋外误差e的计算公式为

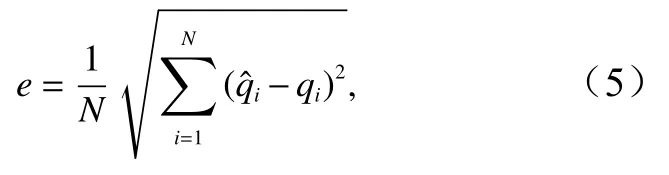
式中，、qi分别为第i个样本的预测值和真实值；N为对应的样本数。因此，特征参数Xi的重要性评分[21]为

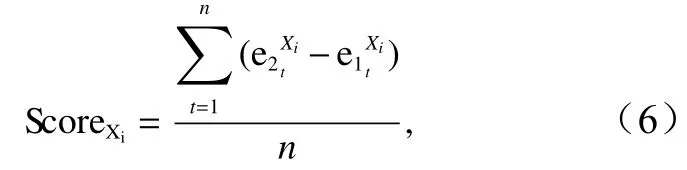
式中，n是随机森林中树的个数；表示特征参数Xi在置换之前的第t棵树的袋外误差；表示特征参数Xi在 置换后的第t棵树的袋外误差。如果对某个特征加入噪声，随机森林的袋外准确率大幅减小了，说明该特征的重要程度较高。通过随机森林算法对特征计算重要性评分，然后对其进行归一化后，就得到特征重要性。由于有些特征参数本身具有无量纲特性，且这类数据之间的差异较大，这里不予考虑。我们只讨论经过无量纲化后的特征对预测结果的影响，如图8。

图8 模型特征参数重要性评价Fig.8 Importance evaluation of model characteristic parameters

由图8可知，重要性最高的特征参数为墙顶高程Rc，其次是堤顶高程Ac和 平台上水深hb，再者是平台宽度B和波陡Hm0,t/Lm−1,0,t，而堤前水深h、堤脚浸没水深ht和肩台宽度Gc的重要性相当，护面块体平均粒径D和堤脚宽度Bt对预测结果的影响最小。不难理解，墙顶能够有效的阻挡波浪越过堤顶，随着墙顶高程的增加，波浪在挡浪墙处的破碎更加剧烈，大部分水体将被挡在海浪侧。需要消耗更多的能量波浪才能越过堤顶；倘若波浪超过堤顶，就会有比较大的可能发生越浪，堤顶高程的增加对减少越浪具有重要的意义；平台可以削减海侧方向来的波浪，而且设置在静水位附近时的削弱效果最好[22]，平台宽度一定程度上会影响波浪的爬高；波浪在堤脚附近时，由于浅水变形使得波陡变大最终发生破碎，导致波浪损失能量，因此会对越浪量造成一些影响；护面块体粒径大小主要是以渗透率和孔隙率的形式影响越浪量，对越浪量的影响不大；而堤脚宽度对越浪的影响非常小。

分析各特征对预测精度影响，从模型角度讲，可以对模型做特征选择，丢弃对预测精度影响小的特征，保留影响大的特征，来进一步提高模型的精度；从工程角度讲，了解影响越浪量大小的因素，有利于控制越浪量，为设计防波堤提供参考。

5 结论

本文以欧洲CLASH项目作为数据支撑，利用Python构建了基于随机森林算法的复坡堤越浪量预测模型并通过调参使模型得以优化，从而提高了模型的准确率。为了验证本文提出的越浪量预测模型的准确度，将本文建立的随机森林预测模型与集成神经网络模型的预测精度进行对比，结果显示，随机森林的预测精度要优于集成神经网络。此外，随机森林算法还给出了特征参数对模型预测精度的影响大小，为进一步对特征参数做筛选提供依据。通过本文的研究，实现了将随机森林算法应用于越浪量预测领域，为计算复坡堤越浪量提供了一种新的方法，对设计防波堤和提高防波堤安全性具有较大的实际应用价值。