解析四维集合变分参数优化方法研究

贾彬鹤，李威*，梁康壮*

(1.天津大学 海洋科学与技术学院，天津 300072)

1 引言

进行数值预报时，预报的准确率会随着预报时间的增长而迅速下降。造成这种现象的原因主要有3点：一是模式方程对物理过程的参数化方案有一定误差；二是数值预报模式的初始场有误差；三是数值预报的计算方法有一定的误差[1]。

为提高预报准确率，如何改进模式物理参数是需要解决的问题。数据同化方法可以从观测数据中提取有效信息，并修正数值模式误差。四维变分数据同化 （Four Dimensional Variational Data Assimilation，4DVar）方法能够把各个不同时刻的观测资料纳入统一的分析预报系统中，通过相应的切线性模式和伴随模式优化初值条件，并使各要素自然满足动力热力条件[2–3]。由于其较好的同化能力，众多学者也采用4DVar方法进行了模式参数优化的研究[4–7]。例如，Inazu等[8]将进化算法应用于区域海潮模型，优化了模型的边界条件和物理参数。Wang等[9]提出通过遗传算法和神经网络交替组合的方式来纠正系统参数误差。王云峰等[10]提出了一种新的利用观测资料来同时优化模式初始场和物理参数的扩展四维变分同化方法，并以Ekman边界层模式和Lorenz模型为例进行了数值试验。魏敏[1]采用4DVar方法，利用Lorenz模型和Hamilton方程，结合观测数据对该模型的参数进行了优化。然而，4DVar方法需要采用伴随模式，对于原数值模式需要编写与之相对应的特定的伴随模式，并且伴随复杂程度高、代码编辑量大，使得这种同化方法可移植性很差。另一方面，4DVar采用的静态背景误差协方差矩阵不具有流依赖特性，限制了四维变分的同化能力。

序列同化方法如集合卡尔曼滤波（Ensemble Kalman Filter，EnKF）能在避免伴随的同时产生流依赖的背景误差协方差矩阵。为结合两种方法的优点，可以在变分框架下引入集合状态变量，从而产生四维集合变 分 （Four Dimensional Ensemble Variational Data Assimilation，4DEnVar）。最初，Liu 等[11]将四维变分增量优化方法与集合方法结合提出了该方法，但将其命名为集合四维变分数据同化方法（Ensemble Four Dimensional Variational Data Assimilation， En4DVar） ， 并采用一维浅水模型对该方法进行了验证。随后，Liu等[12]设计了局地化方法，采用高等天气研究与预报（ARW-WRF）模型，设计了观测系统模拟试验，并检验了它们在实际数据同化中的性能，证实了4DEnVar局地化技术可以有效地减轻采样误差对分析的影响。根据世界气象组织（WMO）会议建议，Liu和Xiao[13将En4DVar更名为4DEnVar，以便将4DEnVar和使用伴随模型的En4DVar区分开来。4DEnVar 方法在业务化系统中也有所应用。Arbogast等[14]对四维轨迹的输入和存储等问题，提出了一种具有分布式输入和存储扰动的四维集合变分集成并行实现办法。Yang和Mémin[15]探索了一个动力学公式，该公式允许在一个大规模的流动模型中同化高分辨率的数据，并将该原理结合4DEnVar技术来估计随机浅水模型的流动初始条件和非均匀时变子网格参数。Song和Kang[16]采用混合四维集合变分方法（hybrid-4DEnVar），改进了北半球500 hPa夏季月位势高度预报。杨雨轩[17]利用WRF模型研究了POD-4DEnVar和传统三维变分方 法 （Three Dimensional Variational Data Assimilation 3DVar）对华南暴雨的模拟效果，并研究了物理集合方案对4DEnVar的影响。

4DEnVar可以构造多个能反映出背景误差协方差分布特征的样本形成集合，为变分同化系统提供流依赖背景误差协方差估计。然而，需要指明的是Liu等[11]将集合成员扰动关于集合均值展开来构造的协方差矩阵，反映了集合的统计性质，而非误差的传播性质。在线性模型下，这两种协方差矩阵等价，但对于非线性模型则不然。此外，目前4DEnVar方法研究集中在初始场的优化，尚未有进行参数优化的研究。为此，本文提出了专门进行模式参数优化的解析四维集合变分数据同化（Analytical Four Dimensional Ensemble Variational Data Assimilation， A-4DEnVar） 方法，该方法在4DVar框架下，将集合样本扰动关于迭代生成的模式参数处展开，有效刻画了误差在非线性模型下的传播方式，避免了伴随模式的使用。在此基础上，进一步求得代价函数梯度为0的解析解，能迅速得到代价函数极小值，完成模式参数优化。本文采用 Lorenz-63 模型[18]通过 4DVar与 A-4DEnVar 方法进行参数优化孪生试验和敏感性试验，证实算法的有效性。

2 解析四维集合变分参数优化方法

假设动力系统为

式中，Xi−1为第 (i−1)时刻的状态变量；Xi为 第i时刻的状态变量；M(i−1)→i为从时刻 (i−1)到时刻i的演化算符；M(i−1)→i中包含了有偏差的模式参数 Λ。按照式（1）可以递推得到如下方程

假设初始场X0与驱动场Fi都是准确的，唯一不准确的是模式参数 Λ，在 Λ上叠加一个小扰动 λ˜得到另外的一个模式参数为可以预期，只要积分步长不是很长，受新的模式参数 λ影响，各个时刻状态变量可以表示为原状态变量Xi与扰动量相加的形式Xi+则可以得到扰动量所满足的方程

和

于是演化公式可改为

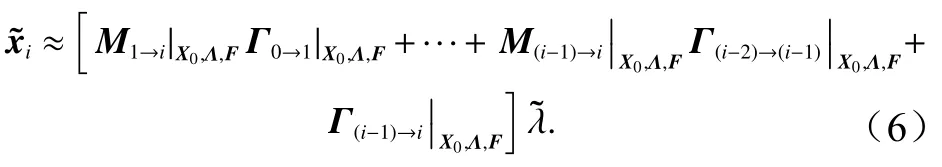
注意到，此处假设初始场和外界强迫场都是准确的，即初始场和外界强迫场都不扰动，在这种情况下，状态变量的扰动都来自于模式参数的扰动。

定义广义背景场误差协方差矩阵为

式中，矩阵实际上包含了切线性演化算符，其转置矩阵则包含了伴随算符信息，于是，

如果只通过扰动参数构造集合，则可以在最小二乘意义下，显式地求解出式（7）矩阵的具体形式，即

如果只优化模式参数，则四维变分的目标函数为

式中，Yi为第i时刻的观测；Hi为第i时刻的观测投影算符；Ri为第i时刻的观测误差协方差矩阵。

传统四维变分对模式参数进行最优估计的时候，就是将目标函数对模式参数 Λ求梯度，并将目标函数值和梯度值代入到最优化算法中，通过线性搜索和逐步迭代得到最优的模式参数。仿照这一过程，在当前模式参数 Λ附近进行扰动展开，推导 Λ附近使得目标函数取极小值的最优扰动量，设扰动量为δΛ，将在当前模式参数 Λ 附近进行展开，由于扰动量是小量，忽略高阶项后，可以得到

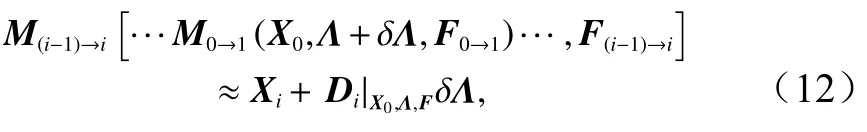
将式（12）代入式（10），则四维变分目标函数为

接着求出式（13）中目标函数相对于扰动量δΛ的梯度，

令式（14）梯度为0，即∇J(δΛ)=0，则可以求出δΛ的解析表达式

需要指出的是，这一最优增量是在 Λ为初猜场的情况下得到的，对于非线性动力系统，只要稍微有一点改动，上述最优增量的值就必然会发生变化。因此，为了让这一方法具有一定的稳定性，需要仿照传统四维变分的做法，引入线性搜索过程，即在相空间的δΛ方向上，以一定的步长 β线性搜索（例如采用二分法）使得目标函数在该方向上取极小的最优值 β ·δΛ作为订正量的最优取值，将 Λ +β·δΛ作为下一次迭代的猜测值代入目标函数，继续计算解析解，循环往复上述过程从而获得最优的模式参数。

3 数值试验

1963年美国麻省理工学院的气象学家Lorenz在对天气预报动力学模型进行数值计算时，发现了一个由非线性微分方程组所描述的著名的 Lorenz方程[18]该方程是一个3个变量模型，是对流非周期模式的简化，同时也是混沌理论的原型个例[10]。由于Lorenz方程具有较强的非线性，且模型较为简洁，所以常采用orenz-63模型来检验数据同化算法的性能[19–20]。

Lorenz方程为

式中， σ >0，b>0； 参数 σ 、r、b、t分别 表示Prantl数、Rayleigh数、对流尺度联系的参数和时间；x是对流强度；y是 最大温度差；z是对流引起的层变化[21]。模型标准参数一般为σ =10,r=28,b=8/3，从而产生混沌解[22]。

本文采用Lorenz-63模型进行数值试验。首先，对标准参数模型采用四阶荣格库塔（Runge-Kutta）方法积分生成真实场（积分步长设置为 dt=0.01）；随后在一个同化时间窗口内以一定的采样间隔进行观测采集，并在观测数据上加入方差为1的白噪声，生成带噪声的观测数据。具体优化步骤为：根据式（15）计算每次优化迭代之后的参数最优扰动方向；确定最优扰动步长，将计算出的最优扰动叠加到当前参数值上得到下一次优化迭代的参数初值；经过多次迭代，得到收敛的模型参数值，作为最终参数优化结果。本文设置单参数、双参数和三参数试验来检测新方法的模型参数优化能力，并与传统4DVar方法进行模型参数优化对比试验；此外，通过设置不同的模型参数真值、集合成员个数、同化时间窗口长度及观测采样间隔 等敏感性试验，考察新方法的参数估计能力。

3.1 新方法参数优化结果

本节试验积分窗口取500步，集合成员个数取500个，将 σ =10,r=28,b=8/3这些特殊参数值作为本次试验的标准参数值，取背景场状态变量为x0=1,y0=2,z0=3对模式进行积分构造真实场，以10步为采样间隔采集观测并加入白噪声构造观测场。假设初猜的参数值为σ1=9,r1=25,b1=5，并采用相同的背景场状态变量向前积分500步。传统4DVar方法采用了同样的参数设置，编辑伴随模式计算代价函数梯度并采用同样的线性搜索方法优化迭代计算。表1为本试验的主要参数配置。

表1 A-4DEnVar和传统4DVar对Lorenz-63模型的参数优化试验设计Table 1 Experimental design of Lorenz-63 model parameter optimization by A-4DEnVar and traditional 4DVar

本节设计7种试验方案，包括单参数试验、双参数试验以及三参数试验用以检验新方法的模型参数优化能力。结果表明，针对不同个数的参数，新方法均能收敛到真值，对三参数优化后的模型分析场与真实场如图1所示（其余结果未列出）。由图1可知，A-4DEnVar参数优化方法和传统的4DVar参数优化方法均可达到一个理想的优化效果，分析场拟合真实场程度高。各试验中代价函数随迭代变化情况如图2所示。由图2可知，A-4DEnVar在优化迭代过程中代价函数值在100步左右可以实现收敛，收敛结果较为稳定，因而具有良好的模型参数优化能力。

图1 三参数同时优化试验结果Fig.1 Results of three parameters optimization experiment

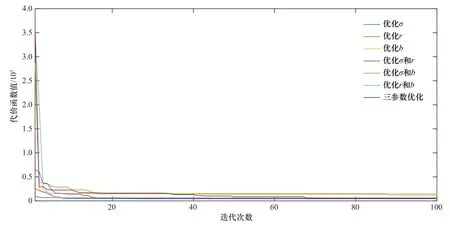
图2 A-4DEnVar代价函数值随迭代次数的变化Fig.2 Changes of value of cost function of A-4DEnVar with the number of iterations

3.2 同化时间窗口长度和观测采样间隔影响

为了测试同化时间窗口长度和观测采样间隔对新方法在模型参数优化方面能力的影响，本节采用与3.1节相同的初始场和初猜参数，选取4组不同的同化时间窗口长度进行试验，并计算分析场与真实场的均方根误差（RMSE）。同化时间窗口长度为：100步、200步、300步和400步，在这4个时间窗口下再分别取5步、10步和20步的观测采样间隔（Observation Sampling Interval，OSI）。为方便对比对比，传统 4DVar方法采用了同样的参数设置进行试验。

图3给出了改变积分时间窗口长度和观测采样间隔后的模型变量的平均RMSE变化。试验结果表明，针对不同的同化窗口和采样间隔，A-4DEnVar方法均可实现模型参数的理想优化，效果与传统4DVar方法相当；新方法的模型参数优化速度较传统的4DVar方法快，这是由于A-4DEnVar方法采用了解析解而不是梯度下降方向作为搜索方向。图4描绘了不同的同化时间窗口和观测采样间隔下优化迭代收敛后的RMSE。结果表明，采用新方法与传统4DVar方法均能使分析场RMSE低于观测误差标准差，可实现模型参数的收敛，同一种方法在同一采样间隔的情况下，随着积分窗口长度的增长，最终收敛的平均RMSE会增大；同一种方法在同一积分窗口长度的情况下，随着采样间隔的增大，最终收敛的平均RMSE会增大。

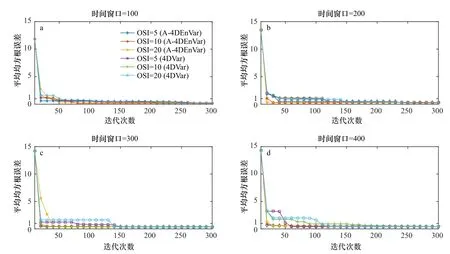
图3 改变积分时间窗口长度和观测采样间隔之后的模型均方根误差变化Fig.3 Model RMSE changes after changing integral time window length and observation sampling interval

图4 不同积分时间窗口长度和观测采样间隔组合下收敛后的平均均方根误差Fig.4 Convergent average RMSE under the combination of different integral time window length and observation sampling interval

3.3 集合成员数量影响

为了测试集合成员数量的大小对新方法参数优化能力的影响，本节采用与3.1节相同的初始场和初猜参数及同化时间窗口和参数标准值，选取4组不同的集合成员数量进行试验。4组集合成员数量分别是：10、100、200和300。试验参数如表3所示。

表2 改变积分窗口长度和观测采样间隔条件下Lorenz-63模型参数优化试验Table 2 Lorenz-63 model parameter optimization experiment under the changes of integral window length and observation sampling interval

表3 不同集合成员数量情况下解析4DEnVar对Lorenz-63模型的参数优化Table 3 Lorenz-63 parameter optimization experiment by A-4DEnVar under different number of members of the set

图5展示了不同集合成员数量情况下模型分析场与真实场的拟合程度。由图5可知，在不同的集合成员数量下，新方法均可实现参数的理想收敛，模型分析场拟合真实场程度高，这说明新方法对集合成员数量不敏感；本节最小集合成员个数取的是10，若再取更小的集合成员个数（例如3或4），则需要更多的迭代次数来实现模型参数的收敛。

图5 改变集合成员数量后模型分析场拟合真实场轨迹Fig.5 Trajectory chart of analysis field fitting real field after changing the number of members of the set

3.4 参数标准值影响

为了测试不同参数标准值对提出方法的影响，本节采用与3.1节相同的初始场和初猜参数及同化时间窗口和集合成员个数，在模式原标准参数上加上一定的扰动倍数，形成3组不同的参数标准值进行组合试验[10]。3种参数所属区间分别是： σ ∈(0.9×10,1.1×10)，r∈(0.9×28,1.1×28)和b∈(0.9×8/3,1.1×8/3)，每个区间生成10个任意值，一共1 000组试验。试验参数如表4所示。

表4 不同参数标准值情况下解析4DEnVar对Lorenz-63模型的参数优化Table 4 Lorenz-63 parameter optimization experiment by A-En4DVar under different standard values of parameters

图6展示了改变模型参数标准值后的各组代价函数值随着迭代次数的变化，横坐标表示组别，纵坐标表示代价函数值。图7展示了改变模型参数标准值后平均代价函数值随着迭代次数的变化，横坐标表示迭代次数，纵坐标表示代价函数值。由图6和图7可知，对选取的1 000组参数标准值，在迭代50步之内，代价函数值即可收敛至最小值，此时模型参数收敛至标准值，由此可知新方法优化能力较强，且对参数的选取不敏感。

图6 改变模型参数标准值后各组代价函数值变化Fig.6 Changes of each group's cost functions after changing the standard values of model parameters

图7 改变模型参数标准值后平均代价函数值变化Fig.7 Changes of average cost function value after changing the standard values of model parameters

4 结论

本文将模型参数视为一种特殊的控制变量，在传统4DVar框架下，以迭代得到的模式参数为基准展开集合扰动，计算误差协方差矩阵。在此基础上，使用代价函数最小值的解析解构造线性搜索最优化方法，提出了A-4DEnVar参数优化方法，避免了传统4DVar方法中的伴随模式的使用。为验证有效性，采用传统的4DVar方法和新的A-4DEnVar参数优化方法对Lorenz-63模型进行参数优化对比试验，针对不同个数的参数，新方法同化效果与传统方法4DVar相当。针对不同的同化时间窗口、观测采样间隔、集合样本个数及不同标准参数的敏感性试验结果显示，新方法能达到一个准确的收敛效果，在较长的同化时间窗口和观测采样间隔时也可以实现理想的模型参数优化效果，并且该方法对集合样本个数和标准参数不敏感，采用较少的集合样本即可达到同化效果，节约了工作量，这在实际模型的参数优化工作中，将具有重要意义。