深水随机波列中畸形波统计特征的研究

付睿丽，马玉祥*，董国海

(1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116023)

1 引言

畸形波，也称突发巨浪、疯狗浪，是指波高不小于 2 倍有效波高（H≥ 2Hs）的波浪[1]。这类波浪因其波高巨大且发生突然，可对海洋结构物和人类生命安全造成严重的威胁[2–6]。畸形波的统计特征和产生机理研究一直是海洋工程领域研究的热点问题。通过大量数据的统计分析是了解畸形波特征的关键，然而由于畸形波的突发性，现场观测得到的数据非常稀少，这对揭示畸形波的特征带来了巨大的挑战。物理模型试验是研究畸形波的重要途径，然而获取大量数据需要开展大量的物理模型试验，导致成本极其高昂，并且受到水池尺寸的限制，数据不可避免受到水深和边壁反射的影响。

以往大量研究表明，Longuet-Higgins随机波浪模型[7]可以很好地描述波浪的统计特征，广泛应用于海洋工程等领域的波浪要素统计、波浪荷载计算和结构安全设计等方面[8]。因此应用Longuet-Higgins随机波浪模型产生大量的数值仿真波浪是开展波浪统计特征研究的有效方法。Gemmrich和Garrett[9]通过Longuet-Higgins随机波浪模型，利用WAFO工具箱[10]，分析了不同谱宽波况中畸形波的重现期，发现畸形波的重现期仅与谱宽有关。与其他产生随机波浪时间序列的方法相比，该工具箱可快速生成足够长时间的随机波浪时间序列，且波面无重复。随后，Gemmrich和Garrett[11]分析了有限水深中畸形波的重现期，发现随着水深变浅，该波的发生频率显著增加。Ghane等[12]利用该模型推导了大于不同波高阈值的波浪持续时间和振幅的联合分布。潘玉萍等[13]利用Longuet-Higgins模型计算了波高−周期联合概率密度分布，并与美国浮标站实测的典型双峰海浪谱进行对比，发现计算的波高与周期联合分布与实测情况基本相同。基于Longuet-Higgins随机波浪模型，毛青等[14]进行了大量随机波的模拟，发现随机波列中出现的畸形波的波高、周期分布符合广义极值分布（GEV分布），畸形波出现的时间间隔符合指数分布。在极端环境下，比如风暴过程，海况的参数是变化的，一般假定一个固定时间内，如3 h，海浪的参数不变[15]。在这段时间内，畸形波的出现频率及间隔时间的分布尚不清楚。很多研究表明，畸形波并不是突然出现的，而大部分是从能量集中的波群中演化出来的[16–18]。因此，研究畸形波所在波群的形态特征和能量分布是深入了解畸形波的必要途径。Osborne等[19]研究表明在巨大波峰前后都会形成深谷；Clauss[20]发现畸形波往往以波群形式出现，在巨浪出现前后也会出现连续的大波。崔成等[21]分析了畸形波群的内部能量，发现在畸形波生成前、后出现的过渡大波中也包含大量高频能量,内部结构和畸形波类似。很多原场观测资料表明[22–24]，一个波群中会有连续的两个甚至3个畸形波产生。然而到目前为止，对随机波列中出现畸形波波群的形态特征的分析仍然不明确，这制约着对畸形波群的生成机理、演化过程及内部结构等方面的研究。

本文采用Longuet-Higgins理论随机波浪模型，基于JONSWAP谱生成大量的随机波面序列，并分析了一定时间内畸形波的发生频率和时间间隔的分布特征，及谱宽对其分布的影响。随后基于小波能量谱分析波群的方法[24]，将随机时间序列分解成独立波群的组合，进而分析了畸形波群中包含不同畸形波个数的比 例和畸形波群时间跨度的分布特征等。

2 波浪模型

2.1 理论随机波浪模型

Longuet-Higgins理论随机波浪模型假设波面由很多单色波叠加而成，在二维波况下，波面表示为[7]

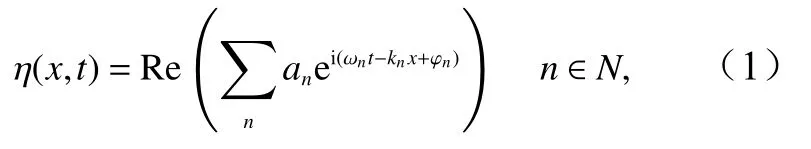
式中，an、ωn、kn、φn分别为第n个波浪元素的振幅、频率、波数和初始相位；N为总波浪元素个数。每个波浪元素的频率和波数满足色散关系

式中，h为水深；g为重力加速度。

2.2 波浪参数选择

本文利用WAFO工具箱[10]，选择JONSWAP谱[25]生成随机波面序列，谱峰升高因子γ从1到7变化，深水随机波浪选择南海1年一遇的波浪参数，即有效波高选择Hs=6 m、谱峰周期为Tp=11 s[26]。每组时间序列包含150万个波浪，时间间隔为dt=0.1 s，在该波浪个数下，畸形波的发生概率已趋于稳定，每组波况包含20个样本。不同谱宽随机时间序列中，包含150万个波浪个数的时间序列长度T0见表1。

表1 不同谱宽的时间序列长度[27]Table 1 Time series lengths for different spectrum widths

在本文中，畸形波的定义为波高不小于2倍有效波高（H≥2Hs）的波浪[1]，其中波高通过下跨零点法计算。

谱宽参数[28]为

式中，m为谱的矩；谱的r阶矩为

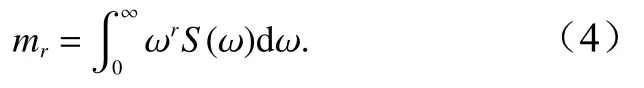
研究表明，不同谱宽的畸形波的发生概率小于基于Rayleigh的分布预测结果（0.033 3%）。与实测海况畸形波发生概率相比，当谱峰升高因子γ=1～3时，对应的畸形波发生概率与台湾岛的概率接近[29]，而当γ=7时，对应的畸形波发生概率与江苏海岸的概率接近[30]，这些波况的畸形波发生概率均小于北海、印度洋、大西洋等的畸形波发生概率[28,31]。

3 畸形波统计特征分析

3.1 畸形波的发生频次

根据Rayleigh分布的统计结果，畸形波大约在3 000个波浪中出现1次[32]。但目前研究对畸形波发生频次分布的研究仍然较少。在实际海况中，一场风暴固定有效波高不变的时间一般为3 h（T）[15]。因此，分析在3 h内，畸形波发生频次的分布非常重要。分析方法如下：

（1）将总时间为T0s的时间序列等分为n段时间长度为T（10 800 s）的时间序列，即

（2）分析在时间T内畸形波出现频次的分布特征，图1展示了γ=1，3，5，7时，畸形波发生频次的概率密度曲线。经过χ2检验，该曲线符合泊松分布，且泊松分布参数λ与谱宽υ呈线性关系（图2），随着谱宽增加，泊松分布参数线性降低，具体为

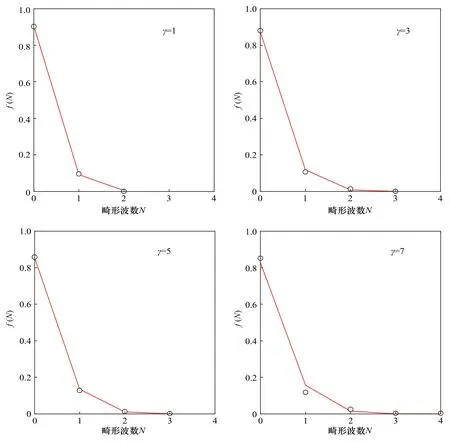
图1 γ=1,3,5,7 时，时间T 内畸形波发生频率的概率密度分布Fig.1 Probability distributions of frequency of freak waves for different peak enhancement factors (γ=1,3,5,7)

图2 泊松分布参数λ与谱宽υ的关系Fig.2 Relationships between Poisson distribution parameterλ and spetrum widthsυ

因此，当γ=1～7时，在Ts内，发生m次的畸形波的概率P(m)为

为验证公式（7）的准确性，选择谱峰因子为γ=2，4，6 的时间序列进行测试。经检验，当γ=2，4，6 时，时间T内畸形波的发生频次同样服从泊松分布。根据式（7）计算发生1次、2次畸形波的概率，并与WAFO工具箱生成的数值时间序列得到的概率值比较，相对误差见表2，其中相对误差为

由表2可见，式（7）计算得到的畸形波发生频次的概率与数值结果误差不超过2.2%，说明式（7）可以较准确地估算出深水条件下在3 h内发生畸形波频次的概率。进一步地，改变时间T，验证泊松分布参数的鲁棒性。分别分析了T=6 h，9 h，12 h 内畸形波的发生频次，发现在不同时间段内畸形波的发生次数均服从泊松分布，且泊松分布系数λ保持不变，说明在理论随机波浪模型中，畸形波发生次数的概率分布较稳定，不随时间范围变化。

表2 不同谱宽下畸形波出现不同频次概率的预测值与数值结果对比Table 2 Comparisons of the numerical and predicted values of possibility for frequencies of freak waves

3.2 相邻畸形波的时间间隔

进一步分析相邻畸形波之间的时间间隔分布，其中畸形波的时间间隔根据畸形波对应的下跨0点的时间差确定。不同谱宽下，相邻畸形波的无量纲时间间隔（以谱峰周期Tp为标准）的概率分布见图3，红色实线表示指数分布拟合的曲线，经过K-S检验，相邻畸形波的时间间隔Td服从指数分布，即

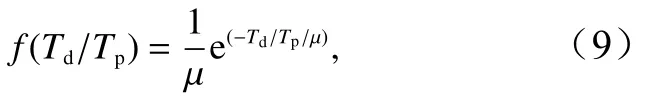
图3 γ=1，3，5，7 时，畸形波出现时间间隔分布Fig.3 Probability distributions of time intervals of freak waves for different peak enhancement factors (γ=1,3,5,7).

式中，Td为相邻畸形波的时间间隔；Tp为谱峰周期；μ为指数分布参数。

不同谱宽的指数分布参数μ与谱宽的关系见图4，随着谱宽υ的增加，指数分布参数μ线性增加，即随着谱宽的增加，相邻畸形波的时间间隔逐渐增大。具体满足

图4 指数分布参数μ 与谱宽υ的关系Fig.4 Relationships between exponential distribution parameterμ and spetrum wdthsυ

因此，相邻畸形波的时间间隔Td的概率分布为

为验证式（11）的准确性，选择γ=2，4，6 的波况进行测试，根据式（11）分别计算相邻畸形波的出现时间间隔分别为Td/Tp=0.5×104，1.5×104的概率，并与数值统计结果进行对比，见表3。预测值与数值结果的误差在5%以内，说明式（11）可以准确地估算出γ=1～7时相邻畸形波的时间间隔。

表3 不同谱宽下相邻畸形波时间间隔预测值与数值结果对比Table 3 Comparisons of the numerical and predicted values of intervals of adjacent freak waves

3.3 畸形波群波形特征及时间跨度

畸形波发生突然且持续时间较短，对于单一畸形波特征的分析具有很大的不确定性，而畸形波往往产生于独立的波群中。因此，通过分析波群，可以更方便准确地分析包含畸形波的波群特征。

在本文中，根据小波能量谱，将时间序列分解成独立的波群[24]。根据波群中包含畸形波的数量，可以分为只有一个畸形波的波群和包含多个畸形波的波群。在本次分析中，发现一个畸形波群最多包含4个畸形波。对于单个畸形波的波群，畸形波同时具有最深波谷和最高波峰的比例最高。但也有些波群，最深波谷和最高波峰在畸形波附近出现。对于包含多个畸形波的波群，畸形波有可能连续出现，也有可能间断出现。具体畸形波群的特征总结见表4。

表4 波群中包含畸形波的类型Table 4 Classifications of freak waves in wave groups

不同谱宽下各类不同特征畸形波群所占的比例如图5所示。可以看出，当γ=1时，只有一个畸形波的波群占99.33%，随着谱峰升高因子增加（谱宽变窄），畸形波群中包含多个畸形波的比例逐渐增加；当γ=7时，只有1个畸形波的波群占88.91%，包含2个畸形波的波群占9.32%，1个畸形波群中最多可以包含4个畸形波，但概率非常小，最大仅为0.54%。对于只有1个畸形波的波群，畸形波同时具有最深波谷和最高波峰的概率最大，占64%以上。

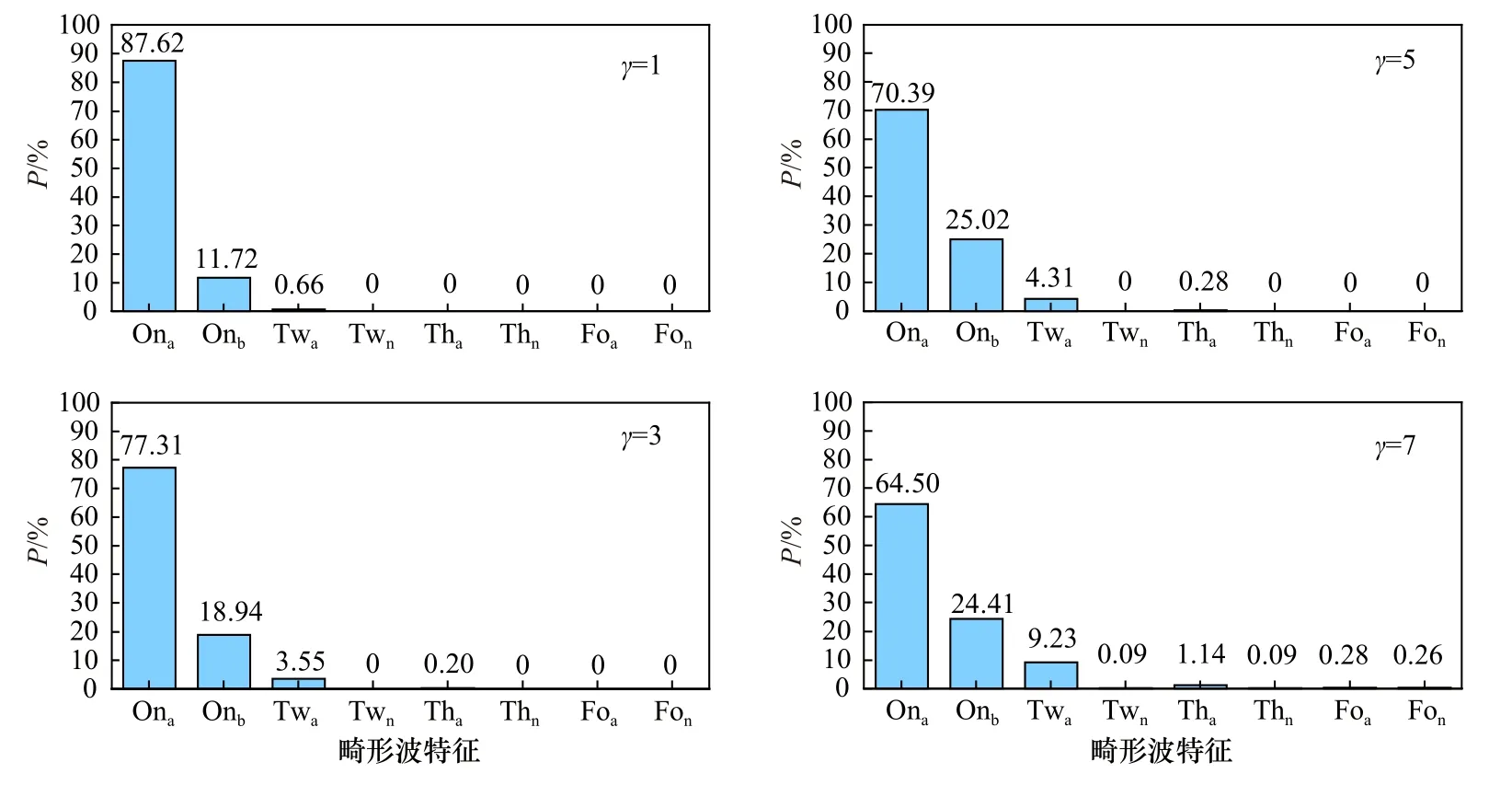
图5 不同谱峰因子下，不同畸形波特征所占比例Fig.5 Proportions of each characteristic of freak waves for different peak enhancement factors

随后，分析畸形波群的时间长度分布，不同谱峰因子下，畸形波群的无量纲时间长度概率分布见图6。随着谱宽变窄，畸形波群的时间长度范围逐渐增加。当γ=1时，畸形波群最有可能出现的无量纲时间长度为7个谱峰周期，而当γ=7时，畸形波群的无量纲时间长度的众数为11个谱峰周期，且不同时间长度的概率分布逐渐均匀。通过K-S检验法，不同谱宽的畸形波无量纲时间长度可以较好的服从GEV分布。

图6 γ=1，3，5，7 时，畸形波群无量纲时间长度概率分布Fig.6 Probability distributions of non-dimensional time lengths of freak wave groups for different peak enhancement factors (γ=1,3,5,7)

在 GEV 分布中，包含 3 个参数：a,b,c。因此，畸形波群无量纲时间长度可表示为

不同谱宽下，系数a,b,c的变化见图 7。随谱宽变窄，系数a,b呈指数增加，而c更符合线性增长。具体为

图7 GEV 系数与谱宽υ的关系Fig.7 Relationships between parameters of GEV distribution and spetrum widthsυ

为验证式（12）和式（13）的适用性，选择谱峰因子γ=2，4，6 进行验证。根据式（12）和式（13）计算畸形波群无量纲时间跨度的众数，并与WAFO工具箱生成波面的数值结果比较，见表5。可以看出，式（12）和式（13）计算的畸形波群无量纲时间跨度与数值结果几乎完全一致，说明式（12）和式（13）能够较准确地计算出不同谱宽下畸形波群无量纲时间长度分布。

表5 畸形波群无量纲时间长度众数预测值与数值结果对比Table 5 Comparisons of the numerical and predicted modes of the non-dimensional lengths of freak wave groups

4 结论

本文基于Longuet-Higgins随机波浪模型，选择南海1年一遇的波浪参数（有效波高选择Hs=6 m、谱峰周期为Tp=11 s[26]），利用 WAFO 工具箱，模拟了畸形波发生概率稳定的不同谱宽JONSWAP谱的随机波列。研究表明，当畸形波定义为波高不小于2倍有效波高（H≥2Hs）时，随机序列中畸形波的出现次数小于瑞利分布对应的概率值。在固定时间段内，畸形波出现的次数服从泊松分布，而出现时间间隔服从指数分布，且随着谱宽的增加，畸形波在最有可能发生的频次线性减小，而相邻畸形波出现的时间间隔相应增加。

此外，基于小波变换方法分离出随机波中的波群[24]，进而研究了出现畸形波的波群特征。发现在一个波群中，最多可出现4个畸形波，存在单个畸形波且该波同时具有最深波谷和最大波峰的可能性最大，约占64%以上；一个波群中出现2个畸形波的概率最大为9.32%，3个畸形波的概率最大为1.23%，4个畸形波的概率最大为0.54%。随着谱宽变窄，一个波群中包含多个畸形波的概率增加，而出现单个畸形波的概率相应减小。出现畸形波的波群时间长度服从GEV分布，且随着谱宽变窄，出现的畸形波群的时间跨度逐渐增加。