基于聚类及优化集成神经网络的地铁车站空调负荷预测

孟 华，孙 浩，裴 迪，王 海，李元阳，徐 敏

（1.同济大学机械与能源工程学院，上海 201804；2.广东美的暖通设备有限公司美的全球创新中心，广东佛山 528311；3.上海克来沃美的暖通设备有限公司，上海 200335）

2019年我国轨道交通总耗电量约152.6亿千瓦时，占全国年总耗电量的2.4‰［1］；我国南方地区地铁车站空调环控能耗约占总能耗的50%以上［2］。地铁车站空调系统能耗大的主要原因是系统运行调控供需不平衡，而要想缓解不平衡、实现节能运行，首先必须对地铁车站空调负荷进行准确预测。学者们已在地上建筑空调负荷预测方面做过大量研究，既有传统的参数回归法（简单回归模型、多变量回归模型、高斯过程回归［3］等）；时间序列法（自回归模型、线性与非线性方程模型［4-5］）、滑动平移模型［6］、混沌法［7］、小波分析法等［8］；也有基于黑箱的误差反向传播 神 经 网 络［9-10］（back-propagation neural network，BPNN）及基于数据聚类［11-12］和优化算法［13-16］的负荷预测。

但是，目前针对地铁车站空调负荷预测的研究还较少。地铁车站属于地下建筑，仅通过出入口通道及地面风亭与外界相连，站内客流、设备、屏蔽门、列车运行产热、活塞风及周围土壤传热等因素，都使得地铁车站空调负荷特点不同于地上建筑，其系统控制变量多、高度非线性、惯性大滞后强，若采用传统空调负荷预测方法难度较大，而日益完善的地铁车站空调自控系统使得基于大数据的黑箱负荷预测模型成为有效方法。文献［17］采用BPNN模型预测地铁站厅空调负荷，但其数据集是采用仿真模拟结果。文献［18-19］利用遗传算法优化BPNN模型以预测地铁车站冰蓄冷空调负荷，但模型输入参数是定性选取的。文献［20］利用基因遗传及粒子群算法优化BPNN模型以预测地铁车站空调负荷，但文中数据集情况不详。

目前在地铁车站空调负荷预测研究中，关于定量表征各因素对负荷影响程度随时间的动态变化特征以及采用不同优化算法模型对负荷预测精度及预测效果进行比较等研究目前还很有限。本文分别从优化算法集成神经网络（PSO-BPNN与FOABPNN）及将数据聚类（Kmeans-BPNN）后按类分别建模两方面建立地铁车站空调负荷预测模型。根据实际运行数据，定量分析各物理量对负荷影响程度随时间变化的动态特征，获取相关系数曲线，并以此甄选模型输入参数。基于所提出的3种模型对地铁车站空调负荷进行逐时预测，利用4种指标对预测结果进行评价，从优化算法集成建模及从对数据集进行前处理后再建模2个维度，总结精度更高和效果更好的地铁车站空调负荷预测方法。

1 预测模型

1.1 Kmeans聚类-BPNN模型

单纯BPNN［21］模型直接利用数据集进行训练及预测，不考虑数据集的特征。作为无监督学习的一种算法，聚类将数据集中所有待预测样本划分为若干个互不相交的子集，即“簇”［22］。K均值（Kmeans）聚类通过针对样本集D=｛x1，x2，…，xm｝划分所得簇C=｛C1，C2，…，Ck｝，使其平方误差E最小，即

式中：x为单个样本；Ck为单个簇；μk为簇Ck的均值向量，其公式为

利用Kmeans聚类后再根据各类分别构建BPNN模型。

1.2 粒子群优化算法集成BPNN模型（PSO-BPNN）

粒子群优化算法（Particle Swarm Optimization，PSO）［23］将觅食的鸟类作为N维空间搜索个体，其速度与位置的更新方法为

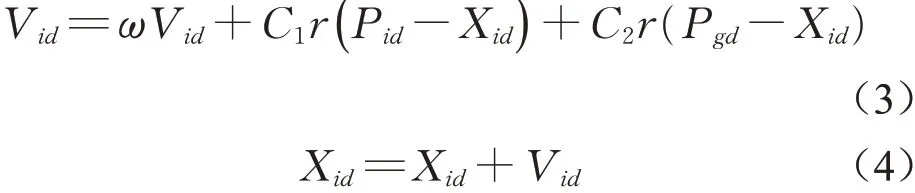
式中：ω为惯性因子；C1和C2分别为每个粒子的个体与社会学习因子；r为在区间［0，1］上的随机数；Xid和V id分别为d时刻第i个粒子的位置和速度；V id为d时刻第i个粒子的个体最优解；Pgd为d时刻所有粒子g的全局最优解。

模型集成原理为：每次PSO算法将迭代得出的全局最优解粒子速度与位置赋值给BPNN模型的权值及阈值，将模型训练得出的预测值与实际目标误差作为适应度函数，直至满足适应度函数，则PSO优化算法迭代停止，其粒子的速度与位置即为BPNN的最优权值与阈值。

1.3 果蝇优化算法集成BPNN模型（FOA-BPNN）

果蝇优化算法（Fruit Fly Optimization Algorithm，FOA）［24］是以模拟果蝇觅食寻求全局优化的算法。果蝇的位置更新表达式与味道浓度判定函数为

式中：Xaxis为果蝇在轴线X初始位置；rrandomValue为果蝇活动范围内的随机值；Si表示果蝇i闻到食物的味道浓度值；SSmell为判定函数。

模型集成原理为采用FOA算法不断优化BPNN模型的拓扑结构，将迭代寻优的果蝇最佳位置赋给BPNN权值与阈值，以提高模型的预测性能及泛化能力。

本文提出的Kmeans-BPNN、PSO-BPNN、FOA-BPNN预测模型流程如图1。

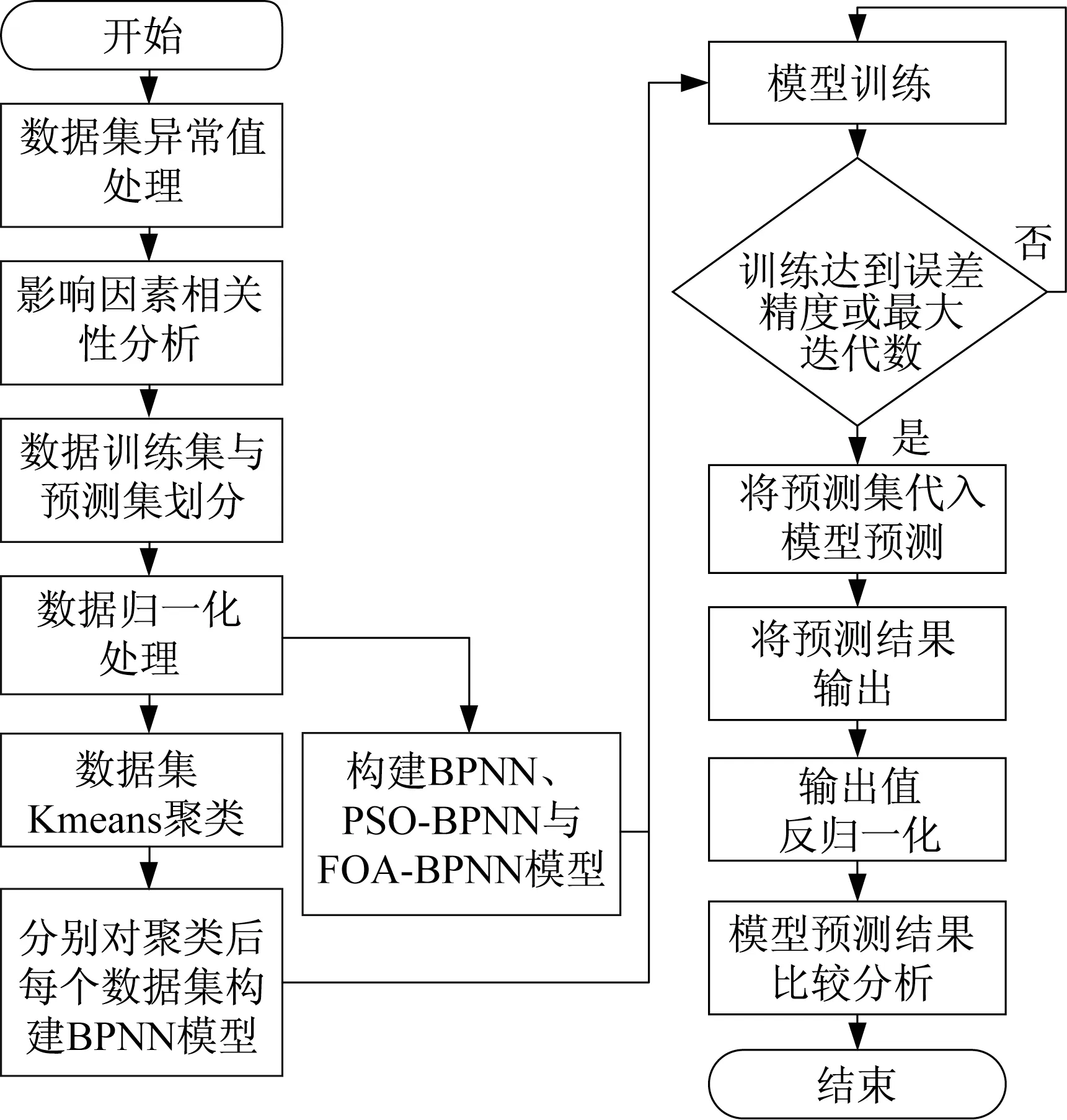
图1 预测模型流程Fig.1 Flowchart of prediction models

1.4 预测模型的评价指标

采用4项指标对各预测模型进行评价：相关系数R、平均绝对误差（mean absolute error，EMAE）、均方根误差（root mean square error，ERMSE）与平均绝对百分比误差（mean absolute percentage error，EMAPE），计算公式为（7）-（10）。

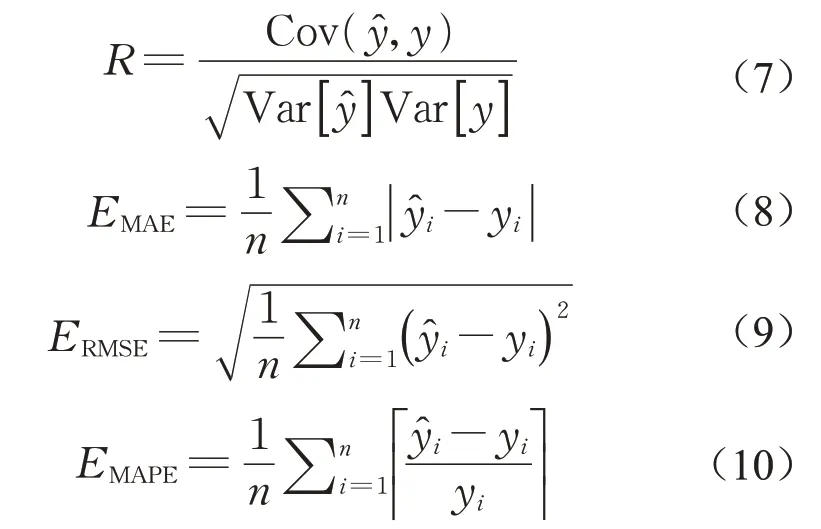
式中：Cov（）为预测值与实际值y的协方差；Var［］、Var［y］分别为预测值与实际值y的方差；n表示预测时长；及yi分别为第i时刻的预测值和实际值。

2 地铁车站空调负荷预测实例分析

2.1 数据来源及处理

以广州某地铁车站空调系统实际运行数据作为样本集，该站共设2台冷水机组。原始数据包括2台冷机的冷水供、回水温度，冷却水供回、水温度，2台冷机的瞬时冷量，站台层A、B端及站厅层A、B端各4个采集点的空气温度及相对湿度，以及地铁站台入口处的室外空气温度和相对湿度；采集时间段为2020年5月1日0时至8月31日23时，数据采集间隔2min，共计88 560组数据。对样本集进行了训练集及测试集的划分。

数据采集期间广州地铁车站夜间也有冷机运行。通过对原始样本的分析发现，空调负荷存在在白天地铁正常运营时很小甚至为零而夜间机组部分关闭时却很大等不合理现象，这可能是由于2台冷机切换运行或数据传输系统瞬时不稳定所致。为避免模型训练难以收敛、预测误差较大等后果，需对原始数据异常值进行处理。本文利用平均值或样条插值对负荷值为零、过大、过小或缺失等处进行替换或补充。原始数据集处理后的空调负荷如图2。后面所有预测模型都以处理后的负荷值作为原始样本。其他采集参数无异常。

图2 空调负荷异常值的处理Fig.2 Treatment of abnormal data of cooling load

2.2 预测模型输入参数的确定

本文采用黑箱方法建立地铁车站空调负荷的预测模型，包括BPNN模型在内的所有黑箱模型都是通过对历史数据自学习来映射出待预测物理量与对该量产生影响的其他各物理量之间的关系，而这些物理量对负荷的影响程度具有随时间变化的动态特征，定量分析这些动态特征将对准确选择模型输入参数及确保模型预测精度至关重要。由于地铁车站位于地下，土壤具有很大的蓄热性及传热惰性，因此太阳辐射及风速等参数对地铁车站空调负荷影响很小。根据文献［17-18，20］调研，初选地铁车站室内、外空气温度、相对湿度及历史负荷作为影响因素。考虑这些物理量在不同历史时刻对负荷的影响程度不同，现采用SPSSStatistics 21软件对上述5个量在过去24h（记为t～t-24）内对地铁车站空调负荷的动态影响程度进行定量分析，利用Person相关系数r作为衡量影响负荷程度强弱的指标。

式中：N为特征样本数量；xi和yi分别表示第i个影响因素与历史负荷。通过定量计算，各物理量在过去24h内对地铁车站空调负荷相关系数的动态变化如图3。

图3 不同物理量对负荷影响相关系数的动态变化Fig.3 Dynamic variation of correlation coefficient of different parameters on load

由此可见前述5个物理量在过去24h内对地铁车站空调负荷的影响程度随时间呈现某种动态变化特征。首先根据定性分析，空调负荷与室内外温度呈正相关，而图3中室外温度与历史负荷在t-9到t-17时刻为负值，违反定性分析，故需要剔除此时间段室外温度。随后根据定量分析，室外温度线上的t时刻和室内温度线上的t-18时刻所对应的r值最高，说明这2个参数在这2个时刻比其他时刻对负荷的影响程度更大。同理根据定性分析，空调负荷与室内外相对湿度呈负相关，图3中室外相对湿度与历史负荷在t-4到t-20时刻为正值，室内相对湿度与历史负荷在t到t-24时刻均为正值，违反定性分析，故需要剔除这2个时间段室内外相对湿度。定量分析可得室外相对湿度在t-24时刻比其他时刻对负荷的影响更大。而历史负荷在t-1、t-2及t-24时刻比其他时刻对当前负荷的影响更大。通过各物理量对负荷相关系数的动态变化分析，最终确定地铁车站空调负荷的6个重要影响参数，并将其作为预测模型的输入参数。根据Kolmogorov定理，经仿真试验确定隐含层节点数为13，预测模型的结构为6-13-1，模型参数见表1。

表1 预测模型的结构参数Tab.1 Construction parameters of prediction mod⁃els

确定数据集后，还需要对数据进行归一化处理，最终模型输出参数经反归一化处理即可得到负荷预测值。

通过分析发现原始样本中空调负荷呈现一定特点，因此本文利用Kmeans聚类对数据集进行预处理，并针对聚类后的各类数据分别建立BPNN模型；此外，还利用PSO与FOA优化算法集成BPNN模型。将这些模型结果与单纯BPNN模型加以比较，以考察其对地铁车站空调负荷预测精度的影响。

经仿真试验确定各模型中的超参数见表2。

表2 模型训练中的超参数Tab.2 Hyper parameters for each model

2.3 聚类神经网络预测模型结果及分析

2.3.1 Kmeans聚类结果及分析

本文利用Python中sklearn库调用Kmeans聚类算法，每个类别之间的距离选择Euclidean（欧氏）距离。利用Calinski Harabasz（CH）评价指标确定最佳聚类数，CH越大代表类之间样本距离越小，联系越紧密，聚类效果越好。部分聚类数及对应的CH评价指标计算结果见表3。而当聚类数大于7后，CH值显著下降，聚类效果较差。根据表4的结果把数据集聚为2类，聚类结果如表4。

表3 不同聚类数的CH值Tab.3 CH for different clustering numbers

表4 Kmeans聚类结果Tab.4 Clustering results of Kmeans

由表4可见，通过Kmeans聚类后的数据被分为A、B 2类，A类数据主要集中在5、7月几天及8月整月，这些天气负荷相对低些；而B类数据集中在6、7月，这段时期负荷相对较高。

2.3.2 Kmeans-BPNN预测结果及分析

利用聚类后的A、B 2类数据分别建立BPNN模型进行地铁车站的空调负荷预测，同时对未聚类数据也建立BPNN模型。2种模型的训练集及预测集相同，测试集8月31日的数据聚类于A类。2种模型的负荷预测值见图4，它们对实际负荷的相对误差见图5。

图4 Kmeans-BPNN及BPNN模型的负荷预测Fig.4 Comparison od load prediction for Kmeans-BPNN model and BPNN model

图5 Kmeans-BPNN及BPNN模型负荷预测的相对误差Fig.5 Relative errors of cooling load prediction for Kmeans-BPNN model and BPNN model

由图5可见，无论是Kmeans-BPNN模型还是BPNN模型的负荷预测值都与实际值相差不大，预测相对误差基本在15%以内，经计算其相关系数R最低为0.912，说明采用本文前述的以各物理量对负荷相关系数的动态变化特征定量甄选模型输入参数的方法能够产生较好的预测效果。同时由图4可见，通过聚类后的Kmeans-BPNN模型比单纯BPNN能够更好地追踪实际负荷的变化特点，尤其在中午11：00-13：00期间，当地铁车站空调负荷逐渐降低时，Kmeans-BPNN的预测值在经过一小段时滞后也能显示出相似的变化趋势；尽管8月31日是周一工作日，但实际负荷在17：00时后变化平稳直至夜里23：00时后降低，Kmeans-BPNN模型的预测值也基本能反应实际特点。从图5也可见Kmeans-BPNN模型预测的相对误差最大值在5%之内，较单纯BPNN总体误差更低，预测精度更高。这说明在地铁车站空调系统实际运行中，若历史负荷变化呈现一些特点，则采用数据聚类神经网络模型比单纯BPNN模型具有更高的预测精度。

2.4 优化算法集成神经网络预测模型结果及分析

从优化算法集成神经网络的角度分别建立PSO-BPNN与FOA-BPNN模型。与传统BPNN训练过程不同，优化算法集成模型先根据所设定的训练超参数对初始种群进行迭代寻优，用每次寻优结果更新BPNN中的权值和阈值，直至满足适应度函数，最终用最优种群迭代结果确定神经网络的结构参数。PSO-BPNN、FOA-BPNN及BPNN模型对地铁车站空调负荷预测值的对比如图6。它们对实际负荷的相对误差见图7。

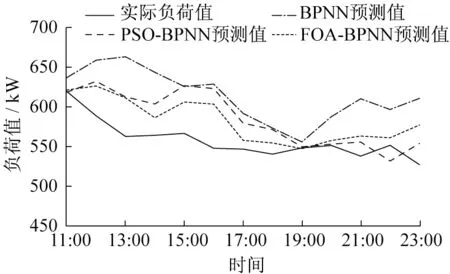
图6 PSO-BPNN、FOA-BPNN及BPNN模型的负荷预测Fig.6 Comparison of load prediction for PSOBPNN,FOA-BPNN,and BPNN model

图7 PSO-BPNN、FOA-BPNN及BPNN模型预测的相对误差Fig.7 Relative errors of cooling load prediction for PSO-BPNN,FOA-BPNN,and BPNN model

由图可见，采用3种模型预测地铁车站空调负荷的最大相对误差低于17%，采用2种算法集成模型的预测值较单纯BPNN精度更好，更能反应实际负荷的变化特点，例如当负荷在中午11：00时到16：00时呈现先逐渐降低、后变化平稳然后再降低时，2种优化集成模型都能基本表现出类似的变化趋势。这主要由于无论是PSO算法还是FOA算法都具有较好的全局搜索力，而BPNN模型具有快速局部搜索力，二者结合可避免后者易陷入局部极小等缺陷，有利于提升模型预测精度。

2种优化集成模型相比，FOA-BPNN在大部分时间似乎比PSO-BPNN预测表现更佳，只是在晚上19：00时之后预测性能略差。由图7也可看出，2种优化集成模型的预测相对误差都比BPNN降低，预测精度更高；而FOA-BPNN总体比PSO-BPNN模型的预测误差更低，精度更高。

2.5 各类模型的预测结果比较及分析

为了更准确地评价各类模型的预测性能，选取4项指标对其进行评价比较，见表5、表6。由表可见，4种模型预测的最小相关系数为0.912，最大相对误差为7.46%，这说明本文利用不同物理量对负荷相关系数随时间的动态变化特征来定量选择模型输入参数的方法效果较好。

表5 各类模型负荷预测评价指标Tab.5 Evaluation indicators of load prediction for each model

表6 各类负荷预测模型评价指标对比Tab.6 Comparison of evaluation indicators of different load prediction models

利用优化算法集成BPNN模型比单纯利用BPNN模型可使预测误差有不同程度的降低，PSOBPNN预测负荷均方根误差为37.838kW，比单纯BPNN的43.164kW降低12.34%，预测平均相对误差较BPNN的7.46%降低到5.53%，降低了25.87%；而FOA-BPNN预测负荷均方根误差为30.981kW，比单纯BPNN降低28.22%，预测平均相对误差为4.47%，较BPNN降低了40.08%，

这说明采用2种优化集成模型都比单纯采用BPNN模型的预测精度有提高。2种集成模型相比，利用FOA算法优化BPNN的性能表现更好，预测平均相对误差较低。

利用数据聚类预处理的Kmeans-BPNN预测负荷的均方根误差仅为14.769kW，平均相对误差仅为2.15%，不仅显著低于BPNN模型，也比优化算法集成的PSO-BPNN及FOA-BPNN预测平均相对误差分别低61.12%和51.90%。

由此可见，在相同的样本集下，通过对模型输入参数的定量分析，在考察实际负荷变化特点的基础上，采用对数据集进行聚类后BPNN模型的预测效果比采用优化算法不断优化更新BPNN模型结构的预测精度更好，效果更佳。

3 结论

为更准确地预测地铁车站空调负荷以降低系统运行能耗，建立了PSO-BPNN和FOA-BPNN 2种优化算法集成神经网络模型及Kmeans聚类神经网络模型，利用广州某地铁车站空调系统实际运行数据对模型进行训练和预测，并将结果与单纯BPNN模型进行比较分析，主要结论如下：

（1）通过定量分析发现，同一物理量对负荷所产生的影响程度随时间呈现某种动态变化特征。比如前1h、前2h以及前一天当前时刻的历史负荷就比其他时刻对当前负荷的影响程度更大；而前一天当前时刻的室外相对湿度也比前1小时或前几小时对负荷的影响程度更大。因此若能根据历史数据定量分析主要物理量对负荷影响程度随时间的动态变化特征，则对精准筛选模型输入参数、提高模型预测精度大有裨益。

（2）采用2种优化算法集成BPNN模型进行负荷预测，PSO-BPNN和FOA-BPNN模型的预测平均相对误差较单纯BPNN分别降低25.87%和40.08%；而2种优化集成模型相比，FOA-BPNN的模型预测平均相对误差较低，性能表现更好。这说明在地铁车站空调负荷预测时，在同等情况下（比如模型输入参数、训练集和测试集等相同）如果利用优化算法集成BPNN往往能够获得精度更高的预测效果，至于具体采用何种优化算法集成模型效果更好则需要通过仿真试验决定。

（3）采用对数据集聚类后按类分别建立BPNN模型进行负荷预测，Kmeans-BPNN模型的预测平均相对误差仅为2.15%，不仅显著低于BPNN模型，也比PSO-BPNN及FOA-BPNN模型的预测平均相对误差分别降低61.12%和51.90%。这说明在同等情况下，在区分实际负荷变化特点基础上，采用对数据集进行聚类后BPNN模型的预测效果可以比采用优化算法不断优化更新BPNN模型结构的预测精度更好，效果更佳。

作者贡献声明：

孟 华：参与研究的构思、设计，对主要学术性内容做文稿修订。

孙 浩：进行研究的构思、设计、数据运算、起草论文。

裴 迪：参与研究的构思、设计。

王 海：对重要学术性内容提出建议、做出修订。

李元阳：参与试验数据的测试及收集。

徐 敏：参与试验数据的测试及收集。