氢正仲转化耦合流动换热板翅式换热器研究

徐攀,文键,厉彦忠,王斯民,屠基元

(1.西安交通大学能源与动力工程学院,710049,西安;2.西安交通大学化学工程与技术学院,710049,西安;3.皇家墨尔本理工大学工学院, VIC 3083, 澳大利亚墨尔本)

氢能具有来源广泛、利用形式多样、环境友好的优点,被普遍认为是无碳化能源系统中理想的能源载体[1-2]。考虑氢能的储运特点和利用形式,液氢是氢能最有前景的利用形式[3-5]。现运行的氢液化工厂均存在能耗高和产量低的问题[6-8],许多研究者为此提出了一系列新型氢液化流程,其产量和能耗指标均得到明显的改善[9-14]。许多新型氢液化流程中均提及了换热器与正仲转化器相结合的新技术[7,15-17],该技术具有增加换热、缩小设备体积和优化系统流程的优点。部分学者基于催化与换热一体化的概念在板翅式甲醇制氢反应器方面进行了相关研究[18-20]。Skaugen等设计了采用正仲转化与流动换热一体化技术的两种Claude氢液化循环,并通过分析法分析了两个循环中各个换热器的损失[15]。Wilhelmsen等建立了一个正仲转化耦合流动换热板翅式换热器模型,发现热梯度和氢正仲转换是板翅式换热器破坏的两个主要来源[21]。Donaubauer等在已有的实验数据[22]的基础上,提出了一阶动力学模型和Langmuir-Hinshelwood模型两种氢正仲转化动力学模型,研究了压力和冷侧流量对板翅式反应器性能的影响[23]。Hånde等研究了运行压力对29.3～47.8 K内正仲转化耦合流动换热板翅式换热器热力学性能的影响[24]。Park等基于实验数据得到了新的压降关联式,并通过数值模拟研究了催化剂填料式板翅式换热器流动换热性能[25]。目前大部分正仲转化与流动换热一体化的研究仅停留在概念分析和流程应用等方面,氢气在催化剂填料的微小通道内的正仲转化与流动换热耦合机理尚不明确。本文在对比分析已有氢正仲转化动力学模型的基础上,研究了42～70 K温度区间内氢气在催化剂填料的平直翅片通道内正仲转化反应与流动换热的耦合过程,为正仲转化与流动换热一体化技术在氢液化流程中的应用提供了理论参考。

1 模型构建

1.1 物理模型

如图1所示,以氢液化流程中两股流板翅式换热器为研究对象,其中冷侧为正常氢气,只有流动换热过程;热侧为主流氢气,催化剂填充到翅片通道内,氢气在流动换热过程中进行正仲转化反应;冷侧和热侧的翅片结构相同:高度h=6.5 mm,间距s=2.1 mm,厚度δt=0.3 mm;隔板厚度δp取1 mm;翅片长度l取2.5 m。

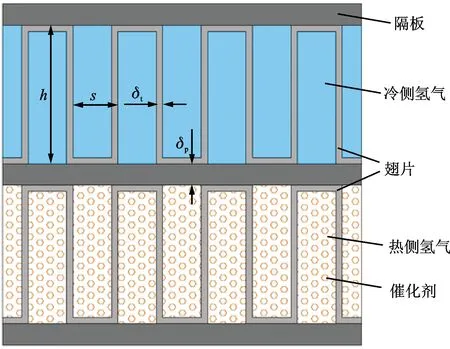
图1 板翅式换热器两层翅片模型

1.2 数学模型

计算模型基于以下假设条件:

(1)冷侧为正常氢气,即由25%仲氢和75%正氢组成(均为体积分数);热侧为主流氢气,入口仲氢体积分数为57.7%,在翅片通道内催化剂的作用下,仲氢组分不断发生变化;

(2)冷热侧工作介质均是由仲氢和正氢组成的单相、不可压缩理想气体;

(3)热侧翅片通道内催化剂填料均匀、颗粒直径与空隙率相等;

(4)采用多孔介质模型简化热侧的流动换热过程;

(5)翅片通道内的冷热侧氢气流动与传热是稳态的。

基于以上假设,冷热侧氢气流动和换热过程均由质量守恒方程、动量守恒方程和能量守恒方程来描述,各方程形式如下。

组分质量守恒方程为

(1)

Sm,i=Miri

(2)

总的质量守恒方程为

(3)

(4)

动量守恒方程为

(5)

(6)

(7)

(8)

能量守恒方程为

·(λeT)+Se

(9)

Se=MrΔH

(10)

以上各式中:ε为孔隙率;ρf为气体密度,kg/m3;Yi为组分i的质量分数;t为时间,s;u为速度,m/s;Dm,i为组分i的气体扩散系数,m2/s;Sm,i为质量源项,kg/(m3·s);Mi为摩尔质量,kg/mol;ri为正仲转化反应速率,mol/(m3·s);p为压力,Pa;τ为应力张量,Pa;g为惯性力加速度,m/s2;S为动量源项,kg/(m2·s2);μ为黏度,Pa·s;α为渗透率,m2;C1为惯性阻力系数,1/m;dp为催化剂颗粒直径,m;Ef为流体含有的能量,J/kg;ρs为催化剂密度,kg/m3;Es为固体含有的能量,J/kg;λe为床层有效导热系数,W/(m·K);T为温度,K;Se为能量源项,W/m3;r为正仲转化反应速率,mol/(m3·s);ΔH为正仲转化反应的反应热,J/kg。

平衡氢中的仲氢体积分数是温度的函数,采用温度相关方程表示[21]为

(11)

Wilhelmsen等基于表面反应控制假设得到的Elovich计算模型[15,21]为

(12)

式中:yH2,p为主流氢中仲氢体积分数;K为Elovich计算模型的反应速率常数,mol/(m3·s)。Donaubauer等基于一阶动力学和Langmuir-Hinshelwood动力学方程得到了两种计算模型[23]。

一阶计算模型

(13)

Langmuir-Hinshelwood计算模型

(14)

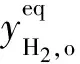
催化层的结构和性能参数如表1所示,催化剂为Fe2O3。计算模型如图2所示,冷热流体逆流布置,选择一个翅片单元进行计算,并采用左右对称和上下周期边界条件进行拓展。参考Skaugen等的氢液化流程[15]中42～70 K温区的填料式换热器,热侧的主流氢气运行压力为2 MPa,冷侧的回流氢气运行压力为0.8 MPa;根据热平衡计算,冷热侧的流体质量流量比为2.03,热侧入口Re=500～1 500对应冷侧入口Re=1 563～4 688;冷热侧的换热温区为42～70 K,对应的氢气物性、正仲转化热和翅片材料物性变化较大,采用实际物性的拟合关联式进行计算。为了消除入口和出口效应的影响,在翅片入口和出口各加了20 mm的延长段。采用Fluent作为求解器,湍流模型选择SSTk-ω模型,采用增强壁面函数处理近壁面处的流动,入口端和出口端壁面设定为绝热壁面。各方程离散格式都采用二阶迎风格式,收敛残差均设为1×10-6。

表1 催化层结构和性能参数

图2 板翅式换热器两层翅片计算模型

1.3 数据处理

对于平直翅片通道,定义水力直径Dh[26-27]为

(15)

结果分析中需要用到的无量纲准则数包括Re、Nu和Pr,分别定义为

(16)

(17)

(18)

式中:αh为流体侧对流换热系数,W/(m2·K)。对于板翅式换热器,常采用Colburn传热因子j和Fanning摩擦因子f来描述其流动换热性能特征,分别定义[26-27]为

(19)

(20)

式中:GA为单位流动面积质量流量,kg/(m2·s)。采用换热增强因子F来评价换热器综合性能

(21)

2 计算模型验证

2.1 网格无关性验证

采用ANSYS Meshing进行网格划分,考虑通道内边界层流动情况,对流固交界面进行网格加密,区域离散化结果如图3所示。如图4所示,当热侧Re=1 000时,网格数为2 833 152的j因子、f因子、换热增强因子和出口仲氢体积分数相对于更大的网格数变化均小于0.5%,因此选择网格数为2 833 152。

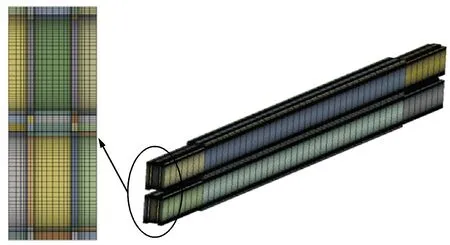
图3 区域离散化结果

(a)j因子和f因子

2.2 翅片通道流动换热

已有的文献中缺乏氢气在翅片内的流动换热的实验数据,因此采用文献[26]和文献[27]的空气在常温下平直翅片通道内的流动换热实验数据对数学模型进行验证。其中,文献[26]的翅片结构(结构1)为h=6.5 mm,s=2.1 mm,δt=0.3 mm;文献[27]的翅片结构(结构2)为h=10.287 mm,s=4.089 4 mm,δt=0.254 mm。计算值与实验值的对比结果如图5所示,j因子的计算值与文献[26]和文献[27]的实验数据的平均相对误差分别为8.7%和27.6%;f因子的计算值与文献[26]和文献[27]的实验数据的平均相对误差分别为13.8%和10.7%,因此翅片通道内流动换热的数学模型与实验值的误差在合理误差范围内。

图5 平直翅片内流动换热计算值与实验值结果对比

2.3 氢正仲转化反应

为了验证已有的正仲转化反应动力学模型的正确性,对Elovich计算模型[15,21]、Langmuir-Hinshelwood计算模型和一阶计算模型[23]等3种模型分别进行验证。3种模型计算值与Hutchinson等的实验数据[22]对比结果如图6所示。压力p=0.206 85 MPa时,Elovich计算模型、Langmuir-Hinshelwood计算模型和一阶计算模型的平均相对误差分别为2.6%、15.8%和18.8%;压力p=0.420 595 MPa时,Elovich计算模型、Langmuir-Hinshelwood计算模型和一阶计算模型的平均相对误差分别为0.6%、30.7%和22.4%;压力p=0.841 19 MPa时,Elovich计算模型、Langmuir-Hinshelwood计算模型和一阶计算模型的平均相对误差分别为2.8%、33.0%和23.4%;压力p=1.654 8 MPa时,Elovich计算模型、Langmuir-Hinshelwood计算模型和一阶计算模型的平均相对误差分别为1.2%、33.6%和23.5%。因此,Elovich计算模型在计算范围内的平均相对误差为1.8%,是已有的氢正仲转化动力学模型中与实验数据吻合最好的计算模型。

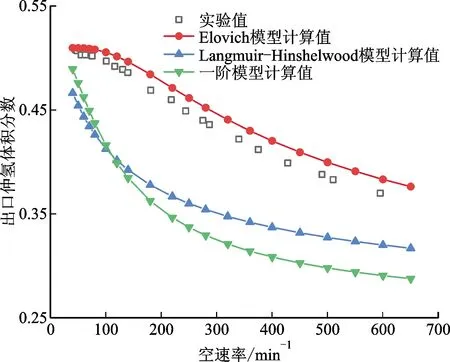
(a)p=0.206 85 MPa,T=76 K

3 结果分析

3.1 连续正仲转化性能分析

为了保证液氢的安全储运,要求液氢中的仲氢体积分数大于95%[7,28],考虑到氢正仲转化反应程度和设备成本,本文以出口仲氢体积分数为平衡仲氢体积分数的95%作为标准。当热侧Re=1 000、l=2.5 m时,热侧出口温度为43.7 K,冷侧出口温度为66.8 K,以44 K的平衡仲氢体积分数0.843 2的95%为标准,此时热侧出口仲氢体积分数为0.812 7,能够满足出口仲氢体积分数要求。冷热侧轴向的温度分布如图7所示。冷热侧的流体采用逆流布置方式,冷热侧的整体温度变化规律一致。以隔板温度作为中间温度,冷热侧的温差变化规律一致,沿轴向呈先下降后上升的变化趋势;热侧入口处温差较大的原因是热侧氢气刚进入催化层,催化剂颗粒使换热能力得到极大的提升,热侧氢气温度快速下降;冷侧入口处温差较大的原因是该位置热侧的氢气比热急剧上升,从而使冷侧氢气的温降加快。冷侧压降约为36.3 Pa,而热侧因为催化剂颗粒的作用,压降达到了4 996.3 Pa。

图7 冷热侧轴向的温度分布

采用翅片通道的流动换热评价标准进行分析,热侧:j=0.022 80,f=18.867 77,F=0.008 56;冷侧:j=0.002 48,f=0.012 75,F=0.010 63。热侧j因子约为冷侧j因子的9.2倍,传热过程的主要热阻在冷侧;虽然热侧f因子远远大于冷侧f因子,但实际上热侧换热增强因子可达到冷侧换热增强因子的8%,由此热侧流体的综合流动换热性能与冷侧相近,正仲转化与流动换热一体化技术能够使设备在保证流动换热性能的同时完成连续正仲转化过程。热侧轴向方向的仲氢体积分数分布如图8所示,沿轴向方向上平衡与实际仲氢体积分数均呈近似线性上升的趋势,同时两者体积分数差在0.032附近波动,呈两侧高、中间低的分布规律,结合图7可知,这是由于两侧的换热温差变化变大导致的。

图8 热侧氢气轴向的仲氢体积分数分布

3.2 运行工况和翅片长度的影响

运行流量和翅片长度是影响氢气正仲转化和流动换热过程的重要因素,选择热侧Re=500～1 500和l=1.0～4.0 m进行相应的计算。冷热侧翅片通道内的流动换热指标j因子、f因子和换热增强因子F的变化如图9所示。根据图9可知,冷热侧j因子、f因子和换热增强因子均随着热侧Re的增加而降低,并且翅片长度越短变化速率越快;冷热侧j因子和换热增强因子随着翅片长度的增加而降低,并且热侧Re越小变化速率越快,而f因子随着翅片长度的增加而缓慢增加。在计算条件范围内,热侧j因子是冷侧j因子的8～10倍,该值随着热侧Re和翅片长度的增大而减小,当Re=500和l=1.0 m时,热侧j因子为0.040 26,是冷侧j因子的10.0倍;当Re=1 500和l=4.0 m时,热侧j因子为0.015 49,是冷侧j因子的8.2倍。在计算条件范围内,热侧换热增强因子达到冷侧换热增强因子的68.9%～94.2%,该值随着热侧Re和翅片长度的增大而减小,当Re=500和l=1.0 m时,热侧换热增强因子为0.014 36,达到冷侧换热增强因子的94.2%;当Re=1 500和l=4.0 m时,热侧换热增强因子为0.005 93,达到冷侧换热增强因子的68.9%。因此,对于氢正仲转化和流动换热一体化设备,在保证正仲转化和换热要求的前提下,应优先考虑选用低Re的运行工况和短的翅片长度。

(a)j因子

出口仲氢体积分数随运行工况和翅片长度的变化如图10所示。当翅片长度一定时,出口仲氢体积分数随着热侧Re的降低而上升,并且翅片长度越短变化速率越快;当热侧Re一定时,出口仲氢体积分数随着翅片长度的增加而上升,并且热侧Re越大变化趋势越明显。热侧Re减小会减小进入翅片通道内的氢气质量流量,同时翅片长度增加会增加翅片通道内催化剂的体积,两种方式均会增加氢正仲转化反应的程度,使出口仲氢体积分数增加。参考文献[22]中空速率的概念,为了综合反映氢气质量流量和催化剂的体积对出口仲氢体积分数的影响,引入质量空速率GV

图10 出口仲氢体积分数随运行工况和翅片长度的变化

(22)

式中,m为入口质量流量,kg/s;V为催化层体积,m3。如图11所示,在计算条件范围内,出口仲氢体积分数与质量空速率近似呈线性变化趋势。将计算数据进行线性拟合

图11 出口仲氢体积分数随质量空速率的变化

(23)

拟合关联式与计算数据的拟合度为0.987 4,平均相对误差为0.27%。根据拟合关联式计算,42～70 K计算工况内,当质量空速率GV≤0.658 kg/(m3·s)时,出口仲氢体积分数能达到要求。

4 结 论

本文以氢液化流程中两股流板翅式换热器为研究对象,研究了42～70 K温度区间内氢气在催化剂填料的平直翅片通道内正仲转化反应与流动换热的耦合过程,得到结论如下。

(1)对比分析了已有的氢正仲转化动力学模型,发现Elovich计算模型的平均相对误差为1.8%,是与实验数据吻合最好的计算模型。

(2)计算工况范围内,热侧j因子是冷侧j因子的8～10倍,传热过程的主要热阻在冷侧;热侧换热增强因子达到冷侧换热增强因子的68.9%～94.2%,正仲转化与流动换热一体化技术能够使设备在保证流动换热性能的同时完成正仲转化反应。

(3)对于氢正仲转化和流动换热一体化设备,低Re的运行工况和短翅片长度的流动换热性能更好。

(4)42～70 K计算工况内出口仲氢体积分数与质量空速率近似呈线性变化趋势,当质量空速率小于等于0.658 kg/(m3·s)时,出口仲氢体积分数能达到要求。