讲究算理教学策略?提升学生计算能力

陈晓征

【摘 要】计算能力是学生应具备的基本素养之一，提高学生的计算能力应加强算理教学。算理是算法的基础，教师不仅要教会学生计算，更应该让学生明白算理、巩固算法，在教学中要关注学生的生活经验，讲究算理教学策略，注重以做悟理、以经验探理、以比显理、以联识理、以用思理，实现真正意义上升华算理、算法，进而提高学生数学思考力和计算力，促进学生计算能力与素养的提升。

【关键词】小学数学 计算算理 计算能力 教学策略

计算在小学数学教学内容中的比重非同一般，计算能力是学生应具备的基本素养之一。计算能力好比学习数学漫漫长路中的“双脚”，计算能力强，可以让学生在学习数学的“长跑竞赛”中遥遥领先，反之，就会拉开差距。据了解，教师教学过程也有多种误区，往往有教师觉得学生只要学会计算，再通过一遍又一遍的重复练习自然就会形成技能，结果却不容乐观，学生的计算仍屡屡出错。究其原因，还是学生对计算算理的理解不够，只是课堂上蜻蜓点水般的走过场，学生吃不透算理、理不清缘由、说不出道理。针对这种现象，本校积极开展“小学数学算理教学的实践与研究”的课题研究，在研究与实践中发现，教师不仅要走出轻视算理教学的误区，更要讲究算理教学策略，从而有效促进学生计算能力的提升。

一、以做悟理，让算法有形

小学数学计算内容较多，要说清为什么这样算的道理，较为抽象，而且对于小学阶段的學生来说，他们又以形象思维为主。在厘清算理、形成算法的教学过程中，有些教师往往会忽视算理教学环节，简单粗略地一笔带过，偏重于归纳算法，这会导致学生的学变得枯燥、无趣，理解也不透彻，只观其表，而未知其理。数学家华罗庚说过，数缺形时少直观，形少数时难入微。所以在教学中，教师要抓住学生思维方式中的形这个“中介”，让学生在直观的操作中明白怎么算、为什么这样算、计算时要注意什么，形成丰富鲜明的数学表象，让抽象的算理变得直观而形象，使学生经历算理由形到理的建构。

例如，在教学“两位数减一位数的退位减法”时，教师先让学生从图中获得信息，并列出算式“36-8”，再给学生充分的时间和空间，用“学习小帮手”——小棒摆一摆，让同桌互相交流摆的过程，最后汇报怎么减的方法。许多学生想上台展示摆法，于是教师让同桌的2个小搭档上台展示汇报。

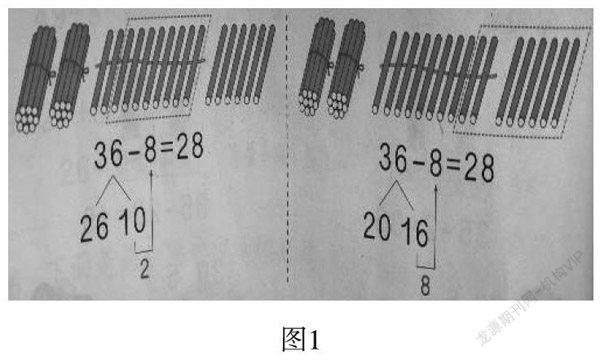
出示学生作品（如图1）：

生1：先摆3个整捆的，也就是30，再摆另外的6根，合起来就是36，6不够减8，拆一捆，和6合起来就是16了，先算“16-8=8”。十位的3捆，因为刚刚拆了一捆，所以剩下2捆了，也就是只有20了。

师：结合摆的小棒图讲得很清楚，然后怎么算就可以了？

生2：我知道，接着算“20+8=28”就可以了。我的方法和他的不同，我要开始讲了，大家看过来。（全班所有的眼神都注视着这位小老师了）

生2：我喜欢用一捆10根先减8等于2，2根再加上还有的 26根，就是28根。

师：不错。都有道理。

在这个教学过程中，学生充分借助小棒动手操作摆一摆，并圈一圈，让怎么减的方法清晰明了地呈现在眼前。直观演示让算法逐渐清晰，使学生很快明白了先算什么、再算什么，让算理摸得着、看得清，其中的算法自然水到渠成——当个位不够减，向十位退一当十再减。直观演示使学生的学变得有趣，课堂氛围更加灵动，学生能真正领悟算理、掌握算法。

二、以经验探理，让算法显质

数学算理是数学的灵魂，也是本质所在。数学算理的本质是探索和挖掘，既不像有些教师那样，按部就班地、凭教师过多的言语讲授传给学生，也不是让学生过多地模仿和记忆。学生有自己的生活经验、知识基础和见解，他们是学习的主人。教师只有引导学生展开数学算理探究活动，让学生借鉴经验、抓住已有知识和新学计算的联系和生长点，才能促使学生积极主动地探究计算的算理，挖掘算法的本质。

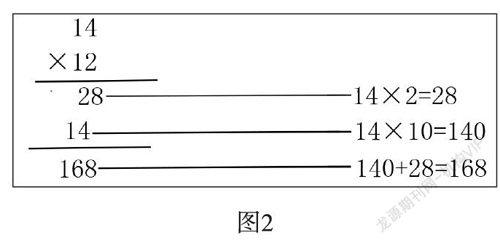
例如，教学“两位数乘两位数的笔算乘法”时，教师从学生已经掌握的两位数乘一位数、整十数的口算乘法以及两位数乘一位数的笔算乘法的知识基础入手，在开火车口算“21×3=”“12×4=”“14×10=”等算式和笔算“14×2”后，唤起了学生的计算经验。当遇到算式“14×12”时，学生结合点子图圈一圈、分一分，就能很快发现可用先分后合的方法，即转化成学过的“14×10”和“14×2”来算，再把俩乘积相加，“140+28=168”。紧接着，教师再问：“你能把横式的计算过程，变成竖式计算吗？”引发学生对笔算乘法的深入探索。学生交流展示笔算竖式，再通过连一连，联系横式的计算过程。（如图2）

学生的尝试理解由浅显转入深入，逐渐发现笔算乘法竖式和横式的计算过程是一样的。教师在计算的易错点、关键处设问：十位上的1乘4的积是4，4为什么要写在十位上？140的个位的0为什么可以不写？让学生在思考与交流中，探明写在十位上的4就表示40，140的1和百位对齐，个位上的0可以简洁地省略不写的道理。学生只有明白了为什么要这样做，才能够深刻理解算理，轻松建构算法。

三、以比显理，让算法有移

计算内容遍布广，算理也如影随形，无处不在。计算教学中的算理并不是孤立存在的，算理之间形成一个有联系的知识系统，存在一定的关联性，跨度时而大、时而小。因此在教学中，教师应充分引导学生把握计算算理之间的内在联系。常用的比较教学法，是一种行之有效的方法，在观察比较中发现算法的共同点、算法的细微不同处、算法的优势，从而让学生深入理解算理、算法。久而久之，学生必定能灵活运用算法，实现认知和算法迁移学习的持续发展。

下面是一位教师教学“9加几”时的教学片段：

师：很不错，同学们学会了“9加几”多样化的计算方法。会用数数的方法、接着数的方法和“凑十法”计算。

师：同学们学会了“9加几”的计算方法，你能把“9加几”的所有算式按顺序排一排吗？

生（齐）：能。

（学生说算式，教师板书，如图3）

9+1=10               9+4=13              9+7=16

9+2=11               9+5=14              9+8=17

9+3=12               9+6=15              9+9=18

师：仔细观察和比较，和的个位比第2个加数少几？你发现了什么？

生：少了1，看，0比1少1，1比2少1，2比3少1。

师：同学们都发现了，接下来一起说一说。

生：3比4少1，4比5少1，5比6少1……

师：少的1哪里去了？

生：和9凑成10了。

师：同意吗？同意的一起说。

生：少的1和9凑成10了。

师：比较数数的方法、接着数的方法和“凑十法”，你喜欢哪种方法呢？

生1：喜欢“凑十法”，看到9，就想到另一个数少1，又快又准。

生2：用数数的方法比较麻烦，我也喜欢“凑十法”。

全班同学都喜欢用“凑十法”计算，其实“凑十法”是把20以内的进位加法转化成学生所熟悉的十加几的方法，从而化难为易。紧接其后学习的8、7、6加几，引导学生串联比较，发现规律：看到8，另一个数少2;看到7，另一个数少3;看到6，另一个数少4……少的数都用来凑十啦。同学们都会感叹： “‘凑十法太好了，太喜欢了，它让我们的计算又快又准。”学生在多次比较中真切感受到这一算法的合理性，从而促进算法优化，最后形成计算技能，提升计算能力。

四、以联识理，让算法有通

数学计算知识由易到难，不同年級有不同的要求，虽有不同，却是一个富有层次性、连贯性、整体性的学科内容。孤立的教学，只会停留在单独的封闭的狭隘空间，不利于透彻清楚地厘清算理在各个年级、各个阶段之间的关联，不利于学生构建知识结构网络。所以数学教学最忌讳孤立、割裂、碎片化的教学。本校开展课题研究以来，笔者在教学中深有体会，教学既要有“分”中独立的学习探究，又要有“合”中巧妙的知识串联，如此才能真正实现算理之间互相联通、关联，实现数学算理、算法认知的整体效应。

下面是一位教师教学“小数加减法”时的教学片段：

师：大家对小数的计算有了一些了解，再看看这个问题（如图4），想一想，可以怎么算？用自己喜欢的方式算。

算一算：某商店里，一支笔卖1.45元，一个笔盒卖7.8元，买一个笔盒和一支笔共花多少钱？

生1：7.8元是7元8角，1.45元是1元4角5分，可以化成元角分来计算，7元8角+1元4角5分=9元2角5分。

生2：可以化成整分来计算，转化为整数加法来计算，780分+145分=925分，算起来也很快。

生3：我尝试用小数来计算，7.8元+1.45元=9.25元。

师：这些方法都有道理。对比上面三种算法，进行思考和讨论——我们在计算时要注意些什么？

探究多样化的计算方法后，教师引导学生交流讨论，让学生进一步感悟“相同单位的数才能直接相加减”的算理，把整数加法的算法和小数加法联系起来，使学生形成对整数加法算理和小数加法算理的认知共鸣，达成共识——“计算对位法都是相同的”，进而完善学生的数学计算算法知识系统。

五、以用思理，让算法有意

学生理解算理、掌握算法的最终目的就是学以致用。教师要通过形式多样的练习，让学生在练习思考中活用算理和算法，形成举一反三的能力，不断提升计算能力。

例如，教学“笔算乘法”时，教师以例题中的看书为情境，设计一题多练，由易到难，层层递进，引导学生在算一算、说一说、议一议中运用本节课学习的“两位数乘两位数”的算理去思考解决问题，逐渐形成计算技能，学生的计算、推理和思维能力也有所提升。

王老师买了一本书，如果每天看12页，13天能看多少页？

1. 算一算：列竖式计算。

2.说一说：不列竖式，你能通过第1题算出的结果，推理出23天看多少页吗？说说你的想法。

10天看的页数：12×10=120（页）;23天看的页数：156+120=276（页）。

3.议一议：如果每天看1□页，计算22天看多少页的竖式（如图6）。

（1）A与B谁多？

（2）A与B相差几个几？

（3）A、B、C是什么关系？

总之，算理是算法的基础，教师不仅要教会学生计算，更应该让学生理解算理、掌握算法。在教学中，教师要关注学生的生活经验，讲究算理教学策略，注重以做悟理、以经验探理、以比显理、以联识理、以用思理，实现真正意义上的升华算理、算法，进而提高学生数学思考力和计算力，促进学生计算能力的基本素养的提升。

【参考文献】

[1]张华丽.小学数学计算教学中算理算法的教学策略[J].数学教学通讯，2020（16）.

[2]周存劳.核心素养下小学数学口算教学策略初探[J].读与写，2019（7）.

注：本文系2020年度福建省上杭县立项课题“小学数学算理教学的研究与实践”（编号：XX2020SX06）的研究成果。