随机车轮不圆顺及车辆参数对轨道频域振动响应影响分析

李明航，马 蒙，谭新宇，张厚贵，刘卫丰

(1.北京交通大学 土木建筑工程学院，北京 100044；2.北京市劳动保护科学研究所，北京 100054)

地铁列车诱发的振动主要由准静态激励和动态激励产生。其中动态激励的产生机制包括：车轮不圆顺和轨道不平顺、轨道节疤和车轮扁疤、多边形磨耗等引起的激励，以及周期性轨道结构的参数激励等[1]。因此，振动响应大小与列车状态、线路类型、钢轨状态及轮轨养护维修水平等直接相关。

通过统计分析大量的现场测试数据，李宪同等[2-3]发现同一测试断面一天内多趟列车引起的隧道壁振动响应呈现明显的离散特征，最大Z振级相差超过5 dB；马蒙等[4]发现同一列车车轮镟修后，隧道壁振动响应在环境振动关心的20 Hz～80 Hz内平均衰减量超过10 dB。究其原因，针对某一固定测试断面，在较短时间内虽然车速、车型和线路条件等基本一致，但由于不同列车状态等，导致了短时间内的多列不同列车通过引起的频域振动响应呈现显著的不确定性，且不同频段的离散特征差异显著[5]。列车状态差异具体可分为车辆参数差异(如载质量波动、车辆悬挂系统老化及制造误差等)及车轮不圆顺的差异。目前针对该问题的研究仍以统计分析大量现场实测数据为主，对于其离散原因、不同频段的控制因素等机理性研究并不充分。

列车运行引起的振动响应是典型的随机过程。在理论研究方面，考虑随机激励或结构参数随机性引起的随机振动问题主要采用随机模拟[6]、随机摄动理论[7]、正交展开理论[8]、概率密度演化理论[9]等方法。在车-桥耦合、车-轨耦合随机振动分析领域，余志武等[10]应用概率密度演化理论，分析了车辆参数随机性的车桥竖向随机振动；徐磊等[11]分析了高速铁路轨道概率不平顺谱、车轮磨耗发展引起的车轨耦合随机振动问题；项盼[12]分析了固定输入不平顺谱激励作下，车辆随机参数引起的车轨耦合随机振动响应。但诸类研究主要从车辆运行安全性、乘客舒适性等角度出发，重点分析车-轨耦合系统振动响应的时域随机特性，且未见考虑车轮不圆顺随机性对车-轨耦合系统的频域振动响应影响分析。

随着轨道交通运营引起的振动及噪声问题愈发凸显，尤其是针对已开通线路，在无法实施更换减振、降噪产品的条件下，通过制定合理的列车养护维修策略等手段降低振动及噪声影响的技术潜力值得深入挖掘。针对该问题首先应给出不同列车车轮磨耗水平及参数随机性对车-轨耦合系统的频域振动响应影响的理论分析结果。

本文通过实测不同运营里程典型列车车轮不圆顺，构建随机车轮不圆顺谱；测试某一地铁隧道区间轨道高低不平顺、钢轨表面粗糙度及轨道振动响应；基于车-轨耦合频域解析模型，以输入实测轨道不平顺谱耦合随机车轮不圆顺谱作为激励，采用随机模拟法，详细分析了随机车轮不圆顺及车辆参数对轨道频域振动响应影响。

1 车轮不圆顺测试及其随机谱构建

1.1 实测车轮不圆顺

车轮不圆顺测试列车为6节编组的地铁B型车。选取测量的4列典型列车累积运营里程数分别为10.6万km(Ta车)、11.3万km(Tb车)、14.1万km(Tc车)及15.5万km(Td车)，且均未开展过车轮镟修作业，标准车轮半径为0.42 m。采用TriTops车轮不圆顺测试仪对全车所有车轮进行现场测试，该仪器具备3个等距测量探针，可同时测量距离轮缘外侧70 mm的名义滚动圆处及其左右10 mm处，3个不同车轮踏面位置的不圆顺，如图1所示。

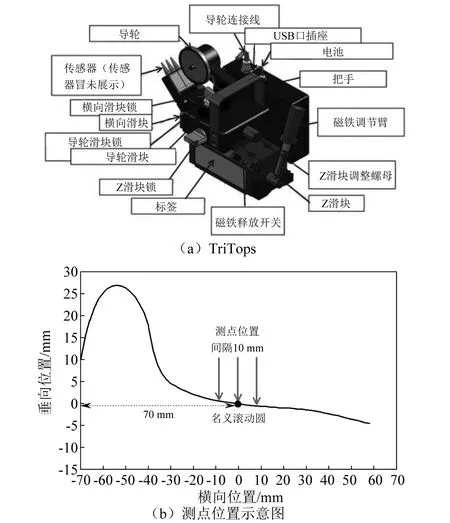
图1 测试仪器及测点位置

车轮不圆顺测试样本的功率谱密度函数(power spectral density, PSD)估计是构建其随机谱函数的基础，后文简称为车轮不圆顺谱。本文选用周期图法进行车轮不圆顺谱估计，对测试数据施加汉宁窗，为保证功率谱幅值的准确性，加窗恢复系数设为2[13-14]。

城市轨道交通引起的环境振动及结构二次噪声领域，重点关心200 Hz以下频段的振动响应。考虑以40 km/h作为下限运营车速，则重点关心波长大于50 mm。车轮不圆顺的上限影响波长为车轮周长(≈2.62 m)[15]。因此，本文给出的车轮不圆顺谱统计结果均只反映0.05 m～2.62 m波长范围。4列典型列车车轮不圆顺测试样本的PSD及其初步统计结果，如图2所示。在某些波长处，不同测试样本车轮不圆顺谱相差超过3个数量级；车轮不圆顺谱呈现与各阶多边形磨耗典型波长相对应的峰值；均值谱、5%及95%分位谱呈现相似的波动趋势，三条统计谱线间主要表现为量级的差异。

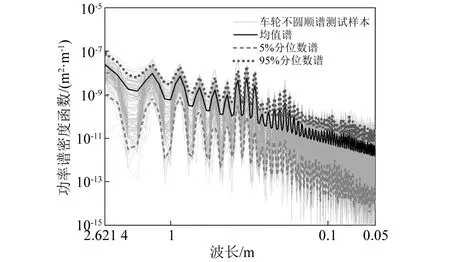
图2 典型列车车轮不圆顺谱测试PSD样本与分位数谱

韩鹏等[16]研究发现，随着运营里程的增加，车轮踏面的磨耗量呈现以实际滚动圆为中心的正态分布特征，单位运营里程车轮磨耗量同样呈现正态分布特征。因此，即使本文选取的列车无法反应车轮镟修全周期内的运营状态，但考虑运行线路整体线形，同一列车动车、拖车的轮对质量差异，同一车轮多个测量点等众多随机因素共同作用下，本文测得的车轮不圆顺谱基本可以反映整个车轮镟修周期内的大多数车轮不圆顺状态。以图2给出的样本为基础构建随机车轮不圆顺谱是合理的。

1.2 车轮随机不圆顺谱构建

遍历车轮随机不圆顺所有激励形态是分析其引起振动响应不确定性问题的关键。实测数据表明，车轮不圆顺表现为显著的多边形磨耗特征，车轮不圆顺谱在各阶多边形对应波长处出现明显峰值，且离散超过3个数量级。为了便于统计分析，将不圆顺谱转换为等效粗糙度级

(1)

式中：r0为参考值，1 μm；λ为关心波长范围内的不同波长取值；PSD(λ)为波长λ对应的功率谱密度值。

测试样本的等效粗糙度级样本及其均值、5%及95%分位数谱线统计结果，如图3所示，5%及95%分位数谱基本关于均值谱对称。

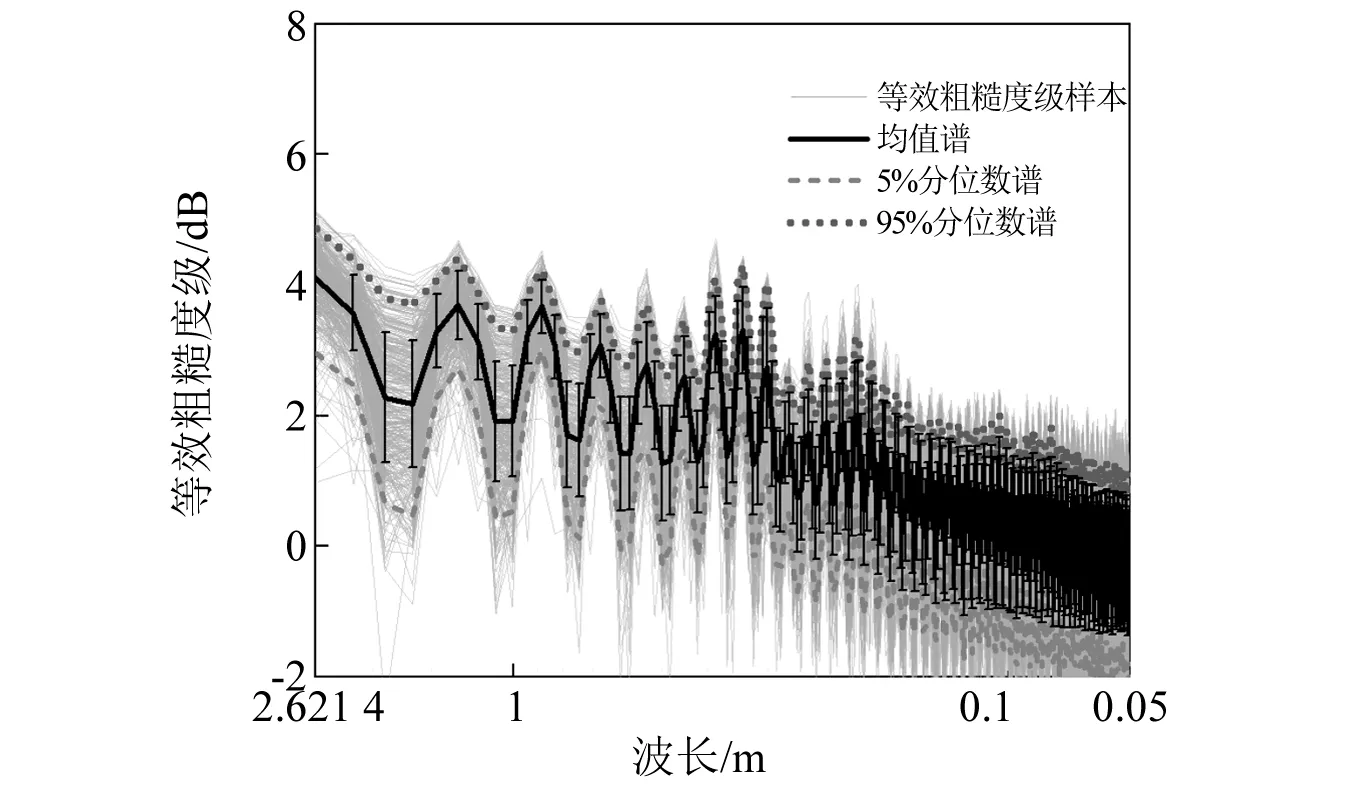
图3 测试车轮等效粗糙度级样本及分位数谱

图4给出了5阶～20阶多边形对应波长处的等效粗糙度级的统计分布规律。将功率谱转换为等效粗糙度级谱LPSD后，不同典型波长处的分布特征相似，呈现正态分布特征，且不同波长处的标准差基本一致。

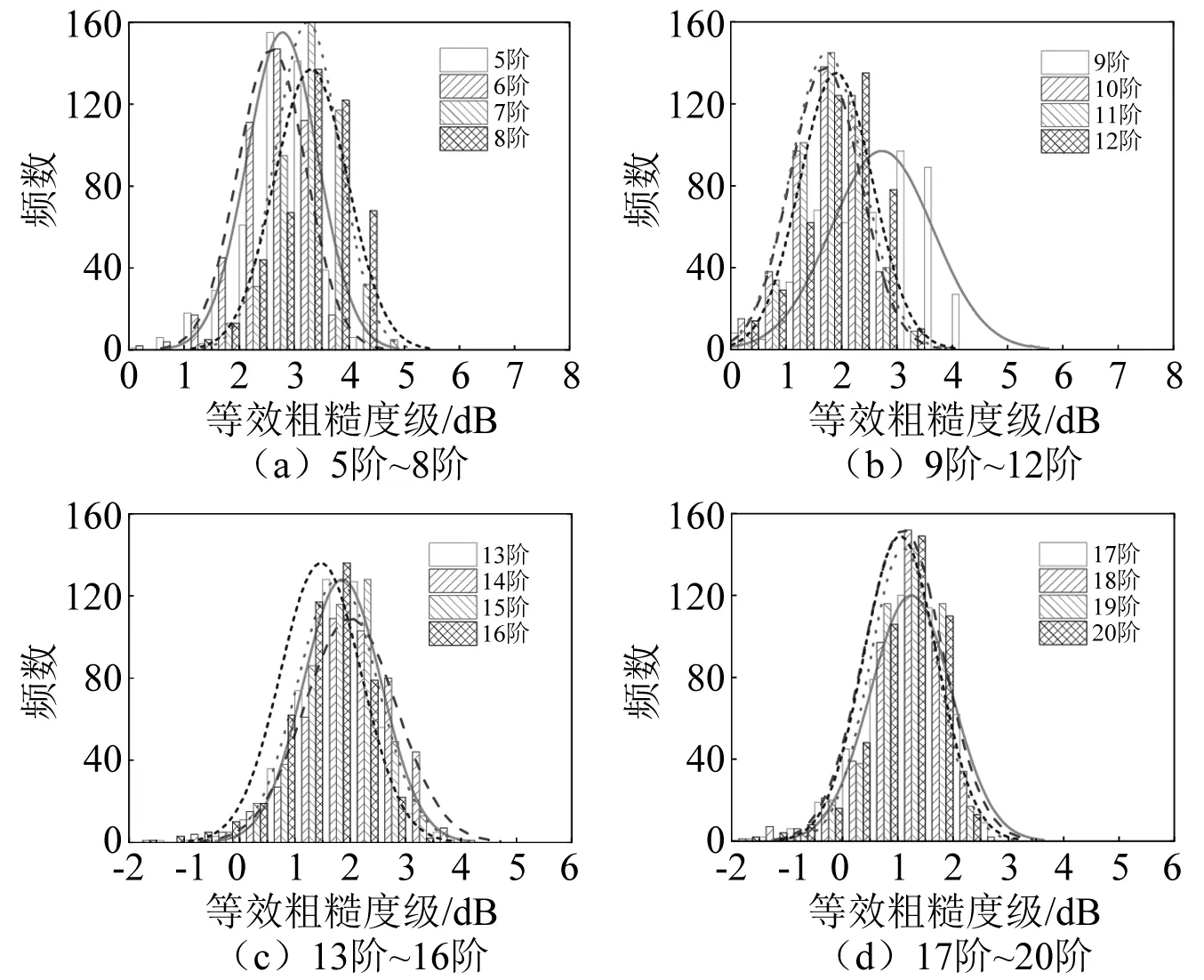
图4 典型多边形磨耗对应波长等效粗糙度级统计

假设车轮等效粗糙度级谱不同波长处具备相同的分布特征，在数值上只表现为均值μ(λ)的不同，标准差一致。以测试样本0.05 m～2.62 m波长段各个离散波长点对应的标准差为样本，其样本均值作为全波长统一标准差σtot，构建随机车轮不圆顺谱的概率密度函数

(2)

图5给出了等效粗糙度级及车轮不圆顺谱的5%及95%分位数的估计值与实测样本统计结果，在0.05 m～2.62 m波长范围内，估计谱与实测统计谱基本吻合，本文采用的估计方法可以较好地反应实测车轮不圆顺谱的分布特征。

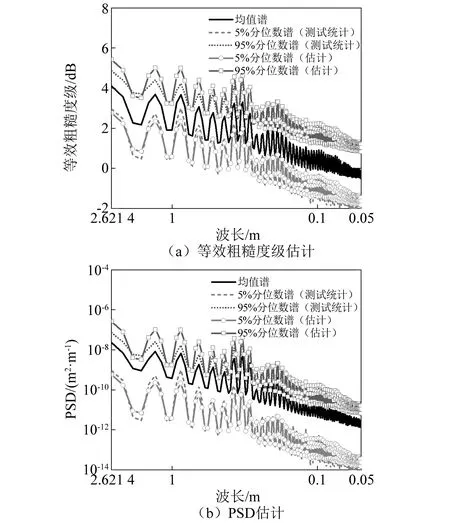
图5 车轮不圆顺实测分位数谱与估计分位数谱

2 频域车-轨耦合解析模型与模型校核

文献[17]提出的频域车-轨耦合模型，如图 6所示。具备力学概念明确、全解析、计算效率高等优点。本文采用该模型进行轨道频域振动响应的求解。

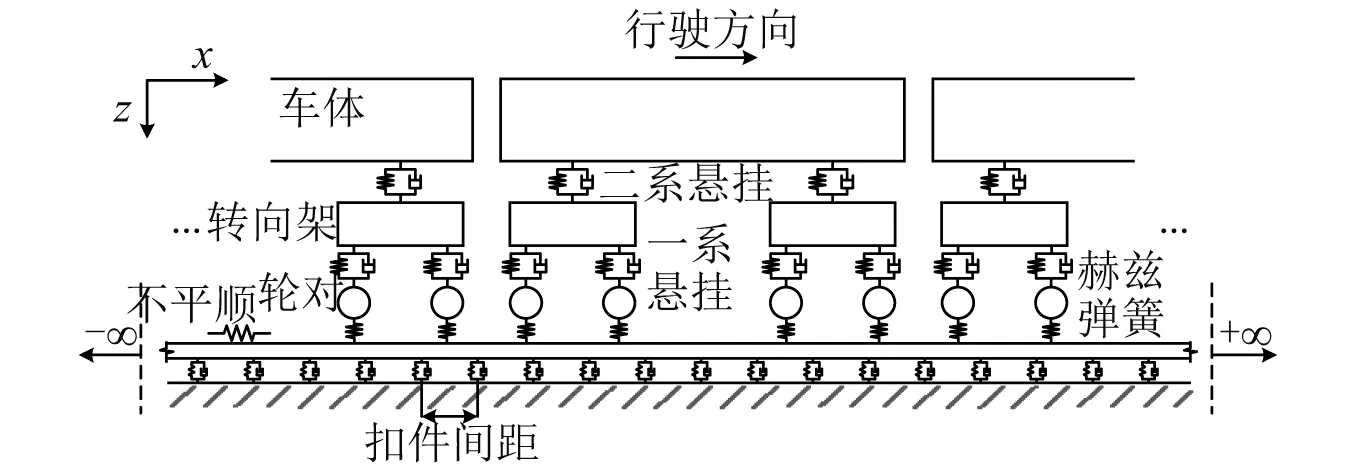
图6 DTVI2扣件轨道对应的车轨系统力学模型

2.1 车辆与轨道控制方程

计算模型参考地铁B型车，采取6节编组，单节车辆模型考虑为具备2系弹簧质量体系的10自由度2维模型，具体包括车体的沉浮及转动自由度、2个转向架的沉浮及转动自由度和4个轮对的沉浮自由度。各子结构均考虑为刚体，系统方程通过对各个刚体各自由度采用D’Alembert原理计算获得；轮轨间采用赫兹接触，接触参数见文献[18]；同时考虑轨道高低不平顺谱及车轮不圆顺谱作为系统激励。

列车第m节车辆的频域控制方程为

(3)

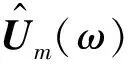
参考“无限-周期”理论[19-22]，将轨道结构视为以扣件间距L为周期的离散支撑无限-周期结构。钢轨简化为无限长欧拉梁，扣件支撑简化为弹簧阻尼单元。轨梁的振动响应可统一在一个特征周期长度内进行求解。在频域内，频率为ωl的单位移动荷载作用下，一个特征周期内的轨梁振动方程为

(4)

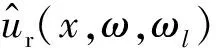
2.2 轮轨耦合不平顺谱拟合

为反应轮轨接触面的完整激励信息，需要同时考虑轨道动态不平顺、钢轨表面粗糙度及车轮不圆顺的全部激励能量。目前，轮轨耦合不平顺谱主要用于轮轨激励引起的滚动噪声问题，重点考虑轮、轨表面粗糙度的激励信息，主要形式分为三类：

(1)轮、轨分离谱[23]，即分别对车轮踏面及钢轨表面粗糙度谱进行测量估计，然后按照能量叠加的方式进行线性叠加。该方法完全不考虑车轮踏面粗糙度与钢轨表面粗糙度间的相干性，一定程度上会高估轮轨表面的实际激励信息。

(2)只考虑钢轨表面粗糙度。该方法显然会丢失车轮表面的激励信息。

(3)轮轨联合粗糙度谱[24-25]，该方法可通过现场测试列车通过引起的钢轨振动衰减规律等方式获得，体现了车轮踏面粗糙度与钢轨表面粗糙度间的相干性。

在轮轨相互作用过程中，由于列车轴荷载作用，车轮踏面与钢轨接触部分会出现局部弹性变形，形成半径5 mm～8 mm的椭圆形接触斑，其对于小于该尺寸波长段对应轮、轨粗糙度有明显的接触滤波作用，导致激励减弱。

为了保证激励信息的完备与激励能量的等效，采用不同波长处车轮及钢轨粗糙度能量叠加的方式，综合考虑轮、轨耦合激励作用。本文重点关注50 mm以上波长的轮、轨不平顺，远大于接触斑尺寸，因此可以忽略接触滤波效应。

轮轨耦合不平顺的拟合以马龙祥提出的改进三角级数拟合方法为基础，同时考虑车轮不圆顺及轨道不平顺的影响。该方法假设不平顺的样本函数由不同频率成分的谐波分量组成，且不同波长间相互独立。则列车第k轴历经的对应激励频率ωl(l=-NR,…,-1,1,…,NR)的轮轨耦合不平顺幅值可以表达为

(5)

(6)

S(Ωl)=SWheel(Ωl)+SRail(Ωl)

(7)

式中：S(Ω)为轮、轨耦合不平顺PSD；SWheel(Ωl)为车轮不圆平顺的PSD，SRail(Ωl)为轨道不平顺的PSD，定义在空间角频率区间[Ω1,ΩNR]上，该区间的选择依赖于感兴趣的频率范围和列车速度；ΔΩ和Ωl(l=1,2,…,NR)为将区间[Ω1,ΩNR]等分为NR个子区间后的子区间长度及各子区间的中心空间频率；θlk为不同轴之间0～2π内的随机相位。

2.3 模型验证

笔者在车轮不圆顺测试列车运营线路某单线隧道区间直线段，敷设DTVI2扣件普通整体道床轨道断面，进行了钢轨垂向振动加速度测试，列车运行速度约60 km/h。结合运营单位提供的线路运营信息，提取累积运营里程分别达到14.1万km列车(Tc车)及完成车轮镟修作业后1.2万km列车(Te车)引起的振动响应。两列典型列车引起的钢轨垂向振动加速度时程及频谱，如图 7所示。显然，Tc车引起的钢轨振动响应时程远高于Te车；频域内，50 Hz～400 Hz全频段内Tc车引起的钢轨振动响应时程远高于Te车，且在100 Hz附近具有一个与车轮14阶多边形磨耗直接相关的特征峰值。

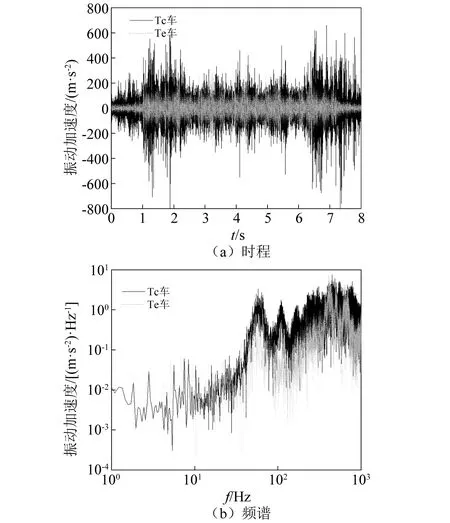
图7 典型列车引起钢轨加速度时程及频谱

参考测试断面的轨道参数及车辆类型，表1及表2分别给出了车-轨耦合模型的车辆及轨道建模参数。

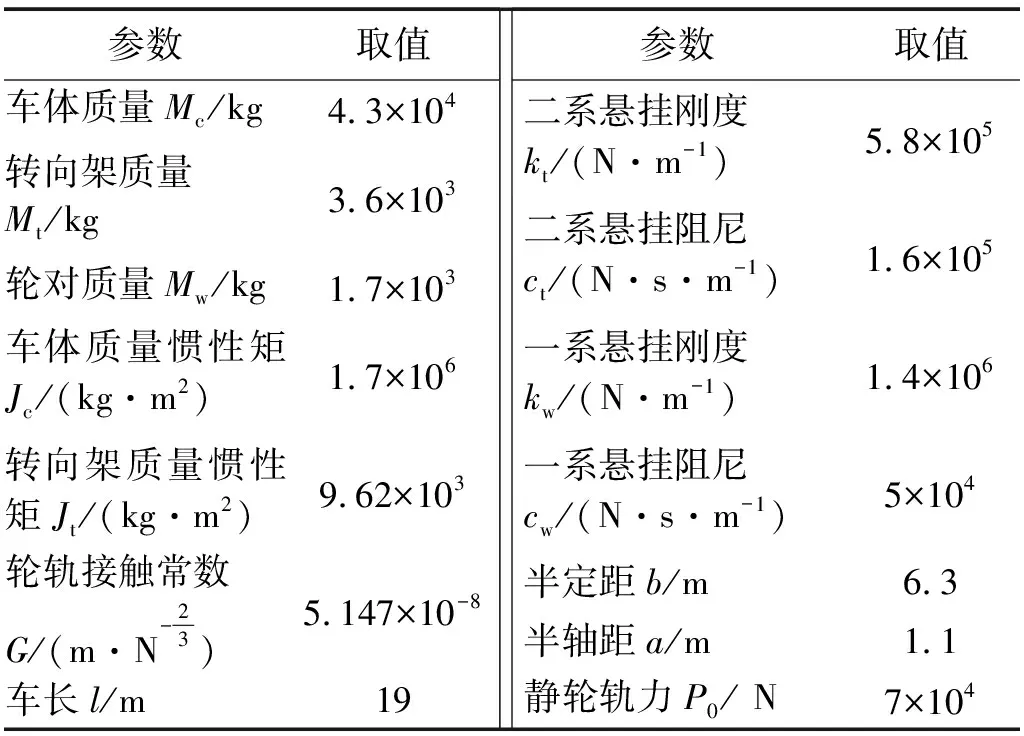
表1 地铁B型车关键参数

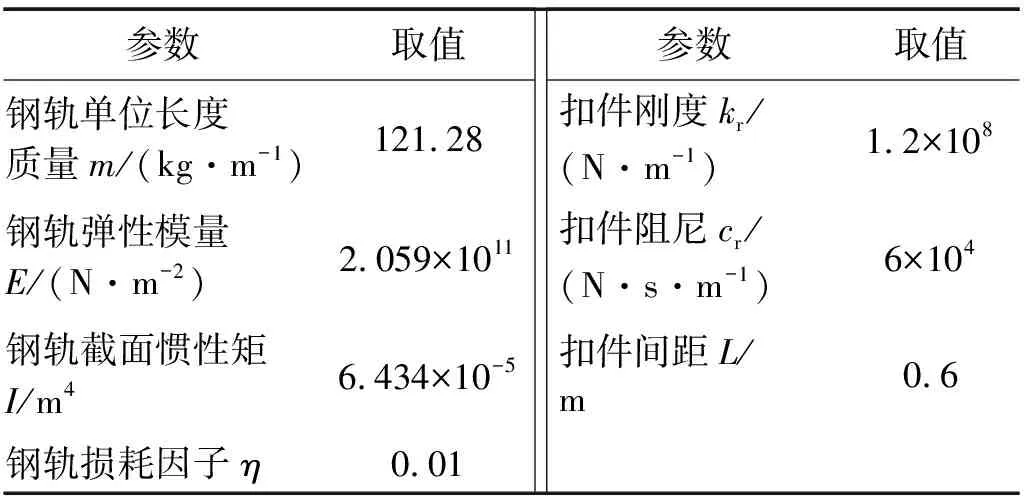
表2 DTVI2扣件轨道参数(对应两股轨道)

本文实测获得的轨道高低不平顺最短分析波长为2 m；钢轨表面粗糙度采用CAT小车进行检测，可获得3 m以下波长钢轨表面粗糙度。综合考虑测量数据的可靠性，模型输入的轨道不平顺谱分段采用测试区间实测轨道动态不平顺谱(≥2 m波长段)及钢轨表面粗糙度谱(<2 m波长段)；车轮不圆顺谱采用运营14.1万km对应的Tc车车轮不圆顺均值谱(≤2.62 m波长段)。轨道不平顺谱与车轮不圆顺谱作为联合激励，生成的轮轨耦合谱如图 8所示。<0.5 m波长段耦合谱的幅值主要体现为车轮不圆顺谱的幅值特征，≥0.5 m波长段体现为钢轨表面粗糙度谱及轨道动态不平顺谱的幅值特征。

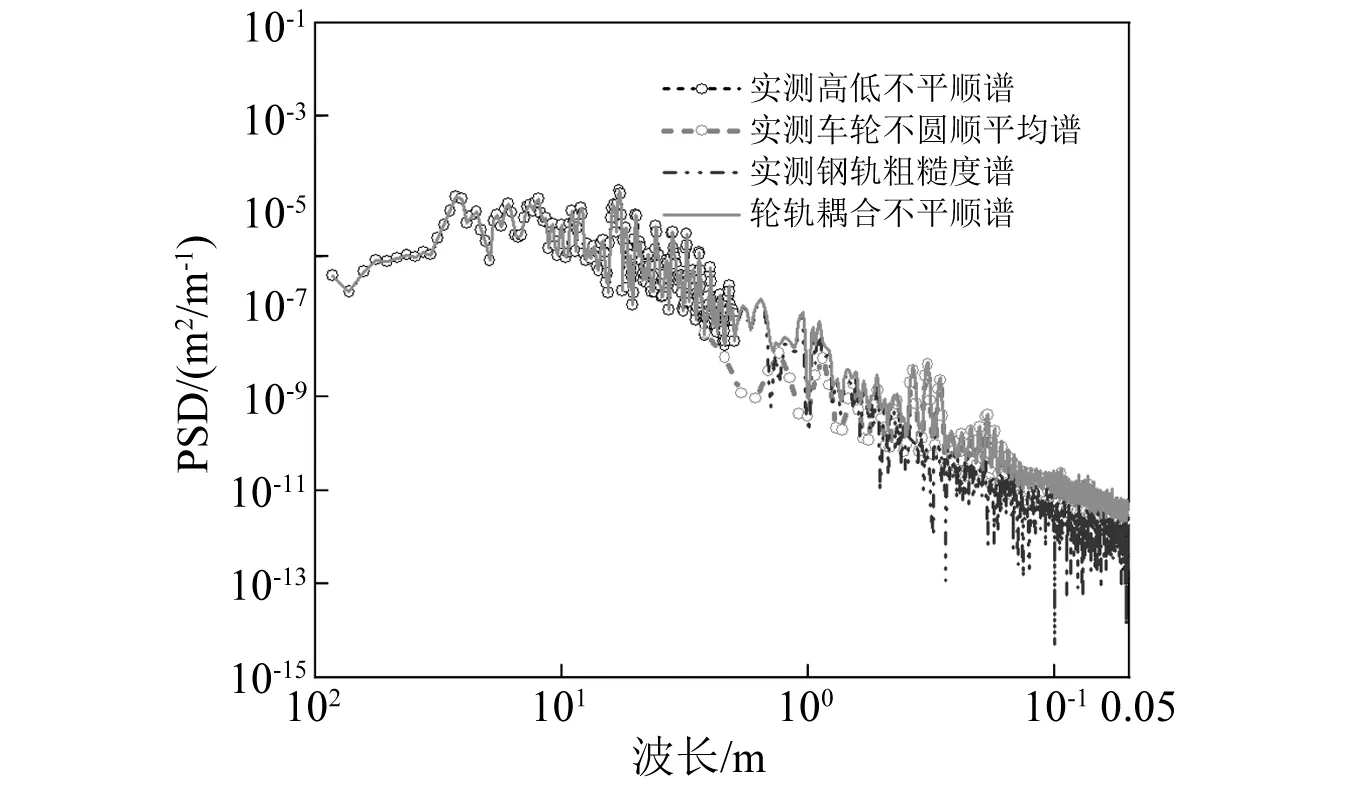
图8 Tc车轮轨耦合不平顺谱

振动加速度级定义为

(8)

式中：fi为第i个中心频率；a(fi)为第i个中心频率处的振动加速度有效值；a0为参考加速度值，10-6m/s2。提取典型列车(Tc车)通过引起的实测钢轨垂向振动加速度级对比模型计算结果，如图9所示。

平均绝对百分比误差(mean absolute percentage error，MAPE)可用于定量分析模拟计算结果与测试结果(约定真值)间的差异。MAPE是绝对误差与被约定真值之比，一般以百分数表示

(9)

式中：qi为计算值；Qi为约定真值；以计算值，真值形成一组数对，n为数对的个数。

如图9所示，计算结果与实测值在8 Hz～200 Hz全频段内吻合良好，大部分中心频率的分频加速度级位于实测数据的95%置信区间内，MAPE仅为2.4%。

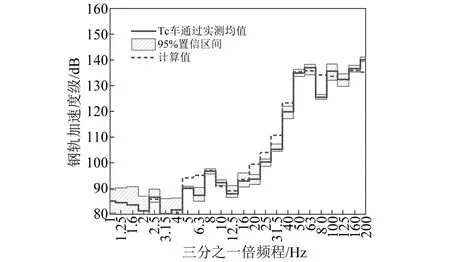
图9 实测典型列车通过与模型计算钢轨加速度级

3 随机不圆顺谱及随机参数对轨道频域振动响应的影响分析

除考虑随机车轮不圆顺激励外，同时考虑了随机车辆参数(载质量，一系悬挂弹簧刚度、阻尼，二系悬挂刚度、阻尼)对轨道频域振动响应的影响。各项随机参数的均值见表2，变异系数均设为5%。假设不同参数间相互独立，且服从正态分布。

基于协方差矩阵Cholesky因子分解的线性变换方法[26]，获得200组随机向量，进行随机模拟。计算工况分别考虑60 km/h，70 km/h，80 km/h及90 km/h，4个运行速度级。通过随机向量，生成的车轮不圆顺谱及轮轨耦合不平顺谱模拟计算样本，如图10所示。

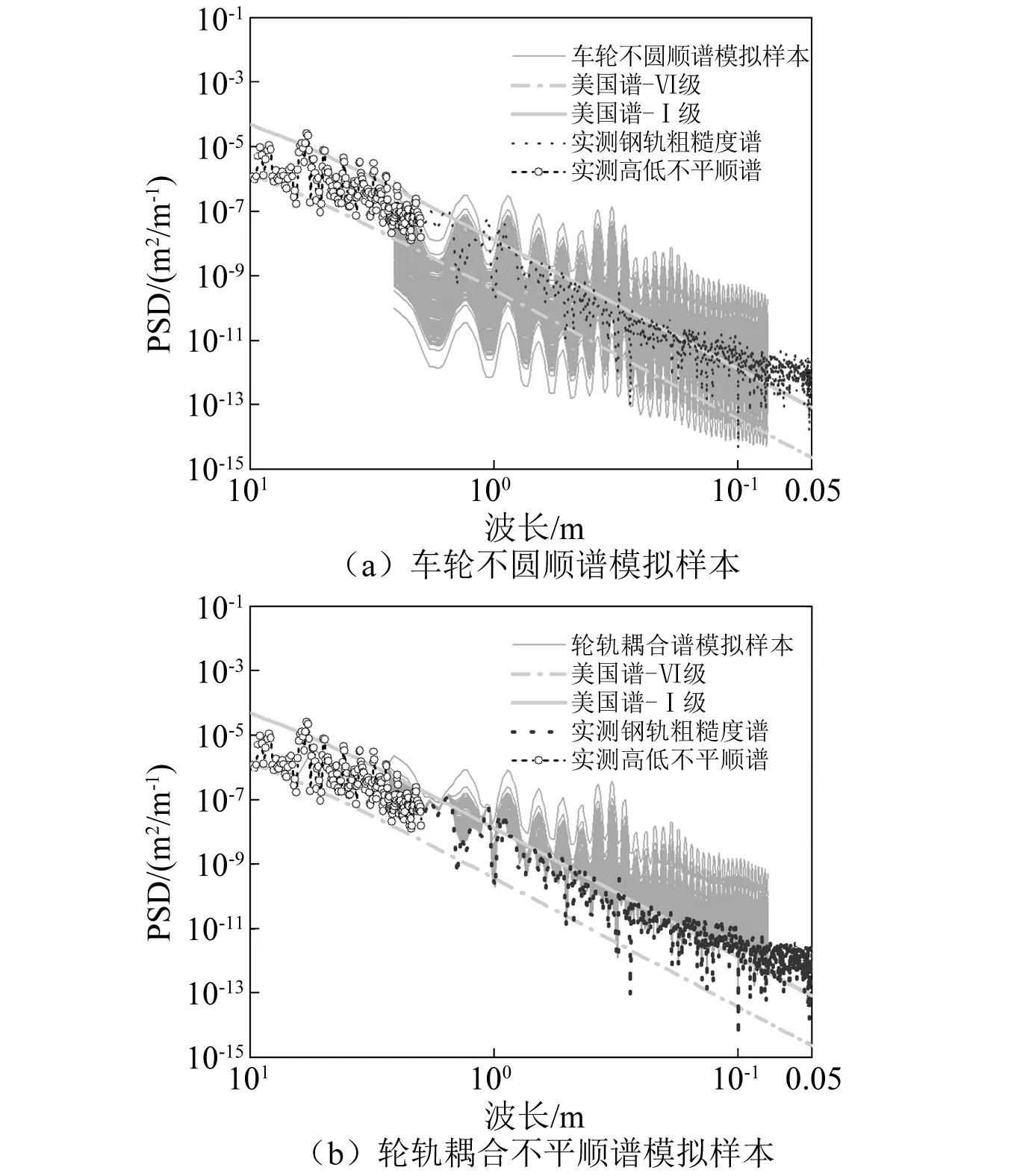
图10 轮轨耦合随机不平顺谱模拟计算样本

提取运营里程在10万km～16万km内的列车通过引起的实测钢轨振动加速度级与计算结果相比较。图11给出了60 km/h运行速度下计算结果与实测样本的均值及标准差。显然，在8 Hz～200 Hz全频段内计算均值与实测均值吻合良好，MAPE计算结果仅为2.1%；在12.5 Hz以上频段，计算结果基本可以包络实测结果，模拟计算加速度的标准差普遍更大。这是由于，在实际的车轮磨耗过程中，车轮踏面的磨耗量呈现正态分布特征，模拟计算的车轮不圆顺谱的分布特征由名义滚动轮及其左右10 mm的3个测量点的统计结果获得。因此，与实际的列车经过测试断面时历经的车轮不圆顺相比，本文采用的测试样本包含很多不圆顺的极端情况，数据覆盖范围更广。

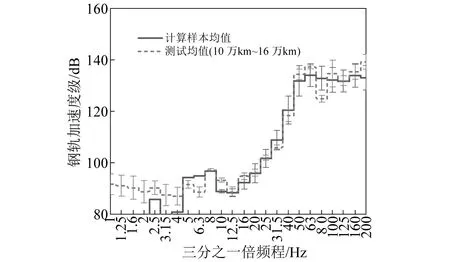
图11 计算值与实测值对比

图12给出了不同车速条件下的钢轨振动加速度级计算结果。随机车轮不圆顺谱导致，12.5 Hz以上分频加速度级显著离散，该频段的振动响应受动态激励控制；在车轮7阶～9阶多边形磨耗对应频段，即50 Hz～100 Hz频段内，分频振级离散超过20 dB；对于8 Hz以下频段，加速度响应受准静态激励控制，在车辆参数5%的变异系数条件下，并未导致该频段的加速度级出现明显的离散。

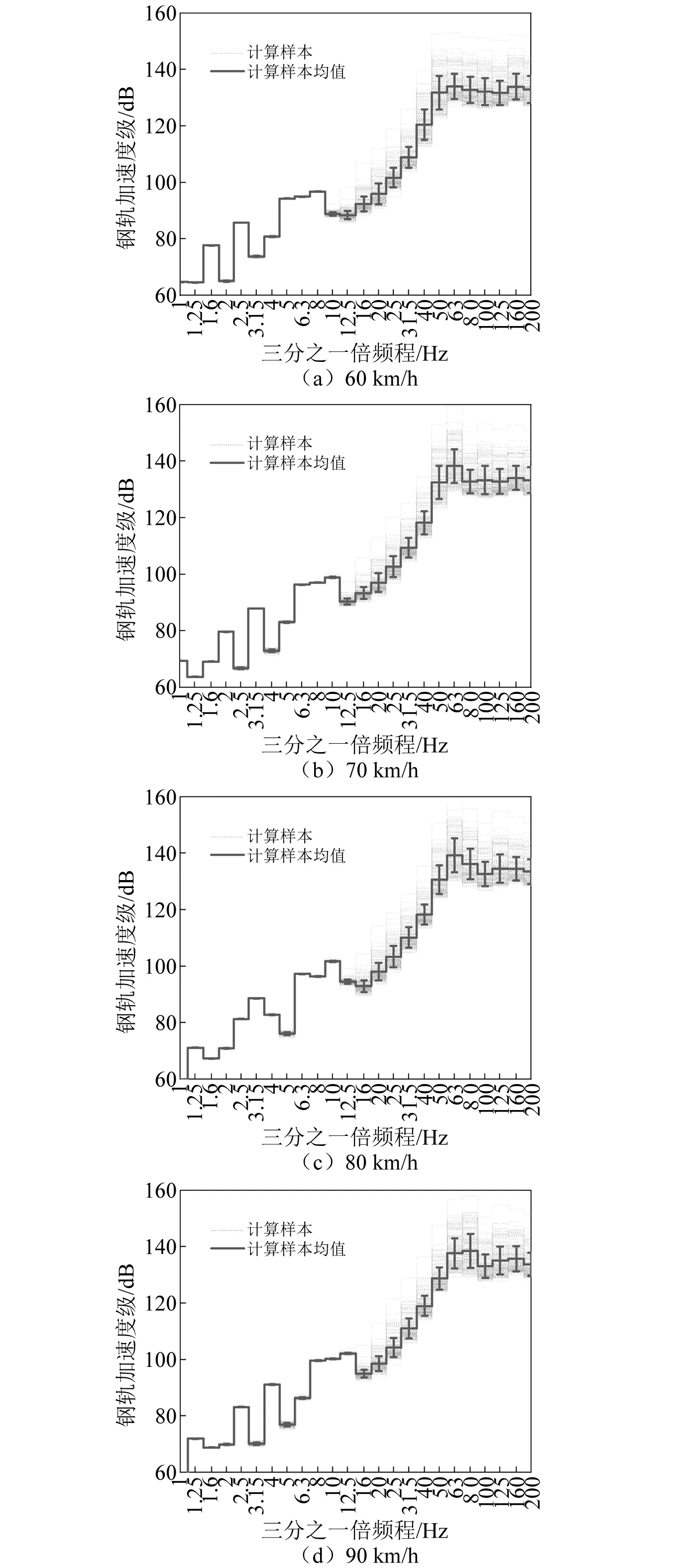
图12 钢轨振动加速度级模拟计算结果

图13给出了不同车速条件下中心频率25 Hz，40 Hz，63 Hz及100 Hz处的分频振动加速度级分布特征。不同车速条件下4个中心频率的振动加速度级均表现为明显的正偏态分布特征。该现象与输入的轮轨耦合不平顺谱直接相关。图 10(a)所示，通过车轮不圆顺谱概率密度函数生成的随机样本离散超过4个数量级，实测的钢轨粗糙度谱量级介于随机车轮不圆顺谱样本之间。二者叠加后，其能量较低的耦合不平顺谱主要表现为实测轨道高低不平顺谱及钢轨表面粗糙度谱的量级。因此，会出现大量接近轨道不平顺谱的轮轨耦合不平顺谱计算样本，从而导致钢轨振动加速度级计算结果呈现正偏态的分布特征。此外，随着车速的增加，与不同中心频率振动响应直接相关的典型轮轨耦合不平顺波长随之变化，分频加速度级并未表现出一致增加的趋势。

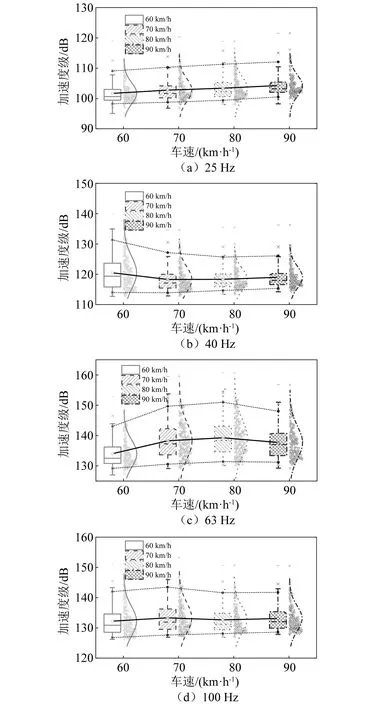
图13 典型频率钢轨振动加速度级模拟计算结果分布特征

4 结 论

通过实测不同运营里程典型列车车轮不圆顺，构建了随机车轮不圆顺功率谱密度函数的数学模型，并基于频域车-轨耦合解析模型，采用随机模拟法系统分析了随机车轮不圆顺及随机车辆参数作用下轨道的频域振动响应。研究结果表明：

(1)以轮轨耦合不平顺作为激励，输入车-轨耦合模型，在8 Hz～200 Hz全频段内计算均值与实测均值吻合良好，可获得准确的轨道系统频域振动响应；

(2)随机车辆参数、随机车轮不圆顺耦合轨道不平顺作用下，8 Hz以下的振动响应未出现显著离散；16 Hz以上的振动加速度离散明显，63 Hz以上频段差值超过20 dB，且在典型频率处均呈现正偏态分布特征。