混合框架可更换梁的抗震性能及设计方法
门进杰,王欢欢,兰 涛,3,任如月,史庆轩
(1.西安建筑科技大学 土木工程学院,西安 710055;2.西安建筑科技大学 结构工程与抗震教育部重点实验室,西安 710055;3.中国船舶重工集团国际工程有限公司,北京 100021)
可恢复功能结构(earthquake resilient structure,ERS),是指地震后不需修复或稍加修复即可恢复其使用功能的结构,又称功能可恢复结构。近年来,ERS逐渐成为抗震工程研究的热点[1]。由于ERS体系具有比传统抗震结构更高的抗震性能,现代抗震设计理念亟需从传统抗倒塌设防目标转向灾后可恢复功能目标[2]。带可更换构件的结构作为ERS体系中的一种,在地震作用下,通过可更换构件的塑性变形,集中耗散地震能量,保护主体结构不受破坏或只受轻微破坏,地震后不影响结构的使用,更换构件后结构全部恢复正常功能[3-4]。
近年来,国内外学者对可更换构件的研究主要集中于可更换耗能梁,如:Mansour等[5]针对偏心支撑的钢框架结构设计了一种可更换连系梁段;Lopes等[6]对钢连柱框架结构的试验研究表明,钢连柱中link破坏模式为剪切屈服时耗能最优;纪晓东等[7]对12个可更换钢连梁中端板-螺栓连接的消能梁段试件进行了拟静力试验,研究了梁段长度和加劲肋布置方式等参数对消能梁段的影响,并给出了设计建议;胡淑军等[8]针对短剪切型消能梁段,设计了108个考虑加劲肋间距、翼缘强度和跨高比等因素的模型,详细研究了短剪切型消能梁段的力学性能及各因素的影响规律。
虽然目前针对可更换钢梁进行了大量的研究,但是还存在几点不足,如:在地震作用下,端板与可更换钢梁的翼缘焊缝常会由于应力集中而开裂,无法充分发挥可更换钢梁的变形能力和耗能能力;可更换钢梁耗能能力虽然能得到充分发挥,但其震后修复的代价较高,可更换性较差。因此,可更换梁段的设计是影响结构性能的重要因素。
文献研究表明,可更换梁的长度和加劲肋的布置是影响其抗震性能的主要因素。当长度较短时可更换梁发生剪切破坏;而当长度增大到一定范围后,可更换梁发生弯剪破坏。此外,合理布置加劲肋能有效防止可更换梁腹板的屈曲,有助于提高可更换梁的抗震性能,国内外规范[9-10]均对加劲肋的设置做了详细规定。基于此,针对本课题组[11]前期所提带可更换构件的钢筋混凝土柱-钢梁组合框架结构(composite frame consisting of reinforced concrete column and steel beam,RCS)为提高体系中可更换连梁的抗震性能,本文采用ABAQUS有限元软件分析了长度系数对可更换梁的破坏过程、破坏模式、滞回性能、耗能能力、抗剪承载力及变形能力的影响,并基于剪切型可更换梁,分析了加劲肋间距对其破坏过程及抗震性能的影响,进而提出了可更换梁的设计方法和建议,并对其进行试验验证。
1 带可更换构件的RCS混合框架结构
钢筋混凝土柱-钢梁组合框架结构是一种能充分利用和发挥钢和钢筋混凝土构件各自优点的结构形式。而带可更换构件的RCS混合框架结构,是在原组合框架结构抗侧力单元的局部设置一跨度较小的耗能钢框架,如图1所示。该耗能框架由双钢柱及可更换钢梁组成,受力过程中承受竖向荷载并提供大部分抗侧刚度,并由其中的可更换钢梁产生塑性变形集中耗散地震能量。可更换钢梁作为耗散地震能量的关键构件,可设置在楼面层处,也可在每层中间层与楼面层均设置。在地震作用下,可更换梁先于其他构件进入塑性阶段或发生变形,保证主要构件不发生破坏,达到震后可更换的目标,是抗震的第一道防线;RCS主框架单元由混凝土柱、钢梁及共用钢柱组成,主要承受竖向荷载,同时也具有一定的抗侧能力,是抗震的第二道防线。
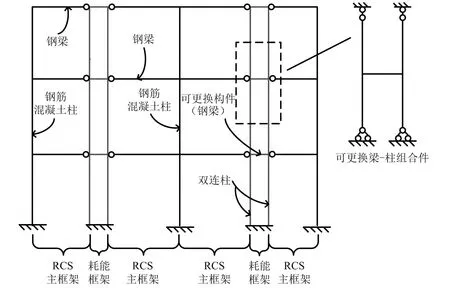
图1 带可更换构件的RCS混合框架结构
2 混合框架可更换梁的试件设计
2.1 试件设计
从某典型RCS混合框架结构的耗能框架中,取可更换梁-柱组合件作为典型计算单元来研究可更换梁的抗震性能(见图1)。可更换梁腹板及端板采用Q235钢,翼缘及钢柱采用Q345钢。可更换梁截面H400×200×10×18,钢柱截面H600×400×14×25,可更换梁与钢柱采用端板-螺栓连接,可更换梁段的构造图如图2所示。可更换梁均设置为单面加劲肋,加劲肋取腹板高度364 mm,厚度取10 mm,端板厚度30 mm。

图2 可更换梁构造图(mm)
2.2 试件参数
本文选择可更换梁的长度系数和加劲肋间距作为研究参数。长度系数为e=l/(Mp/Vp),其中:l为可更换梁长度;Mp为可更换梁全截面屈服弯矩;Vp为可更换梁全截面屈服剪力。本研究设计了两组共18个试件,各试件的参数如表1所示。第一类14个试件,长度系数按照0.1的增量进行设计;为了细化研究长度系数接近1.6时的破坏模式,对长度系数为1.4~1.6的试件以0.05增量进行递增设计。第二类试件是以试件RL4为基础设计的4个不同加劲肋间距的可更换梁试件,分别考虑加密加劲肋及放宽加劲肋间距对可更换梁抗震性能的影响。
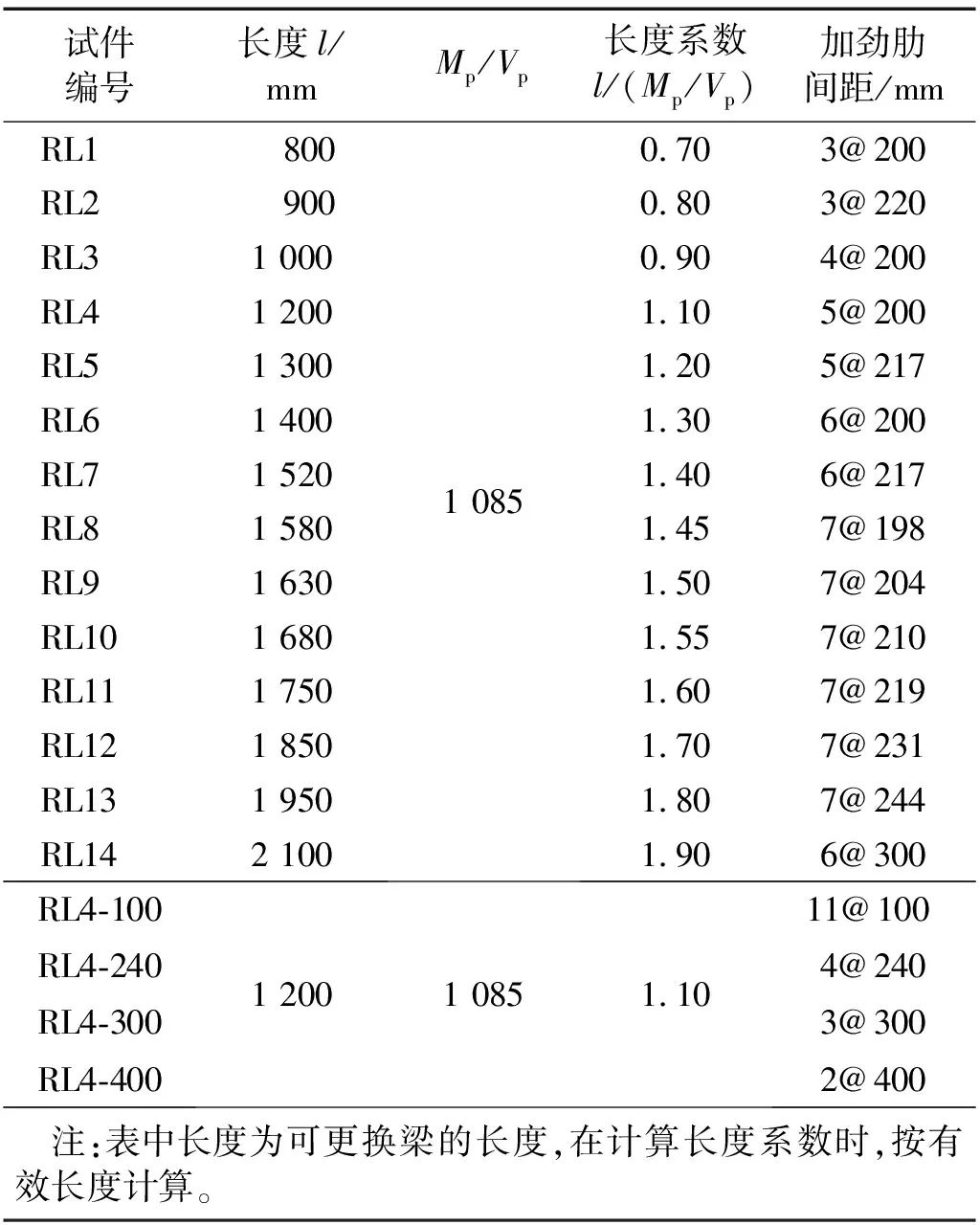
表1 试件参数表
3 有限元模型的建立与验证
3.1 有限元建模
3.1.1 材料的本构关系
模型中,采用Von Mises屈服准则和考虑包辛格效应的随动强化模型,钢材的应力-应变关系如图3所示的三折线模型。屈服强度σy,极限强度σu及弹性模量E均参考文献[12]中钢材的参数,具体取值见表2。钢材的弹性模量取值为E=2.06×105N/mm2,泊松比ν=0.3。

图3 钢材应力-应变关系
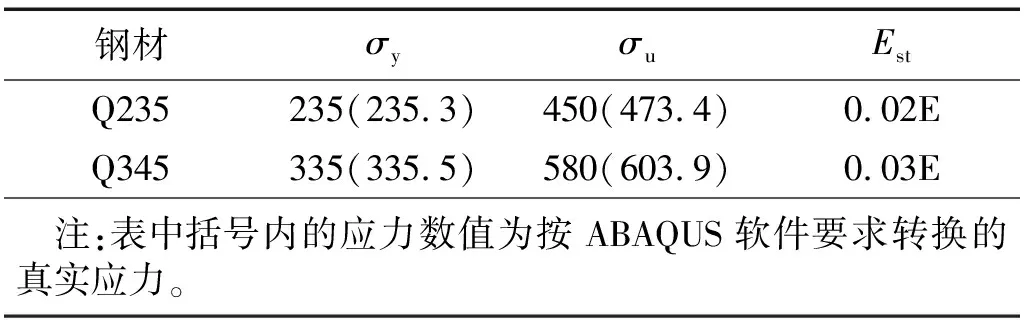
表2 钢材性能参数
3.1.2 接触及边界条件
在建模时,将端板、加劲肋与可更换梁的接触设置为绑定。钢柱翼缘与端板之间设置摩擦接触与螺栓连接接触,面面之间的相互作用通过软件中的切向、法向接触设置进行模拟,钢柱翼缘与端板接触面切向采用“罚”函数定义,摩擦因数取0.45,法向采用“硬”接触定义,由于不考虑螺栓滑移的影响,故螺栓连接采用点面耦合的方式[13]。在有限元建模时,柱顶和柱底都采用铰接约束,在两个柱顶分别建立参考点并在其上同时施加水平往复荷载。
3.1.3 单元类型及网格划分
可更换梁-柱组合件模型如图4所示。其各构件均选用8节点线性减缩积分单元(C3D8R)。为避免线性减缩积分单元可能出现的“沙漏问题”,分析时启用沙漏控制,可更换梁的网格尺寸为30 mm,柱的网格尺寸为50 mm,且沿构件翼缘厚度方向划分四层网格。
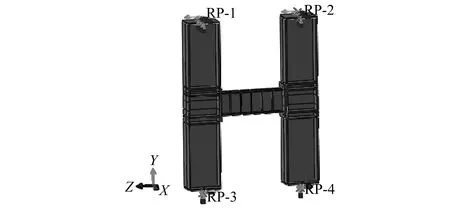
图4 可更换梁-柱组合件模型
3.1.4 加载制度
参考AISC341-10规定的偏心支撑钢框架耗能梁段的加载制度,即采用低周反复荷载,加载由位移控制,如图5所示。
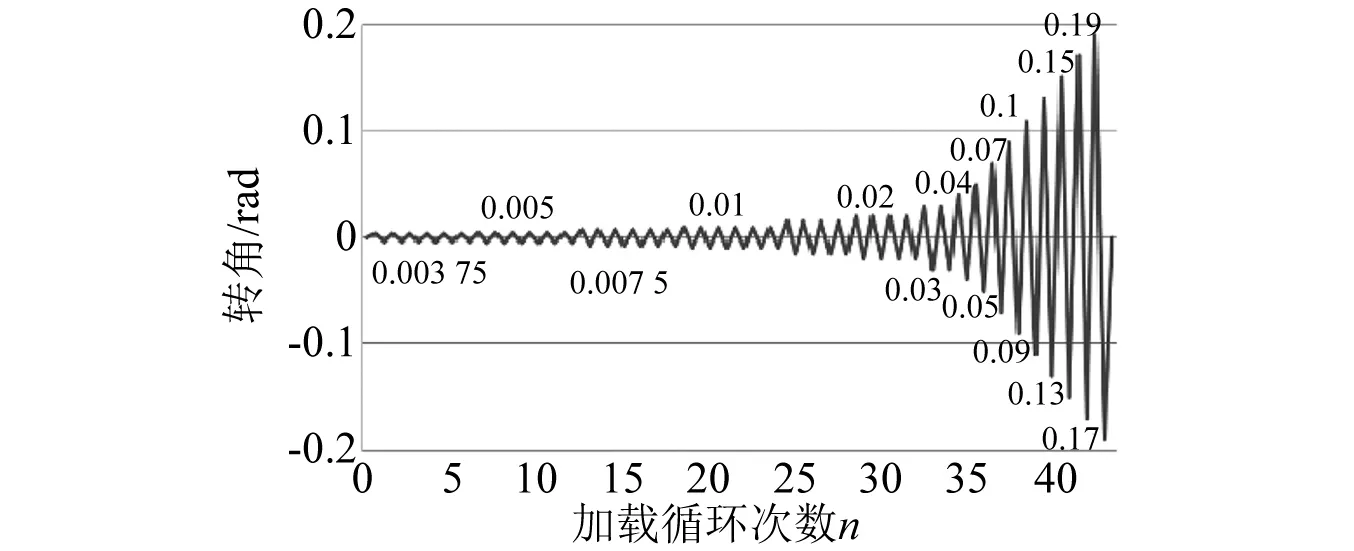
图5 加载制度
3.2 有限元模型的验证
3.2.1 试验简介
本文分别选取文献[14]中的剪切型试件S2和弯曲型试件L1,按3.1节所述方法建立有限元模型,钢材材性、边界条件和加载方式均取自于试验。
3.2.2 破坏特征对比
从梁-柱组合件模型中提取梁段破坏时的有限元应力云图,与试验破坏特征图对比,如图6所示。对比图6(a)、图6(b)可知,试件S2破坏时在有限元中梁腹板达到极限强度,翼缘最大应力区域出现在梁翼缘与端板焊接部分一定距离处,加劲肋最大应力区域出现在与翼缘连接处,端板加劲肋处区域应力较小,整体产生剪切变形。试验中,试件S2右侧翼缘与加劲肋连接处的焊缝发生断裂,腹板形成斜向剪切带进一步引起撕裂,整体也产生剪切变形。由图6(c)可知,试件L1破坏时,有限元中应力最大区域为端板加劲肋旁边的区域,且此区域腹板产生严重屈曲,翼缘有局部失稳,其他区域腹板与翼缘的应力均较小,未发生变形,试件L1为弯曲破坏。该现象与试验中试件L1破坏时端板加劲肋左侧的区域腹板产生屈曲并撕裂、翼缘局部屈曲的现象一致。因此有限元模型较好地反映了两个试件的真实受力。

图6 有限元与试验破坏特征对比
3.3.3 滞回曲线对比
试件S2、L1模拟与试验的剪力-塑性转角滞回曲线,如图7所示。两试件有限元模拟与试验的滞回曲线吻合较好,试件S2呈饱满的菱形,而试件L1呈梭形。且两个试件有限元得到的极限承载力Vmax与试验得到的V′max均较为接近,误差较小。综上,说明可运用上述有限元建模分析方法对混合框架可更换梁进行分析。
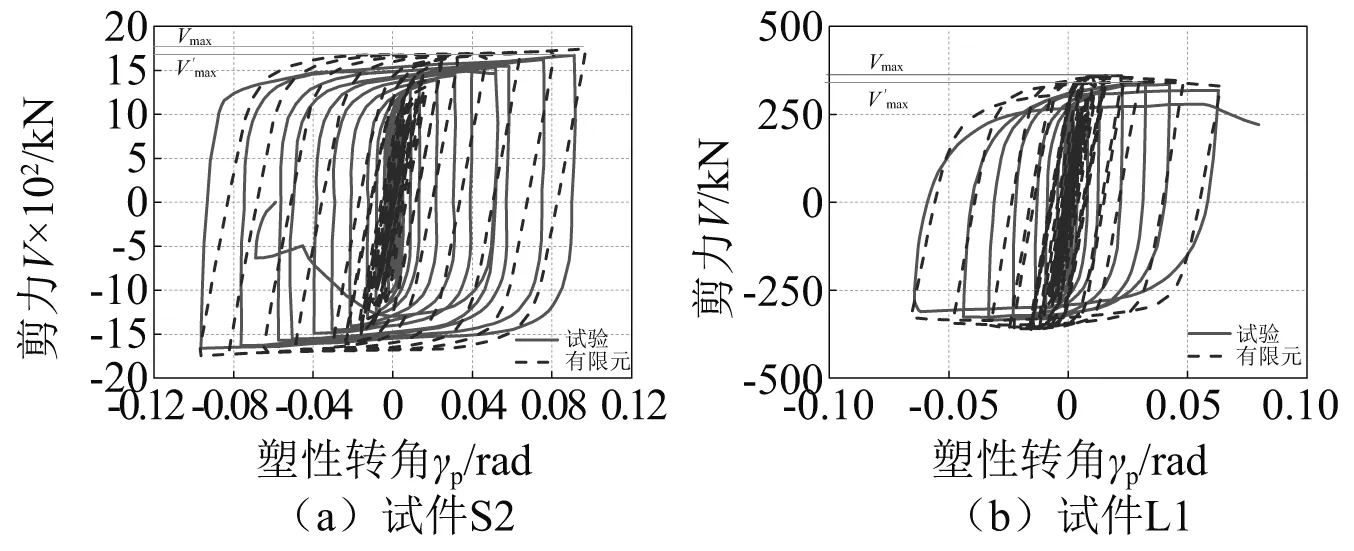
图7 有限元与试验剪力-塑性转角滞回曲线对比
4 长度系数对可更换梁的影响分析
4.1 破坏过程分析
由破坏过程的不同,可将试件RL1~RL14分为两类五组。每类以一个试件为例,可更换梁段达到各受力状态时的应力云图,如图8和图9所示。

图9 试件RL13各受力状态应力云图
第一类试件长度系数e≤1.45,可分为三组。其破坏过程相似,均是腹板首先进入屈服状态,然后逐渐扩展,最终腹板全部达到极限强度并屈曲,试件破坏,而可更换梁-柱节点区域及钢柱应力较小(见图8)。不同的是,第Ⅰ组(RL1、RL2)与第Ⅱ组(RL3、RL4、RL5)试件腹板开始进入屈服状态时所对应的层间位移角相同,而第Ⅲ组(RL6、RL7、RL8)试件较晚;之后,三组试件分别在位移角达到0.05 rad,0.07 rad,0.09 rad时腹板整体达到极限强度;最终分别在位移角达到0.11 rad,0.11 rad,0.13 rad时腹板产生屈曲。

图8 试件RL2各受力状态应力云图
而第二类试件可分为两组,长度系数e>1.45。两组试件破坏过程相似,腹板两端首先开始屈服,然后逐渐向腹板中间扩展,最终腹板两端与翼缘两端均产生屈曲,试件破坏,而组合件节点域在破坏时有部分区域进入塑性状态。不同的是,由于第Ⅴ组(RL13、RL14)试件的长度系数较第Ⅳ(RL9、RL10、RL11、RL12)组试件更大,所以其腹板进入屈服状态更晚;而两组试件均在0.05 rad时腹板两端达到极限强度;在0.09 rad时腹板两端产生屈曲,且翼缘两端也产生局部屈曲。
文献[15]表明,剪切型耗能梁段破坏时梁腹板屈曲并撕裂,弯剪型耗能梁段破坏时腹板两端屈曲,且翼缘也发生局部屈曲现象。因此可判断第一类试件为剪切屈服型;第二类试件为弯剪屈服型,则本文剪切屈服型可更换梁长度系数e≤1.45,弯剪屈服型可更换梁长度系数e>1.45。
4.2 滞回性能及耗能能力
4.2.1 滞回性能分析
剪切屈服型和弯剪屈服型试件的剪力-塑性转角滞回曲线如图10所示。由图10可知,两类试件的滞回曲线都很饱满,具有良好的耗能能力,不同的是剪切型试件的滞回曲线呈菱形,弯剪型试件的滞回曲线呈梭形;随着长度系数的增大,剪切型试件在达到屈服后剪力增长幅度减小,而弯剪型试件在后期会由于翼缘屈曲导致承载力下降。
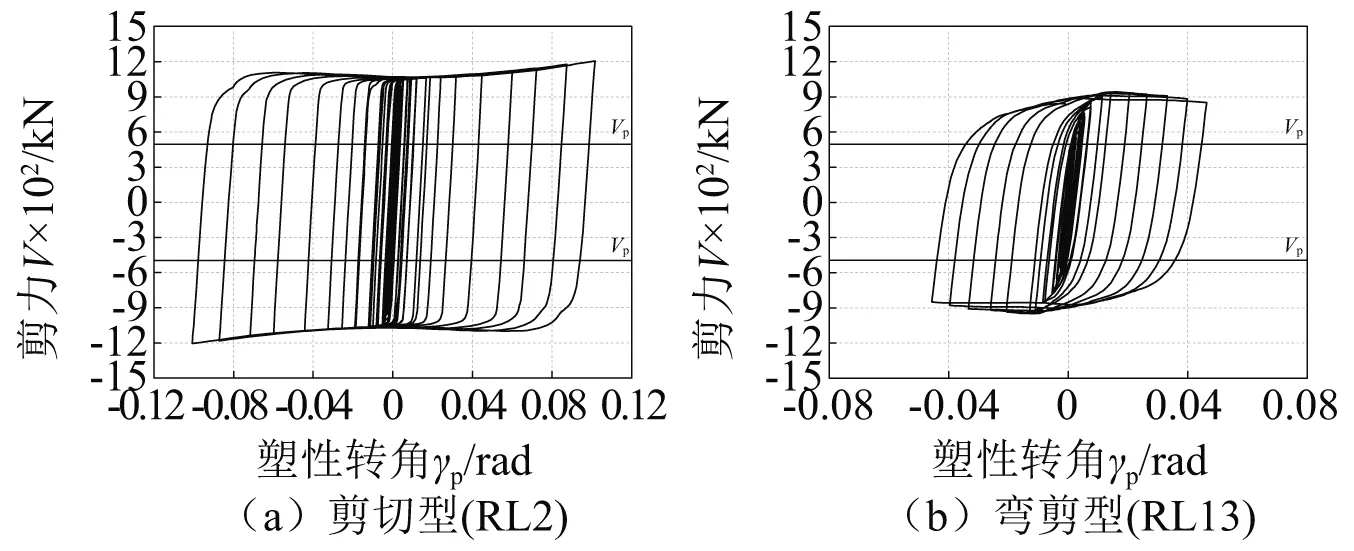
图10 试件剪力-塑性转角滞回曲线
4.2.2 耗能能力分析
由试件滞回曲线可得等效黏滞阻尼系数heq[16],heq越大其耗能能力越强。RL1~RL14试件的累计等效黏滞阻尼系数,如图11所示。随着长度系数的增大,可更换梁耗能能力在逐渐降低。剪切型可换梁耗能变化幅度较大,试件RL1与RL8的累计等效黏滞阻尼系数相差88.11%,而弯剪型可更换梁的耗能变化平缓,试件RL9与RL14的累计等效黏滞阻尼系数仅相差14.62%。

图11 各试件累计等效黏滞阻尼系数
4.3 抗剪承载力及超强系数
为实现可更换梁震后可更换的预期性能目标,要求在可更换梁屈服并强化之后主框架中构件及耗能框架中钢柱等并不完全进入塑性。因此在RCS混合框架结构设计时需考虑可更换梁承载力强化的影响,可用超强系数Ω反映。超强系数Ω为极限抗剪承载力与名义屈服剪力之比,计算公式见式(1)和式(2)。
Ω=Vmax/Vn
(1)
Vn=min{Vp, 2Mp/l}
(2)
式中:Vmax为可更换梁的极限抗剪承载力;Vp为可更换梁的实际屈服剪力,Vp=0.58fyAw,其中fy为钢材实际屈服强度,Aw为可更换梁腹板实际截面积。
国内外114个耗能梁段长度系数与超强系数关系的数据,如图12所示。从图12可知,梁段超强系数随着长度系数的增大而减小,且在长度系数大于1时,梁段的超强系数基本小于AISC341-10提出的超强系数建议值1.5。而本文的可更换梁超强系数均超过了1.5,综合其原因:①由于在实际加载中可更换梁翼缘与端板焊缝易发生断裂,而有限元中条件较为理想,计算的极限抗剪承载力比实际承载力大;②在往复荷载下,影响可更换梁超强系数的因素除了长度系数之外还有其他因素,如由于翼缘和腹板面积比较大而导致翼缘对抗剪有所贡献、腹板钢材强化等因素。
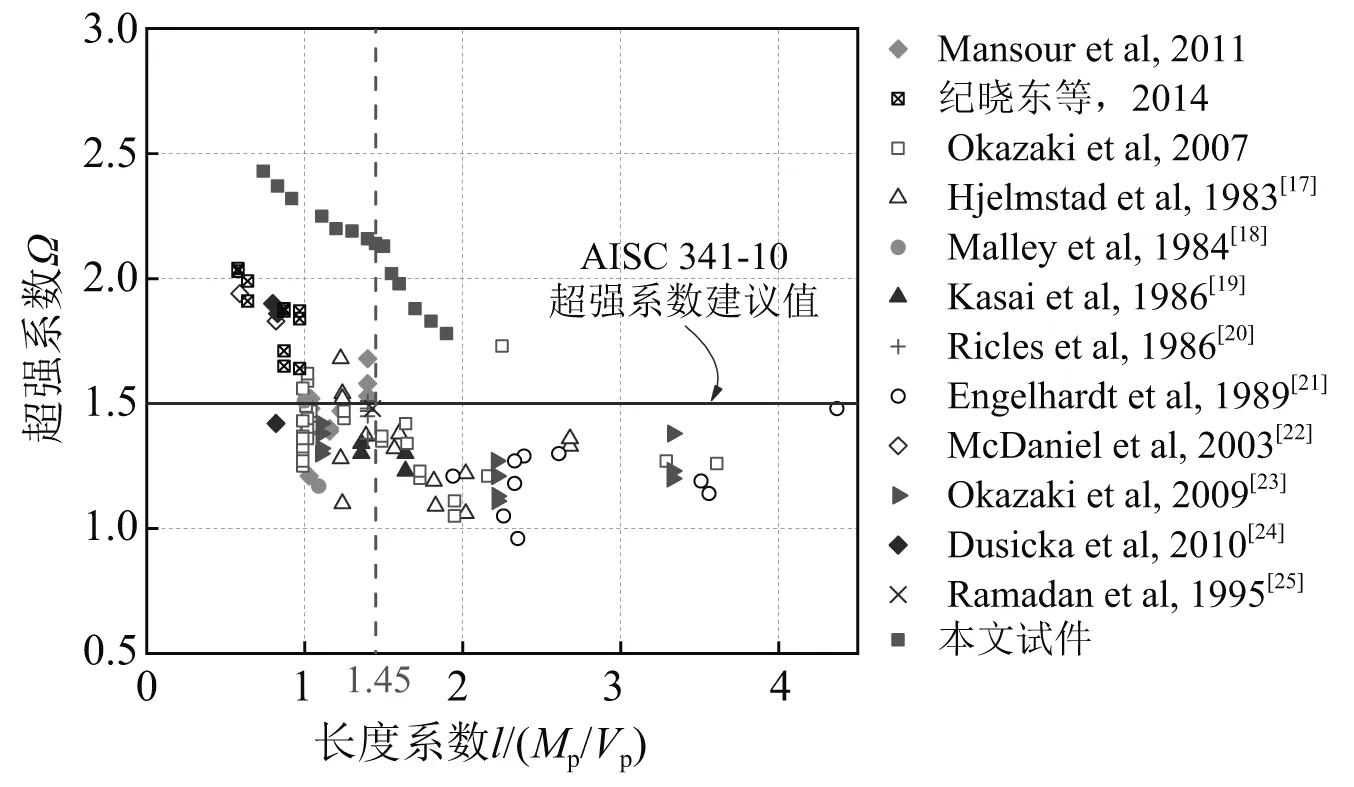
图12 耗能梁段超强系数-长度系数关系
试件RL1~RL14的翼缘剪力Vf及抗剪贡献,如表3所示,其中翼缘抗剪贡献为翼缘剪力Vf与屈服剪力Vp的比值。由表3可知,翼缘抗剪贡献随长度系数增大而减小,剪切型可更换梁的翼缘抗剪贡献平均值为29.81%,弯剪型可更换梁的翼缘抗剪贡献平均值为13.72%,两者均较高,不可忽略;随着长度系数增大,试件的弹性刚度与极限剪力均减小,试件RL1的极限抗剪承载力最大,试件RL14最小,两者相差37.58%,因此长度系数对可更换梁抗剪承载力影响较大。超强系数随长度系数增大而减小,最大达到2.43,最小为1.78。剪切型可更换梁的超强系数平均值为2.26,弯剪型可更换梁的超强系数平均值为1.94。
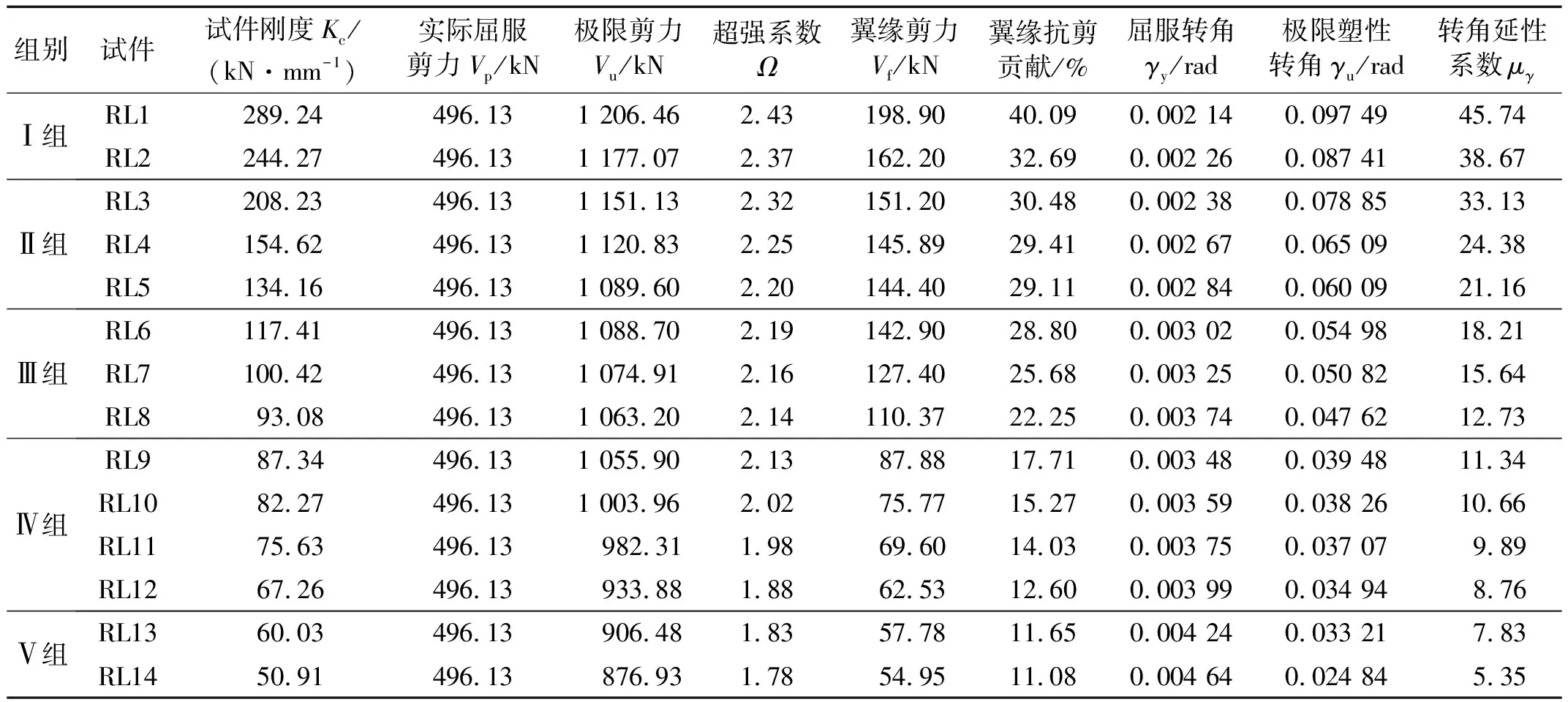
表3 试件的抗剪承载力与变形能力
可更换梁的超强系数必须采用合理的取值,若取值太小,非耗能构件设计偏于不安全,若取值太大,使其他构件设计偏于保守而不经济。故建议剪切型可更换梁的超强系数Ω取2.26,弯剪型可更换梁的超强系数Ω取1.94。
4.4 变形能力
表3列出了各试件的屈服转角γy、极限塑性转角γu和转角延性系数μγ。试件的屈服转角γy由屈服剪力Vp除以弹性刚度Kc得到,而弹性刚度Kc参考纪晓东等试验研究公式。构件的极限塑性转角γu由破坏时的转角减去屈服转角得到。延性是反应构件抗震性能的一项重要指标,构件延性越好,说明其耗能能力与变形能力越强。本文采用转角延性系数μγ来分析各试件的延性,由极限塑性转角除以屈服转角得到。随着可更换梁长度系数增大,极限塑性转角与转角延性系数均减小(见表3)。
试件RL1~RL8属于剪切型可更换梁。第Ⅰ组试件(e<0.9)的转角延性系数平均值达到了42.21,极限塑性转角平均值为0.092 5 rad,超过AISC规范对剪切型耗能梁段塑性转角的限值0.08 rad,说明其塑性转动能力很好;虽然试件RL3~RL8的塑性转动能力小于0.08 rad,但满足实际工程中对塑性转角不低于0.03 rad的要求。试件RL9~RL13属于弯剪型可更换梁,极限塑性转角均超过实际工程要求0.03 rad。试件RL14的极限塑性转角为0.024 8 rad,小于0.03 rad,不满足工程要求。
当长度系数过小时,虽然可更换梁的变形能力很好,但其腹板达到各受力状态较早,且其极限抗剪承载力与超强系数过大,对框架不利,不建议长度系数取值过小;当长度系数在1.3~1.45时,可更换梁的塑性转动能力降低,耗能能力减小;而当长度系数在0.9~1.2时,其塑性转动能力及耗能能力均较好。故建议将可更换梁的长度系数设计在0.9~1.2。
5 加劲肋间距对可更换梁的影响分析
5.1 破坏过程分析
RL4系列试件受力状态发展对应的层间位移角,如表4所示。各试件均在0.007 5 rad时可更换梁腹板全部屈服,试件RL4(RL4-200)与RL4-240均在0.11 rad时腹板出现屈曲;试件RL4-300和RL4-400分别在0.09 rad,0.02 rad时腹板产生屈曲;试件RL4-100加载至最后腹板未出现屈曲,说明加劲肋加密后有效防止了可更换梁腹板的屈曲,而加劲肋间距较大的试件腹板更早产生屈曲,且间距越大,腹板屈曲越早。
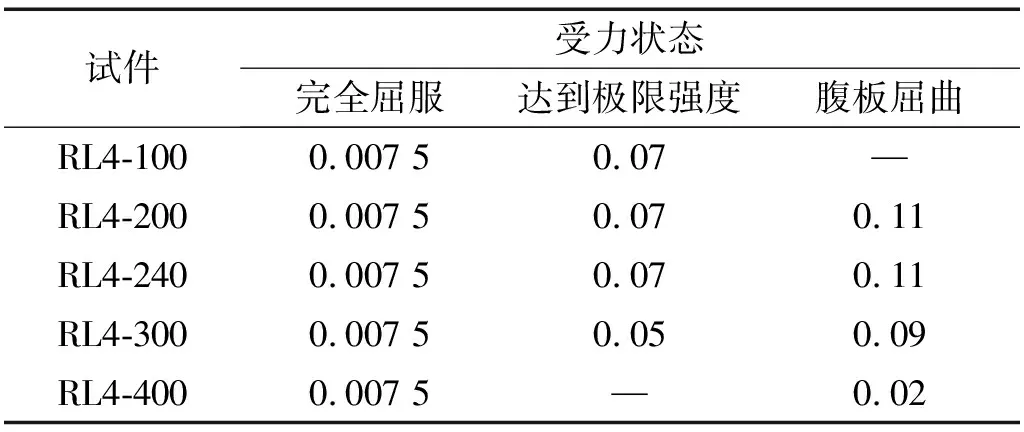
表4 试件受力状态发展
5.2 滞回性能及耗能能力
5.2.1 滞回性能分析
不同加劲肋间距试件的剪力-塑性转角滞回曲线,如图13所示。从图13可知,试件RL4-100、RL4、RL4-240与RL4-300的滞回曲线均呈很饱满的菱形,而试件RL4-400由于腹板过早屈曲导致其滞回曲线在加载后期饱满性降低;各试件在加载前期,滞回曲线均呈线性,进入塑性后,加劲肋间距按照规范设置的试件RL4抗剪承载力略有增大,而加劲肋间距增大的试件抗剪承载力基本不增长;各试件的塑性转角差别较大,加劲肋间距增大的试件由于腹板屈曲较早,其塑性转角较小。
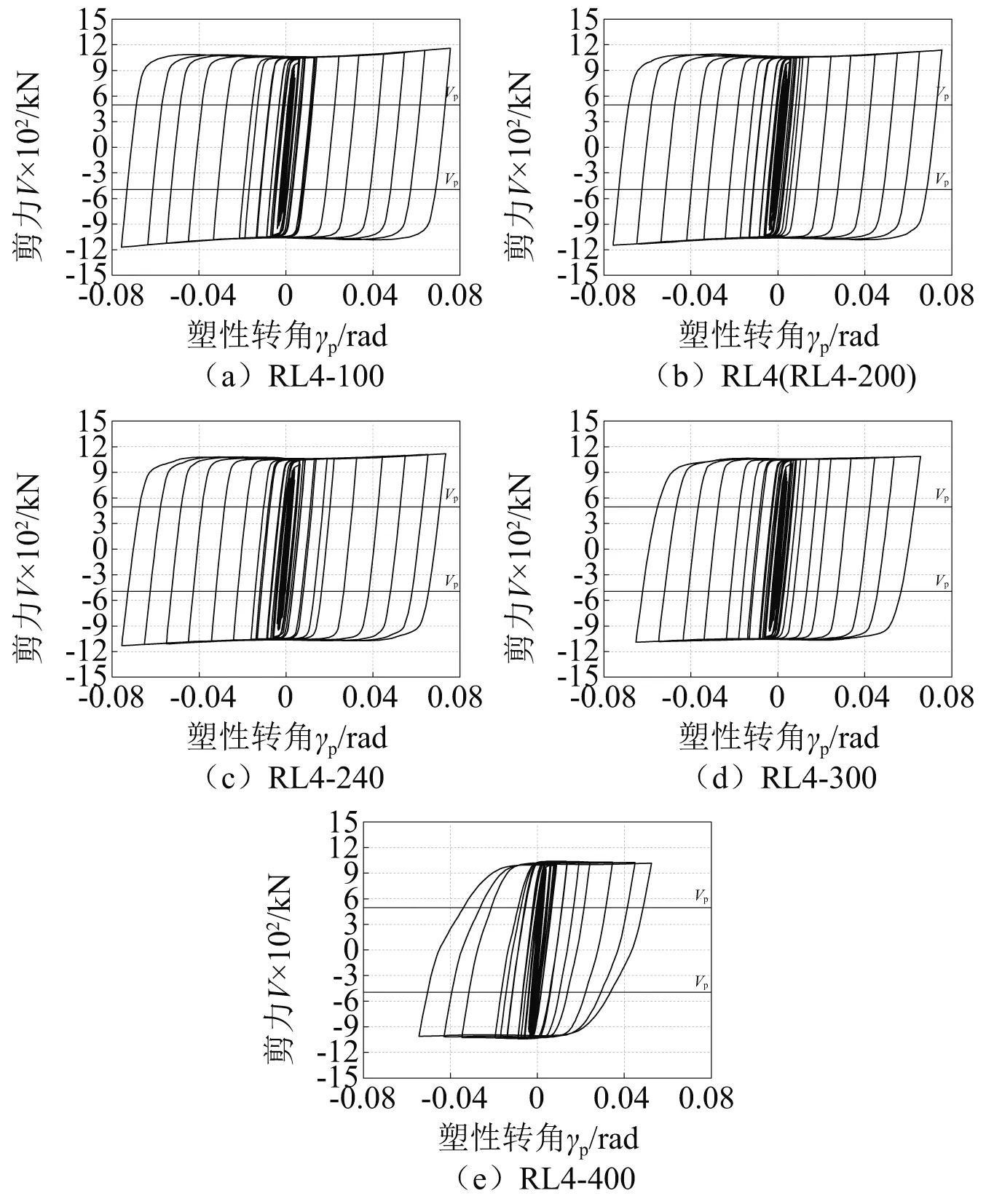
图13 剪力-塑性转角滞回曲线
5.2.2 耗能能力分析
不同加劲肋间距试件的累计等效黏滞阻尼系数,如图14所示。由图14可知,加密加劲肋对可更换梁的耗能能力有所提高;随着加劲肋间距的增大,可更换梁试件的耗能能力降低。当加劲肋间距不满足规范要求且超出规范限值较多时其耗能能力大大下降,而加劲肋间距设置略超过规范时(RL4-240)其耗能下降很少。
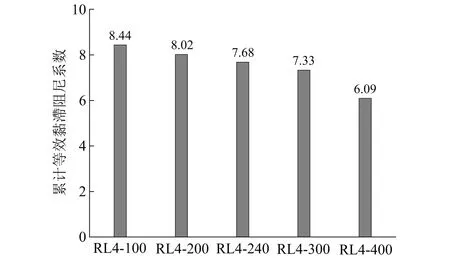
图14 耗能能力对比
5.3 抗剪承载力及变形能力
5.3.1 抗剪承载力
不同加劲肋间距试件的极限抗剪承载力及塑性变形,如图15所示。从图15可知,随着加劲肋间距增大,试件极限抗剪承载力逐渐减小,RL4-100试件比RL4-400试件极限承载力高了9.68%,说明加劲肋间距对抗剪承载力影响较小。

图15 不同加劲肋间距极限剪力及极限塑性转角变化规律
5.3.2 变形能力
随着加劲肋间距的增大,各试件的极限塑性转角减小(见图15)。加密加劲肋间距对可更换梁的塑性转动能力有所提高;加劲肋间距略超过规范要求值时塑性转动能力降低幅度不大,但加劲肋间距增大较大时,其塑性转动能力大大降低。
加密加劲肋能有效防止可更换梁腹板屈曲,并提高其抗剪承载力与变形能力;加劲肋间距超过规范要求且间距增大较大时,会使可更换梁腹板过早屈曲,并使其耗能能力与塑性转角显著降低。故不建议将剪切型可更换梁的加劲肋间距设置过大。
6 可更换梁的设计方法及算例验证
6.1 可更换梁的设计方法
6.1.1 长度系数及截面尺寸
为保证可更换梁在地震作用下有良好的塑性变形能力及耗能能力,建议在设计可更换梁时应将其设计成剪切屈服型。首先根据其剪力设计值算得腹板面积,初步确定可更换梁截面尺寸,再根据结构要求及抗震验算[26]对截面进行调整,最终确定截面尺寸。
再根据截面尺寸确定Mp/Vp的比值,最终确定试件的长度系数,按照式(3)、式(4)计算
e=l/(Mp/Vp)
(3)
Mp=fyWp
(4)
式中:e为可更换梁的长度系数,取值范围建议为0.9~1.2;Wp为塑性截面模量。
6.1.2 承载力设计
可更换梁的屈服剪力参考:GB 50011—2010《建筑抗震设计规范》中耗能梁屈服剪力公式,即
Vp=0.58fyAw
(5)
由前文可知,长度系数e增大,极限抗剪承载力与超强系数均减小。剪切型和弯剪型可更换梁的超强系数Ω平均值分别为2.26和1.94,因此可更换梁的极限承载力按式(6)计算
(6)
此外,在进行框架梁设计时,为保证在可更换梁进入塑性且充分发展时框架梁处于弹性状态,应使其承载力大于可更换梁的极限承载力。
6.1.3 构造措施
可更换梁的构造措施包括翼缘宽厚比、腹板高厚比及加劲肋设置。为避免可更换梁过早出现局部屈曲而影响其耗能能力及变形能力,可更换梁翼缘宽厚比及腹板高厚比限值参考规范中对偏心支撑框架耗能梁段的规定。
为避免可更换梁腹板过早发生剪切屈曲而影响其耗能能力,可更换梁应设置竖向加劲肋。剪切型可更换梁加劲肋应按以下要求进行布置:
可更换梁截面高度不大于640 mm时,可配置单侧加劲肋,截面高度大于640 mm时,应在两侧配置加劲肋;加劲肋宽度不应小于(bf/2-tw),厚度不应小于max{0.75tw,10};加劲肋间距应按规范要求设置,不大于(30tw-h/5)。
6.1.4 可更换梁与耗能框架钢柱连接设计
可更换梁与耗能框架钢柱直接连接,在连接设计时应保证节点连接的承载力高于式(6)中可更换梁的极限承载力,同时保证耗能框架钢柱的刚度高于可更换梁的刚度,从而确保可更换梁集中耗能,且破坏发生在可更换梁上。再根据规范要求计算螺栓受力,确定螺栓布置形式、数量及间距等。同时使可更换梁便于更换。
6.2 算例验证
6.2.1 试件设计
基于上述可更换梁设计方法,设计三个端板-螺栓连接的剪切型可更换梁试件,并通过试验验证所提设计方法的有效性。主要步骤如下:
已知在地震作用下,可更换耗能梁的弯矩、轴力和剪力设计值分别为450 kN·m,400 kN和500 kN。
步骤1试件长度选择常用的0.8 m,1.0 m和1.2 m,各试件对应编号为RB2、RB3和RB4;试件腹板及端板采用Q235钢,翼缘采用Q345钢。
步骤2剪切型可更换梁按照腹板受剪的强度条件进行设计,即剪力设计值V<0.9Vp/γRE,其中γRE为耗能梁承载力抗震调整系数,取0.75。可得试件腹板面积(Aw)min=2 751 mm2,各试件可选相同截面尺寸,初选截面尺寸为H400×200×10×18。
步骤3对初选截面进行验算——按照腹板受剪、翼缘受轴力和弯矩的强度条件进行。
因N=400 kN<0.15Af=435.99 kN,则
腹板强度条件
0.9Vp/γRE=0.9×0.58×235×10-3×10×364/0.75=
595.36 kN>500 kN
翼缘强度条件
If=[(1/12)×200×183+200×18×1912]×2=
264 996 000 mm4
Wf=If/(h/2)=1 324 980 mm3
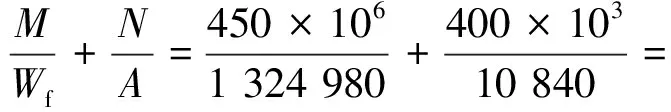
376.53 N/mm2<295/0.75=393.33 N/mm2
满足条件,则试件截面尺寸定为H400×200×10×18。
步骤4由试件截面尺寸,确定Mp/Vp的比值为1 085,再按式(3)得各试件长度系数分别为0.9,1.1和1.1,满足剪切型耗能梁的长度系数范围e≤1.45,试件设计有效。
步骤5按构造要求,各试件设置竖向加劲肋,加劲肋取腹板高度364 mm,厚度取10 mm,具体布置方式如表5所示。试件翼缘宽厚比为11.1<16,腹板高厚比为36.4<69.5,满足规范要求。
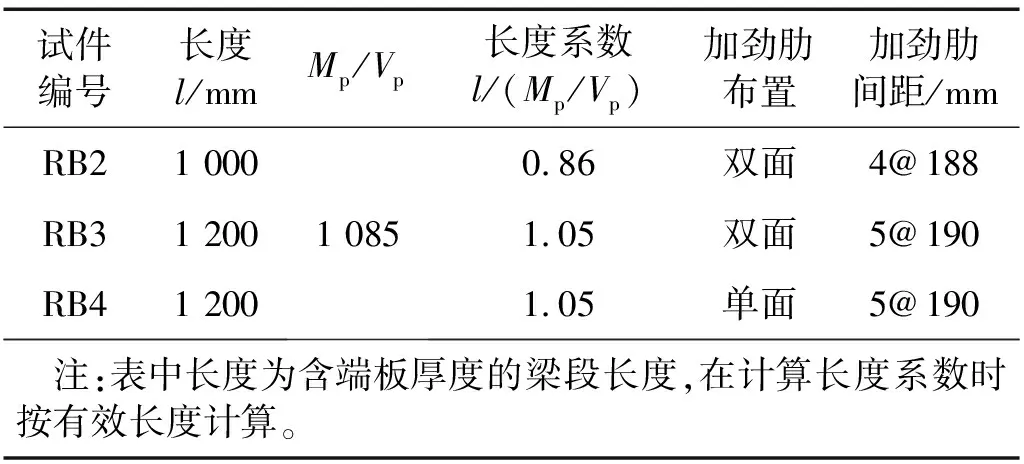
表5 试件参数
步骤6钢柱截面规格为H600×400×14×25,各试件与钢柱均采用端板-螺栓连接,端板厚度30 mm。端板采用Q235钢,钢柱采用Q345钢,钢柱翼缘与端板接触面采用喷砂处理。试件照片如图16所示。

图16 试件照片
步骤7试验加载装置如图17所示。加载制度见图5,采用位移加载控制。

图17 加载装置
6.2.2 设计方法验证
(1)滞回性能
试件剪力-塑性转角滞回曲线,如图18所示。从图18可知,各试件的滞回曲线呈饱满的菱形,具有优异的耗能能力和变形能力,与前文模拟结果一致。不同的是各试件均出现了轻微滑移现象,这是试验装置限制所致。各试件在加载前期,滞回曲线均呈线性,进入塑性后,抗剪承载力略有增大。
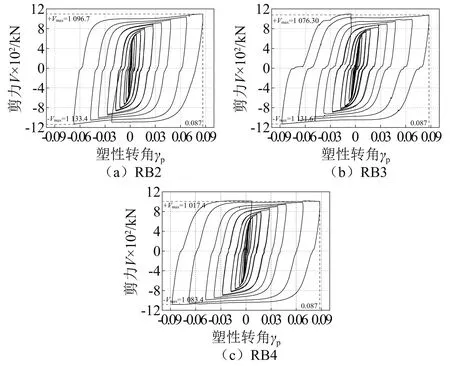
图18 剪力-塑性转角滞回曲线
(2)耗能能力
各试件的累计等效黏滞阻尼系数,如表6所示。试件RB2的累计等效黏滞阻尼系数大于RB3,与前文模拟一致,长度系数越大,耗能能力越低;在长度系数相同时,试件RB3的累计等效黏滞阻尼系数大于RB4,说明采用双面加劲肋布置的可更换梁耗能能力大于采用单面加劲肋布置的可更换梁,但耗能下降很少。
(3)抗剪承载力
试件RB2、RB3和RB4的长度系数均小于1.45,则超强系数取2.26,再按式(6)算出各试件的抗剪承载力计算值为1 121.26 kN。抗剪承载力计算值与试验值的误差分析见表6,可以看到各试件的抗剪承载力试验值与计算值均在10%以内,误差较小,说明本文所提可更换梁的承载力公式合理。
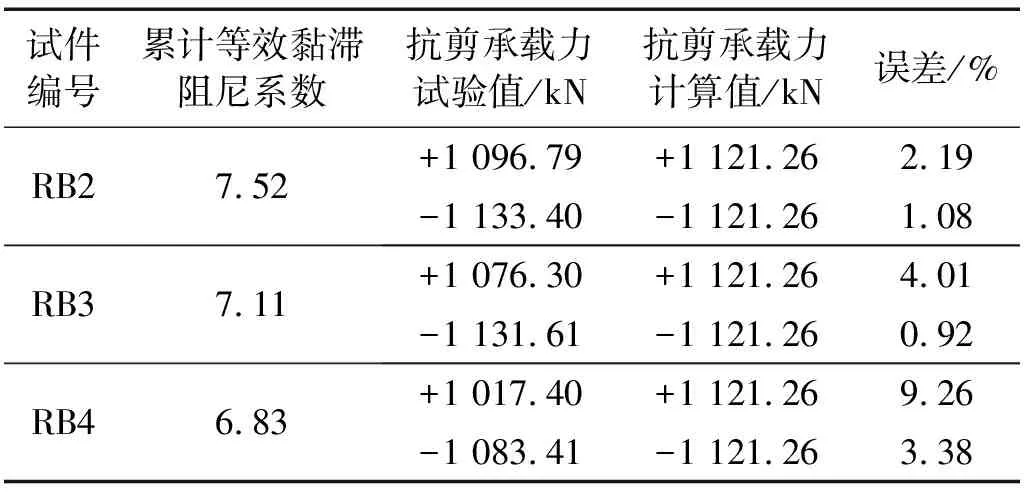
表6 试件耗能能力与抗剪承载力
(4)变形能力
各试件的极限塑性转角均可达到0.087 rad,满足AISC 341-10对于消能梁段极限塑性转角0.08 rad的限值要求,说明按照所提方法设计的试件,塑性转动能力足够,梁具有良好的可更换性。
7 结 论
(1)长度系数对混合框架可更换梁的破坏过程、破坏模式影响显著,本文提出剪切屈服型可更换梁的控制参数为1.45,即当长度系数e≤1.45时,可更换梁为剪切屈服型梁。
(2)可更换梁的耗能能力、抗剪承载力及超强系数随着长度系数的增大而减小;试件的超强系数平均值均超过AISC提出的超强系数建议值;长度系数越小,塑性转动能力越大。故建议可更换梁的长度系数设计范围为0.9~1.2。
(3)加劲肋间距超过规范要求且间距增大较大时,会使可更换梁腹板过早屈曲,其耗能能力与塑性转角显著降低。因此,建议可更换梁的加劲肋间距按照规范要求进行设置,即对于剪切型可更换梁,加劲肋间距不应大于(30tw-h/5)。
(4)基于各参数分析结果,从可更换梁长度系数、承载力设计、构造措施及可更换梁-柱连接设计等四个方面给出可更换梁的设计方法。
(5)设计并进行了可更换梁的试验验证。试验表明,各试件的耗能能力、抗剪承载力和变形能力较好,具有良好的可更换性,本文所提设计方法合理。

