涡旋电磁波无线通信技术的研究进展

赵林军 张海林 刘乃安

①(陕西理工大学物电学院 汉中 723000)

②(西安电子科技大学通信工程学院 西安 710071)

1 引言

由香农信道容量定理[1]可知，无线通信系统的数据传输速率与该系统的带宽成正比。面对未来超大容量数据传输需要，即使应用了多天线等频谱增强等技术[2,3]，传统的平面电磁波通信技术面临频谱资源枯竭的窘境。在太赫兹的应用中，人们发现该技术也面临着环境风险与其器件的制造等问题[4-6]。在此背景下，人们试图利用电磁波的轨道角动量(Orbital Angular Momentum, OAM)携带信息实现大容量传输。

根据电磁动力学知识[7,8]，电磁波的轨道角动量是其角动量的一部分。研究表明，携带OAM的电磁波的波印廷矢量轨迹是一条围绕其波束方向的螺旋曲线，从而影响其波前呈涡旋状。因此，具有OAM的电磁波的波前场分布具有与其拓扑荷ℓ(俗称模态)相关的特殊“极化纹理”。目前，学界将OAM驱使的电磁波称为涡旋电磁波。

电磁波携带的OAM首先在光学中被发现与应用[9]。直到2007年，文献[10]将其引入无线射频领域。与平面电磁波无线通信技术[11-13]发展相比较，涡旋电磁波通信技术的应用研究时间短[14,15]，尚有其传播机理与MIMO结合等科学或工程问题有待解决。

本文从7个方面总结了有关涡旋电磁波在无线通信领域的研究成果，给出涡旋电磁波传播机理与收发等问题的解决途径或方法，以促使该技术的发展。

本文后续章节的安排如下：第2节论述了电磁场(波)的动量理论；第3节论述了轨道角动量与模态ℓ的逻辑关系；第4节论述了定性分析涡旋电磁波的传播特性；第5节论述了涡旋电磁波在无线射频领域中的应用；第6节涡旋电磁波与 MIMO 的兼容性研究；第7节论述了涡旋电磁波无线通信演示验证；第8节为结论。

2 电磁场(波)的动量理论

2.1 电磁场(波)的动量

采用分离变量方法[16]可由式 (1) 所示的达朗贝尔(d’Alembert)方程[17]，

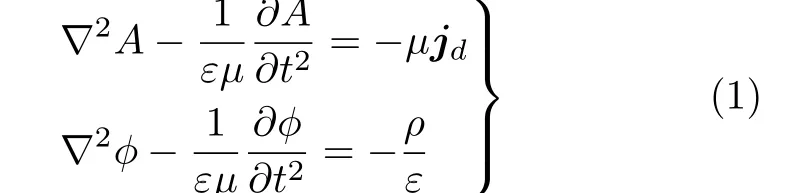
确定电磁波的矢量势A与其标量势ϕ。

由洛伦兹(Lorentz )规范，可确定介质中电磁波的电场强度矢量E与磁场强度矢量H，

式(1)与式(2)中，∇为矢量微分运算子；jd为天线阵子的激励电流密度，ρ为电荷密度；ε为传播介质的电介常数，µ为传播介质的磁介常数。

根据文献[18]，可确定电磁波的动量体密度如式(3)所示，

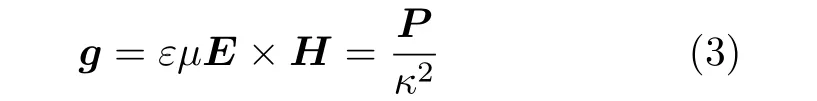
其中，P为电磁波的坡印廷矢量，κ为介质中电磁波的传播速度。可见，均匀介质中，电磁波的动量体密度g与电磁波的坡印廷矢量P是同向的[8,19]。

对式(3)两边关于时间求导数，如式 (4)所示，

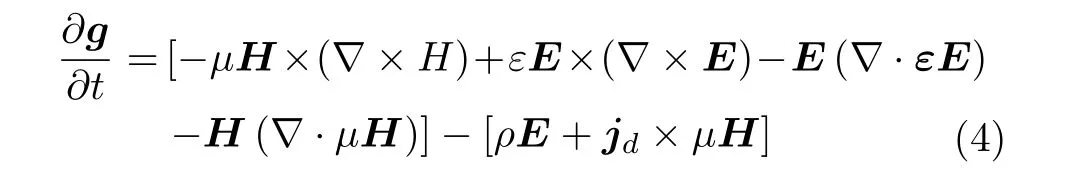
其中，第1个[·]项定义了电磁波的动量密度流，第2个[·]项定义了空间电荷所受电磁力的密度，物理学上将这种作用力称为功率密度[19]。显然，在无带电体空间，式 (4)可简化为

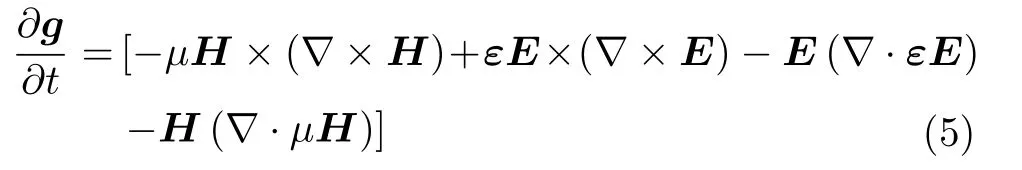
可见，电磁波的动量密度流具有力(密度)的物理属性。

2.2 电磁波的角动量

由文献[20]可知，漩涡状的龙卷风中具有“轴向”运动特性，其中水雾的运动就是其携带的角动量所致。为了便于理解，不妨以图1所示的质点系进一步说明运动物质的角动量的功能。设图1中质点1、质点2与质点3的质量分别为m1,m2与m3，它们各自的运动速度为v1,v2与v3，建立以观测点O为原点的2维坐标系，质点系的质心c有运动速度vc，则该质点系的总角动量[21]为

图1 携带角动量的质点系[21]

其中，L为轨道角动量，S为自旋角动量。

式(6)说明质点(系)的动量是其角动量存在的前提；角动量中的自旋角动量S分量不以观测点O的位置变化而变化，因此S具有內禀性；角动量中的轨道角动量分量还取决于观察点O的位置，即由观察点O确定的径矢rc方向与大小。显然。式(6)中的轨道角动量L不恒为0时，则图1中的质心c相对观察点O有一条运动曲线，换句话说，轨道角动量L决定了质心c的运动轨迹。

现在以图2所示的电基本阵子辐射波为例研究电磁波的角动量的作用。参照图1所述的质心c，图2中电磁波波束的“质轴”可为电磁波波束传播方向(坡印廷矢量P的指向)为轴。

图2中点a有磁场矢量Ha、电场矢量Ea，由式(3)可确定a点的动量密度为ga。若以点c为观测点存在径矢rac，则可确定其角动量体密度[22,23]为

不失一般性，式(7)的径矢rac可记为r,Ha记为H,Ea记为E。在体积V内对式(7)计算体积分，可得体积V内的电磁波携带的总角动量为

显然，平面电磁波远场时, 由于径矢ra与a点的坡印廷矢量Pa同向，因此J≡0，但角动量体密度ga不恒为0。那么，平面电磁波波束的“质轴”是怎样变化的呢？这就需要进一步考察其轨道角动量。

2.3 电磁波的轨道角动量

显然，图2中以c点看a点电磁波，其角动量密度ja不 恒为0。因此，可由文献[9]知a点处的电磁波波束的波前是非平面的。

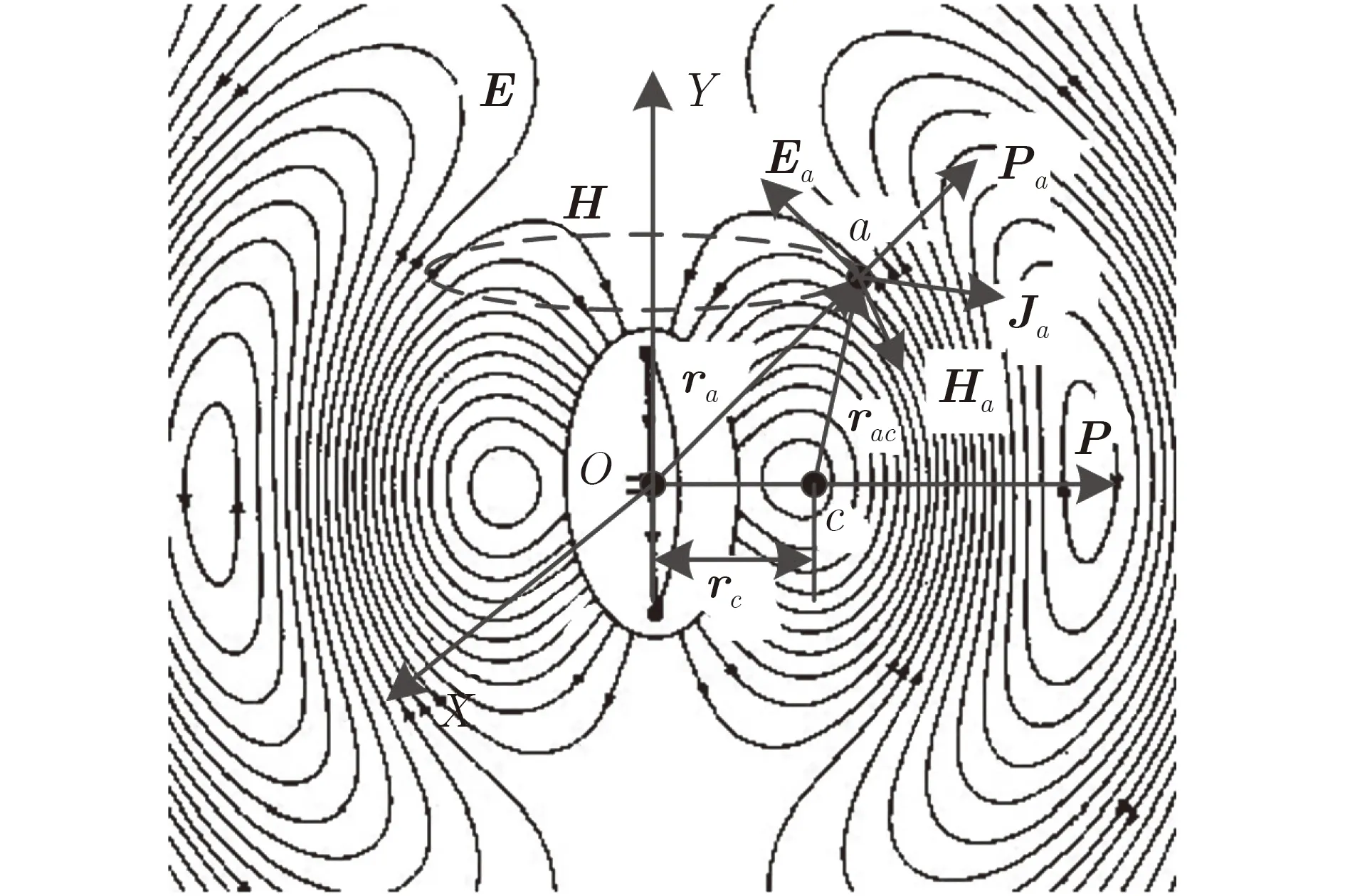
图2 电基本阵子角动量密度矢量示意图[21]

文献[24]认为携带OAM的电磁波的坡印廷矢量P是沿波束方向Z轴呈现螺旋状的，如图3所示。

图3 携有OAM电磁波坡印廷矢量轨迹及其波前结构示意[24]

因此，涡旋电磁波的波前电场矢量分布是围绕其传播轴的旋涡状分布，如图4所示，其中图4(a)说明了涡旋电磁波的波前电场强度矢量E围绕传播方向具有特殊的“极化纹理”分布；图4(b) 又说明涡旋电磁波的波前“极化纹理”是可以沿传播轴向传播的。学界将涡旋电磁波的波前场矢量[9,26]建模为

图4 涡旋电磁波波前电场相位示意图

其中，s˙(t)为复数振幅；ω为载频频率；ℓ为涡旋电磁波的模态，φ是围绕波束传播方向的方位角。

从信号的角度分析式(9)，涡旋波信号的数学模型比普通信号模型多了一个与OAM模态ℓ相关的傅里叶旋转因子 ejℓφ。 显然，因子ejℓφ具有不同模态ℓ关于方位角φ的正交性特性，这就预示了不同模态涡旋电磁波信号具有共享信道传输的能力[25,27]。同时，当ℓ=0时，式(9)退化为普通的平面波信号，这也说明平面电磁波是涡旋电磁波的一个特例。

3 轨道角动量与其模态的关系

柱坐标下，文献[28]对极化矢量势为A=u(x,y,z)ejkz ·ex(ex为x轴的单位向量)，电磁波的动量密度g建模为

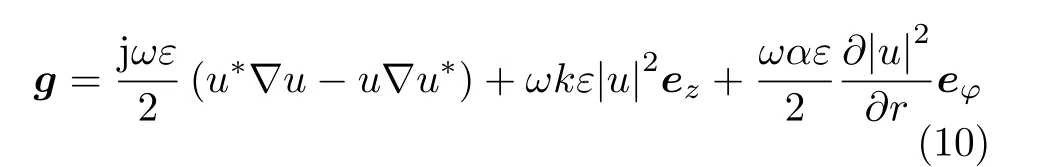
其中，∇为柱坐标系下的矢量微分算子，ω为信号的载频，k为波数，α=+1表 示右旋圆极化，α=−1为左旋圆极化，α=0 为线极化，ez与eφ分别为柱坐标系下Z轴与ϕ轴的单位矢量。

柱坐标下，由径矢r=(r,0,φ)可确定该电磁波的动量体密度gφ对其轨道角动量密度Lz是有贡献的，在柱坐标下，Lz的大小为

其中gφ表 示取式(10)的ϕ轴的分量取值。

对于涡旋电磁波，其电场强度矢量E与磁场强度矢量H均含ejℓφ因子[29]。因此涡旋电磁波的动量体密度g必然含有模态ℓ信息。经推演，在文献[28]基础上，文献[29]对模态为ℓ的涡旋电磁波的轨道角动量密度Lz的大小建模为

其中α=+1表 示右旋，α=−1为左旋。

分析式(12)，有如下结论：

(1) 相同模的矢量势A，不同模态ℓ涡旋电磁波沿其传播轴向z的轨道角动量lz大小不同；

(2) 由矢量的运算规则，波印廷矢量的Pr分量对涡旋电磁波的(轨道)角动量密度Lz是有贡献的。当模态ℓ越大时，可以确定Pr越大，意味着该模态的波束具有较大的开口；

(3) 与波印廷矢量的Pr分量相对应的电场量因可由圆锥金属板可其反射，因此使用一定立体角的圆锥金属板可以以实现对涡旋电磁波波束的汇聚。结合结论(2)，单一的波束汇聚方法难以对模态复用涡旋电磁波波束的实现一致性汇聚。

上述结论可由文献[30,31]间接佐证。

4 涡旋电磁波的传播特性

开放介质中涡旋电磁波的传播也必然存在反射、折射以及散射等现象。目前，无线射频波段关于涡旋电磁波的传播特性的研究成果报道的较少，借助平面电磁波的传播特性[32]，定性分析涡旋电磁波在分层介质与大气湍流中的传播特性，不失为一个捷径。

4.1 涡旋电磁波在分层介质的传播特性

4.2 涡旋电磁波在湍流介质中的传播特性

涡旋电磁波在大气介质中传播时必然存在大气湍流的散射[34]。由于无线射频信号的波长较大，相同尺寸的大气湍流对无线射频信号模态的影响小于对光信号模态的影响[35]。尽管如此，湍流尺寸的变化对不同波长信号的影响[36]，要求涡旋电磁波通信系统必须对波束需进行优化设计[37,38]。目前，关于大气湍流对涡旋电磁波的影响以及涡旋电磁波波束优化设计的研究成果较少。

5 涡旋电磁波在无线射频领域中的应用

学界已经对涡旋电磁波通信信道容量提升[39]能力、用户信息的隔离[40]能力以及基于模态正交接入[41]的组网等进行了初步探索。现主要成果主要集中在涡旋电磁波产生、模态分离以及涡旋电磁波与MIMO的兼容3个方面。

5.1 涡旋电磁波的产生OAM波

5.1.1 波束移相法

在无线射频领域，波束移相法主要是通过调控平面电磁波波束不同区域相位实现涡旋电磁波波束的。理论上，这类涡旋电磁波的波印廷矢量的Pr分量、Pφ分量与Pz分量均存在，因此它属于“立体”的。

基于波束移相的涡旋电磁波的产生方法主要包括：螺旋反射面[42]、螺旋相位板[43]、人工电磁材料反射面[44]、人工电磁材料透镜[45]等方法，如图5所示。从通信角度来看，这类涡旋电磁波的产生方法的缺点主要有：调制信息的加载方式不够灵活、波束方向的调控不便，同一天线难以实现模态复用或模态子集复用，当信号波长较长时对天线尺寸的要求较大，不便于其移动等。

图5 波束移相法产生涡旋电磁波示意图

5.1.2 信号域移相法

该方法通过对信号附加移相因子，并将移相后的信号作为均匀圆阵列(Uniform Circular Array,UCA) 阵元的激励，利用各阵元波束的空间叠加实现涡旋电磁波波束[25]。

目前，对UCA阵元激励附加相位的方法主要有射频域信号移相方法与基带域信号移相方法。其中，射频域信号移相多采用Butler移相馈电网络[46]或Rotman透镜[47]实现，如图6所示。

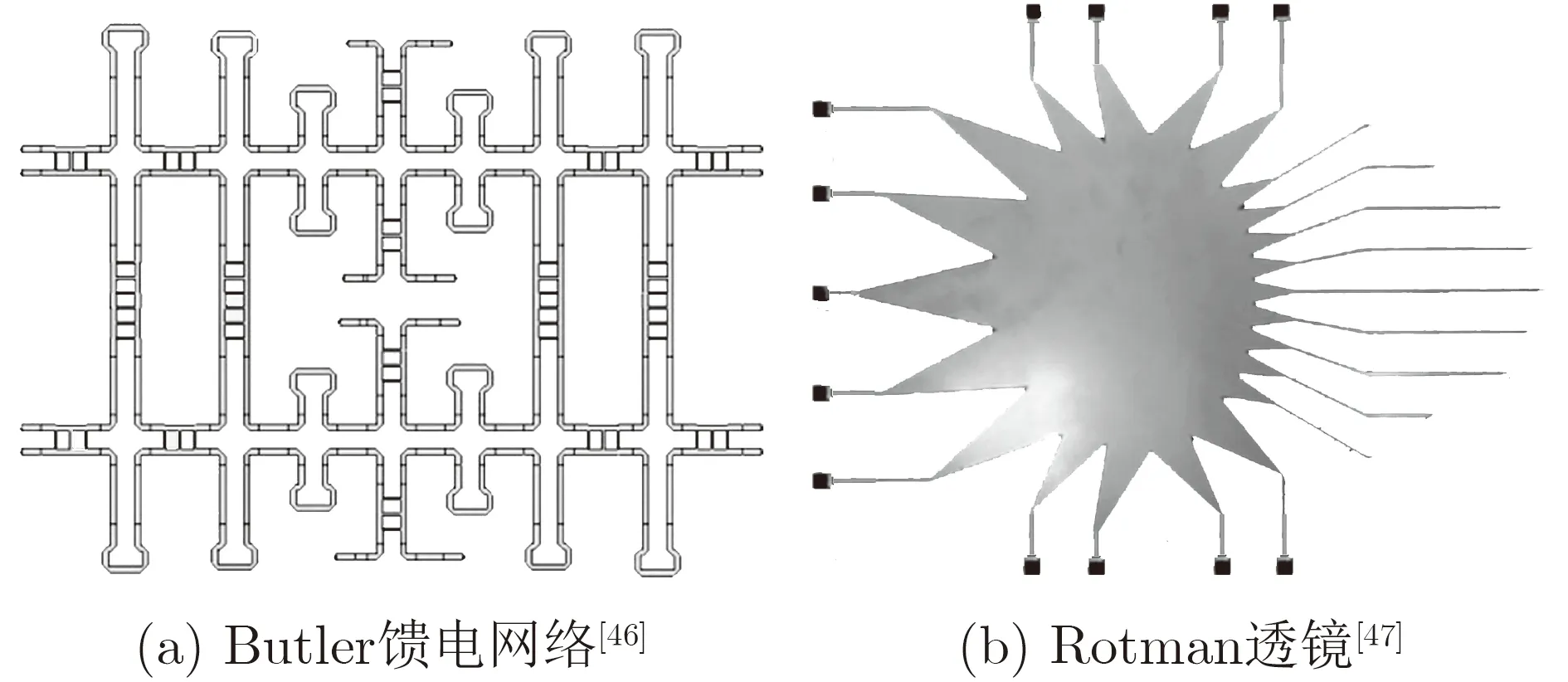
图6 射频域信号移相馈电网络示意图

与射频域信号移相电路网路复杂相比，在基带域易于实现信号的移相。研究表明，在基带域通过傅里叶相位序列[48]可产生模态复用涡旋电波波束。由于UCA阵列产生的涡旋电磁波的波印廷矢量中没有Pz分量，因此该波束属于“平面”的[49]。值得研究的是，将傅里叶相位序列改为Zadoff-chu序列[50]，可由UCA阵列产生另一种非中空的涡旋电磁波波束，相比之下，该波束更适合较远距离传播。

5.1.3 其它方法

包括圆环行波天线[51]与金属环开槽天线[52]。如图7所示圆环行波天线涡旋电磁波产生方法，对天线激励信号附加与模态相关的连续相位I0e−jℓφ实现不便，目前多见于微波波段使用。

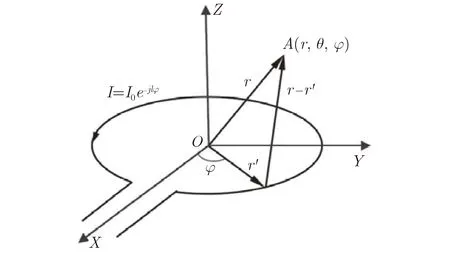
图7 射频域信号移相馈电网络示意图[52]

5.2 涡旋电磁波的接收

5.2.1 部分方位角采样接收的梯度检测方法

部分方位角采样接收的梯度检测方法[25,52]的基本的原理如图8所示。

图8所示的部分方位角采样接收的梯度检测方法是通过波束孔径上两个采样接收点的响应存在的相位差 ∆ϕ， 由ℓˆ=∆φ/β对涡旋电磁波携带的模态信息进行估计。该接收方法不支持涡旋电磁波的振幅、相位与频率均携带信息，不支持模态复用。

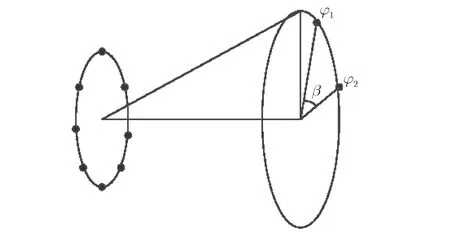
图8 相位梯度检测方法示意[25]

5.2.2 部分方位角采样接收的模态正交分离方法

部分方位角采样接收的模态正交分离方法[53]如图9所示。

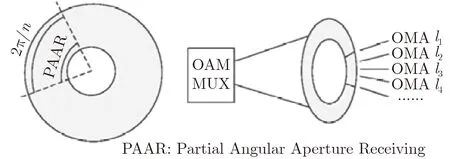
图9 部分方位角接收示意图[53]

部分方位角接收的模态正交分离方法的数学模型为

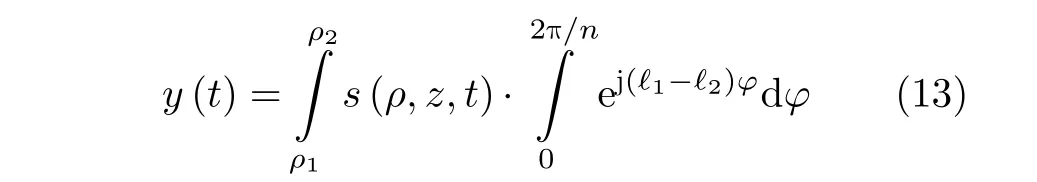
显然，当(ℓ1−ℓ2)可 被n整除时，将不能对信号模态信息实现正确分离。

5.2.3 全方位角采样接收的能量检测方法

全方位角采样接收如图10所示[54,55]。该方法首先对阵元接收的响应{y0,y1,...,yN−1}做关于模态ℓi的 FFT变换，得到，再由式(14)对模态信息进行估计。

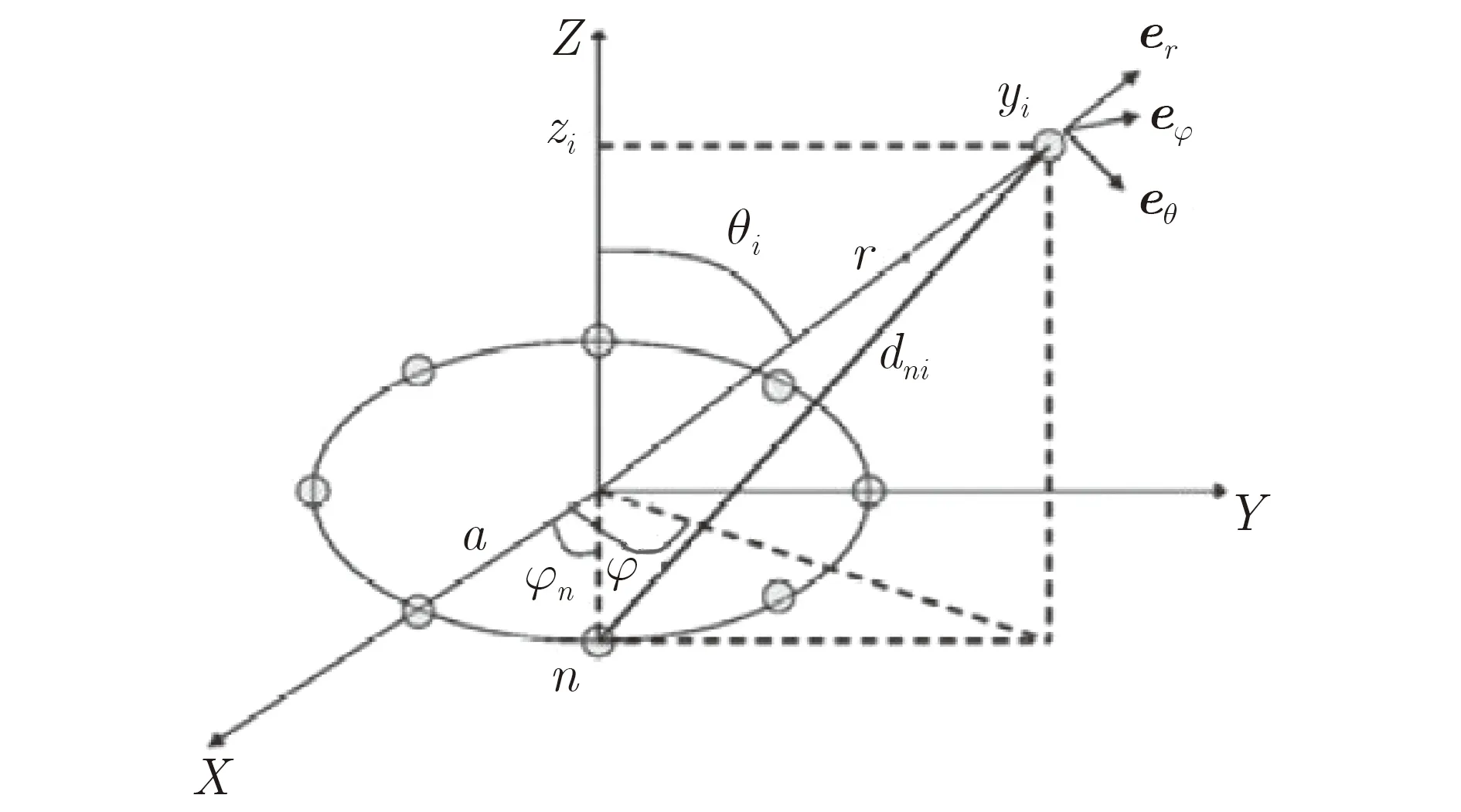
图10 全方位角采样接收方法示意图[54]

显然，全方位角采样接收是适合UCA阵列的，但能量检测却限制了涡旋波信号的振幅、频率与相位“3个维度”携带调制信息。

5.2.4 其它方法

包括光波段的螺旋介质透镜实现的电磁波模态方法[56]与全息干涉方法[57]。由于这两种涡旋电磁波信号传递方法中螺旋介质透镜的尺寸或干涉图样的尺寸与信号的波长呈正比，因此在无线射频领域鲜有应用。

综上所述，无线通信系统使用UCA阵列实现涡旋电磁波信号传输是可行的、便捷的。但远距离、非理想信道下涡旋电磁波信号的传输需解决信道衰落与波束汇聚等问题[58-60]。

6 涡旋电磁波与 MIMO 的兼容性研究

2011年，文献[56,61]报道了UCA阵列的OAM MIMO系统是单输入单输出(Single Input Single Output, SISO)通信系统的一种自然应用。该结论很快在学界引起争议，究其原因文献[56,61]没有认识到涡旋电磁波波前具有的特殊“极化纹理”，因此，该研究中所用信道矩阵并未充分反映涡旋电磁波信号的传输信道。

2015年，文献[62]以螺旋反射面天线[41]构建了空分复用涡旋波OAM MIMO室外演示系统验证，如图11所示。同年，文献[63]对螺旋反射面天线的圆周布局视距传播条件下的OAM MIMO的信道容量进行了仿真。

图11 3个OAM复用的MIMO链路示意图[62]

2018 年，文献[64]研究了UCA分形嵌套阵列的模态(子)集复用OAM MIMO无线通信系统架构，并在视距 (Line Of Sight, LOS) 传播条件下对信号产生、接收与模态并行分离进行了建模。

2019年，文献[65]以同心UCA阵列，如图12所示，研究了5模态复用时OAM MIMO系统的误码率。

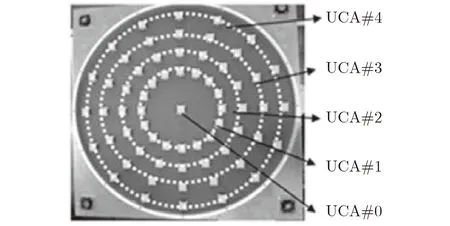
图12 同心圆嵌套时的模态复用OAM MIMO系统示意图[65]

7 涡旋电磁波无线通信的实现验证研究

7.1 光领域的实践研究

涡旋光通信按照信号传播介质不同，可分3个应用场景：

(1) 以光纤为代表的恒定介质[66]，该场景中多使用了介质透镜实现OAM模式的转换进行信息传递的，如图13所示。

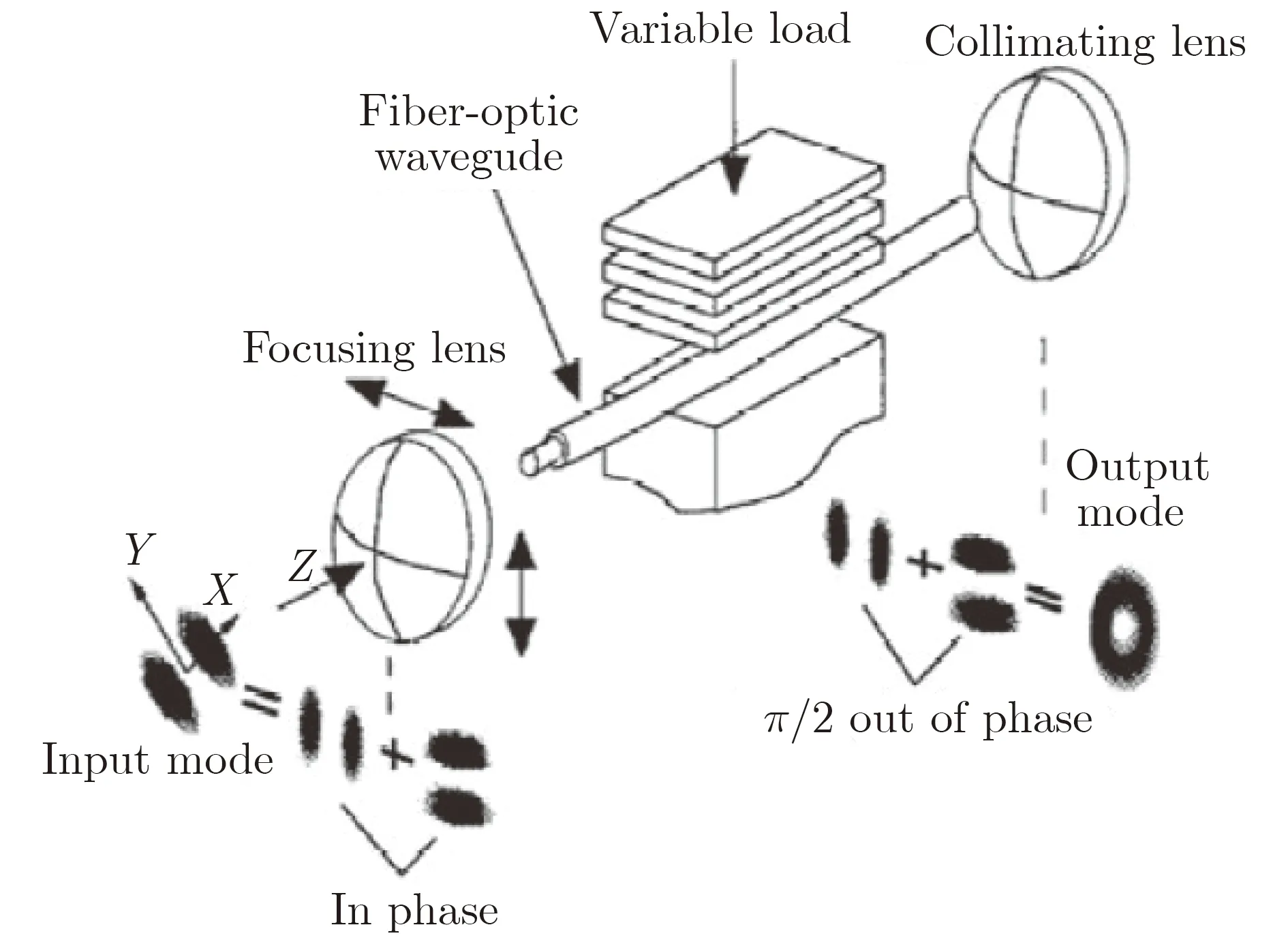
图13 OAM光通信方案示意图[66]

(3) 水下涡旋光通信。2016年，文献[71]报道了2模态(ℓ=−8,+8)涡旋光水下演示验证系统，其通信链路总长2.9 6 m，数据总传输速率为3 Gbit/s(1.5 Gbit/s/Channel)，模态复用下各信道的平均误码率小于2.073×10−4。

7.2 无线射频领域的实践

2007年，文献[10]基于UCA天线在千兆赫兹频段仿真了涡旋电磁波波信号的产生。

2009年，文献[35]采用全息相位板在千兆赫兹频段产生涡旋电磁波实现了速率为的未压缩视频数据传输，研究了利用涡旋电磁波的可以实现通信系统的大容量传输。

2014年，文献[72]在28 GHz毫米波频段基于4模态(ℓ=−3,−1,+1,+3)复用与正交线偏振结合技术在 2.5m距离大气介质中实现了总数据传输速率32 Gbit/s的涡旋电磁波无线演示系统。该系统采用16QAM/Channel调制，调制符号传输速率为1.0 Gbaud/s/CHannel，实测各信道的平均误码率均低于3.8×10−3。

2016年，文献[73]在60 GHz毫米波频段基于螺旋相位板实现了2模态(ℓ=+1,+3)与两极化方式复用的涡旋电磁波数据传输实验系统。该系统使用了16QAM/Channel 调制且调制符号速率为20Gbaud/s/Channel，获得了32 Gbit/s的等效数据传输速率，各信道测试平均误码率同样不大于3.8×10−3。

对比文献[72]与文献[73]的研究成果后可以发现，当系统的总数据传输速率不变时，改变涡旋电磁波模态复用增益N到 2N，则系统的频带消耗可由WHz缩小到W/2 Hz。若将其使用的电磁波替换为平面电磁波时，文献[74]可知，文献[72]所述系统的信道总数将由8个缩减到正交极化区分的2个；同样，文献[73]所述系统的信道总数也降到2个。在不考虑信道误码率变化前提下，文献[73]与文献[74]中所述系统的数据传输速率将分别降为8 Gbit/s与16 Gbit/s。

2015年，文献[75]采用环形腔谐振器行波缝隙天线在设计了两个不同的OAM信号同轴传输的室内演示验证系统如图14所示。在该系统中，一路OAM 携带高清视频信息，另一 OAM 携带方波信息。若模态复用数量增加，则文献[75]实现的环形腔谐振器的行波缝隙天线及其附属系统将变得较复杂。

图14 双模态无线室内演示系统示意图[75]

同年，文献[76]报道了基于折叠反射阵列天线在Ka波段涡旋电磁波数据传输。该天线结构具有纵向尺寸小、效率高等特点。由于天线反的体积和重量较大，降低了其可移动性，且该方法并不能解决反射波束对馈源的固有影响。

2017 年，文献[77]研究了UHF(Ultra High Frequency)波段涡旋电磁波能量传递问题，并选载频为870 MHz 通过交叉极子与一个不接触的铜环构建了一个涡旋电磁波能量传递系统。

2018 年，文献[78]认为基于OAM的模分复用(Mode Division Multiplexing, MDM ) 是LOS 路径下无线通信的一种调制方案，理论分析了该方案具有误码率低的特点。

综上所述，有：

(1) 光学领域对OAM的研究对无线射频领域具有引领作用；

(2) OAM在无线射频领域具有实现通信系统超大容量信息传递的潜能；

(3) 无线射频领域，模态复用的涡旋电磁波信息传递需要灵巧化的信息加载与提取方法；

(4) 目前涡旋波模态复用信息传递系统的传输距离较短。

8 结束语

通过文中分析，涡旋电磁波的轨道角动量使其波前呈现与其模态相关的“极化纹理”。通信领域，对涡旋波信号的识别与模态分离可从这个“极化纹理”着手。尽管涡旋电磁波的无线通信技术取得了一些进步，但是要实现OAM模态复用与无线MIMO系统的结合，尚需解决其信号分离、波束汇聚等诸多问题。探索以Zadoof-chu为代表的多相序列产生的非经典涡旋电磁波波束对无线通信系统而言更具有意义。跟踪并研究涡旋电磁波无线通信技术具有科学意义与工程需要。