基于多重分形去趋势波动分析的脑电信号特征提取及分类方法

陈敬凯，孟雪，王常青，钟亚鼎

1.安徽医科大学生物医学工程学院，安徽合肥 230032；2.安徽医科大学第一附属医院放射科，安徽合肥 230032

前言

脑电活动与大脑的生长及发展状况有着密切的联系［1-2］。对脑电信号的研究探索是认识脑活动机制、人的认知和学习机理机制、人的脑活动与机体活动的关系以及诊断脑部和精神疾病的重要手段，利用计算机技术对脑电信号进行处理和分析可以为医生提供快速有效的诊断依据［3-5］。关于脑电信号的特征提取与分类方法已经有许多学者做出了很多成果。较常见的处理方法有时频域分析［6］、小波变换［7-8］、人工神经网络［9-10］、支持向量机［11-13］和非线性动力学分析［14-15］等。但现有的脑电数据普遍存在维度高，数据难以预测解释等特点，如何提高分类准确率和算法的稳定性是脑电信号分类研究中需要继续思考的问题。

本研究利用多重分形去趋势波动分析算法（Multifractal Detrended Fluctuation Analysis,MF-DFA）来提取多标度特征，并将其与长短时记忆网络（Long Short-Term Memory Network, LSTM）结合起来对脑电信号进行分类，最后通过相关的实验来验证该方法的有效性和可行性。实验流程如图1所示。

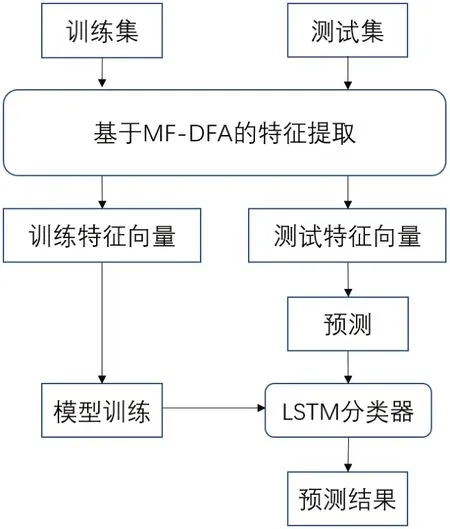
图1 分类实验流程图Fig.1 Flowchart of classification experiment

1 MF-DFA分析

MF-DFA 是由Kantelhardt 等［16］提出的一种可以用于分析脑电信号多标度特征的分析方法。通过该方法可以得到信号样本的多重分形谱，即广义Hurst指数hq 与广义维数Dq之间的函数关系，然后从中找出信号样本类间差异较大的标量作为特征向量用于分类器分类［17-19］。

对于长度为N的时间序列{xk} ，k= 1,2,…,N，MF-DFA计算步骤如下：

第一步，计算序列样本{xk} 的平均值：

第二步，确定信号样本的累计离差：

其中，i= 1,2,…,N。

第三步，将第二步所得的累计离差序列Y(i)划分成Ns个小区间。其中如果N不能整除s，Y(i)将会有一段数据没有被使用。为了能够充分利用数据样本而不造成数据丢失，需要对序列的剩余部分重复这一划分过程。最终得到2Ns个等长小区间，将数据样本的所有数据都充分利用起来以达到最佳效果。

第四步，将第三步中划分所得的每个等长小区间内的s个点进行最小二乘法的k阶多项式拟合：

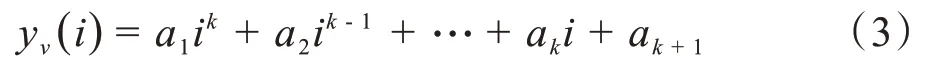
其中i= 1,2,…,s；k= 1,2,…。

第五步，计算均方误差。 设区间为v=1,2,…,2Ns，计算均方误差F2(s,v)：

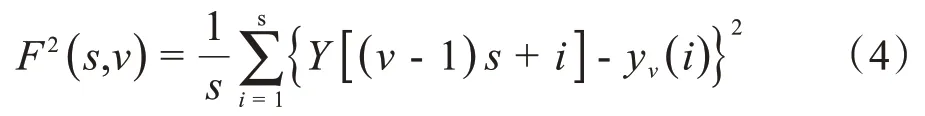
当v=Ns+ 1,Ns+ 2,…,2Ns，计算均方误差F2(s,v)：

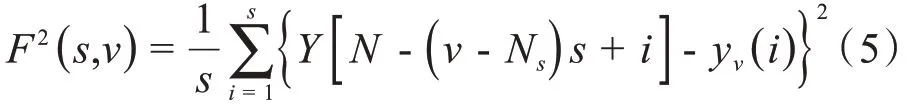
第六步，对去趋势后的F2( )s,v取平均值，则可得到q波动函数Fq( )s：

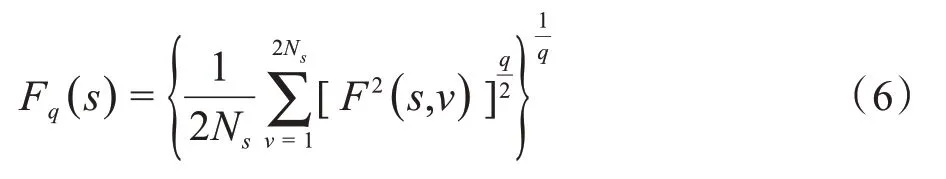
其中，q为任意不为零的实数，Fq(s)随着s的增大，以幂律关系递增，即Fq(s)∝sh(q)。则对应每一个s，都有一个对应的函数值Fq(s)，对于ln[Fq(s)]—lns函数关系图中的斜率即为广义Hurst 指数hq。不同阶波动函数下Fq和s间的关系如图2所示。q阶广义Hurst指数hq与阶数q的关系如图3所示。

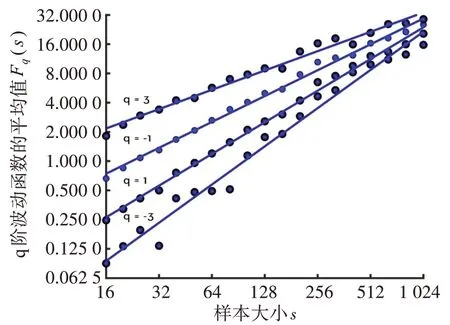
图2 不同阶波动函数下Fq与s间的关系Fig.2 Relationship between Fq and s under different order wave functions

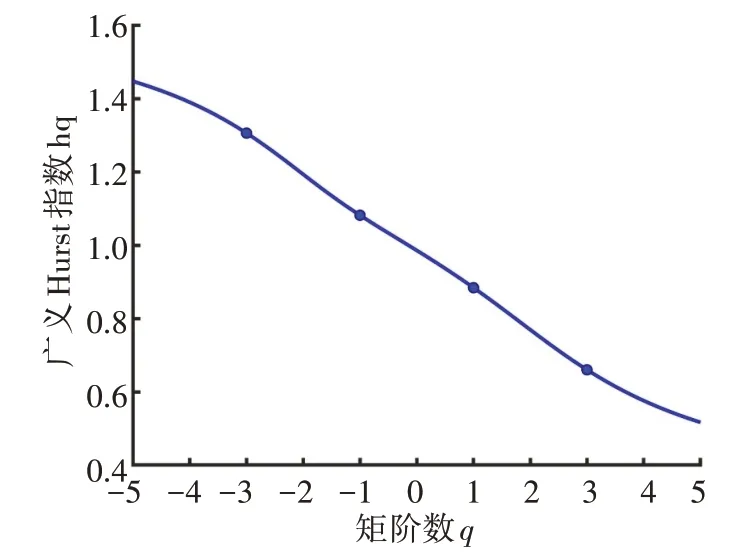
图3 广义Hurst指数hqFig.3 Generalized Hurst exponent hq

第七步，计算质量指数：

第八步，计算广义维数：

通过上述计算过程，可得出在波动函数不同的矩阶数q下信号样本的多重分形谱，如图4所示。

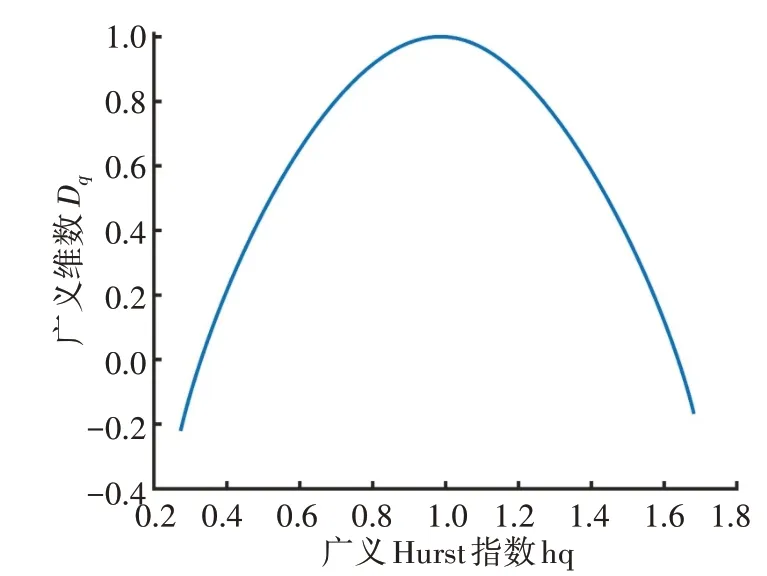
图4 信号样本的多重分形谱Fig.4 Multifractal spectrum of signal samples

2 LSTM分类训练与测试

LSTM 是对循环神经网络（Recurrent Neural Network,RNN）进行改进之后的结果［20-21］,因此，它的网络结构和模型参数都与RNN 很相像。LSTM 和RNN在深度学习中常用于处理时序信息。

本研究采用LSTM 对MF-DFA 所提取的多重分形特征向量进行分类训练和测试。使用数学工具Matlab 中的深度学习神经网络设计工具箱来设计LSTM分类模型，结构如图5所示。

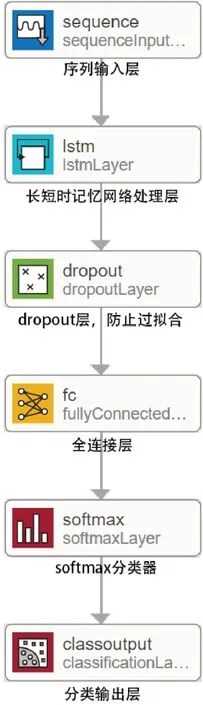
图5 LSTM 结构示意图Fig.5 Schematic diagram of long short-term memory network(LSTM)structure

LSTM 的核心第一层的特征序列输入层和第二层的LSTM处理层和最后一层的分类输出层，第一层输入层将脑电信号的特征向量导入神经网络。第二层LSTM层对特征向量进行分析，找出其中的相关性用于数据分类，最后一层的分类输出层会输出分类结果。

LSTM 的运作从序列输入层输入特征值序列开始，然后是LSTM 层对输入的特征序列进行分析。LSTM 的用途是对信号样本进行分类，所以该网络的末尾是一个分类输出层classoutput。中间加了一个dropout 层是为了防止过拟合的情况出现，此处dropout的可能性参数为0.5。

3 实验结果与分析

3.1 数据描述

实验数据为波恩大学医院临床采集的癫痫脑电数据集。该数据集由5个子集组成。每个子集由100个数据样本构成。每个子集对应一种类别的脑电信号，分别为Z类、O类、N类、F类、S类。

针对Z类和S类两种类别的脑电信号进行分类实验，其中Z类数据为正常人的脑电波，而S类数据为癫痫患者发病时的脑电波。两类样本示例如图6所示。

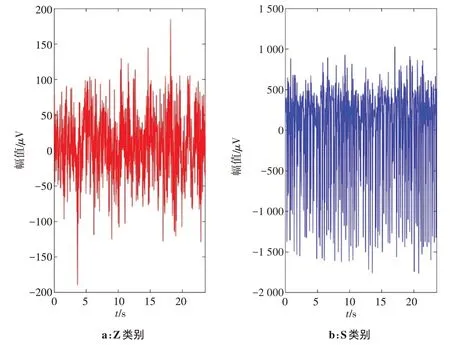
图6 Z与S两类脑电信号示例Fig.6 Examples of two types of EEG signals,namely Z-type and S-type

3.2 脑电信号的特征提取

此次实验是对特征提取方法和分类器的有效性和可行性进行探索，因此首先利用MF-DFA对脑电信号进行特征提取，然后进行脑电信号分类。从Z类和S 类中各取两个样本进行MF-DFA 计算所得到的多重分形谱如图7所示。

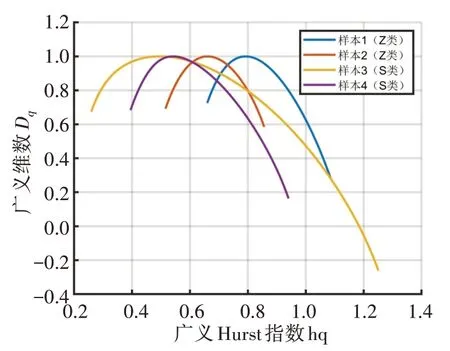
图7 Z类和S类中各取两个样本所得的多重分形谱Fig.7 Multifractal spectrum obtained by taking two samples in each of Z-type and S-type

4 个样本的多重分形谱中，根据Dq和hq 两者的变化，可以看到两个类别的样本有显著的不同。Z 类样本中hq 的最大值和最小值之差要小于S 类样本，同时hq 最大值和最小值对应的Dq值之差也要小于S类样本。每个样本数据的多重分形谱中可找到hq最大值对应的点、hq 最小值对应的点以及Dq最大值对应的点，这3个点基本可以反映出该样本数据的多重分形特征。从物理意义上讲，hq 最大值对应的点及最小值对应的点分别对应多重分形中的最大和最小奇异指数，分别展现了脑电信号在低概率测度子集和高概率测度子集的奇异程度。Dq最大值对应的点对应的hq 值，则为奇异性的值。值越小说明信号越平滑，反之，说明信号细节越复杂。因此，取这3个点的坐标作为该样本的特征，如样本1 的特征值为（1.086 5，0.272 1）、（0.790 1，1.000 0）、（0.659 9，0.725 3）。

3.3 分类实验结果

将100 个Z 类和100 个S 类样本数据按照不同比例划分训练集和测试集进行分类。LSTM 分类结果如表1所示。

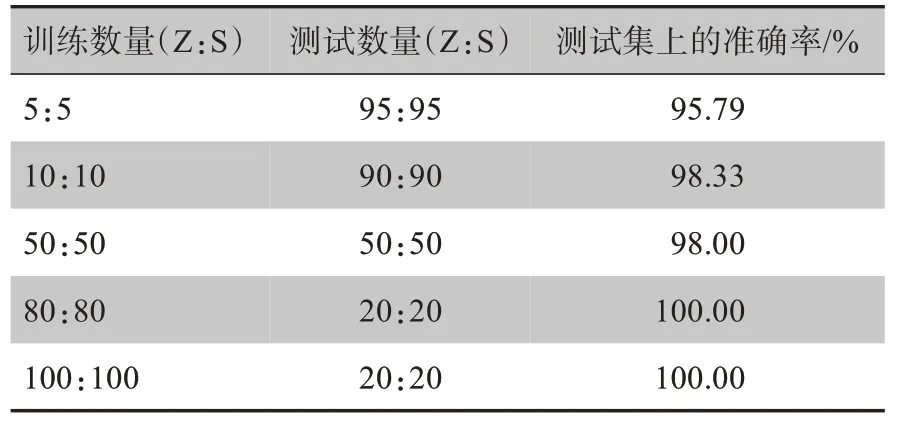
表1 LSTM 分类结果Tab.1 LSTM classification results

表1第一行表示从两个类别中各取5 个数据作为训练样本，另外的190 个样本作为测试集合，准确率为95.79%。以此类推，最后一行表示200个数据全部用来训练，再从中挑选20个数据进行测试，最后所得的准确率为100%。

从表1中可以看出，当训练样本达到20 个，占样本总数的10%，算法的准确率就可高达98%。当训练样本超过160 个，占样本的总数的80%，准确率达到了100%。可以看到分类器在不同比例的训练集和测试集中都有良好的表现并且具有较高的分类准确率和稳定性，该方法的有效性和可行性得到了验证。

4 结语

对脑电信号进行特性分析和分类研究对人类认知大脑运行机制和处理相关疾病具有重大而深远的意义。实验使用波恩数据集中的癫痫患者和健康者的脑电信号样本进行二分类，对算法的有效性和可行性进行了验证。通过对每个脑电数据样本进行特征提取来实现通过少量的数据反映样本的特性，大大降低分类器学习过程中的计算量，也可以防止无意义数据对分类器的影响。MF-DFA 提取出的特征向量能够很好地反映信号样本的差异。并且，在特征提取的时间成本上，MF-DFA 分析算法要远小于其多种特征分析算法组合。因此，该方法还存在计算量少、特征数据少、耗时少，且物理意义清晰的优势。LSTM 一般直接用来对时间信号样本进行分类训练和测试，不过这样会因为时间信号纬度高体量大的特点，使得网络的训练成本非常高，需要耗费大量的时间进行迭代的同时，成功率也只有90%［22］。本研究将MF-DFA 和LSTM 结合起来用于脑电信号的分类实验，将分类器的训练成本极大降低，成功率也大幅提升。该结果为癫痫疾病的精确诊断提供了有效的辅助信息，也为脑电信号的异常检测提供参考依据。