化学平衡中若干问题浅析

高树林，李艳妮，马银海，姜 雯

(昆明学院 化学化工学院，云南 昆明 650214)

化学平衡属于热力学基本原理应用之一，在物理化学中占有重要的地位.文中列举了化学平衡中几个重点和难点问题并进行了讨论，希望对物理化学的教学或学习有所帮助.

1 摩尔反应Gibbs自由能变(ΔrGm)与标准摩尔反应Gibbs自由能变

化学反应发生时，原子或电子之间重新组合，不仅分子的种类和数目发生的变化，而且分子的聚集方式也可能发生变化.显而易见，发生化学反应的系统为组成可变系统，需要用到化学势来解决变化的方向和限度问题，对于只做膨胀功的系统

dG=-SdT+Vdp+∑μBdnB.

(1)

若系统中有多个相α，β，…，应有：dG=dGα+dGβ+…[1].在等温等压条件下，上式变为

dG=∑μBdnB.

(2)

在一巨大系统中，当反应进度Δξ=1 mol时，ΔnB=νB.某物质的化学势是温度，压力和浓度的函数.由于系统巨大，反应前后各物质的浓度(基本)保持不变，因此化学势也不变，对(2)两边同时积分得

ΔrGm=∑νBμB.

(3)

把dnB=νBdξ代入(2)式有

dG=∑νBμBdξ.

(4)

上式两边同除以dξ，与(3)式联立可得

(5)

定义气体的活度为aB=fB/p⊖[2]，则化学势的表示通式为

(6)

把上式代入(3)式右边整理得到

(7)

令

(8)

(9)

(10)

此式即为化学反应等温式.在等温等压不做非体积功条件下， ΔrGm的值可以解决化学反应的方向和限度问题.

1.1 物理意义

1.2 影响因素

化学势是对某相某物质而言的，是强度性质的状态函数.若某相中有k种物质

μB=f(T,p,x1,x2, …,xk-1)

(11)

根据(3)式，影响ΔrGm的因素主要有2个：νB和μB的值.①化学反应方程式的写法.例如，一个化学反应如果两边同时乘以一个常数，化学计量数νB会发生改变，因此ΔrGm的值也会改变；②温度、压力和浓度.根据(3)和(11)式，化学势μB是温度、压力和浓度的函数，因此这3个因素也会影响ΔrGm的值.

1.3 作为判据

2 活度商J与标准平衡常数K⊖

J的定义为(9)式，称为活度商.前面提到气体的活度定义为aB=fB/p⊖，对于实际气体和理想气体反应可分别用下2式表示

(12a)

(12b)

Qf和Qp又分别称为逸度商和压力商.当化学反应达到平衡时有ΔrGm=0，根据(10)式

(13)

把(13)式代入(10)式得到

(14)

(15)

当总压力p增加或减小的瞬间(“新状态”)，即平衡移动之前，可以认为xB是不变的.这样“新状态”J的变化(变大或变小)完全由p∑νB决定.例如，对于减分子反应(反应后气体分子数减少，∑νB<0)，如果增加压力则p∑νB变小，J也随之变小.对于实际气体尤其是高压气体反应，压力对J的影响情况要复杂一些，不能简单地套用上述规律.浓度不影响K⊖，但会影响J，这种情况这里不再赘述.

Kx= ∏xBνB.

(16)

根据pB=pxB，结合(12b)式不难得到

(17a)

(17b)

由式(17b)可见，Kx不仅受温度影响，也和总压力p有关.温度一定时，若∑νB<0，则增加压力Kx变大[4]，反之变小；同理，若∑νB>0，则增加压力Kx变小，反之变大.Jx形式上和Kx一样，但二者意义不一样，Kx是化学反应达到平衡时的∏xBνB，而Jx是反应某一时刻的∏xBνB.前面提到对于理想气体反应，式(17a)左边的J只受压力影响.笔者认为，温度和压力都不影响Jx，因为即便温度或压力改变，只要xB不变那么Jx= ∏xBνB就不会改变.把式(17a)和式(17b)代入(14)式得到[4]

(18)

在一定温度下，对于处于平衡态的理想气体反应，若∑νB<0(反应后气体分子数减少)，增加压力则Kx变大而Jx不变，ΔrGm<0则平衡正向移动，其它情况依次类推.

(19a)

(19b)

(20)

van’t Hoff等压方程为

(21a)

把(20)式代入上式得，

(21b)

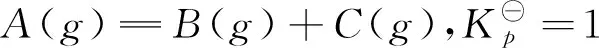
3) ΔrGm为多少?

或者采用第2)问的结果计算，注意到pi=ciRT，

4 结语