基于特征提取的工业控制系统入侵检测研究
倪 旻,曲金帅,范 菁,刘译文,李鸿,邱 阳
(1.云南民族大学 电气信息工程学院,云南 昆明 650504;2.云南民族大学 云南省高校信息与通信安全灾备重点实验室, 云南 昆明 650504;3.云南民族大学 云南省高校无线传感器网络重点实验室,云南 昆明 650504;4.云南民族大学 社会学院,云南 昆明 650504)
自第1次工业革命以后,工业控制系统(industrial control system,ICS)对于国家的建设起到至关重要的作用,包括石油、化工、电力、制造业等.随着信息技术的发展[1],越来越多ICS连接到外网,使得ICS容易受到入侵的威胁.
入侵检测系统(intrusion detection system,IDS)是通过监控和分析网络活动来检测网络异常最重要的安全机制之一[2].目前,IDS在工业网络中的应用越来越受到重视.与机器学习等领域相关的入侵检测技术正成为研究热点,归根结底就是模式识别中的分类.许多专家也提出了一些有效的工控入侵检测方法.陈万志等[3]利用白名单可以设置连续特征的特征范围和常见特征,神经网络则用于检测特征不完备或多特征异常情况,体现了入侵检测的有效性.於帮兵等[4]使用长短时记忆网络(LSTM)避免了梯度消失和记忆能力不足等问题,将SMOTE算法运用于少数类样本的采样,数据不平衡的问题迎刃而解,实现了对ICS良好的入侵检测.石乐义等[5]采用了相关信息熵,使其起到特征选择的作用,达到去除噪声,并针对不平衡样本采用Borderlines-SMOTE进行处理,同时在空间和时间维度上,CNN-BiLSTM模型提取数据特征,保证了良好的检测效果.Süzen等[6]提出了混合深度信念网络模型,即将低级特征结合起来,从少量特征中学习关键特征,这可以产生更好的分类性能.综上所述,现在研究者更多倾向于将机器学习算法引入到工控入侵检测领域,并取得了很好的效果,但是仍存在一些问题:例如在解决不平衡数据集上,所采用的方法没有考虑到不同少数类样本的分布情况;又如利用DBN可以提升入侵检测水平,但DBN隐含层的节点数量不容易确定,需要增加训练次数与手动调节次数,从而影响整个系统的网络训练过程等.
针对以上问题,提出了一种基于特征提取的ADASYN-PSO-DBN的工控入侵检测方法.
1 工业控制系统入侵检测模型
1.1 ADASYN
由于原始工控标准数据集中存在严重的不平衡性,仅正常事件就占据了总样本的63%.此外,部分类别的攻击事件中所占比例极低,这会导致ICS的大量正常事件会掩盖攻击事件,攻击事件没有得到正确和快速的识别,就会有更大的风险造成控制系统中断、关键基础设施破坏、经济损失和负面环境影响.因此采用自适应合成采样(ADASYN)方法来进行不平衡数据集的学习,ADASYN的基本思想是根据不同的少数类样本的学习困难程度使用加权分布.ADASYN方法不仅可以减少由于原始数据分布不平衡而带来的学习偏置,而且还可以自适应地转移决策边界集中在那些难以学习的样本上[7].这里的目标有2个方面:减少偏置和自适应学习.提出两分类问题的算法在ADASYN中得到了描述.
输入:具有m个样本{xi,yi},i=1,…,m的训练数据集Dtr,其中xi是n维特征空间X中的一个实例,yi∈Y={1,-1}是与xi相关的类标识标签.将ms和ml分别定义为少数类样本的数量和多数类样本的数量.因此ms≤ml并且ms+ml=m.
过程:
1) 计算类不平衡的程度:d=ms/ml.
(1)
其中d∈(0,1].
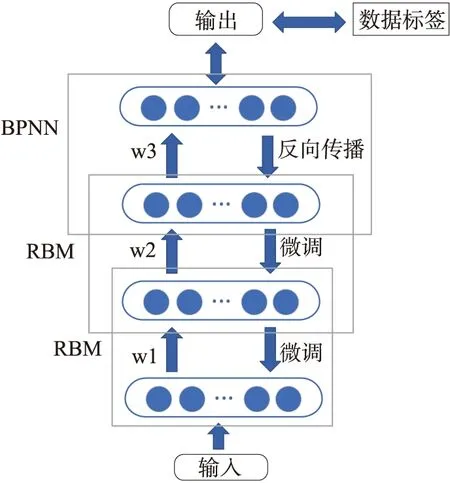
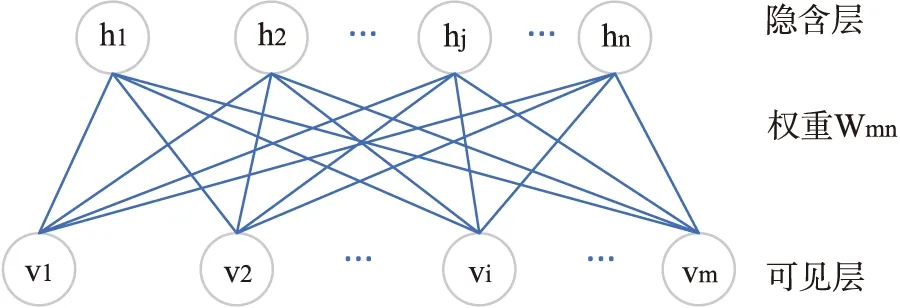
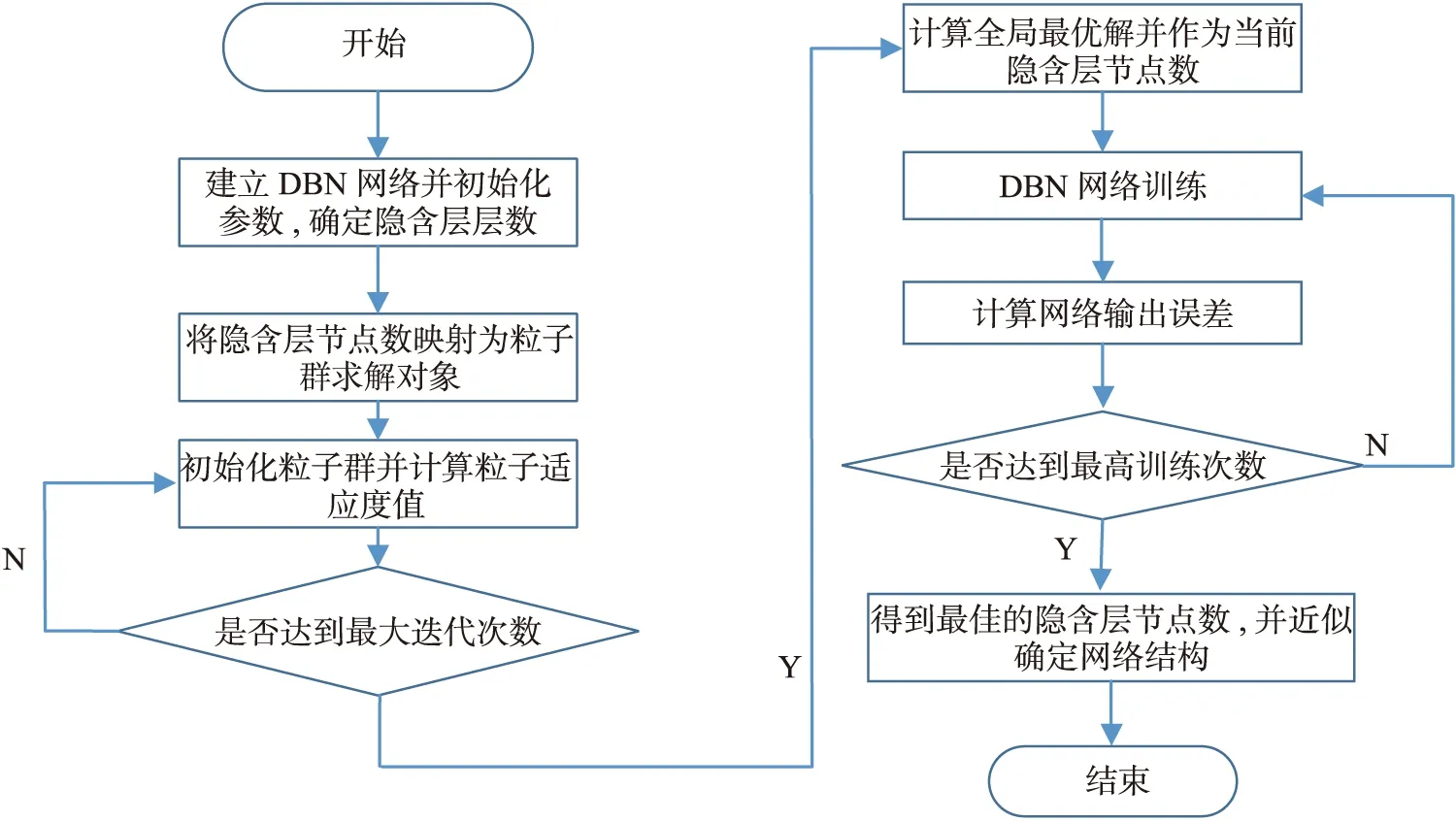
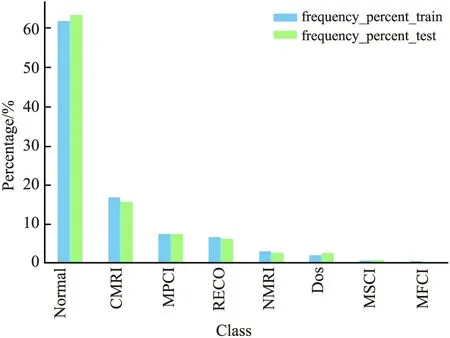
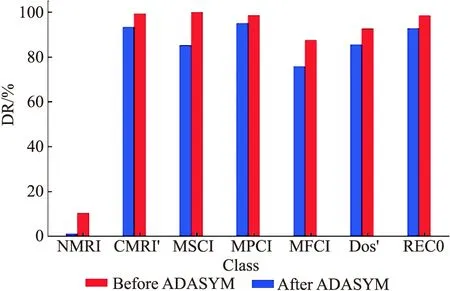
2) 如果d a.计算少数类需要生成的合成数据样本的数量:G=(mi-ms)×β, (2) 其中β∈[0,1]是一个参数用于指定合成数据生成后所需的平衡水平.β=1表示在泛化过程后生成一个完全平衡的数据集; b.对于每个样本xi∈minorityclass,根据n维空间的欧氏距离求K个最近邻,并计算其比率ri定义为: ri=Δi/K,i=1,…,ms. (3) 其中Δi是xi的K个最近邻中属于多数类的样本数,因此ri∈[0,1]; (4) e.对于每个少数类数据样本xi来说,根据以下步骤生成gi合成数据样本. 从1到gi的循环. (i)从数据xi中的K个近邻中随机选择一个少数数据样本xzi. (ii)生成合成数据样本: si=xi+(xzi-xi)×λ. (5) 其中(xzi-xi)是n维空间中的向量之差,并且λ是一个随机数:λ∈[0,1]. 结束循环. 随机森林(RF)是一种操作效率高、参数调整方便的集成学习bagging算法[8].决策树一般具有二叉树结构,是RF的基本模块.每个非叶节点根据特定的规则被划分为2个子节点,除非它是叶节点.类信息存储在叶节点中,叶节点可用于训练模型和断定分类结果. 使用单一决策树存在过拟合和精度方面的缺陷.RF算法可以使用由多个决策树组成的分类器解决该问题[9].RF过程包括以下主要步骤: 1) 随机森林决策树的构建 a.为每个决策树构建训练数据集 从具有N个样本的训练数据集中提取n个样本,构建一个决策树的训练数据子集.每棵决策树在RF中都有相应的训练数据集,如果RF中有ntree(树的数量),则需要使用bootstrap抽样方法建立相同数量的训练数据子集. b.将节点拆分成二叉树结构 从训练数据的M个变量中随机选择m(m c.重复步骤a和b,直到构建出一个随机的决策树森林. 2)分类 建立随机森林决策树的过程会产生一系列的分类器.多个分类器可以产生不同的分类结果.对于输入数据属于哪个类,采用多数投票原则来做出最终决定. 当RF应用于特征选择时,在每棵决策树中计算每个特征的排列重要性得分.在其他特征不变的情况下,RF算法计算每棵决策树的每个特征的排列重要性.排列重要性有3种值:正、负和零.随机重排后,重要特征对应的排列重要性应为正值.差的特征分散在不同的样本中,对应的排列重要性为负值.一个不相关的特征与样本上的标签没有任何相关性,相应的排列重要性总是为零.排列重要度得分越高,表示该特征越重要. 递归特征消除(RFE)是一种寻找最优变量子集的贪婪算法,其主要思想是反复建立一个模型,选择最佳(或最差)变量.移除特定的变量,然后重复上述过程,直到遍历所有剩余的变量.在这个过程中,变量是否被消除依据变量的重要性顺序.RFE方法需要一个机器学习算法来构建分类器并评估预测器的重要性.本研究采用RF方法作为RFE模型的分类器. 在RFE模型中首先选择的变量对后面选择的特征有显著的影响.由于RFE重采样过程中的分割差异,应用RFE方法,选择的变量是非唯一的结果.例如,第1个模型将包含所有输入变量,第2个模型将只包含有限的输入变量.针对上述问题,采用k-fold交叉验证和和模拟方法为工业控制系统入侵检测标准数据选择合适的特征变量.在每个交叉验证的RFE模型中,最优变量子集由最高的交叉验证精度确定. 1.4.1 深度信念网络 深度信念网络(DBN)是Hinton等的开创性成果,具有良好的分类性能.然而,DBN的网络结构一般是通过实践经验设定的.自2006年提出以来[11],它得到了广泛的关注,并成功应用于语音识别和入侵检测领域.从结构上看,DBN分为多个RBM与一层BP神经网络,结构如图1所示. 图1 深度信念网络结构 深度信念网络的训练步骤可以分为2步: 步骤1 逐层训练RBM.隐含层向量可以通过映射下一层的每个可见层向量得到,然后将隐含层向量作为下一层的可见层向量输入.根据可见层和隐含层之间的相关性,不断更新每一层的权值,然后通过类比训练多层RBM.在训练过程中,将第一层的误差按顺序传输到RBM的最后一层. 步骤2 在最后一个RBM后加入一个BP神经网络,以最后一个RBM的输出向量作为其输入向量.并将带标签的数据附加到该层,从上到下监督整个网络,调整整个网络的权值来微调深度信念网络. 1.4.2 受限玻尔兹曼机 受限玻尔兹曼机(RBM)是DBN的重要组成部分,它广泛用于数据分类、模式识别.它的第1层是可见层(v),其中包含大量可见单元,另一层是隐含层(h),其中包含大量隐含单元.RBM是一个无向图模型[12],模型的同一层中的节点之间没有连接,不同层之间相互连接,RBM结构如图2所示,W代表可见层和隐含层之间的连接权重,以及所有可见层和隐含层之间都存在连接.而可见层单元不像隐含层那样相互连接. 图2 受限玻尔兹曼机结构 RBM是一种双层随机神经网络,它包含一层表示数据的可见节点(υ1,υ2,…,υi,…,υm)和一层学习表示特征的隐藏节点(h1,h2,…,hj,…,hn),每个υi∈{0,1}和hj∈{0,1}.定义可见节点的偏置为(b1,b2,…,bi,…,bm),隐含节点的偏置为(c1,c2,…,cj,…,cn).联合配置{υ,h}的能量函数E(υ,h)定义如下[13-14]: (6) 训练完一个RBM后,可以在第1个RBM的基础上堆叠另一个RBM[15].第1个RBM中隐含单元的最终学习状态被用作第2个RBM可见单元的输入数据.因此,可以将多层RBM叠加,自动提取不同的特征,这些特征逐渐代表数据中更复杂的结构.在实践中,将RBMs堆叠起来,用贪婪的分层无监督学习算法进行训练.在训练阶段,每个添加的隐藏层都被训练为RBM. 1.4.3 反向传播神经网络 反向传播(BP)神经网络是在预测任务中应用最广泛的人工神经网络模型之一.在DBN中,最后一层是BP神经网络.接受最后一层RBM的输出特征向量作为这一层的输入特征向量[16],并监督整个网络结构是BP神经网络在DBN中的主要任务. 在DBN中BP算法的微调权值如下. 输入 训练样本xi(i=1,2,…,m). 初始化 从RBM的预训练中获取模型参数并初始化θ={wij,ai,bj},迭代数为k. 输出 微调权重后的模型参数为θ={wij,ai,bj}. 第1步 计算每个训练样本xi,实际输出yi. 第2步 对于每个输出单元k,计算实际输出和理想输出之间的误差梯度: δk←yk(1-yk)(xk-yk) . (7) (8) 第4步 计算每个网络模型参数: θij=θij+Δθij. (9) 式中:θij=ηyjδj,η为学习率. 第5步 存模型参数,确定是否达到迭代次数,或者转到第1步. 1.4.4 粒子群优化算法 通过探索鸟类群体觅食行为,衍生出了粒子群优化算法(PSO).粒子是对鸟类的模拟.每个粒子都可以看作是n维搜索空间中的一个搜索个体,每个粒子的当前位置是这个问题的候选解决方案[17].每个粒子都有两个属性:速度和位置.速度表示移动的步长,位置表示移动的方向.将每个粒子找到的最优解作为个体最优解,将所有粒子的最优解作为全局最优解.通过多次这样的迭代,速度和位置不断更新,当满足终止条件时,迭代将退出. PSO的过程可以描述如下: 1) 随机初始化搜索空间中粒子的速度和位置. 2) 定义适应度函数.每个粒子都有自己的最优解,对应于一个适应度值,而全局最优解则由这些最优解生成.每次迭代比较当前的全局最优值与历史的全局最优值,比较的结果将决定是否更新全局最优值. 3) 每个粒子的速度和位置的更新表示为: Vid=ωVid+C1random(0,1)(Pid-Xid)+C2random(0,1)(Pgd-Xid), (10) Xid=Xid+Vid. (11) 其中C1和C2是个体和群体学习因子,Pid是第i个粒子个体最优的第d维,Pgd是全局最优的第d维,ω为惯性权重,其线性衰减策略可表示为: (12) 其中iter是最大迭代次数,iteri是当前迭代次数,ωmax和ωmin分别是ω的最大值和最小值. 1.4.5 PSO算法优化DBN模型 DBN的运行过程是先通过RBM进行预训练,经过隐含层后通过重构误差对网络参数用BP神经网络进行微调,从而得到网络的整体结构,当准确率较高且返回误差稳定在较小值时,代表着当前DBN结构较好.因为在建立DBN模型时不能完全确认其隐含层的节点数,所以有必要增加训练次数,并手动调整网络节点数,以避免在训练过程中出现网络性能损失的问题,本文在DBN模型构建后利用PSO算法优化DBN的隐含层层数以及节点数,获得最优的DBN结构,得到最高的准确率. PSO算法优化DBN模型的步骤如下: 1) 构建一个DBN入侵检测模型并初始化网络参数,即确定网络中隐含层的层数和每层的节点数; 2) 初始化粒子群各参数,包括学习因子C1和C2、最大迭代次数iter、惯性权重ωmax和ωmin,同时规定粒子速度和位置的范围.在该范围内随机初始化种群中粒子的速度向量和位置向量.将DBN网络的各层间的连接权重映射到粒子的各维度; 3) 确定适应度函数,使用准确率(Accuracy)作为各个粒子的适应度函数值,求出个体极值Pid和群体极值Pgd; 4) 比较各粒子的适应度值与自身个体极值Pid的大小.若粒子当前的适应度大于个体极值Pid,则将其赋给个体极值Pid,反之保持Pid不变.设定DBN模型的隐含层节点数,对其进行训练并评估,判断准确率是否为最大值; 5) 比较群体中所有粒子的Pid与群体极值Pgd,若存在Pid优于群体极值Pgd,则将其赋给群体极值Pgd,反之保持Pgd不变; 6) 根据式(10)、(11)更新各粒子的速度和位置; 7) 确定迭代是否结束.当达到设置的最大迭代次数,或者群体极值的变化量足够小时,迭代结束.否则,返回步骤3; 8) 如果准确率增加到一定程度则满足最优解条件,将最终求得的隐含层节点数作为DBN模型的初始训练参数并近似确定DBN网络结构,直至达到DBN结束训练的要求,DBN网络建模完成. 整个流程如图3所示. 图3 PSO优化DBN模型训练过程 文中使用的是托马斯·莫里斯与他的研究团队于2014年在密西西比州立大学关键基础设施保护中心(MSU)从实验室环境中用串行端口数据记录器捕获的网络流量记录生成的工控标准数据集[18],数据源于天然气管道ICS网络层,该数据总量为97019,并进行了数值化处理.数据以X=(x1,x2,…,xn,y)的方式存储,其中x1,x2,…,xn为每条数据的特征,y为每条数据的类别标签.本文所用数据集中的每条数据包含26个属性与1个类别标签.数据类别和相应标签值如表1所示. 表1 攻击形式及仿真分类标签 为了验证ADASYN-PSO-DBN在工控入侵检测中的有效性,随机抽取了原始数据中的 10 000 条数据,选取 8 000 条用于训练,2 000 条用于测试,采用5折交叉验证,其训练数据与测试数据分布如图4所示.所采用的实验平台:Inter Core i5-5200U CPU 2.20GHz,4G内存,Anaconda3 Spyder.PSO算法初始参数设置为:种群大小为20,最大迭代次数为20,ω=0.5,C1=0.5,C2=0.5. 图4 不同类型的数据分布 文中为了评估模型的性能,评价指标为以下6种:准确率(accuracy)、检测率(DR)、精确率(precision)、召回率(recall)、误报率(FAR)、运行时间. (13) (14) (15) (16) (17) 其中TP是被正确归类为攻击的攻击数据,TN是被正确分类为正常的正常数据,FP是被错误归类为攻击的正常数据,FN是被错误归类为正常的攻击数据. 实验的软件环境是基于TensorFlow的Keras深度学习配置.实验过程中,用DBN训练数据集,因此对模型的部分参数进行了设置,如表2所示. 表2 DBN实验参数 为了验证工控入侵检测模型的有效性,本文进行了多组实验,包括采用ADASYN合成少数类前后的效果对比;采用基于随机森林(RF)的特征提取;以及通过PSO优化得到的DBN最佳隐含层层数以及节点数,并用该DBN模型进行对比;记录每次所得结果,将所有评价指标汇总并取均值,实验共进行10次. 2.3.1 ADASYN合成少数类前后效果对比 由于数据存在不平衡的问题,将经过处理前后的数据集在PSO-DBN模型上进行验证.实验结果表明,经过ADASYN处理的数据集有效提高了各类型数据检测率,虽然NMRI检测结果有所降低,但是几乎提升了整体的性能,结果如图5所示. 图5 ADASYN处理前后的效果对比 2.3.2 基于随机森林与递归特征消除的特征选择 本文采用基于随机森林(RF)与递归特征消除(RFE)的方法对数据进行特征选择,因为所用的数据集自然包含一些不相关且有噪声的特征,这些特征会降低算法的有效性,导致检测性能较差,所以先应用RF对数据集中26个特征进行特征重要性排序,排序结果如图6所示,由此通过特征排序可以清晰发现特征的冗余,进而进行下一步的特征选择. 图6 特征重要性排序 根据以上的特征重要性排序,应当选取特征个数为15,以上更为重要的15个特征需要经过RFE方法进行选择,特征选择前后的入侵检测性能对比如表3所示,可以看出检测的准确率明显提高,平均运行时间降低. 表3 特征选择前后的实验结果 2.3.3 经过预处理后的PSO-DBN工控入侵检测模型优化 设定好初始化参数后针对DBN隐含层层数是影响入侵检测效果的重要因素,实验对1~6个隐含层的DBN网络结构进行寻优,并进行准确率和检测率对比,最终得到最佳的隐含层层数以及每层的节点个数,如表4所示. 表4 不同结构对应的准确率和检测率 实验结果表明,随着DBN网络层数的增加,综合准确率与检测率都有所提升,DBN的最佳网络结构是26-110-63-31-8,综合准确率达到95.62%,检测率达到93.68%,但在逐步增加隐含层的情况下,准确率和检测率开始呈现下降趋势.在优化了DBN网络隐含层层数与节点数后,将最终模型的检测结果与其他基准入侵检测模型进行比较,这样更体现了该模型的优势.各个基准入侵检测模型的参数设置如表5所示.另外,为了保证实验的公平性,在同一环境下,对每种常用方法进行多次实验,对比结果如表6所示. 表5 各基准模型的参数设置 从表6可以看出,本文模型的分类准确率、精度以及召回率最高,达到95.62%、96.27%、93.68%,虽然本文模型高于长短时记忆网络(LSTM)的FAR,但是整体检测效果好于后者.综合各个指标发现,基于ADASYN-PSO-DBN构建的工控入侵检测模型具有良好的检测效果. 2.3.4 各攻击类型数据检测效果分析 在工控入侵检测标准数据集中,有着1种正常运行数据和4种攻击类别,4种攻击类别细化为7种攻击形式.各模型识别8种类型的数据,检测率如图7所示. 从图7可以看出,ADASYN-PSO-DBN对每种类型的数据都具有较高的检测率,在识别MSCI、DoS、RECO上更为凸显.ADASYN-PSO-DBN与其他模型相比,整体在Normal、CMRI、MPCI、RECO类别的数据检测率较高,都在90%以上,尤其是在RECO攻击的分类识别上,各模型的检测率都接近100%,但是在识别NMRI上,识别检测率最高的只在50%以下. 为了解决不平衡、高维、非线性数据的入侵检测问题,本文提出了基于特征提取的ADASYN-PSO-DBN的工控入侵检测模型.通过ADASYN处理技术,对少数类样本进行过采样,在一定程度上解决了分类器倾向于多数类样本的问题.采用随机森林和递归特征消除方法进行数据特征提取和特征降维,达到去除冗余特征,加快检测效率.经过处理后,建立了PSO-DBN模型,利用PSO算法对DBN隐含层层数以及节点数全局寻优,从而增加DBN模型的入侵检测效果.仿真结果表明,与多种常用的入侵检测方法相比,该模型基本上在各攻击类型的检测上均具有较高的准确率.虽然该模型具有良好的检测能力,但是在识别NMRI时的检测效果需要进一步优化,这是下一步的工作.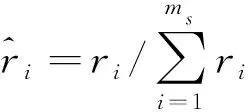
1.2 随机森林
1.3 递归特征消除
1.4 基于PSO的DBN工控入侵检测模型优化
2 实验与结果
2.1 工控入侵检测数据集与预处理

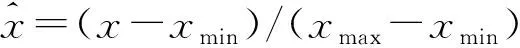
2.2 仿真平台设置和评价指标
2.3 实验过程与结果分析





3 结语

