基于构件冗余度均衡化的单层网壳结构优化研究

朱南海，李杰明

(1.江西理工大学江西省环境岩土与工程灾害控制重点实验室，赣州 341000；2.江西理工大学土木与测绘工程学院，赣州 341000)

结构构件的冗余特性是保证结构具有足够鲁棒性的重要指标之一，可以直观体现构件在结构中的重要性及其破坏后的影响。若各构件在结构中的重要性程度差别较大，当某些构件失效后，可能引起结构的连续性倒塌破坏。合理降低构件间的重要性差异，实现构件冗余度的均衡分布，如何定量评价构件冗余度是首先需要解决的问题。

目前国内外研究学者从多角度对结构构件的重要性评价方法进行了研究。早期Ghosn等[1]提出以结构超静定次数作为冗余度的定义，这也是冗余度最直观的定义。Pandey和Barai[2]通过分析结构响应对设计参数的灵敏度提出了构件冗余度的评价指标，叶继红等[3−6]在此方法的基础上对地震作用下网壳结构的构件冗余度进行了分析，并以此判断结构的重要构件。田黎敏等[7]基于构件移除后的构件应力、节点位移及结构承载力、自振频率、应变能等参数建立了构件重要性的衡量指标。蒋淑慧等[8]基于单元冗余度分布的均衡性提出了一种适用于杆系结构的构件重要性评估方法。黄靓等[9]以结构构件移除前后的承载力变化量与原结构承载力的比值评价结构构件的重要性。林旭川等[10]以广义结构刚度为基础判别构件在结构中的重要性。张立森等[11]将构件分项内力值之比作为结构构件重要性评价指标。文献[12 −13]提出了一种构件冗余度评价方法，并通过加强关键构件、削弱一般构件从而达到增强结构整体性能的目的。

本文将文献[12]提出的基于敏感性分析的构件冗余度评价方法应用到单层网壳结构中，以衡量构件在结构中的重要性，而后以构件的截面参数(如圆钢管构件的外径D和壁厚t)作为优化变量，采用粒子群优化算法，将构件间的冗余度偏差最小化作为优化目标，获得满足要求的构件截面参数最优值，从而实现结构整体性能和抗倒塌能力的提升。

1 静载下的结构响应灵敏度分析

静载作用下结构位移与荷载间的关系可表示为：

式中： K(θ)、 U(θ)和 F(θ)分别为结构整体刚度矩阵、节点位移向量和荷载向量；θ为结构设计参数。

当结构设计参数θ取为构件的材料弹性模量E 时，式(1)中荷载对结构设计参数E的灵敏度∂F/∂E恒为零，于是有[12]：

当矩阵K的逆存在时，可得结构的位移响应灵敏度为：

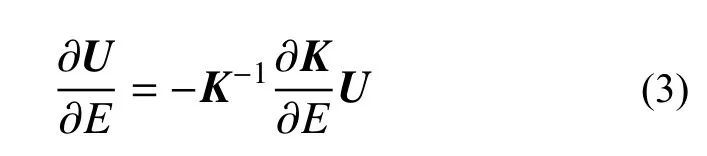
构件单元 j 的应变能可表示为：

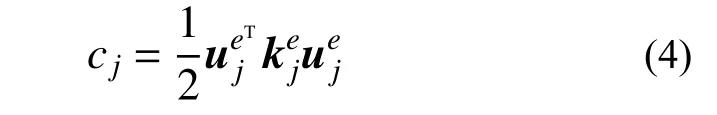
于是，构件 j 的应变能对构件 i 的材料弹性模量Ei的灵敏度为[12]：

式中， ∂uej/∂Ei为局部坐标系下构件 j的节点位移对构件 i的材料弹性模量Ei的灵敏度。

2 结构构件的冗余度定量评价

文献[12]通过分析构件应变能对其他构件刚度参数(材料弹性模量)的灵敏度及其移除后引起的结构应变能的改变量，将构件冗余度的衡量指标定义为：

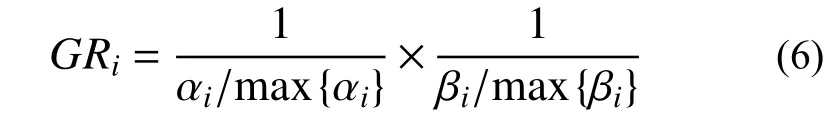
式中：αi为结构构件对构件 i刚度参数(弹性模量Ei)的累计应变能灵敏度；βi为构件 i移除后的结构应变能变化率。αi和βi可分别由式(7)和式(8)计算：

式中：ne 为结构构件数；SjiC 和为原结构和构件 i破坏后的结构应变能。

3 基于结构构件冗余度的均衡优化与实现

3.1 结构构件冗余度的均衡优化

3.1.1 优化目标的确定

由式(6)可获得结构构件的冗余度系数，其大小与构件在结构中的位置及截面尺寸有关，在保持结构形态不变的条件下，依据构件的冗余度系数值，将结构构件集Ω划分为：结构重要构件子集A、结构一般构件子集B及次结构要构件子集C。

设参数ξ1、ξ2分别为结构重要构件与一般构件、一般构件与次要构件的界限值，构件子集A、B、C的可由式(9)确定：

式中，参数ξ1、ξ2可按式(10)和式(11)确定：

式中： G Ri为构件 i 的冗余度系数；φ1、φ2为构件选取参数，φ1取0.01～0.015，φ2取2.2～2.8。

为避免个别构件破坏后可能引起的结构倒塌现象，应尽量缩小构件间的重要性偏差，使构件的冗余度能够均衡分布。由于各构件在结构中的作用不同，一方面应减小结构各构件的重要性差异，同时同类构件的重要性差异也应得到有效控制。将构件的截面参数(外径D 和壁厚t)作为优化变量，以减小结构各构件及同类构件间的重要性差异为目标，将优化目标函数定义为：

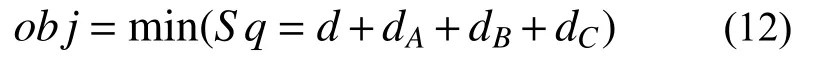
式中：d 为全体结构构件的冗余度标准差；dA为重要构件的冗余度标准差；dB为一般构件的冗余度标准差；dC为次要构件的冗余度标准差。

3.1.2 约束条件

1)构件长细比

根据《空间网格结构技术规程》(JGJ 7−2010)[14]对构件长细比的规定，构件 i 的长细比λi应满足：

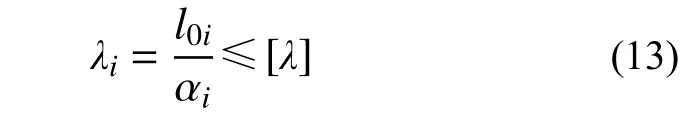
式中：l0i为构件 i 的计算长度；αi为构件 i的截面回转半径；[λ]为其容许长细比。

2)结构位移

同理，根据文献[14]对空间网格结构位移的要求，荷载作用下的结构最大位移应小于其允许值，即：

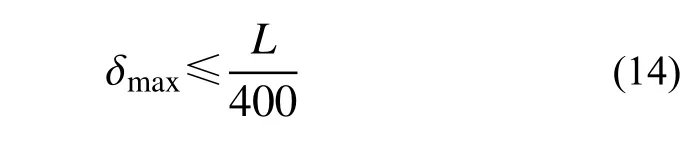
式中： δmax/m为结构的最大位移允许值；L为结构跨度。

3)材料用量

为满足结构的材料用量要求，以式(15)作为结构材料用量的限定条件，即：

式中： Veit为结构材料总用量； Ve0为结构材料用量允许值，本文将其设定为原结构材料用量。

4)构件强度与稳定性

在荷载作用下，构件的强度应满足《钢结构设计标准》(GB 50017−2017)[15]规定的要求，即：

式中：Ni/N为构件i 的轴压力设计值； Mxi/(N·mm)、Myi/(N·mm)分别为同一截面处绕x轴和y轴的弯矩设计值；Ai/mm2为构件 i 的截面面积；γm为构件截面的塑性发展系数，取为1.15；Wi/mm3为构件 i的净截面模量；f为钢材的强度设计值。

同理，根据文献[15]的相关规定，考虑轴力和弯矩共同作用，构件的整体稳定性应满足式(17)的要求：

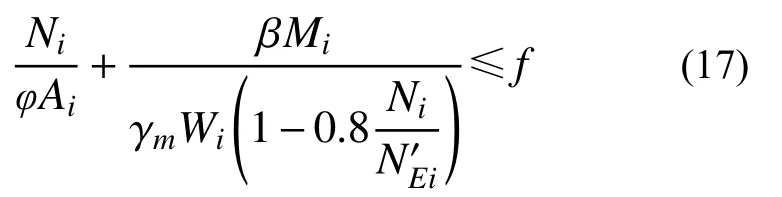
式中：φ为轴心受压构件的整体稳定系数；Mi/(N·mm)为构件 i 计算整体稳定时采用的弯矩值；β为等效弯矩系数；为构件 i的欧拉力[15]。

3.2 基于粒子群算法的结构构件冗余度均衡优化的实现

粒子群优化算法是一种基于鸟群捕食行为的智能寻优技术[16]，该优化算法在结构设计、优化等领域得到广泛的应用[17−21]。朱南海等[22]利用该算法对网壳结构构件的截面尺寸进行了优化，提高了结构的整体性能。本文以结构构件的截面尺寸为优化参数，以减小构件间的冗余度差异为目标，基于粒子群算法对构件的截面参数进行优化，减轻构件破坏后对结构承载力等性能的影响，其具体的优化过程及步骤如下：

步骤1：算法参数的设置

设参数P 、m 分别为待求解变量参数的数目和种群规模的大小， Vmax、 Vmin为搜索速度的界限值，c1、c2为学习因子，w为惯性系数。以文献[23]中给出的圆钢管型号为基础，选取其中的174种常用圆钢管型号作为构件优化的截面尺寸库并进行编号，这些圆钢管的外径和壁厚的取值范围分别为65.0 mm～180.0 mm和2.5 mm～15.0 mm。

步骤2：粒子初始化及其初始搜索速度的计算

以步骤1定义的174个钢管编号为基础，将构件截面尺寸的优化选择问题转化为钢管型号编号的搜索问题。初始种群中粒子个体Xs可由式(18)生 成，即 Xs=(Xs1,Xs2,···,XsP)， s=1,2,···,m，其各元素为对应的钢管型号编号。同时可由式(19)生成初始搜索速度，即 Vs=(Vs1,Vs2,···,VsP)：

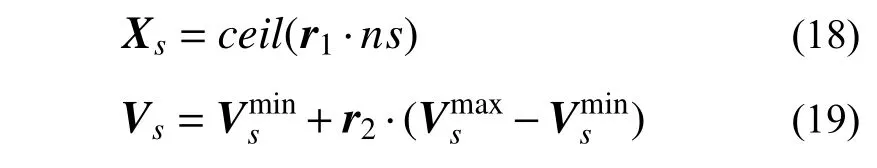
式中： ceil 为函数值取整；r1、r2分别为元素值介于0～1的P维随机向量；ns=174。

步骤3：粒子适应度值的计算与粒子更新

迭代步计算中，由式(12)可获得粒子群中各粒子个体的适应度值，通过比较粒子与个体最优粒子以及全局最优粒子的适应度值，对个体最优粒子和全局最优粒子进行更新，具体规则如下：

步骤4：粒子搜索速度与粒子种群的更新

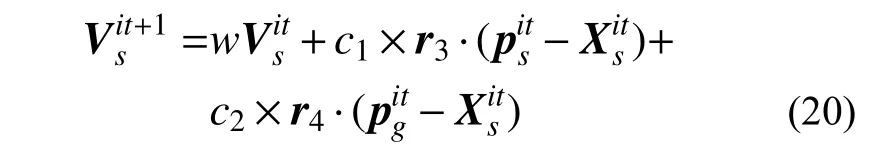
式中：w 为惯性权重；c1、c2为学习因子；r3、r4分别为元素值介于0～1的P维随机向量[24]。

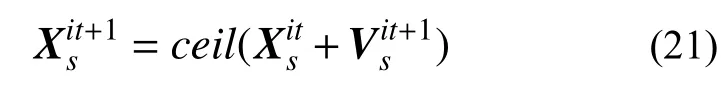
步骤5：计算结束条件

以最大迭代数作为算法终止条件，当迭代数达到设定值时，计算结束，获得结构构件截面尺寸的最优值。

以构件的截面尺寸为优化变量，将式(12)定义的构件冗余度偏差最小化作为优化目标，基于粒子群优化算法，减小构件间的冗余度差异，减小构件失效对结构的影响，其具体的实施流程如图1所示。

图1 构件冗余度均衡优化流程图Fig.1 The balanced optimization of structural component redundancy

4 算例分析

4.1 算例1：20 m跨K6N3型单层球面网壳结构

如图2所示一跨度为20 m，矢跨比为1/5的K6N3型单层球面网壳，支座为周边固支，节点为刚性连接，杆件采用圆钢管，其初始截面尺寸为80.0mm×3.0mm，材料弹性模量E为210.0 GPa及其屈服强度fy为235.0 MPa，作用于结构上的等效节点荷载值为15.5 kN。

图2 一K6N3型单层网壳结构 /mFig.2 A K6N3 single-layer reticulated shell

根据结构的特点，可将所有结构杆件分成5组，结构杆件的编号及分组(括号内的数值为结构杆件的分组号)如图3所示，优化中组号相同的杆件采用的钢管型号相同。

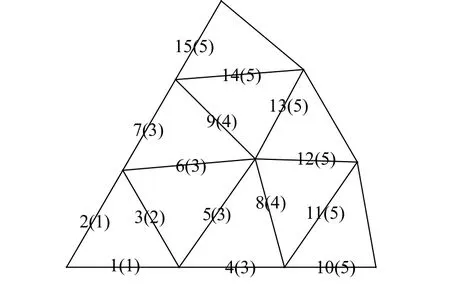
图3 K6N3单层球面网壳结构的杆件编号及分组(1/6模型)Fig.3 The component number and group of the K6N3 singlelayer reticulated shell (1/6 model)

该结构各杆件的冗余度值如图4所示，由此可知结构上部杆件的冗余度系数值较小，为结构的重要杆件；而结构下层杆件的冗余度系数值则相对较大，为结构的一般构件。

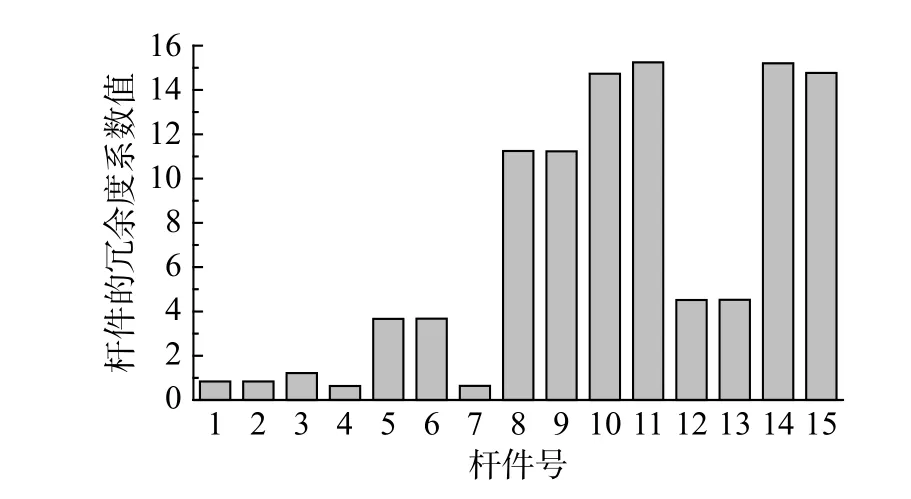
图4 优化前K6N3单层球面网壳结构各杆件冗余度系数Fig.4 The initial redundancy of K6N3 single-layer reticulated shell

结构各杆件移除后，结构的承载力下降量如图5所示，可以看出，低冗余度结构关键构件(杆件1、2、4、7)移除后引起的结构承载力变化量明显高于高冗余度结构杆件(杆件10、11、14、15)，说明本文采用的结构构件冗余度评价方法计算的构件冗余度能正确体现各构件的重要性。

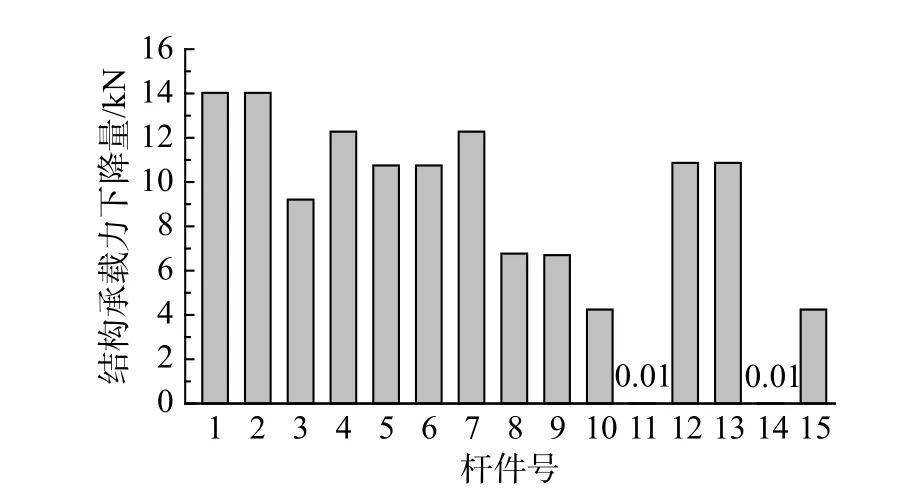
图5 K6N3单层网壳各杆件移除后的结构极限承载力下降量Fig.5 The reduction of structural ultimate bearing capacity after each structural members was removed

以最小化结构所有杆件的冗余度标准差与各层次杆件的冗余度标准差之和为目标函数，并考虑约束条件(结构杆件长细比、结构最大位移、材料用量等)，采用前述方法优化结构杆件的截面尺寸。优化中目标值的变化曲线如图6所示，当目标函数值达到22.44时杆件获得其最优的截面尺寸。优化前初始结构构件的冗余度偏差为26.40，与之相比优化后结构杆件的冗余度离散程度明显降低。在保持材料用量不变的前提下，优化得到的结构各杆件的截面参数如表1所示。此时结构杆件的最大长细比、按强度验算的最大应力和按稳定性验算的最大应力分别为145.08、90.20N/mm2和156.07 N/ mm2，均满足设计约束要求。

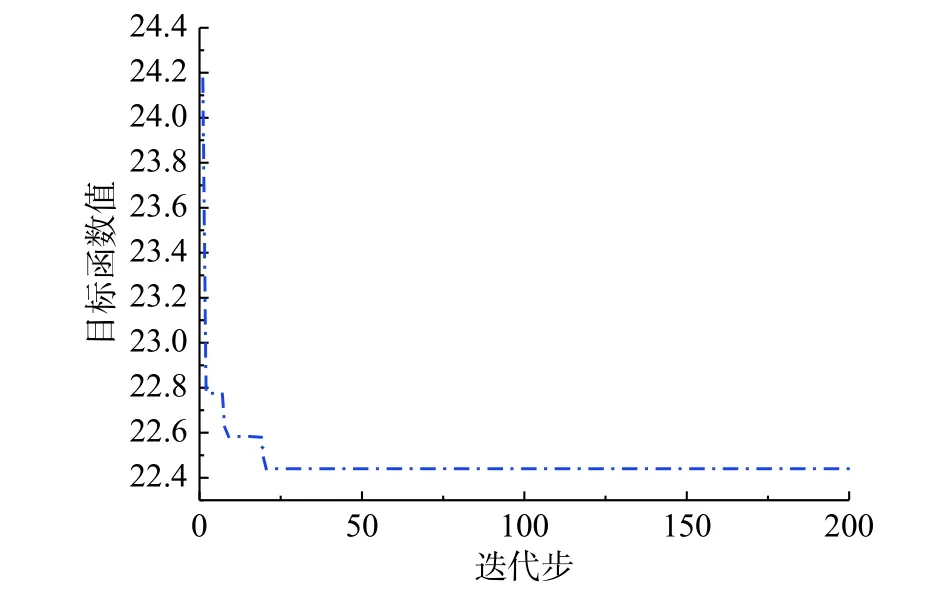
图6 优化中K6N3型单层网壳的目标函数值变化曲线Fig.6 The change curve of the value of objective function in the optimization of the K6N6 single-layer reticulated shell

表1 K6N3型单层网壳结构优化后的杆件尺寸Table1 The cross-sectional dimensions of the member in each group of the K6N6 single-layer reticulated shell after optimization

优化后，结构各杆件冗余度如图7所示，可以看出，结构杆件间的冗余度偏差明显减小。按《空间网格结构技术规程》(JGJ 7−2010)[14]的规定，对优化前后的结构施加L/300的初始几何缺陷进行结构极限承载能力分析，图8为该结构的加载过程与位移间的关系曲线。优化后结构极限承载力由原来的36.04 kN提高到40.33 kN，结构安全性有了明显提升。结果表明：通过优化结构杆件的截面尺寸，降低结构所有杆件的冗余度标准差与各层次杆件的冗余度标准差之和，可实现结构杆件间的冗余度偏差的减小，结构整体性能及其极限承载力得到显著提升。

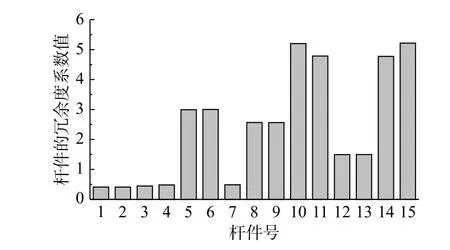
图7 K6N3型单层网壳结构优化后各杆件冗余度Fig.7 The redundancy of each member of the K6N3 singlelayer reticulated shell after optimization

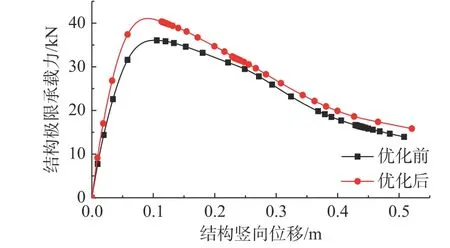
图8 K6N3型单层球面网壳结构荷载-位移曲线Fig.8 The load-displacement curve of the K6N3 single-layer reticulated shell

4.2 算例2：15 m跨单层柱面网壳结构

如图9所示一跨度、长度分别为1 5.0m和20.0m的柱面网壳结构，高跨比为1/5，长边周边节点设为固定支座，圆钢管构件，初始截面尺寸均为121.0mm×4.5mm ，材料弹性模量E为210.0 GPa，屈服强度fy为345.0 MPa，作用于结构上的等效节点荷载为10.0 kN，结构杆件编号及分组如图10所示。

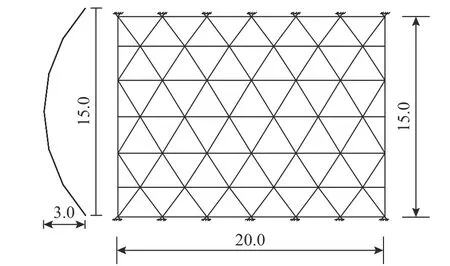
图9 一单层柱面网壳结构 /mFig.9 A single layer cylindrical reticulated shell

图10 柱面网壳的杆件分组(1/4模型)Fig.10 The component number and group of the cylindrical reticulated shell (1/4 model)

图11为该柱面网壳结构各杆件的冗余度值分布。可以看出结构纵向杆件的冗余度数值较大，而斜向杆件的冗余度则相对较小，总体上斜向杆件的重要性高于纵向杆件。

图11 柱面网壳结构优化前各杆件的冗余度系数Fig.11 The redundancy coefficient of each member of the cylindrical reticulated shell before optimization

将各杆件从结构中移除后的结构承载力变化量如图12所示，总体上冗余度系数值较低的斜向杆件移除后，结构承载力的下降幅度明显高于冗余度系数值较大的纵向杆件，说明结构杆件的冗余度值的大小可以反映该杆件在结构中的重要性及其破坏后对结构承载能力等性能的影响。

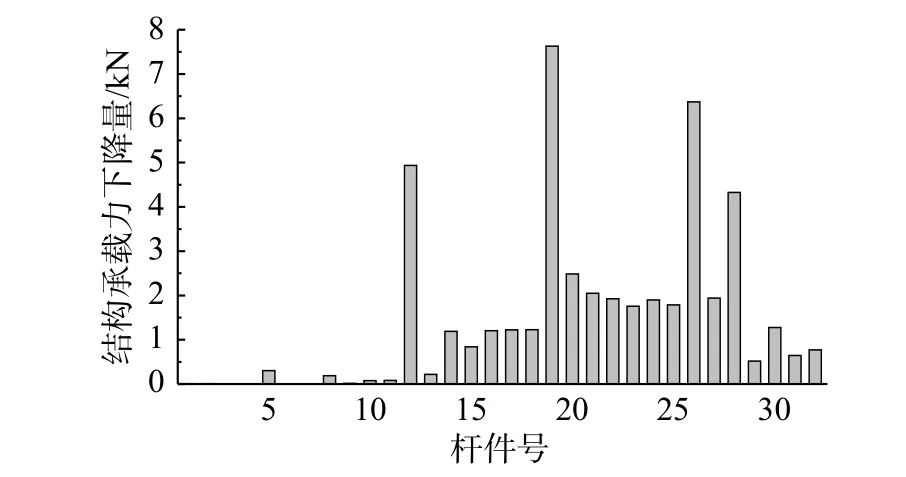
图12 柱面网壳各杆件移除后的结构极限承载力下降量Fig.12 The reduction of ultimate bearing capacity after each member of the cylindrical reticulated shell was removed

同理以式(12)定义的杆件冗余度标准差为目标函数，对结构各组杆件的截面尺寸进行优化，并考虑结构杆件的长细比、结构最大位移、材料用量等约束条件，其优化目标值随迭代步的变化曲线如图13所示，其目标函数值收敛于94.42。由式(12)得到初始结构的杆件冗余度偏差为114.65，与之相比优化后结构杆件的冗余度离散程度明显降低。在保持结构材料用量与原结构相同的条件下，优化后各组杆件的截面尺寸如表2所示。此时结构杆件的长细比最大值为78.79，按杆件强度验算的最大应力和按结构稳定性验算的最大应力分别为260.50 N/mm2和301.07 N/mm2，满足要求。

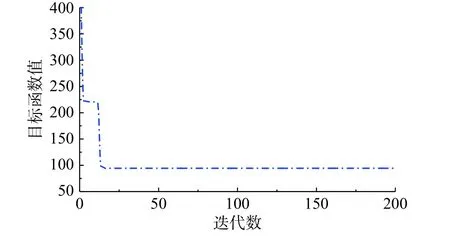
图13 优化中柱面网壳的目标函数值变化曲线Fig.13 The change curve of the value of objective function in the optimization of the cylindrical reticulated shell

表2 优化后单层柱面网壳各杆件的截面尺寸Table2 The cross-sectional dimensions of the member in each group of the cylindrical reticulated shell after optimization

优化后结构各杆件的冗余度如图14所示，由此可知结构纵向杆件的冗余度系数明显下降，而斜向杆的冗余度系数有所上升。图15为该结构的加载过程曲线。可以看出优化后结构极限承载力由46.43 kN提高至54.16 kN，结构性能得到了有效提升。同样说明通过优化结构杆件的截面尺寸，降低结构构件的重要性差异，可有效提升结构的整体性能及其承载力。

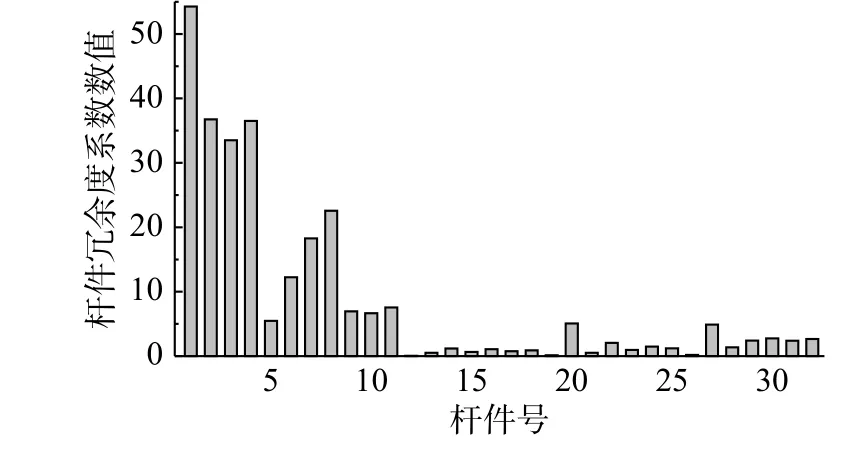
图14 优化后柱面网壳各杆件冗余度系数Fig.14 The redundancy coefficient of each member of the cylindrical reticulated shell after optimization

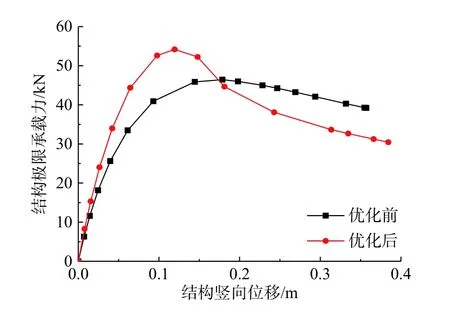
图15 柱面网壳结构的荷载-位移曲线Fig.15 The load-displacement curve of the cylindrical reticulated shell

5 结论

本文采用灵敏度分析方法定量分析了荷载作用下的构件的冗余度特性，以此衡量其在结构中的重要性。在此基础上，以结构所有构件的冗余度标准差与各层次构件的冗余度标准差之和最小化为目标函数，采用粒子群算法优化各构件的截面参数，平衡各构件在结构中的重要性，实现结构力学性能的提升。主要结论如下：

(1)本文采用的构件冗余度定量评估指标能有效地衡量和识别各构件在结构抗倒塌性能中的作用及其重要性，构件冗余度系数值可作为结构关键构件的判定参数。

(2)以降低结构所有构件的冗余度标准差与各层次构件的冗余度标准差之和为目标，基于粒子群算法通过优化各结构构件的截面参数，可实现结构构件重要性的均衡分布，结构极限承载力和整体性得到明显提升。