基于SWT的GIS电压互感器二次侧干扰分析

吴贤强，邹志杨，颜伟，周华良，刘兴发

(1.南京师范大学电气与自动化工程学院，江苏 南京 210046；2.南瑞集团有限公司，江苏 南京 211106；3.中国电力科学研究院有限公司武汉分院电网环境保护国家重点实验室，湖北 武汉 430000)

0 引言

与传统的空气绝缘变电站相比，气体绝缘变电站(gas insulated substation,GIS)占地面积小、运行安全、维护可靠，广泛应用于高压输电网络[1—2]。通常在开合隔离开关时母线上会产生特快速暂态过电压(very fast transient overvoltage,VFTO)[3—5]。VFTO一般分为内部VFTO和外部VFTO，前者对一次设备的绝缘设计提出了挑战[6—7]；后者通过辐射、传导、暂态壳体电压、地位升等方式对二次线缆及其所连接的二次设备造成影响，是影响变电站特别是变电站就地化保护装置电磁兼容性设计的关键因素[8]。

随着智能变电站的不断推进发展，二次设备逐渐集中，形成就地化保护装置[9]。采用就地化保护后，二次设备离骚扰源更近，面临的电磁干扰问题也更加严重，已发生多起由电磁干扰引发的电子式互感器故障[10]。目前对VFTO所引起的二次电缆和二次设备的电磁干扰问题建立了传导和辐射的模型[11—12]，但是对于此类二次侧电磁干扰的特性研究仍处于实测和仿真阶段[13]，对二次设备的电磁兼容测试没有明确的标准。因此有必要对二次侧干扰的频谱特性进行深入研究，在时频域范围内阐述二次侧干扰电压波形的特性。研究成果对二次侧干扰的数学计算模型建立、二次设备电磁兼容测试和电磁兼容防护设计具有重要意义。

VFTO波形具有非平稳特性，传统的傅里叶变换因无法反映频率分量随时间变化的特征而不再适用于求解 VFTO 的频谱[14]。文献[15]对几种时频变换的方法进行对比，最后采用广义S变换(generalized S transform,GST)得到了VFTO时频谱。由于二次设备所受到的电磁干扰是VFTO通过传导和辐射造成的，因此同样具有非平稳特性，但针对二次侧干扰的频谱分析研究目前仍停留在快速傅里叶变换(fast Fourier transform,FFT)和短时傅里叶变换(short-time Fourier transform,STFT)分析阶段[16]。目前缺乏性能更好、时频聚集性更强的时频分析方法来获得二次侧干扰准确的时频谱。

针对上述不足，文中采用同步压缩小波变换(synchronous compression wavelet transform,SWT)时频分析方法对1 000 kV GIS电压互感器(potential transformer,PT)二次侧干扰进行分析。首先采用自制的电磁瞬态测量系统对某1 000 kV GIS就地化保护装置PT二次侧端口上的共模骚扰电压进行了测量与分析。其次利用STFT、连续小波变换(continuous wavelet transform,CWT)、SWT、S变换(S transform,ST)和GST共5种时频分析方法分析合成的具有二次侧干扰特征的波形，并对比其性能。最后采用SWT分别对隔离开关合闸和分闸时的PT二次侧干扰进行时频分析。

1 PT二次侧干扰的测量

PT与GIS母线直接关联，VFTO主要通过传导方式对PT的二次侧产生共模干扰，PT二次侧的干扰通常是最为严重也是最有代表性的二次侧干扰。

文中自制一个专用的二次侧干扰电压测量系统，主要由衰减器、示波器、锂电池、逆变器、屏蔽箱、光纤通信系统组成。测量装置的具体构成如图1所示。锂电池和逆变器组成了示波器可靠稳定且无电磁干扰的供电电源。衰减器将输入干扰电压衰减了1 000倍，防止可能输入的高压对后端测量电路造成损坏。屏蔽箱的引入可以使测量系统免受一次设备所引发的辐射干扰，从而对PT二次侧干扰进行更为准确的测量。测量结果在屏蔽箱内进行光电转换，通过光纤传输到位于屏蔽室中的计算机上。测量系统中各组件的性能如表1所示。

图1 测量装置示意Fig. 1 Schematic diagram of measuring device

表1 测量系统中示波器和衰减器的性能参数Table 1 Performance parameters of oscilloscope and attenuator in measurement system

文中测量了隔离开关在开合空载母线时就地化保护装置PT二次侧输入的共模骚扰电压，包含PT二次侧的芯线对就地化保护装置的接地铜排的共模骚扰电压。共进行6次分合隔离开关测试，得到典型的测量波形如图2所示，其中H和M分别为宏脉冲群中最高幅值和较低幅值的微脉冲。文献[17]指出：一次开关操作全过程所产生的瞬态干扰以脉冲群的形式出现，称为宏脉冲，组成宏脉冲的独立脉冲称为微脉冲。对于测量结果中的工频分量文中不作讨论，只关注产生干扰脉冲的暂态过程。

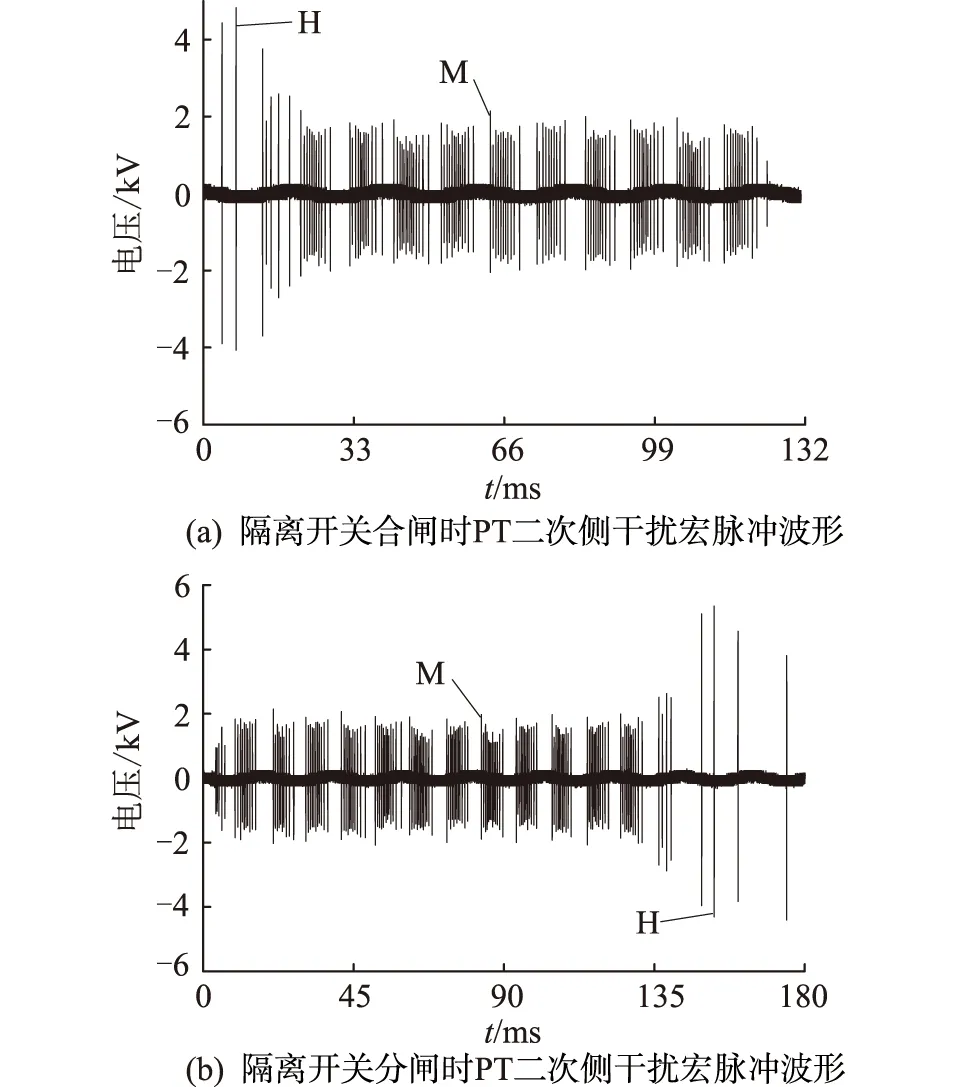
图2 隔离开关操作时PT二次侧干扰宏脉冲波形Fig.2 PT secondary side interference macro pulse waveforms during isolation switch operation

对隔离开关进行合闸操作和分闸操作时PT二次侧产生的宏脉冲分别如图2(a)和图2(b)所示。可以看出微脉冲间的时间间距不等，脉冲出现的最大频率约为1 kHz，整个干扰的持续时间约为120 ～170 ms，微脉冲峰峰值最高约为9.65 kV。对比图2(a)和图2(b)可知，随着隔离开关逐渐合闸，触头间隙逐渐减小，隔离开关触头间的击穿电压不断降低，微脉冲的峰峰值逐渐减小至0。对隔离开关进行分闸操作时，这种情况正好相反。

隔离开关操作时的PT二次侧干扰微脉冲波形如图3所示，微脉冲波形近似阻尼振荡波。图4为隔离开关操作时PT二次侧微脉冲FFT对比，可以看出，PT二次侧干扰脉冲幅值高并且频率分量丰富。频率分量主要处于1～100 MHz，文中测得的PT二次侧干扰主频为7.8 MHz。当隔离开关合闸开关间隙较大时，需要更高的击穿电压。此时对应的PT二次侧干扰首脉冲幅值最高，图4(a)对比傅里叶频谱可知幅值较高处微脉冲的频率分量相对于幅值较低处微脉冲的频率分量更为丰富。通过图4(b)对比合闸时PT二次侧干扰的傅里叶频谱可知,隔离开关分闸过程中触头间隙较大时产生的PT二次侧干扰幅值高，频率也更丰富。

图3 隔离开关操作时PT二次侧干扰微脉冲波形Fig.3 PT secondary side interference micro pulse waveforms during isolating switch operation

图4 隔离开关操作时PT二次侧微脉冲FFT对比Fig.4 Comparison of PT secondary side micro pulse FFT during isolation switch operation

2 SWT

由于FFT只能从整体上描述PT二次侧干扰电压波形所包含的频率成分，无法反映波形中各频率分量随时间变化的特性。因此需要采用对分析此类波形性能较好的时频分析方法提取二次侧干扰信号的时频特征，从时频域范围内揭示二次侧干扰的机理特性。

对于线性时频变换，受不确定性原理的约束,时间分辨率Δt和频率分辨率Δf是一对矛盾体[18]。其中任一分辨率的提高都会引起另一分辨率的下降。文中将STFT、CWT、ST、GST和SWT共5种时频分析算法就其分析二次侧干扰的性能情况进行了对比，选择其中性能较优的时频分析方法对二次侧干扰波形进行时频分析，期望得到更为准确的二次侧干扰时频谱。STFT、CWT、ST、GST等时频变换已经被广泛运用于很多领域[19—22]。具体算法原理可以参考文献[23]，文中不过多赘述。

SWT[24]以CWT为基础，压缩频率域上所有的频率成分，从而提高频率分辨率，消除交叉项，同时在尺度域上减少能量扩散，提高时频分布的聚集程度，更为清晰地显示时频分析结果。

对信号x(t)进行连续小波变换，定义为：

(1)

式中：a为尺度因子；b为时间平移因子。函数族φa,b(t)由基本小波函数φ(t)通过平移和伸缩产生。

(2)

利用小波变换得到的小波系数Wx(a,b;φ)，求取瞬时频率ωx(a,b)，可表示为：

(3)

上式可将时间-尺度平面转换到时间-频率平面(b,ωx(a,b))。此时可将任意频率ωl周围区间 [ωl-Δω/2,ωl+Δω/2]的值压缩到ωl上 ，提高时频分辨率，达到同步压缩变换的目的，同步压缩变换可表示为:

(4)

其中c为：

(5)

式中：ak为离散的尺度；k为尺度的个数。

3 时频分析方法性能对比

由于实测波形的频谱特征在频域和时域具有未知性，无法作为测试波形去判断时频分析算法的时频聚集性。文献[25]通过构造时频特性已知的波形作为测试波形来验证时频分析方法的性能。因此文中采用具有二次侧干扰波形特征的合成信号来测试上述几种时频分析算法的性能。

由图3可知，PT二次侧干扰信号是一个不断衰减的振荡波形，因此在构建具有该波形特征的合成信号时采用的是阻尼振荡波的数学模型。考虑到实际的PT二次侧干扰存在不同频率分量，合成信号采用多种频率的阻尼振荡波叠加。文中构造时间t从0 μs到5 μs的信号波形表达式为：

(6)

(7)

各频率分量的表达式以及存在的时间如式(6)、式(7)所示。合成信号的波形如图5(a)所示，波形的采样频率为200 MHz，总体上是一个衰减的振荡波形。其频谱如图5(b)所示，横坐标采用线性坐标，包含1 MHz，10 MHz，30 MHz，60 MHz和80 MHz共5个频率分量。

图5 PT二次侧干扰合成信号及频谱Fig.5 PT secondary side interference synthesis signal and spectrum

对合成的PT二次侧干扰信号采用上述5种时频分析算法进行分析，结果如图6所示。通过结果中的时频分辨率来判断各时频算法的性能。时频聚集性越强，越适合分析PT二次侧干扰。

图6(a)为STFT时频分析结果，由于STFT通过调节窗函数的宽度来调节时频分辨率，窗函数越宽时间分辨率越低，频率分辨率越高。文中通过调节窗函数的宽度，发现当海明窗取100时，时频分辨率效果最优，窗函数确定以后,只能以一种固定分辨率进行时频分析,无法兼顾高频信息和低频信息。

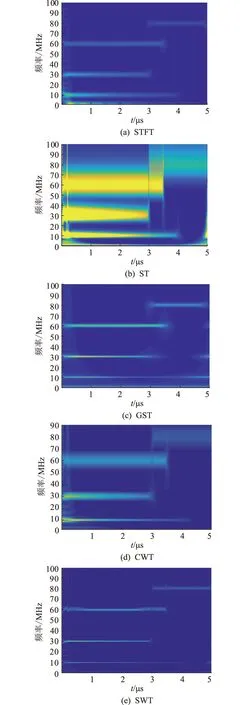
图6 5种时频变换方法得到的合成信号时频谱Fig.6 Time-frequency spectrum of synthetic signal ob-tained by five time-frequency transformation methods

图6(b)为ST时频分析结果，求解的频率对其时频分辨率影响很大。可以看出在低频段1 MHz和10 MHz时间分辨率和频率分辨率较高，越往高频处频率分辨率越低，时间分辨率越高。

图6(c)为GST时频分析结果，GST是基于ST提出的时频分析方法，通过调节因子λ对时频分辨率进行调节。对调节因子进行多次调试，发现调节因子为0.5时，所得到的结果较好。在低频段10 MHz调节因子的取值显得较大，导致其时间分辨率出现偏差，未能准确停止在4 μs处。在其他频段调节因子的取值较为合适，时频分辨率均较高。

图6(d)为CWT时频分析结果，选用Morlet小波作为母函数，从图中可以看出在低频段时间分辨率较低，频率分辨率较高，高频段的时频分辨率与低频段正好相反。

图6(e)为SWT时频分析结果。作为CWT的集成和发展，SWT具有更高的时频分辨率，并且在尺度域上可以减少能量扩散，提高时频分布的聚集程度。文中SWT选取bump小波作为母函数。低频段频率分辨率很高，时间分辨率略低。高频段时频分辨率均较高。从图6(d)、图6(e)可见，SWT、CWT均存在1 MHz处显示不清楚的缺陷。总体来说，对比以上时频分析的结果，SWT的时频聚集性明显高于STFT、CWT、ST和GST的时频聚集性。

4 实测波形的SWT分析

SWT可以压缩频率域上所有的频率成分，从而提高频率分辨率，消除交叉项，由上述分析结果可知SWT相对于其他所提到的时频变换方法具有更强的时频聚集性。采用SWT对隔离开关合闸分闸时宏脉冲中幅值最高的微脉冲波形进行时频分析，结果如图7所示。

图7 隔离开关操作时PT二次侧微脉冲的SWT分析结果Fig.7 SWT analysis results of PT secondary side micro-pulse during isolation switch operation

由图7可知隔离开关合闸和分闸时的PT二次侧干扰频率丰富，并且各频率分量的持续时间都不相同，说明VFTO引发的PT二次侧干扰确实具有非平稳特性。

图7(a)中隔离开关合闸时7.8 MHz频率分量持续时间贯穿波形的始终，是二次侧干扰的主导频率分量。其他频率分量例如20 MHz，25 MHz，30 MHz，65 MHz在波形发生后幅值就开始迅速衰减，持续时间不一，最长仅约为7.8 MHz频率分量持续时间的一半。7.8 MHz以下的低频段频率分量幅值较小，波形的持续时间约为2 μs。

图7(b)中隔离开关分闸时7.8 MHz频率分量依旧是主导频率分量。分闸时的频率分量主要集中在7.8 MHz，30 MHz，65 MHz，7.8 MHz以下的低频部分。

对比图7(a)和(b)可知，在进行隔离开关合闸操作时PT二次侧干扰频率更为丰富，并且在干扰发生的初期，非主频分量的幅值相较于分闸操作时PT二次侧干扰非主频分量的幅值更高。

5 结论

文中针对GIS中VFTO对二次设备和二次线缆的电磁干扰问题，对GIS的PT二次侧的干扰进行现场实测与分析，结论如下：

(1)文中测得的PT二次侧干扰脉冲最大频率约为1 kHz，整个干扰的持续时间约为120～170 ms。微脉冲峰峰值最高约为9.65 kV。单个微脉冲的频率分量丰富，主要处于1～100 MHz之间。微脉冲幅值越高，频率分量越丰富。

(2)对比不同时频分析方法的结果可知，SWT更能够准确反映各频率分量随时间变化的特性，适合分析VFTO所引发的PT二次侧干扰。

(3)SWT对文中测得的PT二次侧干扰的微脉冲进行时频分析的结果表明：7.8 MHz频率分量幅值高且贯穿波形的始终，是二次侧干扰的主导频率分量。其他频率分量在波形发生后幅值就开始迅速衰减，持续时间不一，最长仅约为7.8 MHz频率分量持续时间的一半。

本文得到南京市国际产业技术研发合作项目(201911021)，电网环境保护国家重点实验室开放基金项目(GYW51202001558)资助，谨此致谢！