NJ型扭矩传感器的改进

王晓阳 张昊 赵国华 蔡潜

摘要：本文主要介绍如何通过可靠的计算NJ型扭矩传感器的机械误差，来避免试验过程中校零操作，提高试验测量数据的精准度。

关键词：相位差;机械误差的最小二乘法;插值法;同心度误差

0.引言

NJ型扭矩传感器由于在制造过程中内外齿之间的机械误差是不可能完全避免的，齿与齿之间的机械误差更不能忽略，为了尽可能的减小生产制造中的机械误差对测量数据的影响，在每次试验进行前都必须零点校零。面对我们生产现场高电压、高转速的试验条件，进行零点校零是非常危险的，人为的增加了不安全隐患，也充分表现出了NJ型扭矩传感器的不足。为了避免试验校零操作，提高测量精准度，通过对NJ型扭矩传感器原理的研究，利用软件尽可能的计算出机械误差，这样就可以避免试验过程中的校零操作，提高试验效率及数据精准度。

1.NJ型扭矩传感器

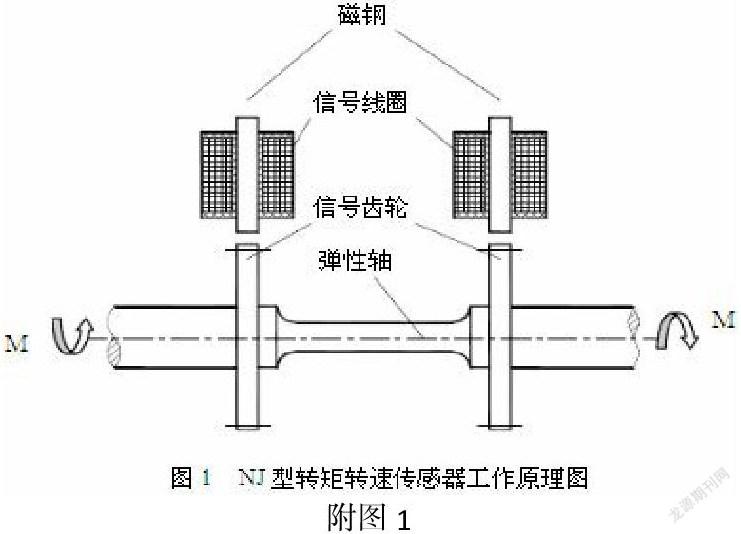
1.1NJ型扭矩传感器的工作原理

现在我们试验现场使用的都是NJ型扭矩传感器，因为在恶劣的环境条件下较其它类型的扭矩传感器NJ型扭矩传感器的抗干扰能力强，便于现场试验。

NJ型转矩传感器主要由弹性轴、磁电发生器、套筒及壳体等四部分组成。磁电发生器包括配对的两组内、外齿轮，磁钢和感应线圈。外齿轮安装在弹性轴测量段的两端;内齿轮在套筒内，和外齿轮相对，磁钢紧接内齿轮安装在套筒内。磁钢、内外齿轮构成环状闭合磁路，感应线圈固定在壳体的两端盖内。在驱动电机带动下，内齿轮随同套筒旋转。内外齿轮是变位齿轮，并不齿合，内外齿轮在相对旋转运动时，齿顶与齿槽交替相对，相对转动一个齿位时，磁路的磁通随之相应做周期变化，因此线圈中感应出近似正弦波的电压讯号，讯号电压瞬时值的变化和内外齿轮的相对位置的变化是一致的。

如果两组磁电发生器的齿轮的投影互相重合时、两组电压讯号的相位差为零。安装时，两只内齿轮的投影是重合的。而扭力轴上的两只外齿轮是按错动半个齿安装的。因此，两个电压讯号具有半个周期的相位差，即初始相位差为α0=180°。若齿轮为120°齿，分度角为3°，相位差为180°时，相应外齿轮错动1.5°。

当扭力轴受到扭矩作用时，产生扭角β，两只外齿轮的错位角变为1.5°±β两个电压讯号的相位差角应变为：α=120*（1.5°±β）=180°±120β.扭角和扭矩仪是成正比的，因此扭角的变化和扭矩成正比，即相位差角的变化为Δα=α-α0=±120β=120K1M=KM，式中K1为相位角和扭矩的比例系数，K=±120K1，”±”表示转动方向。

1.2NJ型扭矩传感器的不足

每次试验进行前都必须零点校零，在我们现场高电压、高转速的试验条件下进行零点校零是非常危险的，人为的增加了不安全隐患。而且扭矩校零时要尽量在接近实际测试的工况下，在实际测试的多个转速点上分别调零，以避免由于调零方法不对而带来转速特性误差、同心度误差，操作繁琐。

1.3NJ型扭矩传感器需要校零的原因

NJ型扭矩传感器输出两路电压波形，由于机械构造原因，此两路波形理论上有180度的相位差。但是齿轮、齿与齿之间的加工工艺和其它因素的影响，使扭矩传感器本身就存在不可避免的机械误差，内外齿相对齿间输出的波形相位差180度只能是理论上的，而且齿与齿间的误差也不可能一样，因此NJ型扭矩传感器在空载转动即零扭矩时，初始相位是在180°左右，每台传感器其初始相位都不一样，这样就造成了误差在一个周期内的叠加，所以在平常试验前都必须进行校零，拟合一条误差曲线，在测量过程中，扭矩测量仪自动将测量值减去对应点处的误差值即为我们所要的实际值。从这不难发现，我们平常所说的零点校零就是为了最大限度的降低生产制造中带来的机械误差。

2.对NJ型扭矩传感器进行改进的思路

NJ型扭矩传感器的机械误差就是指生产过程中内外齿相对齿间的相位误差，而且一个齿盘周期内不同齿间的误差也不一样，但是一个齿盘周期内所有齿间的误差总和是恒定的。由这可以发现，利用误差总和及最小二乘法原理求出均方根应该是我们所需的理想状态下的机械误差值，较曲线拟合出的机械误差值更精准。由此可见相位误差的测量是消除机械误差的关键，通过采集两路波形信号，分析两路波形的相位差角度，计算相位差的平均值得到初始状态下的机械误差。通过

T=K（α-α1）（α1为所测的机械误差对应的相位差角度）

通过计算得到所需的扭矩值。由于机械误差在一个周期内的叠加是恒定的，所以我们在带载试验前先减去机械误差，一方面省去了校零环节，方便使用和现场操作，另一方面使测量数据更精准。

3.基于Labview软件平台下扭矩、转速、功率的测量

3.1对α1机械误差的计算

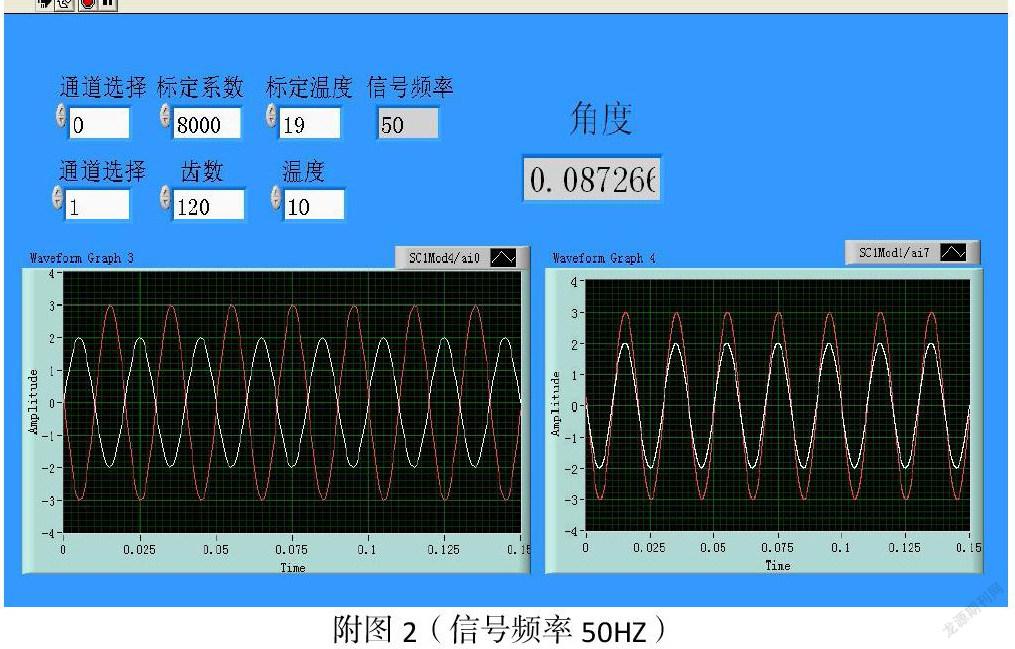
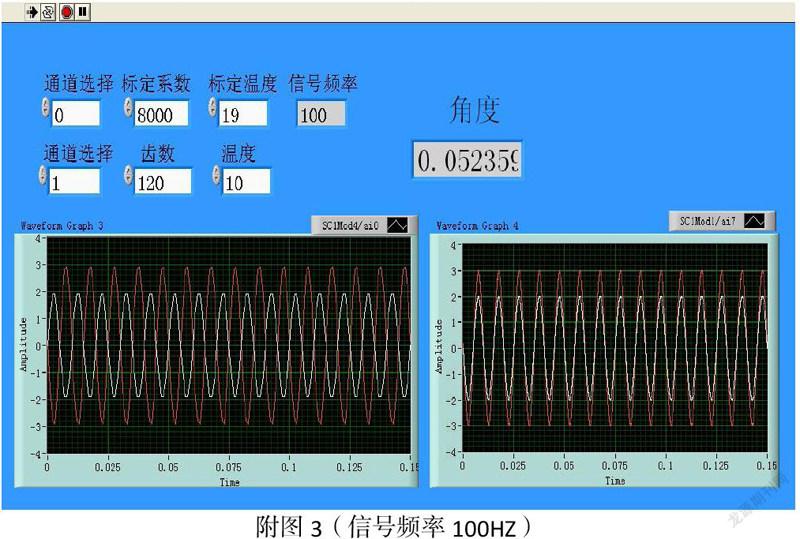
空载情況下采集扭矩传感器两路输出信号，通过功率因数COSα=P有功/P视在，利用反余弦函数计算出空载情况下的α1（注：由于机械误差是在齿轮一周上叠加的，所以尽量采集输出信号时采集齿轮一个周期的波形数据值求取均方根，如为120齿，最好采集120个周期数据），利用最小二乘法计算多个α1平均值，此时计算出来的α1为扭矩传感器的机械误差（所测的α1如图角度所示）。

注：⑴为了计算方便，将所采两波形中的其中一波形移相180°，如附图左波形图所示，移相后的波形如附图右波形图所示（附图2、3、4为采集信号不同频率下采集出的波形图及计算出的α1值）：

⑵由于采样率的限制，所采的波形在频率很高的情况下容易失真（如附图4中左波形图所示），为了更好的计算角度值，在程序设计中通过插值法拟合了正弦曲线（图中右为移相、插值后波形），使所采波形更接近于正弦波。程序如附图5所示：

3.2负载情况下的△α计算

负载情况下，根据同样方法计算出负载情况下的功率因数值，得到两路信号角度差α，由△α=α-α1得到负载时的相位差。

3.3扭矩比例系数K的计算

K1为传感器铭牌上的系数值，NJ型扭矩传感器通常为8000;

ΣG为传感器弹性轴的剪切弹性模量G的温度系数，由于现在生产的传感器的弹性轴材料均为40CrNiMoA，其ΣG均为-0.025%/℃;

t为测量时的环境温度;

t0为传感器标定系数时的环境温度。

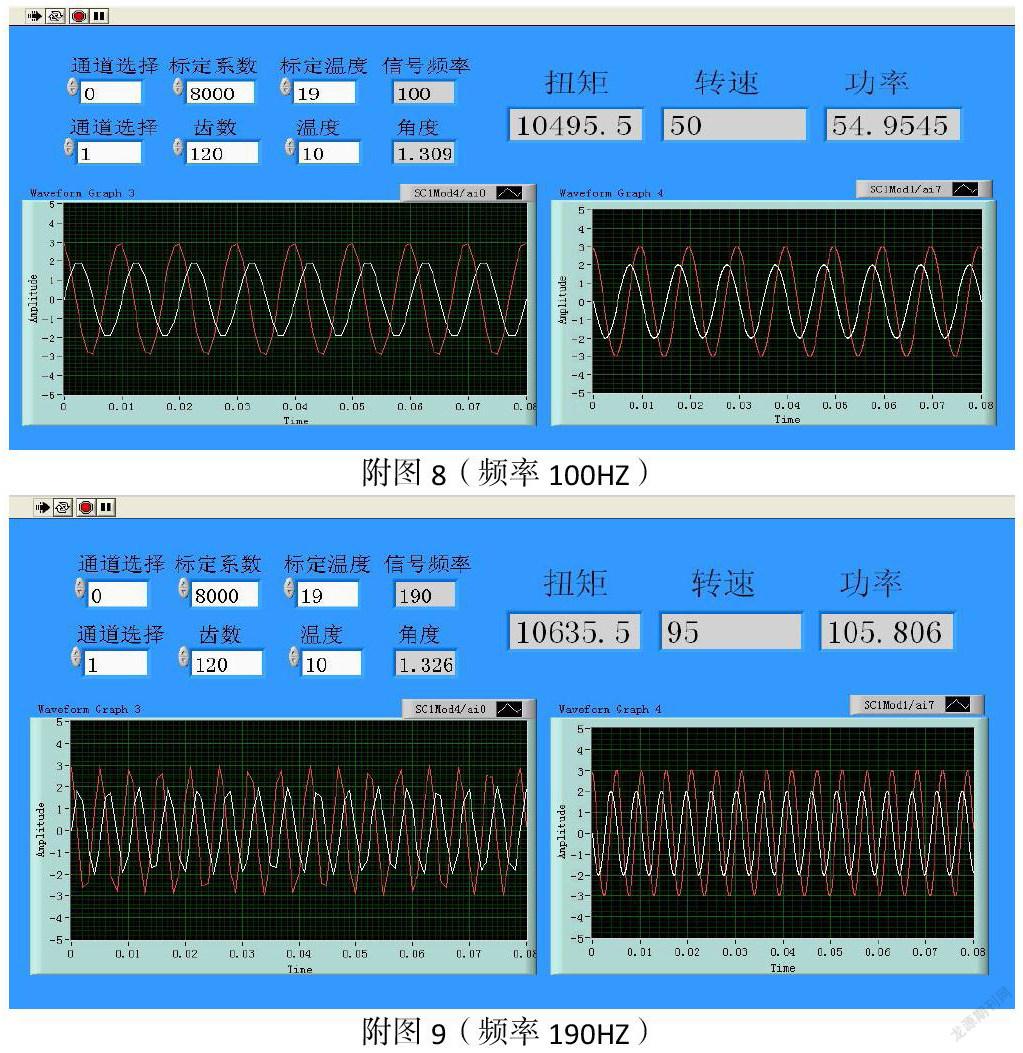
3.4带载情况下扭矩、转速、功率的计算

N=60f/n（f为所采信号的频率，n为齿数）

图形界面如附图所示（附图7、8、9为信号不同频率下的测量值）：

4.结束语

通过N=9550P/T验证所测的扭矩、转速、功率值及与扭矩测量仪所测数据对比可知，改进后所测的数据精准，可以很好的实现对扭矩、速度、功率的测量，更重要的是方便快捷准确，能更好地满足我们现场试验的需要。

参考文献

[1]《NJ型转矩转速传感器说明书》.四川诚邦测控技术有限公司.

[2]《误差分析与数据处理》.吴碄.清华大学出版社.2010.8.

[3]《电机学》.陈乔夫.华中科技大学出版社.2010.1.

[4]《数值分析》.李乃成.科学出版社.2011.9.

中车永济电机有限公司 山西永济 044502