煤层倾角对仰斜工作面覆岩压实区裂隙演化规律的影响

赵鹏翔，刘李东，李树刚,2，徐培耘，李 刚，魏宗勇,2，贾永勇

(1.西安科技大学 安全科学与工程学院，陕西 西安 710054；2.西安科技大学 西部矿井开采及灾害防治教育部重点试验室，陕西 西安 710054；3.新疆维吾尔自治区煤炭科学研究所，新疆 乌鲁木齐 830091)

0 引 言

我国煤层赋存条件差异大、整体透气性差，瓦斯直接抽采效果不佳，因此卸压瓦斯抽采显得十分重要[1-3]。而采动覆岩压实区对卸压瓦斯抽采系统的各项布置参数具有重要的影响，掌握其相关规律有助于提高抽采系统的瓦斯治理效果。目前，围绕采后岩层变化特征及其最终形态，李树刚等[4-6]通过物理相似模拟及数值模拟发现，煤层开采之后采动覆岩裂隙空间形态可以用椭抛带表征。伍永平等[7-9]、来兴平等[10-12]、罗生虎等[13-14]建立了大倾角煤层走向长壁开采岩体结构空间模型，对非对称煤岩的滑落失稳，进而诱发动力学灾害的机理进行了深入分析，并确定了维持大倾角工作面稳定性的区段煤柱合理尺寸。徐玉胜等[15]结合卸荷岩体力学与损伤力学分析研究了采高对采空区顶板卸荷及瓦斯通道演化的影响，得到了不同采高下瓦斯通道的卸荷损伤范围。刘洪永等[16]结合数值仿真对不同推进速度下的优势瓦斯通道的诱导与控制作用进行研究，建立了采动优势瓦斯通道带的时空形态理论模型。基于关键层理论，吴仁伦等[17]就工作面宽度对煤层群开采瓦斯卸压运移“三带”范围的影响进行了深入研究，提出不同的工作面宽度将极大地影响覆岩关键层的移动、破坏形态，进而进一步影响瓦斯卸压运移“三带”范围。张春雷等[18]结合UDEC数值模拟对近距离煤层群开采不同层间岩层结构下围岩裂隙演化规律进行了研究，发现亚关键层的层数、位置会影响覆岩裂隙的发育和分布，但不会影响裂隙的发展高度。7目前从上覆岩层的厚度[19-20]、强度[21-23]以及关键层层位[24]、工作面的采高[25-26]、推进速度[27]、推进距离[28]等方面对采动覆岩裂隙的演化规律及机理的研究较多，但煤层倾角这一对覆岩垮落形态及规律的重要影响因素开展研究较少。以山西和顺某高瓦斯煤矿主采工作面为试验原型，研究在不同煤层倾角条件下仰斜综采工作面覆岩裂隙网络压实区的演化规律，并结合采动覆岩裂隙椭抛带理论，构建考虑煤层倾角的采动覆岩裂隙演化模型，为仰斜综采工作面卸压瓦斯富集区精准探测提供一定的基础。

1 试 验

1.1 试验依据

试验以山西和顺某高瓦斯煤矿主采工作面为原型，开采水平为+1 150 m，平均埋深410 m，煤层平均厚度5.1 m，工作面采用走向长壁综合机械化一次采全高采煤法。直接顶为泥岩，局部含有砂质；基本顶为中砂岩。试验采用平面走向模型，煤岩层物理力学参数及上覆岩层高度见表1、表2。

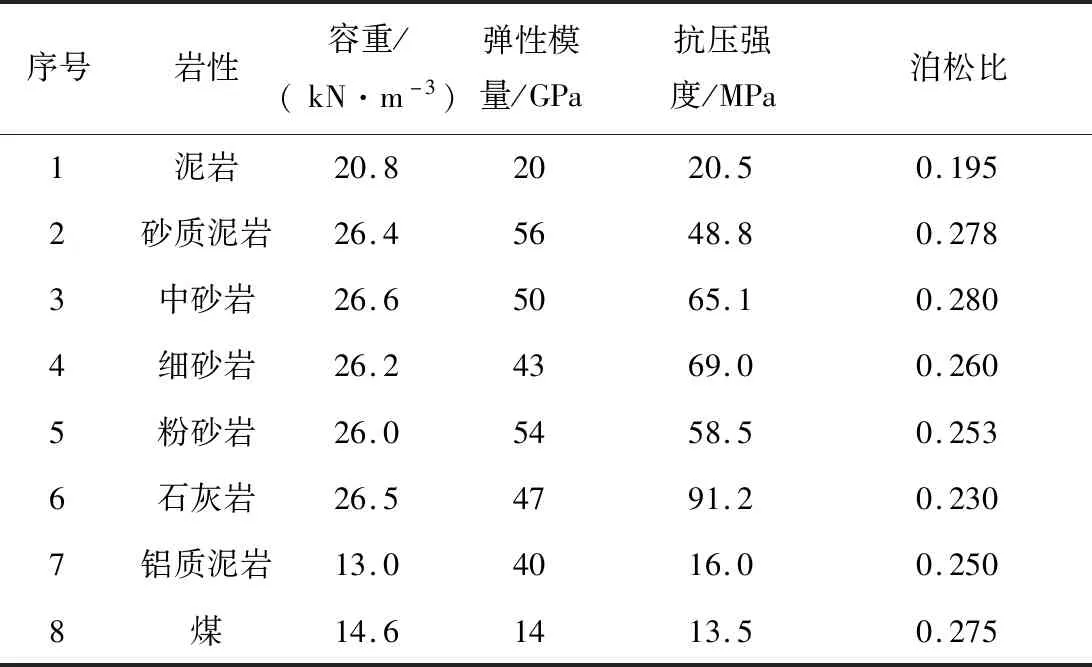
表1 煤岩层物理力学参数Table 1 Physical-mechanical parameters of coal and rock

表2 上覆岩层模拟高度Table 2 Simulation height of overlying strata

1.2 试验设计

试验利用自主研发的变化自角物理相似模拟试验台(图1)，搭建相似比例为1∶100的物理模型。首先，在试验台底部均匀铺设适宜的应力传感器，然后，按试验具体要求将模型搭建在其上方，待模型自然风干后，再布置相应的位移测点及顶部配重。根据物理相似模拟的特点，模型需满足几何、容重、应力、时间、强度以及泊松比相似的条件，见表3。

表3 模型相似常数Table 3 Similarity constant of model

图1 物理相似模拟试验模型Fig.1 Physically similar simulation test model

通过调整试验平台的角度(0°、15°、30°)，搭建3个只有倾角不同的试验模型。在模拟工作面推进时，两侧先各留宽10 cm煤柱，然后分别按2、3 cm依次循环推进的形式沿煤层走向方向仰斜回采。每次开采完成后，待岩层活动稳定之后拍照记录，并测量各位移测点的下沉量以及岩层的离层量。同时，通过预先埋设的应力传感器采集煤层底板应力。

2 试验结果

2.1 上覆岩层来压规律

工作面回采过程中，采空区上覆岩层内的原始应力遭到破坏，当工作面推进到一定距离时，高层位岩层逐渐产生弯曲断裂，加大了低水平岩层的竖向受力。同时下方悬臂梁随工作面的推进不断变长，导致下部岩层无法承受上部岩层的应力作用而产生周期性垮落，如图2所示。

图2 来压分布Fig.2 Distribution of periodic pressure

不同煤层倾角条件下周期来压显现时的推进距离不同，0°的平均来压步距为12.5 m，分别是15°以及30°的1.08、1.20倍。压实区是采空区上覆岩层受采动影响垮落堆积后，其中瓦斯渗透、运移明显更困难的局部区域，一般在1～2次周期来压后初步形成。煤层倾角越大，周期来压到来所需推进距离越短，因此，压实区的发育周期不断变短，为之后的缓慢充分的发育提供了更为充足的时间。

2.2 覆岩离层量分布规律

覆岩离层量即相邻岩层间的裂隙宽度，是定量描述采动过程中覆岩离层的动态变化的重要指标。覆岩离层量分布如图3所示，在受采动影响的采空区边缘，覆岩的离层量较大，而采空区中部因高层位的岩层破断及垮落，挤压低层位的岩层，迫使离层裂隙压缩变窄，甚至闭合，从而离层量较小。根据文献[6]中对压实区的判定准则，即压实区采动覆岩离层量相对于两侧边界较小且在采空区底板会形成应力集中现象，两者结合可判定压实区边界。因此，结合图3，可大致判定中部的压实区和边界的裂隙区所在区域。

图3 覆岩离层量分布Fig.3 Abscission layer distribution of rock

由于裂隙区的离层量普遍大于压实区，故在二者交界区域离层量的大小会有较明显的变化。随着煤层倾角的增加，中部压实区和两侧裂隙区所对应的离层量也逐渐增加，但受岩层自身硬度、厚度以及层位的影响，最大离层量的增加值在减小。而在压实区中，受采动影响后不同层位的岩层垮落形成的堆砌状态以及所受到的外力大小及方向都存在一定差别，因此，压实区覆岩离层量的数值会有一定的波动。

2.3 工作面底板应力分布特征

通过分析模型底板处应力传感器监测到的回采期间的应力数据，如图4所示，发现采空区底板的应力相较于回采前明显变小，且应力集中系数在0.05～0.45波动。由于中部的压实区直接受到上位岩层向下的重力，而两侧的裂隙区得益于垮落时形成的铰接结构的支撑作用，中部的压实区应力集中系数要比两侧裂隙区的大一些，在3个区域的交界处，其应力集中系数会有较为明显的变化，如图4中的局部放大的区域所示。同时，结合覆岩离层量的分布规律可知，不同煤层倾角压实区的宽度扩展5～7 m。

图4 工作面底板应力分布Fig.4 Stresses distribution of bottom plater

2.4 压实区的空间演化规律

根据文献[6]中对压实区的判定准则，再结合模拟试验中周期来压具体时段、覆岩裂隙发育情况、以及底板应力分布规律，绘制不同煤层倾角的压实区演化形态(图5)。

图5 不同煤层倾角压实区演化形态Fig.5 Different mining angle of evolution form of compacted area

由图5可知，随着回采工作面的不断推进，压实区也不断的扩展。周期来压依次显现时，压实区明显在沿工作面方向扩展，同时也在向更高层位发展。在压实区向更高层位发展时，覆岩会形成一定的垮落角，且垮落角在逐渐地减小，使得压实区的左右边界呈椭圆抛物线状。不同煤层倾角条件下所表现出的压实区形态有着明显的差异，主要体现在高度、垮落角以及宽度这3个方面。

3 讨 论

3.1 压实区高度的倾角效应分析

如图6所示，压实区的高度随着工作面的推进持续增大，同一推进距离下，煤层倾角越大，压实区的高度越高。压实区高度拟合直线斜率初期较小，这是由于压实区在形成初期，受采动影响的覆岩范围较小，压实区整体规模相差不大，即不同煤层倾角下的压实区的高度在采煤初期差值不大。当工作面推进至一定距离时(55～65 m)，拟合直线斜率剧增，如图6中阴影区域所示，这是由于受煤层倾角影响，平均来压步距减小，煤层倾角较大的工作面发生周期来压的次数更多，压实区发育更为充分，导致其高度明显增大。当工作面推进距离达到80 m后，斜率又趋于稳定，不同煤层倾角下的压实区的高度其差变化不再明显，受推进距离的影响减小。

图6 不同煤层倾角压实区高度拟合直线斜率变化趋势Fig.6 Change trend of height slope in compacted zone of different coal seam inclination angle

由于压实区的高度受到工作面推进距离和煤层倾角的共同影响，为了能定量化描述压实区高度与煤层倾角及工作面推进距离之间的关系，将三者进行多元拟合，得到拟合关系：

H=25.812ln(L-10.057)+0.178θ-69.216，R2=0.949

(1)

式中：H为压实区高度，m；L为工作面推进距离，m；θ为煤层倾角，(°);R2为决定系数。

3.2 压实区垮落角的倾角效应分析

如图7所示，随着煤层倾角的增大，开切眼侧垮落角α逐渐减小，工作面侧垮落角β逐渐增大，但随工作面推进距离的增加，两侧垮落角都在逐渐减小。煤层倾角越大，下滑作用越强，受采动影响的上覆岩层破断及垮落后沿煤层底板向下滑动或滚落填充下部采空区，且煤层倾角越大，填充下部采空区的岩块堆砌的高度越高，导致开切眼侧的上覆岩层垮落空间相对减少，并且受到下部填充岩块的支撑，使得岩层间形成较大的离层却未发生垮落，而以覆岩离层量为判定依据的开切眼侧压实区边界则向工作面侧进一步弯曲倾斜。因此，对于开切眼侧的垮落角α而言，煤层倾角越大，其值越小。

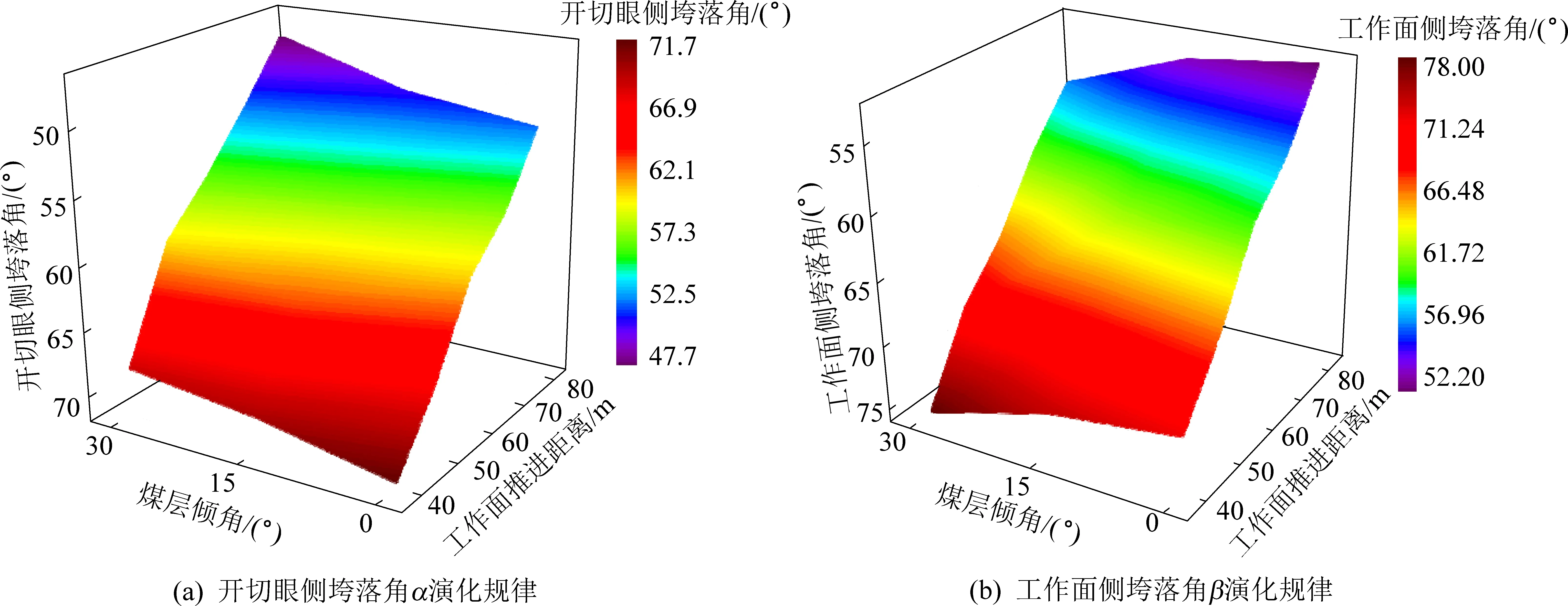
图7 不同煤层倾角压实区垮落角演化规律Fig.7 Different of mining angle of evolution of collapse angle

煤层倾角越大，下滑作用越强，岩块堆砌的速度越快，导致填充下部采空区的岩块在滑动或滚落的过程中相互摩擦、碰撞及挤压程度加剧，岩块的单个体积更小，单位空间内堆砌的岩块更多，进而进一步增大了工作面侧上覆岩层的垮落空间，难以得到下部垮落岩块的支撑，使其不易形成较大的离层量，从而工作面侧的压实区边界向开切眼侧的弯曲倾斜程度相对减小。因此，对于工作面侧的垮落角β而言，煤层倾角越大，其值越大。

由于压实区的垮落角受到工作面推进距离和煤层倾角的共同影响，为了能定量化描述压实区垮落角与煤层倾角及工作面推进距离之间的关系，将三者进行多元拟合，得到拟合关系：

α=-0.640lnL-0.003θ+3.576，R2=0.981

(2)

β=-0.711lnL+0.008θ+3.878，R2=0.960

(3)

3.3 压实区宽度的倾角效应分析

由于压实区的垮落角是逐渐减小的，这使得压实区的边界存在一定的弧度，但同时受到下滑作用的影响，从而左右边界呈不对称椭抛线状。而压实区形成之后，其扩展的部分都是在前一次的基础上进一步形成的，因此根据式(2)和式(3)所得到的垮落角拟合公式，可以建立如图8所示的简化模型。

图8 走向压实区简化模型Fig.8 Simplified model of compacted area

进一步得到压实区宽度与垮落角及垮落高度之间的关系。由于中部压实区边界呈不对称椭抛线状，近似认为该模型是由2部分组成的，可得到以下关系：

Li=Lαi+Lβi

(4)

Lαi=ΔHα1cotα1+ΔHα2cotα2+…+
ΔHαncotαn=Hα1cotα1+(Hα2-Hα1)×
cotα2+…+(Hαn-Hαn-1)cotαn=

(5)

则：

(6)

式中：Li为第i次形成的压实区宽度，m；Lαi为第i次形成的压实区开切眼侧的宽度，m；Lβi为第i次形成的压实区工作面侧的宽度，m；ΔHαi为第i次压实区扩展时开切眼侧高度的增量，m；Hαi为压实区第i次扩展时开切眼侧的高度，m;Hβi为压实区第i次扩展时工作面侧的高度，m;αi为压实区第i次扩展时开切眼侧形成的垮落角，(°)；βi为压实区第i次扩展时工作面侧形成的垮落角，(°)。

根据所得的压实区高度、垮落角与工作面推进距离和煤层倾角的关系，将其代入式(4)中，便可得到压实区宽度与工作面推进距离和煤层倾角的关系。

4 采动裂隙椭抛带压实区演化倾角效应模型

通过物理相似模拟试验可以发现，采空区中部的压实区受下滑作用影响而整体呈不对称的类椭圆抛物面。根据试验所得数据，将压实区倾角模型旋转θ(θ为煤层倾角)建立了如图9所示的椭抛带压实区演化模型，同时，基于采动裂隙椭抛带理论，结合式(1)—式(6)，构建了受煤层倾角及工作面推进距离共同影响的压实区空间形态数学表征方程。

图9 采动裂隙椭抛带压实区空间几何模型Fig.9 Geometric model of compacted area in elliptic paraboloid zone

(7)

式中：x1、y1、z1为图9中压实区的坐标值；A1、A2分别为进、回风巷处，压实区底部边界与其距离，m；Lk为工作面宽度，m；La为压实区底部边界至开切眼处的距离，m；Kc为压实区范围内岩层破断碎胀系数；H为压实区高度，m。

5 结 论

1)随着煤层倾角的增大，相同区域内的采动覆岩离层量随之增大，结合覆岩离层量与底板应力分布规律，可知不同煤层倾角下压实区的宽度扩展5～7 m。

2)随着煤层倾角的增大，平均来压步距逐渐减小(12.5 m>11.6 m>10.4 m)，工作面推进至55～65 m时，煤层倾角较大的工作面发生周期来压次数更多，压实区之间的高差急剧增大。

3)同一推进距离下，煤层倾角越大，压实区工作面侧垮落角越大，开切眼侧垮落角越小，结合压实区高度演化规律，建立受煤层倾角因素影响的走向压实区简化模型，对压实区宽度分段表示。

4)建立了考虑煤层倾角因素的采动裂隙椭抛带压实区数学方程，为进一步研究受煤层倾角因素影响的采动覆岩裂隙发育规律，准确定位仰斜综采工作面卸压瓦斯富集区提供一定的理论依据。