滚动轴承的振动性能退化过程与保持可靠性研究

程 立, 夏新涛,2, 马文锁,2

(1. 河南科技大学 机电工程学院, 河南 洛阳 471003;2. 河南科技大学 机械装备先进制造河南省协同创新中心, 河南 洛阳 471003)

1 引 言

滚动轴承在机械设备上有着广泛应用,一旦出现故障会造成巨大的经济损失和严重的人员伤亡[1,2],这使得滚动轴承的可靠性[3～6]成为了一个热门的研究领域。大量的关于滚动轴承可靠性的研究是建立在概率分布与趋势均已知的经典统计学基础上[7,8],并根据失效数据来构建寿命可靠性预报模型。但是这类方法的缺陷在于难以解决事先概率分布与趋势未知的可靠性预报问题[9,10]。针对上述问题,夏新涛等[11]根据滚动轴承的振动性能数据建立了滚动轴承的性能保持可靠性评估模型。滚动轴承的性能退化描述的是滚动轴承的运转性能从正常到失效的过程,精准的评估滚动轴承的退化历程能够避免意外停机造成的经济损失。传统的方法主要从时域、频域以及时频域方面进行研究,近年来人工智能、混沌理论、熵理论[12]在滚动轴承退化研究上得到广泛的应用。王冰等[13]针对轴承性能退化状态的识别问题,提出一种基于基本尺度熵与GG(gath-geva)聚类的退化状态识别方法。许迪等[14]提出基于流形学习和M-KH-SVR(multivariable-krill herd-support vector regression)的滚动轴承衰退预测方法。姜万录等[15]出了一种基于变分模态分解(VMD)和支持向量数据描述(SVDD)相结合的滚动轴承性能退化程度定量评估方法。以上的文献均是对滚动轴承性能退化进行研究,但是关于滚动轴承的性能退化历程和可靠性之间存在怎样的关系研究较少。

本文对滚动轴承的性能退化过程与其保持可靠性之间的关系进行研究。首先基于最大熵法和泊松过程[16]建立滚动轴承振动性能保持可靠性模型,然后提出一种基于最大熵法[17]和相似度法[18～20]的滚动轴承性能退化模型。最后基于灰关系理论[21]对滚动轴承的性能退化序列和保持可靠性序列之间的关系进行评估。

2 模型描述

在滚动轴承服役期间,对其振动信号进行定期采样。定义时间变量为t,数据采样时间周期为ω,ω为取值很小的常数,滚动轴承服役周期内可获得r个振动序列。本征序列是指滚动轴承最佳运行状态时期的振动序列,记为第1个振动序列,用向量X1表示。

X1=[x(1),x(2),…,x(N)]

(1)

式中N为振动数据的总个数。

随着时间t进行,不断采集振动数据,获得第n个振动序列Xn:

Xn={xn(1),xn(2),…,xn(N)}

(2)

式中n为振动序列的序号,n=1,2,…,r。

所获得的振动序列矩阵X可以表示为:

X=[X1,X2,…,Xr]

(3)

2.1 滚动轴承振动性能保持可靠性模型

2.1.1 最大熵原理

运用最大熵原理[17]能够对未知的概率分布做出主观偏见为最小的最佳估计。为叙述方便,用连续变量x表示本征序列中的离散变量。

根据最大熵原理,最无主观偏见的概率密度函数应满足熵最大,即

(4)

式中:H(x)为信息熵;Ω为随机变量x的可行域;f(x)为连续变量x的概率密度函数。

式(4)应满足约束条件:

(5)

(6)

式中:i为原点距阶数,i=0,1,2,…,m;m为最高阶原点距的阶次;mi为第i阶原点距,m0=1。

采用拉格朗日乘子法求解此问题,通过调整f(x)使熵达到最大值。设L(x)为拉格朗日函数,ci为第i个拉格朗日乘子,从而得到:

(7)

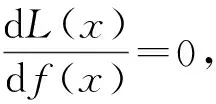
(8)

因此,可得概率密度函数f(x)的表达式为:

(9)

根据式(5)和式(9),可得:

(10)

(11)

将式(10)对ci进行微分,可得:

(12)

将式(11)对ci进行微分,可得:

(13)

根据式(12)和式(13),可得其它的拉格朗日乘子应满足条件:

(14)

通过式(14)可得到求解ci;再根据式(11)可求解出c0,进而根据式(9)求解出f(x)。

2.1.2 本征序列振动数据的参数估计

本征序列振动数据的估计真值X01为:

(15)

设显著水平α∈[0,1],则置信水平为:

P=(1-α)×100%

(16)

(17)

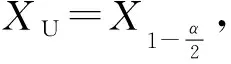
(18)

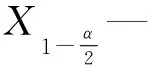
因此,连续变量x的最大熵估计区间为:

(19)

计算本征序列的最大熵估计区间[XL1,XU1],其中,XL1为本征序列最大熵估计区间的下限值,XU1为本征序列最大熵估计区间的上限值。

2.1.3 基于泊松计数原理求振动性能保持可靠度

记录第n个振动序列的振动数据落在本征序列最大熵估计区间[XL1,XU1]之外的个数Nn,获得第n个振动序列的变异频率θn,表示为:

(20)

滚动轴承性能保持可靠度R(n)用于表征滚动轴承运行可以保持最佳振动性能状态的可能性[16]:

R(n)=exp(-θn)

(21)

2.2 滚动轴承的振动性能退化模型

对于滚动轴承的第n个振动性能数据序列Xn

Xn={xn(1),xn(2),…,xn(N)}

(22)

先对Xn进行归一化处理,然后进行等概率可放回的多次抽样,可得到一个自助样本Yb,设为

Yb={yb(1),yb(2),…,yb(k),…,yb(j)}

(23)

其中:j为自助样本数据序列总个数;yb(k)为自助样本的第k个数据。

则自助样本的均值为:

(24)

按此方法重复进行B次,从而得到一个样本含量为B的自助样本,可表示为:

YB={Y1j,Y2j,…,Ybj,…,YBj}

(25)

式中b=1,2,…,B。

对自助样本YB运用最大熵方法,求取概率密度函数。设滚动轴承本征序列自助样本的最大熵概率密度函数为:

(26)

设滚动轴承其它序列自助样本的最大熵概率密度函数为:

(27)

定义退化概率为:

(28)

式中Θ为随机变量x的可行域,即f1(x)与fn(x)的重叠部分。

当退化概率Q的值很小时,滚动轴承的振动性能发生退化的可能性很低,即滚动轴承维持在良好的运转性能中;当退化概率Q的值变大时,滚动轴承的振动性能发生退化的可能性变高,即运转状况变恶劣。

2.3 振动性能保持可靠性与退化概率的灰关系评估

根据式(21),可求得性能保持可靠度序列Φ1:

Φ1={φ1(1),φ1(2),…,φ1(n),…,φ1(r)}

(29)

式中φ1(n)=R(n)。

同样,根据式(28),可以求出退化概率序列Φ2:

Φ2={φ2(1),φ2(2),…,φ2(n),…,φ2(r)}

(30)

式中φ2(n)=Q(n)。

对性能保持可靠度序列Φ1和退化概率序列Φ2进行归一化处理,然后分析其关联程度。

式(29)和式(30)中,Φ1和Φ2的样本分别为φ1(n)和φ2(n),设:

(31)

(32)

式中l=1,2。归一化处理得：

(33)

则有

Gl={gl(n)}

(34)

式中Gl为Φl的规范化生成序列。

对于归一化生成序列Gl,有gl(n)∈[0,1],gl(1)=0,gl(r)=1。

在最少量信息原理下,对于任意的n,若Gl是规范化排序序列,则参考序列GΛ的元素可以是常数0,即gΛ(1)=gΛ(2)=…=gΛ(n)=…=gΛ(r)=0。

取分辨系数ε∈[0,1],可以得到灰关联系数的表达式:

(35)

式中ΔΛl(n)为灰差异信息,可表示为:

ΔΛl(n)=|gl(n)-gΛ(n)|

(36)

定义灰关联度为

(37)

定义两个排序序列Φ1和Φ2之间的灰差为

d1,2=|γΛ1-γΛ2|

(38)

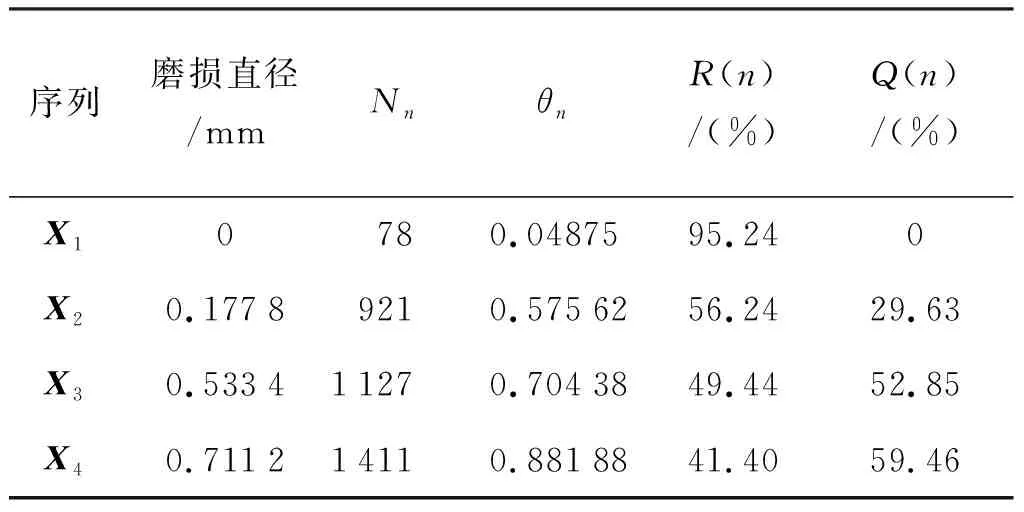
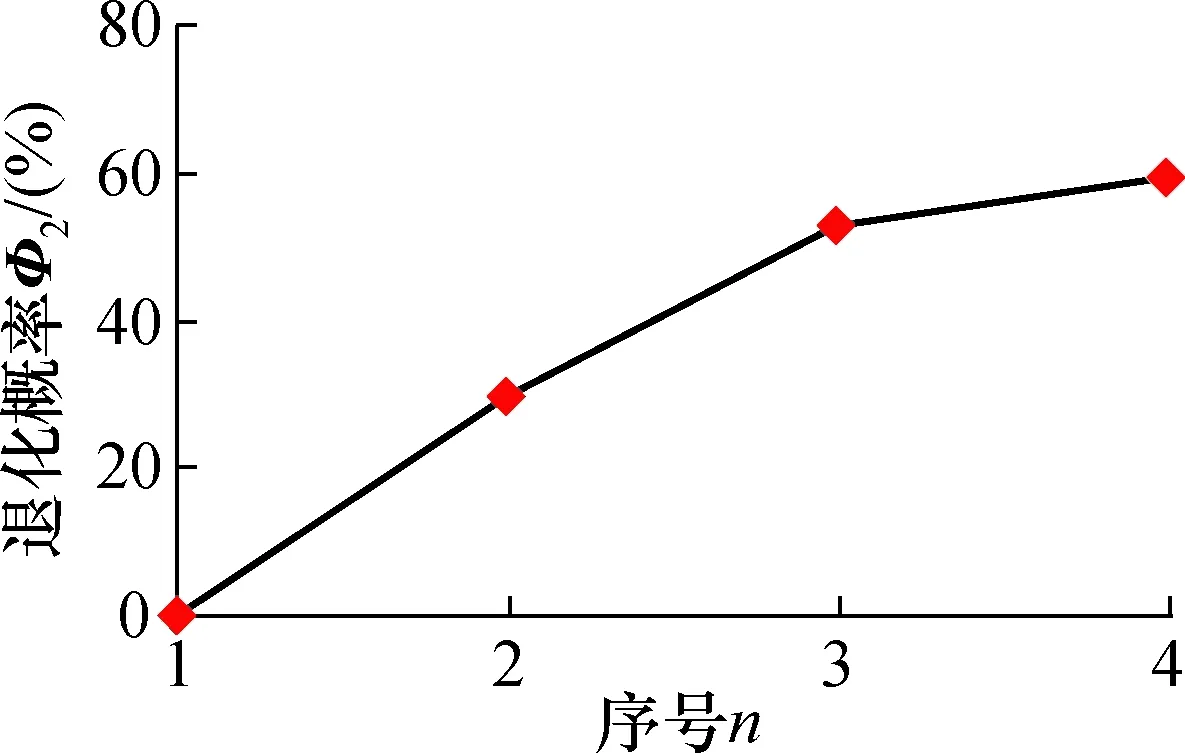
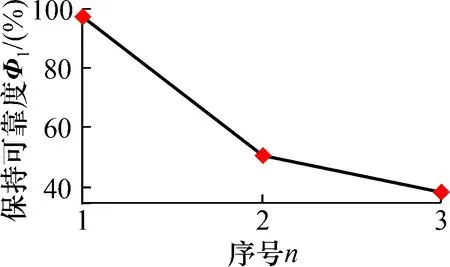
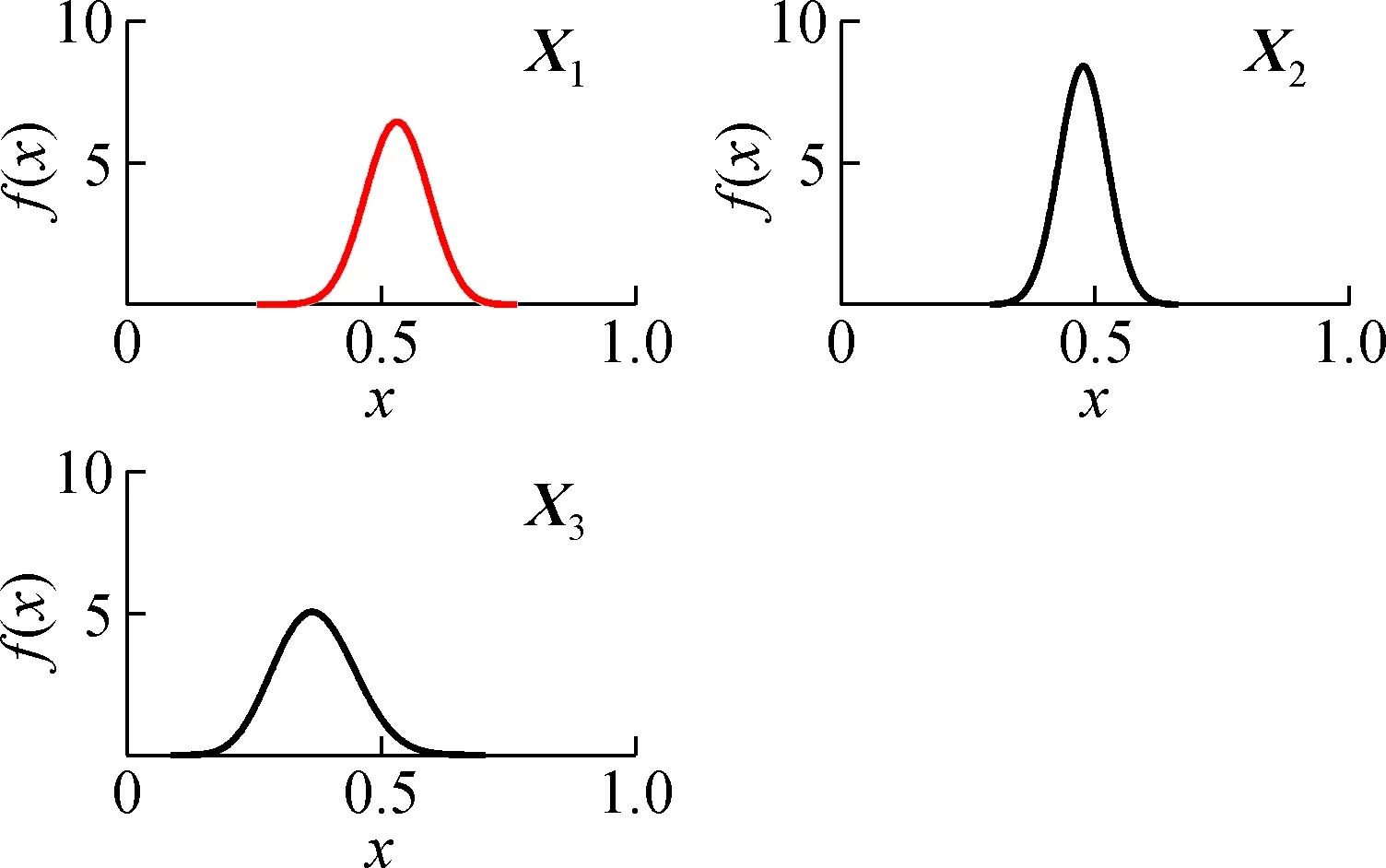
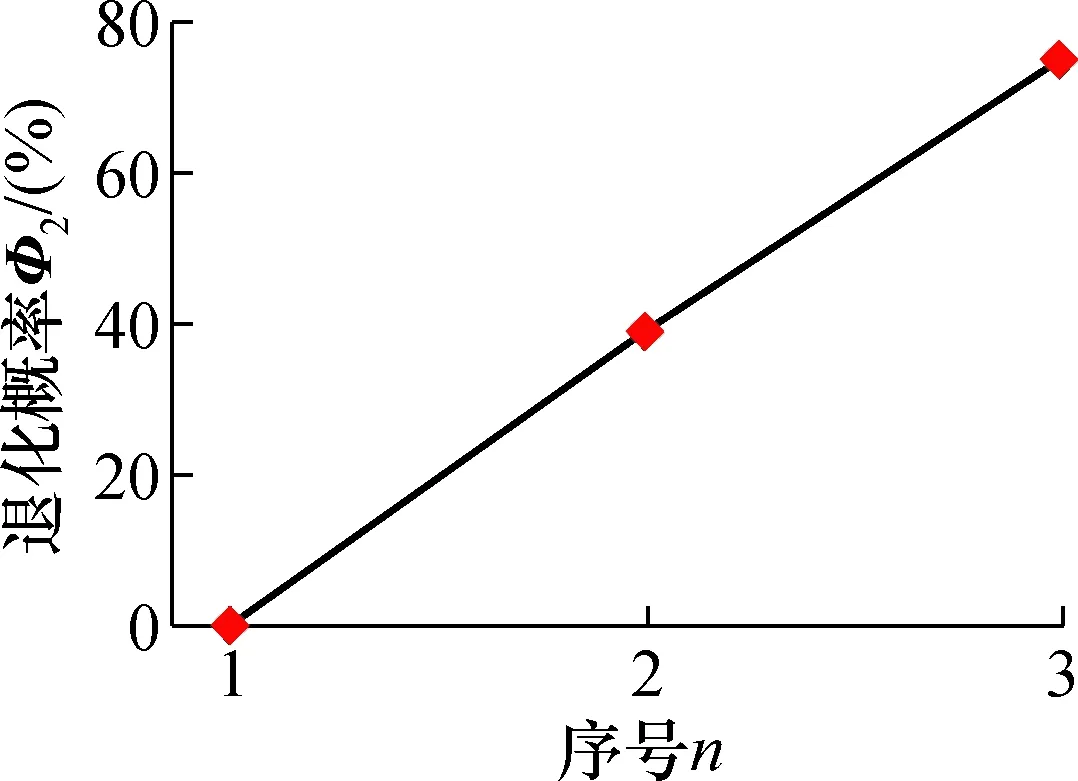
给定Φ1和Φ2,对于ε∈(0,1],总存在唯一的一个实数dmax=d1,2max,使得d1,2

定义基于2个数据序列Φ1和Φ2之间灰关系的属性权重为

(39)

式中:属性权重f1,2∈[0,1];参数η∈[0,1]。

根据灰色系统理论[21],在给定准则下,默认λ为真元的代表。对于式(39),给定Φ1和Φ2,取参数λ∈[0,1]为水平,若存在一个映射f1,2≥λ,则认为Φ1和Φ2具有相同的属性,λ为模糊数。当λ=0.5时,研究对象的两实体模糊性达到最大,介于较难分辨的真和假之间;当λ﹥0.5时,Φ1和Φ2灰关系趋于清晰;当λ﹤0.5时,两事物关联度较小或者两者之间差异大,所以,取f1,2=λ=0.5,认为轴承振动性能保持可靠性Φ1和振动性能退化概率Φ2具有相同的属性。

设η∈[0,0.5],由式(39)可得dmax=(1-f1,2)η。令

P1,2=1-(1-λ)η=(1-0.5η)×100%

(40)

式中:P1,2为灰置信水平,又称为灰理论概率;P1,2描述了Φ1和Φ2属性相同的可信度;η值可由式(40)求得。灰置信水平取值越大,滚动轴承振动性能保持可靠性Φ1和振动性能退化概率Φ2之间的关系越密切;反之,两者之间的关系越疏松。这表明了轴承振动性能保持可靠性和振动性能退化概率之间的本质关系。具体实施时,可取f1,2=0.5,通过计算灰置信水平来评估两者关联程度。若灰置信水平不小于90%,则认为轴承振动性能保持可靠性和振动性能退化概率关系密切;否则不密切。

3 案例分析

3.1 案例一

该案例为对轴承内沟道表面加入点蚀缺陷,从而引起振动加速度演变的仿真案例。数据来自美国Case Western Reserve University的轴承数据中心网站[22],该中心拥有一个专用的滚动轴承故障模拟实验台。该实验台包括1个2马力(约1.5kW)的电动机,1个转矩传感器/译码器和1个功率测试计等。待检测的轴承支撑着电动机的转轴,驱动端轴承型号为SKF6205,风扇端轴承型号为SKF6203。用加速度传感器测量轴承振动加速度信号。采用的驱动端转速为1 797 r/min、采样频率为12 kHz得到的轴承内圈有损伤的故障数据,损伤直径分别为0 mm,0.1 778 mm,0.533 4 mm和0.711 2 mm。所得轴承振动加速度的原始数据序列如图1所示。

图1 轴承在不同磨损直径下的振动信号Fig.1 Vibration signal of bearing under different wear diameters

由图1可知,随着磨损直径的增大,滚动轴承振动序列的幅值波动愈加剧烈,磨损直径大小直接影响滚动轴承的振动性能。而轴承磨损直径的尺寸表征着轴承损伤的严重程度:磨损直径越大,轴承损伤越严重。这也就意味着,随着滚动轴承损伤程度的加剧,滚动轴承振动序列的振动幅值波动愈加剧烈,滚动轴承的振动性能在逐步恶化。

以损伤直径为0 mm时获得的振动数据序列为本征序列,以磨损直径为0.177 8 mm,0.533 4 mm和0.711 2 mm时测得的轴承振动加速度数据序列分别看作是第2,3,4个振动序列,如图1所示。由式(4)～式(19)可得在置信水平P=95%条件下,本征序列的最大熵估计区间为[-0.111 4,0.123 5]。根据泊松计数原理,记录磨损直径分别为0 mm,0.177 8 mm,0.533 4 mm和0.711 2 mm时测得的各振动序列的1 600个性能数据落在本征序列最大熵估计区间[-0.111 4,0.123 5]之外的个数Nn,并求出变异频率θn和保持可靠度R(n),结果如表1和图2所示。

表1 保持可靠性参数和退化概率Tab.1 Parameters of continuity reliability and degradation probability

图2 轴承在不同磨损直径下的保持可靠度Fig.2 The continuity reliability of rolling bearing under different wear diameters

由图2可以看出,随着磨斑直径的增大,滚动轴承的振动性能保持可靠性在逐渐降低,说明轴承的运转性能在逐渐下降。磨损直径分别为 0 mm时,滚动轴承的保持可靠性较高,达到95.24%;当磨损直径分别为0.177 8 mm时,滚动轴承的保持可靠性下降到56.24%,下降幅度很大;而当磨损直径继续增大,也就是滚动轴承损伤程度进一步加重时,滚动轴承的保持可靠性也在继续下降,但是下降的幅度较第1次下降的幅度有所变缓。

由分析可以发现,基于最大熵法和泊松过程的滚动轴承振动性能保持可靠性模型可以准确地模拟出滚动轴承的可靠性演变历程。

由式(22)～式(27)分别求出振动序列X1、X2、X3、X4的自助最大熵概率密度函数(PDF),结果如图3所示。分别将X2、X3、X4的自助最大熵概率密度曲线与X1的概率密度曲线画在同一坐标系下,如图4所示,并求取重叠部分面积。

图3 振动序列的最大熵PDFFig.3 Maximum entropy probability density function (PDF) of the vibration series

图4 相似度法求退化概率Fig.4 Using the similarity method to find the degradation probability

由图4可以直观看出, 从X2到X4,它们与X1的重叠面积在逐渐减小。而PDF是在数据分布的层面上反映了序列的固有特征,所以这也可以认为,从X2到X4,它们与本征序列X1的相似度在下降。

为了进一步研究滚动轴承运转过程中的退化机理,由式(28)求出退化概率,结果如表1和图5所示。从图5可以看出随着滚动轴承的磨斑直径的增大,退化概率在逐渐升高。这也表明滚动轴承内圈表面的缺陷使其运转性能发生退化,并且缺陷越严重,轴承运转性能发生退化的概率越大。其中当磨斑直径由0 mm增大到0.177 8 mm时,滚动轴承的性能退化概率增长幅度很大;而当磨斑直径继续增大时,滚动轴承的性能退化概率虽也在增长,但是增长的幅度开始变缓。这一规律正好符合滚动轴承的性能保持可靠性的演变规律。

图5 轴承在不同磨损直径下的退化概率Fig.5 Degeneration probability of bearing under different wear diameters

为了定性分析滚动轴承振动性能保持可靠性与振动性能退化概率之间的关系,以退化概率Φ2为横坐标,保持可靠度Φ1为纵坐标,得到图6。由图6可以看出,随着滚动轴承的退化概率的增大,滚动轴承的振动性能保持可靠度在逐渐下降,两者在刻画滚动轴承振动性能演变历程上呈现反比关系。也就是说,滚动轴承性能的退化会导致保持可靠性的下降和退化概率升高。为了定量分析两者的一致程度,取退化概率序列的相反数作为Φ2=(0,-29.63,-52.85,-59.46),保持可靠度序列为Φ1=(95.24, 56.24, 49.44, 41.40),并由式(29)～式(40)对滚动轴承振动性能保持可靠性与振动性能退化概率进行灰关系分析,用灰色系统理论来评估它们关联程度。

图6 保持可靠性和与退化概率的定性关系Fig.6 The qualitative relationship between continuity reliability and degradation probability

在分析滚动轴承振动性能保持可靠性与振动性能退化概率之间的灰关系时,取参数f1,2=0.5,求出两者之间的灰置信水平为97.55%>90%,这表明Φ1和Φ2的关系非常紧密,说明滚动轴承振动性能保持可靠性与振动性能退化概率之间有明显的灰关系,可信水平达到97.55%。

3.2 案例二

该案例为在杭州轴承试验研究中心的ABLT-1 A型轴承寿命强化实验机上进行的滚动轴承疲劳寿命强化(快速)实验,实验设备如图7所示。该实验机主要由试验头、试验头座、传动系统、加载系统、润滑系统、计算机控制系统等部分组成。实验所用的轴承型号为7008AC/P2,数量为4套。轴向加载3.5 kN,径向加载2 kN,实验转速为4 000 r/min。每1 min记录1个振动数据,共记录8 400个振动数据,所得轴承振动加速度原始数据序列如图8所示。

图7 轴承寿命实验设备Fig.7 Bearing life test equipment

图8 轴承振动信号时间序列Fig.8 Bearing vibration signal time series

由图8可以看出,随着时间的推进,记录的滚动轴承振动加速度值在整体上呈波动上升趋势。当t≤2 800时,随着t的增加,振动加速度值略微下降后开始进入一个基本平稳阶段,这表示滚动轴承经过短暂的跑和期后进入正常运转期。当2 800

由式(4)～式(19)可得在置信水平P=95%条件下,本征序列的最大熵估计区间为[7.663 84,11.952 1]。根据泊松计数原理,记录振动序列X2和X3的各2 800个性能数据落在本征序列最大熵估计区间[7.663 84,11.952 1]之外的个数Nn,并求出变异频率θn和保持可靠度R(n),结果如表2和图9所示。

表2 保持可靠性参数和退化概率Tab.2 Parameters of continuity reliability and degradation probability

图9 不同振动序列的保持可靠度Fig.9 The continuity reliability of different vibration sequences

由图9可以看出,随着时间的推进,滚动轴承的振动性能保持可靠性在逐渐降低,说明轴承的运转性能在逐渐下降。在振动序列X1阶段,滚动轴承的保持可靠性非常高,达到97.14%,此时的滚动轴承处于最佳运转性能状态;在振动序列X2阶段,滚动轴承的保持可靠性下降到56.76%,下降幅度很大,说明滚动轴承发生了退化;在振动序列X3阶段,滚动轴承的保持可靠性继续下降,达到了38.25%,此时的轴承已经发生严重失效。但是下降的幅度,没有第1次下降的幅度大。上述分析表明,基于最大熵法和泊松过程的滚动轴承振动性能保持可靠性模型可以模拟出滚动轴承的可靠性演化历程。

由式(22)～式(27)分别求出振动序列X1、X2、X3的自助最大熵概率密度函数,结果如图10所示。分别将X2、X3的自助最大熵概率密度曲线与X1的概率密度曲线画在同一坐标系下,如图11所示,并求取重叠部分面积。由图11可以直接看出,从X2到X3,它们与X1的重叠面积在逐渐减小,这说明它们与本征序列X1的相似度在逐渐下降。

图10 振动序列的最大熵PDFFig.10 Maximum entropy PDF of the vibration series

图11 相似度法求退化概率Fig.11 Using the similarity method to find the degradation probability

由式(28)求出退化概率,结果如表2和图12所示。从图12可以看出随着时间的推进,滚动轴承的退化概率在逐渐升高。滚动轴承从振动序列X1变化到振动序列X2时,性能退化概率增长幅度较大;而当滚动轴承从振动序列X2变化到振动序列X3时,动轴承的性能退化概率虽也在增长,但是增长的幅度较小。这一规律和滚动轴承的性能保持可靠性的演变规律是一致的。

图12 不同振动序列的退化概率Fig.12 Degeneration probability of different vibration sequences

图13为保持可靠性和与退化概率的定性关系。由图13可以看出,随着滚动轴承的退化概率的增大,滚动轴承的振动性能保持可靠度在逐渐下降,两者在刻画滚动轴承振动性能演变历程上呈现反比关系。也就是说,滚动轴承性能的退化会导致保持可靠性的下降和退化概率升高。为了定量分析两者的一致程度,取退化概率序列的相反数作为Φ2=(0, -39.15, -75.21),保持可靠度序列为Φ1=(97.14, 50.76, 38.25),并由式(29)～式(40)对滚动轴承振动性能保持可靠性与振动性能退化概率进行灰关系分析,用灰色系统理论来评估它们关联程度。取参数f1,2=0.5,求出两者之间的灰置信水平为84.4%,这表明Φ1和Φ2两序列的关系比较紧密,说明滚动轴承振动性能保持可靠性与振动性能退化概率之间有明显的灰关系,可信水平达到84.4%。

图13 保持可靠性和与退化概率的定性关系Fig.13 The qualitative relationship between continuity reliability and degradation probability

5 结 论

本文提出一种基于最大熵法和相似度法的滚动轴承振动性能退化模型,并对滚动轴承的性能退化过程与其保持可靠性之间的关系进行研究。2个实验案例的结果表明,所提方法可以有效地对滚动轴承的退化特征进行提取和识别;滚动轴承振动性能保持可靠性序列曲线与性能退化序列曲线的变化趋势具有一致性,并且两者之间有明显的灰关系,可信水平均达到80%以上。

本文仅从对滚动轴承振动数据进行分析的角度,揭示了滚动轴承可靠性的演变历程与振动性能退化过程之间的内在关系,尚未涉及对滚动轴承进行动力学建模。下一步研究将从动力学角度分析二者之间的关系。