新型动态簇非平稳MIMO信道模型与信道特性分析
纪汪勇,张治中,邓炳光
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
移动-移动场景通信在多跳自组网、车辆通信系统、无人机通信系统中得到了广泛的应用[1-2]。当前第五代无线通信系统(5G) 移动-移动场景信道建模工作中引入了多输入多输出(Multiple-Input Multiple-Output,MIMO)技术,该技术能够显著提高通信系统的容量和效率[3],因此,采用MIMO技术的移动-移动场景通信系统逐渐成为研究热点[4]。同时,移动-移动场景通信系统中,移动发射机(Mobile Transmitter,MT)和移动接收机(Mobile Receiver,MR)都是运动的状态,因此,随着信道的环境不断变化,信道呈现非平稳特性[5]。为了有效地设计和优化移动-移动场景的通信系统,对通信系统的物理层建立准确可靠的信道模型至关重要。
早期的信道建模工作中通常假设信道满足广义平稳条件,当前,该类信道模型的研究比较成熟[6]。随着对新型移动-移动场景的信道测量研究发现,由于收发端的运动,散射体可能新生或消亡,多普勒频谱、路径时延、路径功率等呈现出非平稳时变特性[7-8]。文献[9]中提出了基于WINNER II单簇链路的时间演进信道模型,该模型将信道划分为几个独立的时间段,每个段采用WINNER II模型,但该模型建模较为复杂,且容易造成小尺度参数取值不连续。文献[10]中提出的非平稳通道模型应用了多天线,作者假设基于不同延迟的散射体簇和信道状态分布在多个圆柱上,通过追踪MT或MR的瞬时位置来更新,但该模型忽视了对簇的运动状态进行模拟。文献[11-12]中采用二维双簇链路,考虑了多反射散射体,但该模型忽视了单簇链路的影响。文献[13-15]中提出了基于无人机场景3D非平稳信道随机模型,但移动端速度都为固定的,不适用真实环境。文献[16]中将散射体的分布假设为两个规则的圆环并随收发端一起移动,同时用高斯-马尔科夫过程进行模拟,虽然较好地解决了收发端速度的任意性,但推导过程较为复杂。文献[17-18]中对3D非平稳移动信道进行建模,但该建模方法仅考虑信道时间域上的非平稳特性,忽视了阵列域非平稳特性影响。
本文在以往研究的基础上,提出了一种新型三维动态簇非平稳MIMO信道模型。该模型不仅结合了单簇-双簇-三簇链路,还模拟了收发端、散射体簇任意方向运动状态,将多种簇状态模型较好地融合;此外,采用马尔科夫生灭过程对阵列-时间域进行簇演进,提出了一种信道参数演进算法,并将该算法运用到动态簇信道建模中。
1 动态簇信道模型与信道特性分析
1.1 信道冲激响应
根据移动-移动场景的信道状态,在文献[9-15]基础上,提出了新型动态簇非平稳MIMO信道模型,这里采用双球几何模型来模拟该信道场景。如图1所示,MT和MR的天线阵列均为均匀线性阵列,MT第s根天线和MR第u根天线的三维位置坐标分别为dT,u和dR,u。图1中包括视距(Line-of-Sight,LOS)与非视距(Non-Line-of-Sight,NLOS)两部分,收发端间存在若干有效散射体;视距离开角的方位角为φT,LOS(t),离开角的俯仰角为θT,LOS(t),到达角的方位角为φR,LOS(t),到达角的俯仰角为θR,LOS(t)。同理,非视距动态簇链路的角度参数表示类似,在本图中未给出。在t时刻,MT、MR用vT(t)、vR(t)表示,各自的移动方向分别用俯仰角和同位角表示为θT(t)、φT(t)、θR(t)和φR(t)。

图1 M2M场景非平稳MIMO通信系统
移动发送端和移动接收端之间的小尺度衰落信道可以用一个复杂的矩阵hs,u(t)表示,其表示发送端第s根天线与接收端第u根天线之间的冲激响应,可由LOS分量与若干个NLOS分量之和表示:

(1)
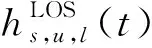
对于收发端的视距分量可以进一步表示为

fT,LOS(t)exp(jφLOS),

φLOS为视距随机初始相位。这里k=2πf/c,c为光速,f为载波频率。收发端天线坐标旋转矢量为
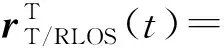
sinθT/R,LOS(t)sinφT/RLOS(t),
cosθT/R,LOS(t)],
速度矢量为
ST/R(t)=[sinθT/R,vt)cosφT/R,v(t),
sinθT/R,v(t)sinφT/R,v(t),cosθT/R,v(t)]T。
同理,收发端非视距分量可以进一步表示为

非视距时变相对偏移相位
非视距分量下单簇态多普勒相位偏移

同理,双簇态多普勒相位偏移
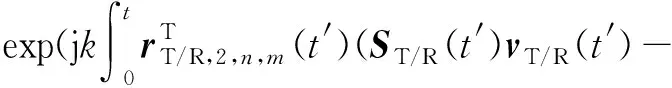
SC,T/R,2,n(t′))vC,T/R,2,n(t′)dt′),
三簇态多普勒相位偏移
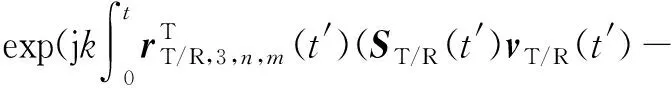
SC,T/R,3,n(t′)-SC,3,n(t))vC,T/R,3,n(t′)dt′),

1.2 信道参数演进流程
为了描述所提出的改进模型在移动-移动场景中的非平稳特性,本文在文献[16]的基础上提出了一种基于阵列-时间信道参数演进算法,算法描述如下:
/*总时间time,LT,LR分别为天线数量,NT,1(t0),NR,1(t0)分别为收发端第一根天线初始簇数量 */;
Input time,Δt,LT,LR,NT,s(t0),NR,u(t0)
根据阵列域马尔科夫生灭过程分别计算t时刻发送端天线s和接收端天线u的可视簇数目NT,s(t0),NR,u(t0);
使用洗牌随机配对算法[17],在收发端簇生成公共簇,配对簇作为双簇处理,未配对的簇作为单簇处理,对于近场的双簇做三簇处理,在双簇间随机生成生成第三簇,这里用Nl(t)(l=1,2,3)表示;
/*根据时间域马尔科夫生灭过程,对收发天线间的有效簇Nl(t)(l=1,2,3)进行时间域上的簇整体个数演进*/;
Whilet<=time do
forl=1:1:3
fori=1:1:Nl(t)
更新簇i的地理位置;
if 有新簇生成 then
if 新簇属于Nl(t) then
随机生成新簇位置、速度和速度方向;
计算小尺度参数;
将新簇添加到Nl(t)中;
end if;
end if;
end for;
end for;
t=t+Δt
end
1.2.1 生成簇时延
在生存间隔期间,时延参数与收发端位置以及簇位置有关,收发端的时变位置坐标表示为
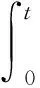
单簇链路位置为
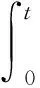
双簇链路
DC,T/R,2,n(t)=DC,T/R,2,n(0)+
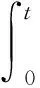
因此,视距时延
τLOS(t)=(‖DT(t)-DR(t)‖)/c,
非视距单簇和双簇链路时延分别为
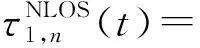
(2)

‖DT(t)-DC,T,2,n(t)‖+
(3)
同理,三簇链路的位置可以进一步表达为
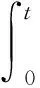
(4)
因此三簇链路时延为

‖DT(t)-DC,T,3,n(t)‖+
‖DR(t)-DC,R,3,n(t)‖+
‖DT(t)-DC,T,3,n(t)‖+
‖DC,T,3,n(t)-DC,3,n(t)‖+
(5)
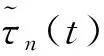
1.2.2 生成簇功率
l簇第n条NLOS路径的功率可以通过对应的路径延迟来计算,可得
(6)
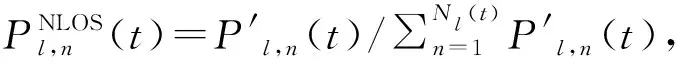
1.2.3 生成到达离开角
文献[18]已经证明,方位角和仰角在某些情况下是相互依赖的,并且测量数据表明Von Mise 分布能很好地模拟真实环境。为了使该模型更具有普遍性,本文模拟俯仰角θψ、方位角φZ服从Von Mise联合分布,可得
Ωψ,m(φψ,θψ)=
(7)
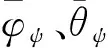
1.3 信道特性
1.3.1 空时相关性
在文献[11]的基础上,本文对新模型时空相关函数进行了推导,可得出hs,u,n(t)与hs′,u′,n(t)信道空时相关函数为
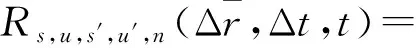
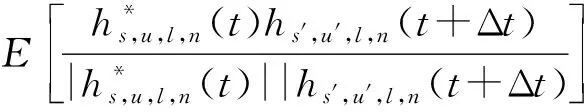
(8)


(ρT/R,s′/u′,LOS(t+Δt)-ρT/R,s/u,LOS(t))×
(fT/R,LOS(t+Δt)-fT/R,LOS(t)),
(9)

(10)
1.3.2 空间互相关函数
将Δt=0代入式(6)空时相关函数变成空间互相关函数(Cross-correlation Function,CCF):
(11)
同时由式(7)和式(8)可得视距和非视距条件下CCF分别为
(12)
(13)
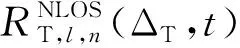
(ρT/R,s′/u′,l,n(t)-ρT/R,s/u,l,n(t))dφT/R,l,ndθT/R,l,n)。
(14)
1.3.3 时间相关性

(15)
同理,由式(7)和式(8)可得视距和非视距条件下的ACF分别为

(ρT/R,s/u,LOS(t+Δt)-ρT/R,s/u,LOS(t))×
(fT/R,LOS(t+Δt)-fT/R,LOS(t)),
(16)
(17)
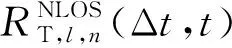
(ρT/R,s/u,l,n(t+Δt)-ρT/R,s/u,l,n(t))×
(fT/R,l,n(t+Δt)-fT/R,l,n(t)))dφT/R,l,ndθT/R,l,n。
(18)
2 仿真分析
为了进一步研究阵列域和时间域信道的非平稳特性,同时验证本文非平稳信道CCF和ACF理论表达式的正确性,本文仿真参数设置如表1所示。

表1 系统仿真参数
图2给出了Dc分别为10、30、100和500四个场景因子下的收发端多倍波长间距下簇生存率。从图中可以看出,场景因子越大簇生存概率越高,并且随着收发端阵列间隔增加簇生存概率下降。
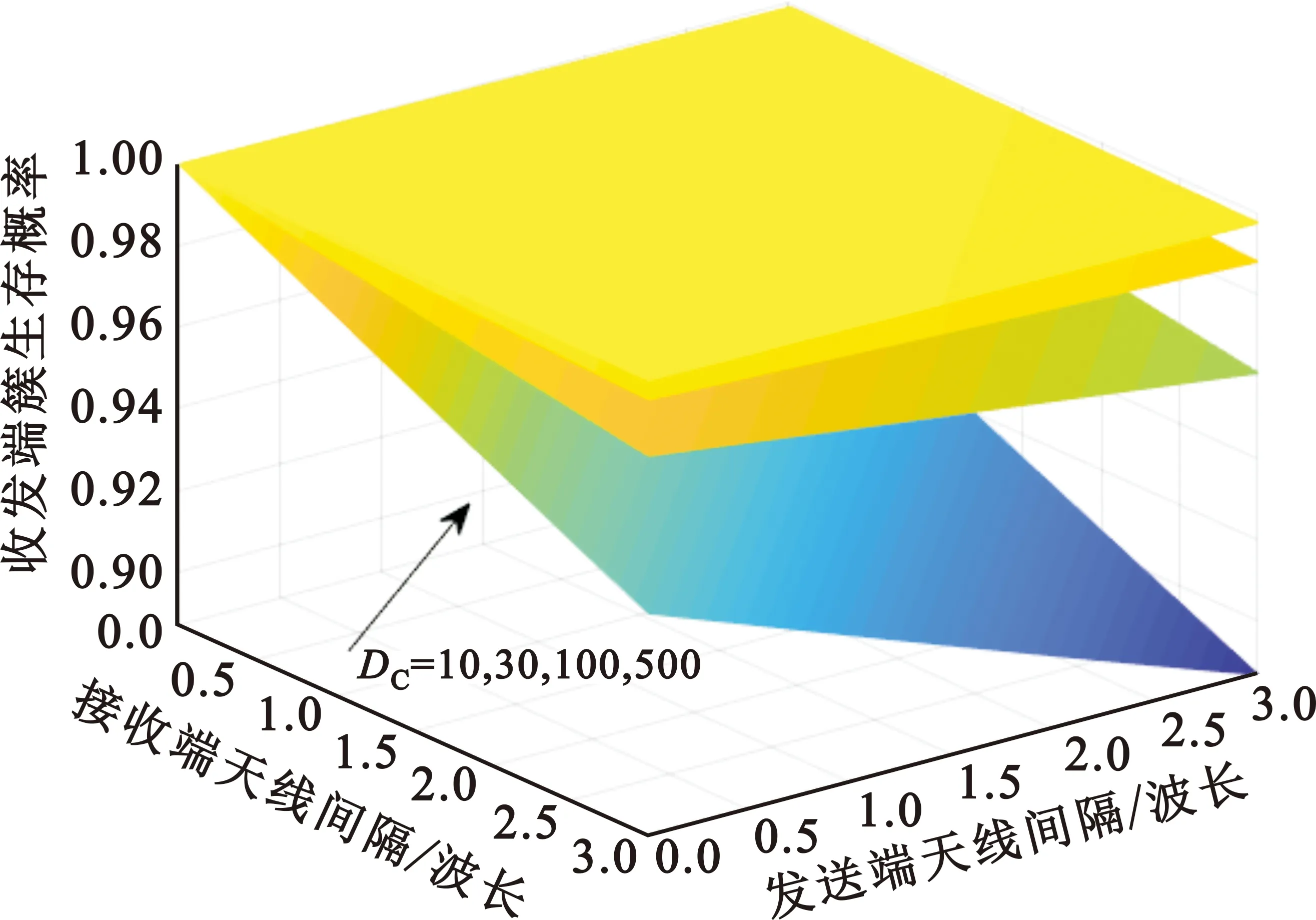
图2 阵列域收发端生存概率
图3和图4是经阵列域的簇演进后,对发送端第5根天线与接收端第2根天线可视的公共簇N5,2(t)={2,4,5,6,8,9,13,17,19,21,22,24}进行时间域演进,DC=10时,分别演进收发端和簇平均速度之和为3 m/s和6 m/s簇生灭情况,结果表明,当速度增加时,生存间隔越短,生存概率越小,导致生灭过程更加频繁。
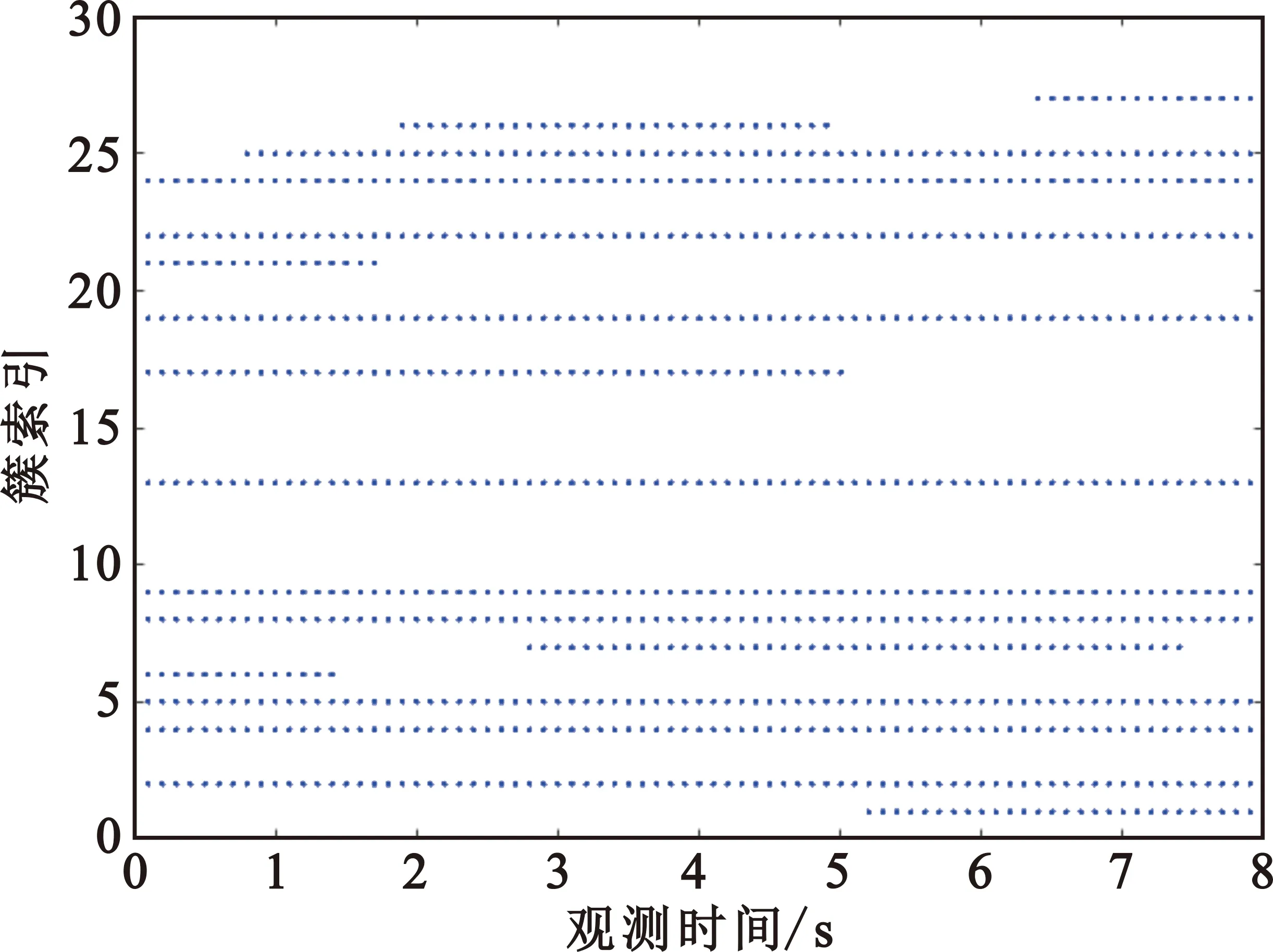
图3 速度3 m/s收发端簇变化

图4 速度6 m/s收发端簇变化
设置Δt=0,CCF的绝对值表示为|ρ1,1,2,2,n(ΔT,ΔR,t)|,如图5所示,当接收或发射侧天线间距增大时,CCF的绝对值平稳下降。同时,天线间距大于0.5倍波长时,CCF的绝对值将近为零,这一发现与以往结果较为吻合。
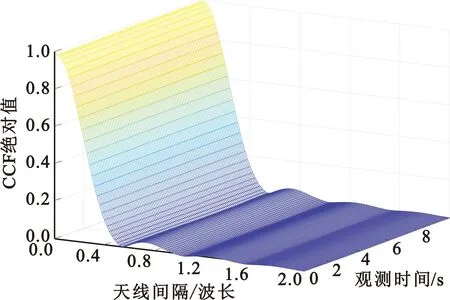
图5 Δt=0时非平稳信道模型CCF的绝对值
设置Δt=0和ΔR=0,CCF的绝对值|ρ1,1,2,2,n(ΔT,0,t)|如图6所示。从图中可以看出,在不同的时刻波形较为接近。图6还给出了t=0 s和t=5 s时,动态簇模型的理论值与仿真值,从图中可以看出理论值与仿真值拟合度较高,验证了推导CCF的正确性。同时,在未考虑阵列域天线切换情况下,相关函数波动几乎为零,这一情况说明了未考虑阵列间非平稳特性的CCF正确性。

图6 Δt=0、ΔR=0 CCF的绝对值
设置Δr=0,ACF的绝对值|ρ1,1,n(Δt,t)|如图7所示。当时间间隔增大时,ACF的绝对值平稳下降;当t增大时,ACF的绝对值变化加快。这一现象是由多普勒频移造成的,时间越大,在加速情况下速度越大,多普勒偏移越大,这一现象与真实场景较为接近。

图7 Δr=0时ACF的绝对值
在文献[9-15]单簇或者双簇模型的基础上,设置Δr=0,ACF的绝对值|ρ1,1,n(Δt,t)|,图8给出了t=3 s和t=7 s单簇、双簇和动态簇模型理论值与仿真值。动态簇模型的ACF曲线与单簇或双簇模型的ACF曲线非常接近,而且还弥补了只考虑单簇群或双簇链路的局限性。这表明动态簇模型可以替代单簇或双簇模型,而且理论值与仿真值拟合度较高,验证了推导的ACF的正确性。
3 结束语
本文基于移动-移动场景对载波为6 GHz的MIMO系统提出了一种新型三维动态簇非平稳MIMO信道模型。该模型不仅对阵列域和时间域上的非平稳特性运用马尔科夫生灭过程进行模拟,同时采用动态簇链路,在此基础上提出了一种信道参数演进算法。仿真结果表明,仿真模型的信道特性与理论模型一致,可以作为移动-移动场景的信道模型参考方案。由于移动-移动场景信道变化的复杂性,提出的信道模型的某些参数还需要通过相关的信道测量值进行进一步验证,这将是我们接下来的研究工作。

