模块化生产模式下的服装产品组合优化决策
韩曙光, 颜伟雄, 胡觉亮
(1. 浙江理工大学 理学院, 浙江 杭州 310018; 2. 浙江理工大学 服装学院, 浙江 杭州 310018)
服装产品组合决策是服装零售商的重要经营问题。零售商需要提供多款式的服装来满足消费者的个性化需求。在消费者需求越来越多元化的今天,对服装部件元素、款式和版型进行多样化的模块化组合生产,可以快速满足消费者的需求[1]。然而,如何选择由供应商提供的多款式服装是一个非常具有挑战性的问题,因为这需要权衡消费者的选择偏好和零售商可能的盈利情况等。零售商要获得利润最大化的服装产品组合,最简单的方法就是穷举所有可能的服装组合,然后选择利润最大的组合;然而同一款风格的服装,往往具有多种垂直差异化产品[2],不可能对其一一罗列,这样很难通过穷举确定最优的产品组合。
近年来,模块化的思维设计方法开始运用到服装上,将服装部位进行模块划分,在部位模块上增添或删减元素,设计出具有多样性和新颖性的服装产品族[1,3];此外,在服装工艺生产中,有学者提出将服装工序进行模块划分,并运用于服装智能传输系统,可有效改善现有服装流水生产[4-5]。现已有企业在服装个性化定制方面应用模块化生产:辛巴达作为一家专注于服装生产的柔性供应链平台,划分有打板、裁剪、缝纫、面料多个模块工厂,运用互联网技术对传统工厂进行模块化改造,取得了一些进展[6];国外李维斯推出Future Finish线上服务,采用模块化设计技术理念,对牛仔裤进行自主模块设计,实现牛仔裤数字化开发与生产[7]。因此,市场上产生了越来越多垂直差异化的多款式服装产品,单一产品的经营策略是不可取的,提供多属性且不同质量水平的产品策略才是最优的[8-9]。零售商需要根据消费者类型、产品价格、产品质量、产品的搜索成本以及产品规格大小等因素[10-12]对产品进行正确的组合决策。
本文主要讨论模块化服装的产品组合优化问题。在模块化生产模式下,生产垂直差异化服装,分析模块化服装时尚度对消费者在服装选择性上的影响,讨论为获得利润最大化,零售商对多款服装进行产品组合决策;本文还研究了在多款式的服装市场环境下,寡头供应商与多个不同产品组合决策的零售商进行最优的利润分配等。
1 问题描述与符号说明
传统服装生产是以服装成衣为单位,按直线型流水作业,依次传递生产;而模块化生产,则是结合服装工艺和服装结构划分进行作业调整,摆脱传统的设计生产模式束缚,将服装部件模块化分割,组合出造型元素时尚度不同和款式多样化的服装。
对于多款由模块化组成不同时尚度的垂直差异化服装,零售商需要根据市场消费者偏好对服装产品进行组合决策。本文考虑在需求确定下,构建基于效用最大化的消费者选择模型,设计关于垂直差异化服装产品之间的有向图,以最短路径求得零售商最大利润的产品组合。此外,进一步考虑,多零售商在不同货架空间产生不同产品组合决策的情况下,供应商根据市场情况,通过最大流问题对多零售商进行合理的利润分配。
符号说明如表1所示,对服装产品组合有以下假设:1)不考虑销售周期末产品残值;2)不考虑补货情况;3)每位消费者最多只购买单件产品;4)消费者心理估值服从均匀分布。

表1 参数定义Tab.1 Parameter definition
2 数学模型
本文将针对具有垂直差异的模块化服装产品构建服装时尚度模型、消费者选择模型和需求确定时零售商以及供应商决策模型。
2.1 模块化服装时尚度模型
服装具有典型的季节性,其时尚度很大部分取决于服装产品内包含的时尚元素:款式、花色图案以及装饰配件等[13-14]。假定服装是由部件模块和部件造型模块组成[15],由于是垂直差异产品,其服装风格固定,故服装时尚度是在部件模块的基础时尚度上,对其他部位进行造型模块的选择,可以组成多款时尚度不同的服装。
部件模块可分为衣领、衣身、袖子、门襟、廓形等,而造型模块是在部件模块的基础上进行多个属性细分。由于服装各部件的模块都有其相应的服装时尚元素,各属性数值按该周期流行趋势的时尚指数表示[13],由多个包含属性的模块向量组成矩阵[16],用0~1规划整合求得时尚度。某部件i的属性向量为Xi=(xi1,xi2,…,xij,…,xim)。yij=1表示选择了时尚度为xij的部件造型;yij=0表示未选择时尚度为xij的部件造型,则部件造型选择向量为Yi=(yi1,yi2,…,yij,…,yim)。
服装时尚度wj是由基础款式的时尚度w0和各部件造型模块的时尚度累加求和得到,其表达式为
(1)
故多款不同组合时尚度不同的服装,其各款服装的时尚度关系为:0≤w1≤w2≤…≤wj≤…≤wn。
2.2 消费者选择模型
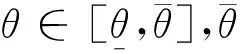
(2)
依据文献[17],假设消费者估值分布函数为F(θ)=1-(1-θ)b,b>0,消费者根据效用最大来购买产品,由此得到的购买概率为
(3)
为保证αj≥0,即购买概率不小于零,需满足式(2)。
2.3 单一零售商决策模型
假设产品需求确定,存在一个零售商,不考虑商品库存、货架空间且不存在竞争关系,根据到店消费者人数μ和购买概率αj,可确定产品j的需求量为Dj=μαj,则零售商利润函数表示为
(4)
寻找垂直差异化产品的最优组合,即极大化利润函数:
(5)
2.4 市场利润分配模型
从市场利润最大化的角度看,假设单寡头的服装供应商为零售商供货,而服装零售商在进货中,由于服装款式的多样性,每个零售商固定的货架空间η(η代表单位空间最大毛利润)是不同的。零售商为获得最大利润,需要根据自身的固定空间,有选择性地对服装款式进行组合入货,因此多零售商市场为获得更多利润,需要根据不同生产情况下的供应商为多个零售商进行合理供货。
将构造以寡头供应商为源点s,多个款式服装作为节点和市场消费群t为终点的有向无环图,通过最大流对市场t求最大利润分配。如图1所示,s为供应商,t为市场消费群,供应商s向市场消费群t输出款式为A和B的服装,其中s到t的1条路径代表一零售商。图中供应商到市场消费群有3条路径,每一路径表示为1种产品组合决策的零售商,故图中表示有3种不同产品组合的零售商(s→A→t,s→A→B→t,s→B→t),对3个零售商进行利润分配。该网络中的最大利润分配模型为
maxval(f)
(6)
f(vi,V)-f(V,vi)=0,vi∈M
(7)
f(s,V)-f(V,s)=val(f)
(8)
f(t,V)-f(V,t)=-val(f)
(9)
0≤fij≤ηij
(10)
式中:val(f)为服装款式网络流f的利润,最大利润分配为利润值最大的网络流;V={M,s,t},为网络顶点的集合;s为源点;t为终点;M={v1,v2,…,vm},为网络中除源点s和终点t之外的服装款式集合;fij为款式{i}与款式集合{i,j}的实际利润差;ηij为款式{i}与款式集合{i,j}的固定利润差。

图1 零售商选择决策Fig.1 Retailer selection decision
式(7)~(9)为利润流量的平衡约束。其中:式(7)表示中间节点的输入利润等于输出利润;式(8)、(9)分别表示源点和终点的输入利润流量等于其输出利润流量。式(10)为容量约束,即实际利润不能超过固定利润。
3 模型求解
3.1 最佳产品集合
通过满足式(11)~(13)的条件优化多产品集合,并构建产品间的一个有向图,通过最短路径对式(5)进行零售商最大利润求解并获得最佳产品组合S*。
定理: 最佳组合S*产品集合满足以下3个条件[18]:
(11)
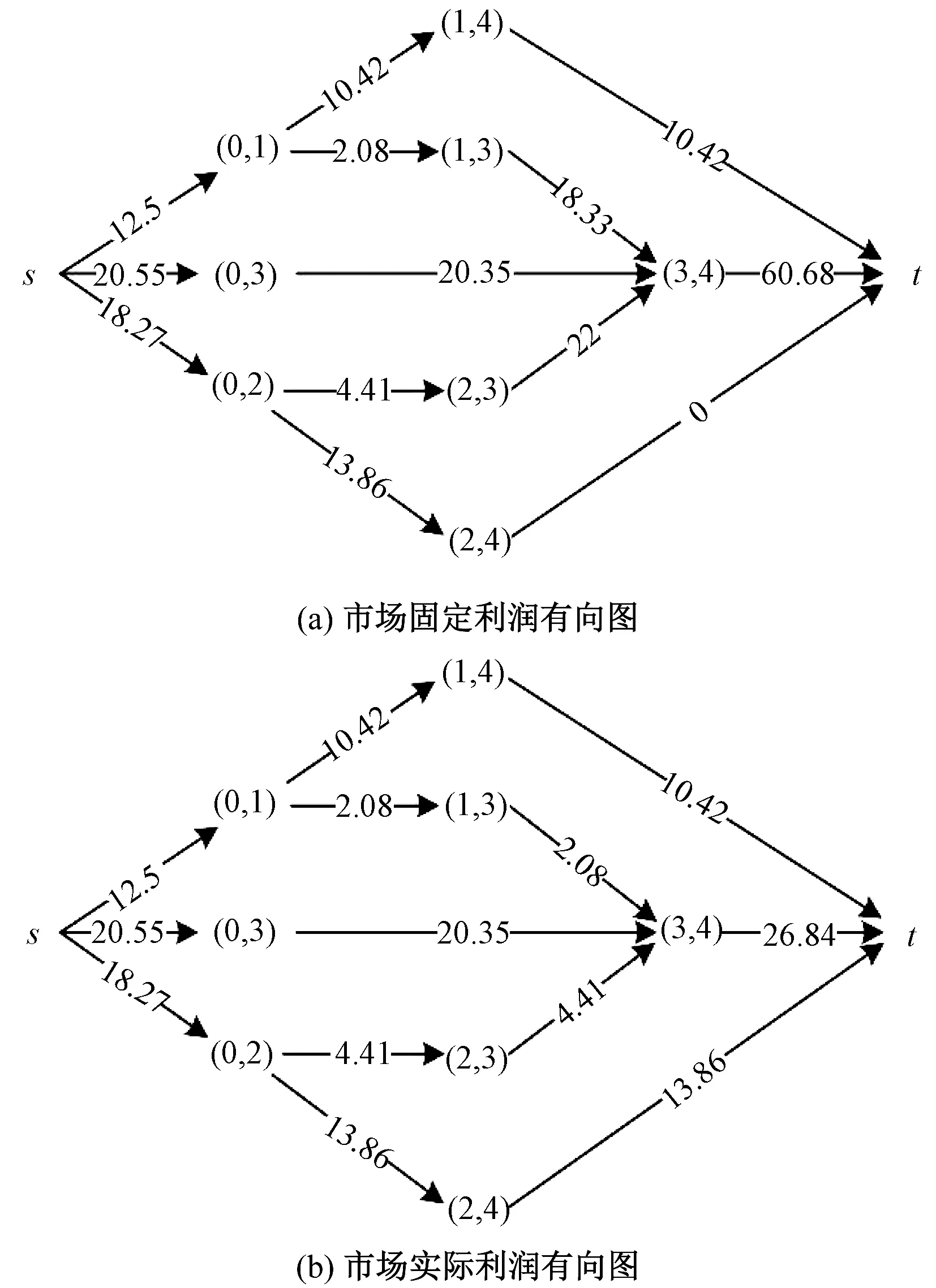
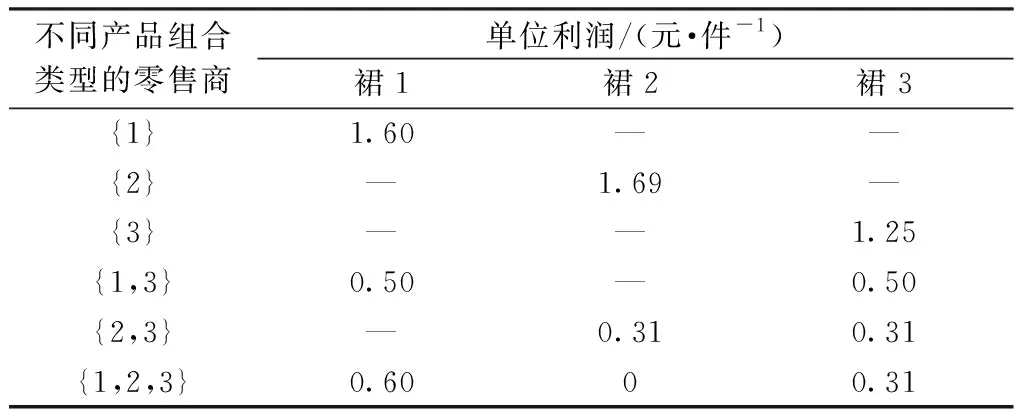
p1 (12) p1-c1≤p2-c2≤…≤pn-cn (13) 以上定理表明:在产品组合中,价格在时尚度水平上是严格递增的,式(11)、(12)是最佳产品组合的必要条件;利润在时尚度水平上是递增的,说明在服装周期内,根据服装部件模块的时尚元素选择,时尚度越高,价格也将随之递增;式(13)说明时尚度越高的服装,可获得更高的收益。 步骤1:构造节点集,引入源节点(0,0)和目标节点(n+1,n+1)。 V4={(0,0),(n+1,n+1)} V=V1∪V2∪V3∪V4 步骤2:节点之间弧的距离为 (14) 在有向图构造步骤中,n表示有向图中共有n款服装,引入0和n+1,分别表示产品集合的初始点和结束点,并不代表某一款式服装。式(14)是节点(i,j)与(j,k)之间的距离,表示产品j利润值的相反数。由于产品间的利润大小为负,即从(0,0)到(n+1,n+1)的路径值均为负,则得到的路径值越小,产品组合利润值越大,因此,可通过最短路径求得利润最大的服装产品组合。 步骤1:构造节点集,引入源节点s和目标节点t: V4={s,t} V=V1∪V2∪V3∪V4 步骤2:节点之间弧的距离为 (15) 由于将有向图的每个路径看作一种产品组合类型的零售商,式(15)为零售商在自身的货架空间下获得的最大固定利润。单一寡头供应商根据服装市场变化,从源点s为不同类型的零售商输出服装。供应商需要满足自身的最大输出,同时也要合理分配零售商的实际利润。因此,根据供应商与各类型零售商之间构建的有向图,将本问题转化为供应商对各零售商的最大流利润分配问题。 本文基于上文的求解方法,对模型进行求解分析,并讨论服装成本和其时尚度对零售商、供应商和整个供应链利润的影响。 如果使用穷举方法对3款裙子进行产品组合决策,则需要考虑7个分类:{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}。通过产品组合的优化设计,构造产品集,通过产品之间的利润弧线连接起来,以有向无环图(见图2)表示各产品之间有效路径的对应关系,图中坐标(i,j)表示由一对产品(i,j)∈V组成,(0,0)和(4,4)为源点和终点,节点之间权重表示产品间带负权值的单位利润。通过带负权值的最小路径计算服装零售商产品组合的最大利润。 图2 服装产品集合有向图Fig.2 Directed graph of apparel product set 图2所示网络包含5个有效路径,路径分类如表2所示。相比穷举7种产品组合路径,该组合优化的效果明显,可排除2个无效组合。 表2 有效路径与利润Tab.2 Effective path and profit 由上述分析可知,将多款服装进行有效组合,形成有效路径,由于每个零售商的货架空间产生单位利润不同,因此不同的零售商根据其货架空间进行最优产品组合决策,即每个零售商的最优产品决策各不相同。在时尚服装市场中,往往会存在供不应求和供过于求的情况,为了尽可能满足市场需求,在只有单一供应商下,供应商对多个不同产品组合类型的零售商进行合理的利润分配,使市场的利润最大化。 4.2.1 供不应求情形 图3 供不应求情形下市场的利润分配Fig.3 Profit distribution in market with short supply. (a)Directed graph of market fixed profit;(b)Directed graph of market actual profit 图3(a)中弧的容量大小表示产品的单位固定利润,即源点s向市场分配利润为:裙1的单位固定利润12.5元/件,裙2为18.27元/件,裙3为20.35元/件。源点s的单位固定利润小于终点t,说明市场对该季度系列服装需求过大,造成供不应求的状态。图3(b)中的弧表示产品实际的单位货架利润,供应商根据各货架空间不同的零售商,按照市场需求利润最大化,对零售商进行分配。求解得到市场最大单位利润为51.12元/件,各类型零售商服装组合中的单位利润如表3所示。 表3 供不应求情形下实际利润分配Tab.3 Distribution of actual profits with short supply 由表3可知,产品组合为{1},{2},{3}的零售商在供应商分配所获得的实际利润均比零售商{1,3},{2,3}高,因为供应商受到订货成本、运输装载成本和布料成本因素的影响,单个产品生产会大量减少供应商的其他开支成本,所以供应商更愿意为单个规格数量较多的零售商供货。 4.2.2 供大于求情形 图4 供大于求情形下市场的利润分配Fig.4 Profit distribution in market with oversupply.(a)Directed graph of market fixed profit;(b)Directed graph of market actual profit 通过计算,在供应商对多个零售商最大化利润分配下,市场得到的最大单位利润为5.95元/件。在供大于求的环境下,市场环境变为买方市场,零售商成为主导,供应商愿意把货尽可能销给零售商,但零售商需要根据自身需求情况进行订货。表4示出供大于求情形下实际利润分配。 表4 供大于求情形下实际利润分配Tab.4 Distribution of actual profits with oversupply 由表4可看出,产品组合为{1,2,3}的零售商,固定最佳组合是进货3件服装,由于市场情况,零售商对裙2所得到的利润为0,原因是为了保证零售店的产品多样性,得到最大利润;从表中同时可看出,零售商{2}获得的利润最大,其余是{1},{3},都是单款产品销售,很大原因是由于存在不同地区消费者的偏爱程度有所差异和市场供大于求,消费者不愿消费导致的。 本文基于服装的模块化生产,由供应商提供多款垂直差异化的服装产品,在消费者效用最大化和零售商利润最大化情况下,零售商对多款服装产品进行最优产品组合决策。 通过设计不同的模块化时尚度,寻找产品组合集合,构建一个有向无环图,将问题设计为一个最短路径问题,寻求利润最大的服装产品组合,相比于对所有服装进行穷举组合决策更加快速有效。本文进一步考虑零售商不同货架单位固定利润产生不同的产品组合,分析寡头供应商对市场最大利润分配的情况。当供不应求时,供应商为了节省资源,给愿意为产品款式需求较少的零售商配送,市场获得更大的利润;当市场供大于求时,服装零售商根据市场产品时尚度需求对产品进行合理组合。 本文对垂直差异化服装进行组合优化,为供应商分配和零售商订货提供一定的参考,但在本文研究中,只是定义服装零售商存在货架空间的单位固定利润所产生不同的产品组合情况,并没有对货架空间进行具体描述,也没有考虑缺货影响消费者产生替代的行为,这些都值得进一步探究。 FZXB3.2 服装产品组合优化决策
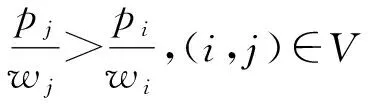
3.3 供应商与零售商之间的最大利润分配
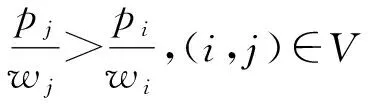
4 算例分析
4.1 服装垂直差异化最佳产品组合
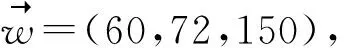



4.2 市场利润最大化


5 结 论

