智能算法在电网负荷预测中的应用研究

王世芳，鲍程程

(1.安徽工程大学 电气工程学院，安徽 芜湖 241000;2.西南大学 电子信息工程学院，重庆 400715)

电力系统在全国经济发展中的作用至关重要，对电力负荷预测的精准程度与国家的发展以及经济效益息息相关，因此电力负荷预测在当代已成为众多学者的研究课题。对于受到越来越多因素影响的电力负荷预测，传统的凭借经验的预测方法已不适用于当下。在前人研究的基础上，挑选了两种较为精确的方法对电力负荷进行预测，分别是灰色系统理论与多元线性回归模型。灰色预测理论是针对包含已知与未知信息的系统进行预测，即通过已知的用电量数据来预测未来的电力负荷，而多元线性回归模型是以电力负荷为因变量，多个影响电力负荷的因素为自变量进行预测，最后分析两种方法的预测精度，对比哪种方法更适合对未来电力负荷进行预测。理论上这两种方法都适用于当下受多重因素影响的电力负荷预测，预测结果表明两种精度都适合电力负荷预测。

1 灰色预测理论模型

1.1 灰色预测模型的建立

电力负荷预测是通过利用已有的原始数据以及相关信息，找出电力负荷变化的规律，从而预测其未来的变化情况。随着经济的发展，传统的负荷预测方法已不适应长期电力负荷预测理论的要求。灰色理论把随机量当作是在一定范围内变化的灰色量，将无规律的历史数据累加生成特定序列来构建微分方程模型。研究在对芜湖市市辖区电力中长期负荷预测的研究中引入了灰色预测理论的建模方法以及残差分析，简化了问题，保证了预测精度的要求。

取安徽省芜湖市市辖区的长期电力负荷情况的原始数据

x

(

j

)为

GM

(1,1)建模序列：

x

(

j

)={

x

(1),

x

(2),

x

(3),…,

x

(

m

-1),

x

(

m

)},

(1)

在求取

GM

(1,1)模型时,首先要对芜湖市市辖区近几年电力负荷情况进行一阶累加生成新的序列，即AGO序列令为

x

(

j

)={

x

(1),

x

(2),

x

(3),…,

x

(

m

-1),

x

(

m

)},

(2)

其中，

x

(1)=

x

(1),

(3)

x

(2)=

x

(1)+

x

(2),

(4)

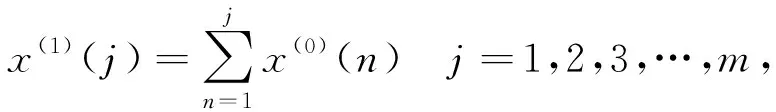
(5)

取

x

(

j

)的均值序列令为

y

(

j

)，取

y

(

j

)为白化背景序列值：

y

(

j

)=0

.

5

x

(

j

)+0

.

5

x

(

j

-1),

(6)

y

(

j

)={

y

(2),

y

(3),

y

(4),…,

y

(

m

-1),

y

(

m

)},

(7)

对新生成的序列建立

GM

(1,1)灰的微分方程：

x

(

j

)+

cx

(

j

)=

d

,

(8)

式中，

c

，

d

为特定的参数。

c

为发展系数，它的选取可以适当提高背景值的精确度；

d

为灰作用量，由于

d

是我们计算得来的，相当于作用量，是具有灰的信息覆盖的作用量。对新生成的序列建立

GM

(1,1)白化形式的微分方程：

(9)

I

=(

A

A

)

A

z

，

I

可通过最小二乘法求出，

z

=

AI

。式中,

A

为数据矩阵，而(

A

A

)

A

是数据矩阵

A

的广义逆矩阵；

I

是参数向量；

z

是数据向量。

(10)

z

=[

x

(2),

x

(3),

x

(4),…,

x

(

m

-1),

x

(

m

)]。

(11)

通过式(9)可求得微分方程的解，然后就得到

GM

(1,1)预测模型如下：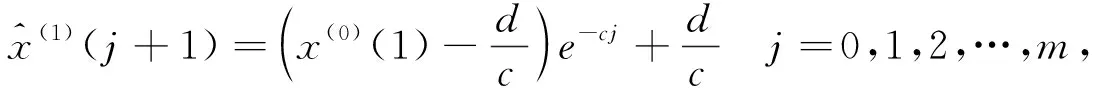

(12)

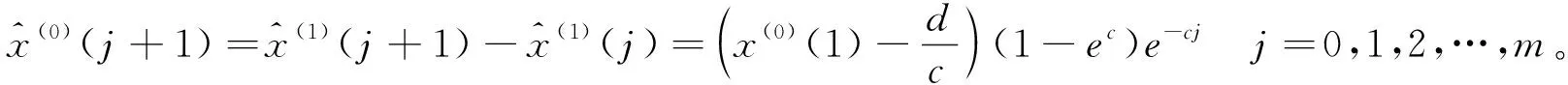
(13)

1.2 灰色预测模型的精度检验

在建立

GM

(1,1)预测模型后，要对其进行精度检验，判定所建模型是否合理，只有通过检验的模型才能用来作预测，灰色预测模型的精度检验一般有三种方法：相对误差大小检验法，关联度检验法以及后验差检验法，如表1所示。研究主要介绍后验差检验法。计算残差得

(14)

(15)

(16)

(17)

后验差比值为

(18)

式中，

P

与

C

是后验差检验法的两个重要指标。其中，

C

越小越好，

C

越小则

S

越大，而

S

越小。

S

大则样本数据方差大，即样本数据离散程度大；

S

小则残方差小，即残差数据离散程度小。

C

小则尽管样本数据离散，而

GM

(1,1)模型计算的预测值与实际值相差不是很离散。

1.3 实例分析

2002～2012年安徽省芜湖市市辖区每年用电量如表2所示，预测的用电量如表3所示。由表3可知，2002～2012年芜湖市市辖区用电量的平均误差为5

.

37%，最大误差为13.76%，而2011年预测的相对误差只有0.37%，均方差比值

C

=0

.

1，后验差比值

P

=1，则说明系统预测精度好，对本组选取的数据而言，该预测精度足够对未来用电量进行预测。

表1 精度检验表

表2 2006～2012年芜湖市市辖区用电量(×108 kW·h)

表3 芜湖市市辖区用电量预测(×108 kW·h)

1.4 仿真图与流程图

灰色预测理论仿真图如图1所示。灰色预测理论模型程序流程图如图2所示。

图1 灰色预测理论仿真图图2 灰色预测理论模型程序流程图

2 多元线性回归模型

2.1 多元线性回归模型的建立

多元线性回归模型与一元线性回归有些相似，多元线性回归是分析两个或以上的自变量与一个因变量，其中，自变量与因变量呈现线性关系。我们通过多个自变量对因变量进行估计，能够达到预想的效果，同时更加符合实际情况。一般设有

r

个影响因素，即自变量分别为

A

,

A

,…，

A

,因变量为

B

，(

a

1,

a

2,…,

a

,

b

)(

i

=0,1,…,

m

)为(

A

,

A

,…,

A

,

B

)的实验数据，即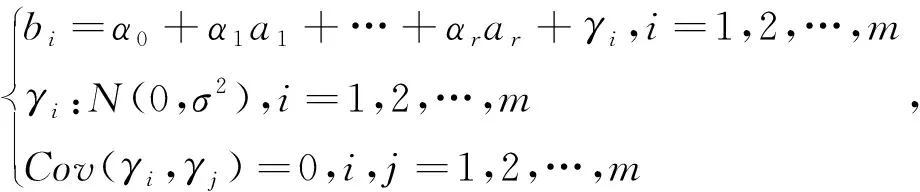

(19)

式中，回归系数

α

(

i

=0，1,…,

r

)与

σ

都是未知的，

γ

是随机误差。取

α

=(

α

,

α

,…,

α

)，

B

=(

b

,

b

,…,

b

)，

γ

=(

γ

,

γ

,…,

γ

)，其中，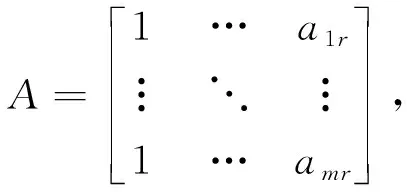

(20)

则多元线性回归模型为

(21)

(22)

(23)

残差平方和为

(24)

对给定观测数据(

a

1,

a

2,…,

a

,

b

)(

i

=0,1,…,

m

)而言，

α

选择式(25)的最优解。

(25)

(26)

2.2 实例分析

研究以芜湖市市辖区的用电量为因变量，以2002～2012年芜湖市市辖区的GDP以及人口为自变量进行电力负荷预测。该多元线性回归模型将采用Excel软件进行相关问题的分析处理，通过选中Excel菜单栏中“工具”的“加载宏”命令，选择“分析工具库”中的“数据分析”里的“回归”，即可进行分析预测。

(1)线性回归分析。以芜湖市市辖区用电量为因变量

Y

，GDP和人口为自变量

X

、

X

，用Excel进行线性回归分析，2002～2012年芜湖市市辖区用电量与GDP、人口数据如表4所示。

表4 2002～2012年芜湖市市辖区用电量、GDP与人口数据表

(2)线性回归结果检验。

①回归统计表如表5所示。由表5可知，复相关系数

Multiple

R

是0

.

993 58，则GDP与芜湖市市辖区用电量的关系呈高度正相关；而多重判定相关系数

R

Square

即复相关系数的平方，表现的是自变量解释因变量变差的程度，

R

Squsre

为0

.

987 20；修正多重判定系数

Adjusted

R

用于多元回归，

Adjusted

R

为0

.

983 99，其拟合优度较高，表明芜湖市市辖区用电量有98

.

399%由人口与GDP决定，标准误差表明观测值与趋势值平均离差。

表5 回归统计表

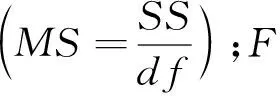
表6 方差分析表

该计算中用每个平方和分别除以总平方和，4 111

.

415(

SS

列的回归分析)÷4 164

.

746(

SS

列的总计)=0

.

987 20(多重判定相关系数)，即GDP及人口对芜湖市市辖区用电量影响为98

.

72%，残差变量影响了剩余的1

.

28%(52

.

330(

SS

列残差)÷4 164

.

746(

SS

列总计))；由

F

值计算得到的

P

值为2

.

69

E

-08(实际值为0

.

000 000 026 9)，小于置信水平0

.

05，表明回归方程的回归效果显著，因此可以用自变量的变化解释因变量的变化。③回归系数的显著性检验表如表7所示。由表7可知，数据都是截距与斜率的各项指标，依次为非标准化的偏回归系数，偏回归系数的标准误差，原假设为0的样本统计量，各系数

P

值及置信区间上下限。GDP回归系数为0

.

055 52，

P

值为0

.

000 01，表明该回归方程中变量GDP有统计学意义。由表7第二列的值可知，芜湖市市辖区电力负荷预测回归方程式为：用电量=-0

.

553 82+0

.

055 52×GDP+0

.

095 23×人口，通过GDP数据可对芜湖市市辖区用电量的电力负荷进行定量预测。

表7 回归系数的显著性检验表

如2013年芜湖市市辖区人口为136

.

10万，GDP为1 269

.

08亿元，用电量为83

.

16亿千瓦时，则由上述回归方程式可求得：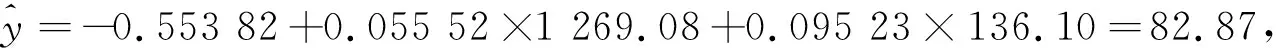

(27)

由回归方程得到的用电量与实际值有一定误差，但是并不影响多元线性回归模型的有效性。

④观测值与预测值对比如表8所示。由表8与表4对比可知，Excel拟合结果与算法预测结果基本一致，各年用电量预测的平均相对误差为5.62%，2004年电力负荷预测的相对误差低至0.52%，最大的相对误差是15.76%。综上，准确的用电量的预测必须建立在准确的GDP及人口数据基础上，复杂以及经常变动的经济环境可能会影响GDP及人口预测的准确性，带来一些误差，但这对线性回归模型有效性影响不大，本回归模型及结果可以作为负荷预测的科学依据。

表8 Excel拟合所得观测值与预测值对比表(×108 kW·h)

(3)拟合结果。GDP与芜湖市市辖区用电量拟合情况如图3所示。人口与芜湖市市辖区用电量拟合情况如图4所示。利用Excel中显示趋势线的公式与

R

的平方值生成趋势线，得出回归线性方程。由图3可知，用电量与GDP的回归方程为

y

=0

.

061 2

x

+5

.

662 7，其中，

R

=0

.

997 9，

R

是

Y

的预估值与实际值之比，其越接近1，说明线性拟合效果越好，相关性越强。由图4可知，人口与用电量的回归方程为

y

=0

.

844 2

x

-43

.

794，其中，

R

=0

.

839 1，表明该回归模型所预测的负荷有较高的预测精度，可用来对芜湖市市辖区未来几年负荷进行预测。

图3 GDP与芜湖市市辖区用电量拟合情况图4 人口与芜湖市市辖区用电量拟合情况

3 结论

对芜湖市市辖区2002～2012年用电量分别采用灰色预测理论模型以及多元线性回归模型的方法进行预测，预测值如表9所示。表9对应的拟合图如图5所示。对两种方法所得预测值分别进行了相对误差计算，计算结果如表10所示。

表9 芜湖市市辖区用电量观测值与两种方法所得预测值对比表(×108 kW·h)

图5 观测值与两种方法所得预测值对比图

表10 两种方法误差对比表

通过上述计算以及Matlab仿真与Excel拟合结果可知，当分别采用灰色预测理论即多元线性回归模型对2002～2012年芜湖市市辖区用电量进行预测时，两种方法预测结果的精度都符合要求，但二者是有差异的。由灰色预测理论预测得到的平均相对误差不到5.37%，最大相对误差是13.76%，而由多元线性回归模型预测得到的平均相对误差为5.62%，比灰色预测理论模型平均相对误差高，多元线性回归模型的最大相对误差是15.76%。由此可见，灰色预测理论模型更适合对未来中期电力负荷进行预测。

对于其他案例应用灰色预测理论，如果精度不够，还可以对其进行改进。通过建立残差序列进行修正，或者对原始数据加以处理，都可以提高

GM

(1,1)模型的精度。灰色预测理论相对于多元线性回归模型而言，不用考虑多个自变量的影响，只需要一组原始数据就可以对用电量进行预测，需要的数据少，方法简单。研究分别利用灰色预测理论与多元线性回归模型两种算法对芜湖市市辖区的用电量进行负荷预测，有一定的实用价值，而同类成果只采取了其中某一种方法进行负荷预测，没有进行算法的对比，实用性一般。