基于支持向量机的复杂曲面磨削去除量预测*
赵敬川,赵吉宾,李 论,张洪瑶
(1.中国科学院沈阳自动化研究所机器人国家重点实验室,沈阳 110016;2. 中国科学院机器人与智能制造研究所,沈阳 110169;3.中国科学院大学,北京 100049)
0 引言
在传统的高精度复杂曲面磨削加工中,采用的是以下几种磨削方式:专用机床磨削加工、人工磨削加工以及数控机床磨削加工。这些磨削加工方法都具有一些的不足,例如专用机床磨削加工的通用性较差,成本高,无法满足个性化、小批量生产;人工磨削加工则磨削速度慢,工人工作环境差,而且加工精度难以保证;数控机床磨削加工柔性较差,可拓展范围不大,同时数控机床的加工成本高。最近几年随着机器人的快速发展,机器人在磨削加工领域的应用得到人们的高度重视。
尽管工业需求较大,可是当前对于复杂曲面的大多数机器人高精度磨削系统仍然处在研究阶段。近几年,学者们提出了工业机器人修型磨削问题。工业机器人修型磨削指的是利用工业机器人系统以及砂带磨削系统对航空发动机叶片等复杂曲面工件外表面开展磨削加工,从而使产品满足设计生产要求的一种高精度磨削加工过程[1]。
由于机器人修型磨削十分复杂,磨削去除量的外部影响因素较多,众多科研人员针对这一问题开展了多种磨削去除量预测理论的相关研究。文献[2]通过分析实验结果得出对于磨削去除量而言,磨削力大小的影响系数最大;文献[3]通过人工神经网络预测算法对电火花加工的工件表面质量开展了预测实验,收到了很好的预测结果; 文献[4]通过建立人工神经网络预测模型,开展了针对仿形加工中工件去除率的预测实验研究。尽管文献[3-4]建立了基于神经网络预测算法的磨削去除量预测模型,而且收到了不错的理论预测结果,但是基于神经网络算法进行预测仍然存在很多缺陷,例如容易出现过学习现象,预测模型的网络结构难以确定,同时由于神经网络预测算法在预测过程中收敛速度慢、需要大量的样本数据和推广能力较差等不足,导致这种方法难以在实际工业生产中难以运用。
针对以上出现的磨削去除量控制问题,本文采用了一种基于支持向量机的预测方法,该预测方法根据磨削实验获得的测量数据,选择一组能够通过测量工具进行实时测量的变量,通过支持向量机回归算法建立磨削去除量预测模型,实现对磨削去除量的预测。通过设计单因素实验和交叉实验获得实验数据,并进行回归建模,验证了该方法的可行性。
1 支持向量机原理
1.1 支持向量机(SVM)
随着近几十年机器学习算法的不断深入研究,针对非线性回归的方法不断增加。尤其是文献[5-6]于1995年公布了一种支持向量机(SVM)的分类算法后,众多预测算法被直接应用于解决函数拟合问题[7-8]。支持向量机具有的基于结构风险最小化原则[9],这促成了该方法的泛化能力较强,同时该方法适用于小样本、多维度、非线性的情况,这些优势让支持向量机与其他机器学习方法例如神经网络等预测算法完全不同。
假定U=(xi,yi)(其中,i=1,2,…,n;xi∈Rn,为输入变量;yi∈R,为对应的输出值)为实验得到的实验样本,那么支持向量机的最根本的目标就是通过中得到一个划分超平面(w,b),将分属于相同类别的样本划归到一侧,而将属于其他类别的样本划归到其他空间中。在在由训练样本集U所构成的多维空间中,超平面的划分可以经过下面的线性方程进行表达:
wTxi+b=0
(1)
其中,超平面的垂直法向是通过w=(w1,w2,…,wd)来直接确定的;b为位移项,它表示的是划分超平面到样本点之间的垂直距离。样本空间中任意的样本点x到超平面(w,b)的距离假定为r,其表达式为:
(2)

(3)
如图1所示,距离超平面最近的训练样本点被定义为支持向量(supportvector),这些样本点令式(3)的等号成立,两个被划分到不同类别的支持向量到超平面的垂直距离之和为:

图1 支持向量机与间隔
(4)
其中,r被称为“间隔”(margin)。

(5)
当空间样本集能够全部被划分超平面正确分类,那么所求的最大间隔被称为硬间隔;如果我们允许少数的样本点没有被划分超平面正确分类,就称所求的最大间隔为软间隔。为了提高分类的准确度的同时,保证所建立的模型不会出现过学习的情况,提高模型的泛化能力,因此,引入了松弛变量ξ和惩罚系数C。当惩罚系数C过大时,对出现错误分类的情况的惩罚就会增大,反之,对错误分类的情况的惩罚就会减少。引入松弛变量和惩罚系数后,最大间隔问题转化为优化问题:
(6)
(7)
通过选择合适的松弛变量ξ和惩罚系数C,来实现最大程度的正确分类空间样本,同时还不会导致过学习的情况发生。这就是支持向量机的原理。
1.2 支持向量回归机(SVR)
为了更好地判断支持向量机的优劣,引入了损失函数,损失越大则说明该支持向量机的分类能力越差。对于分类来说,那些分布在间隔内的空间样本点,即被错误分类的空间样本点将会被计算进损失;而对于回归而言则恰恰相反,是将分布在间隔以外的样本点计算进损失,以达到回归的目的。
而针对非线性回归问题必须要用到非线性映射方法,数据xi是通过一个非线性映射Φ将其映射到了高维度特征空间R,然后再对其开展非线性回归,并在特征空间中利用核函数替代线性问题中的内积运算,即:
K(xi,xj)=φ(xi)φ(xj)
(8)
最后得到支持向量机拟合函数为:
(9)

2 基于SVR建立磨削去除量预测模型
磨削去除量主要与工件材料及其材料属性、工件表面曲率、工件进给速度、砂带型号及粒度、砂带线速度、砂带磨损程度、磨削力大小等因素相关因此针对某一材料的工件,其磨削去除量的特性参数可表示为:
F(x)=f(r0,v0,v,c,m,f)
(10)
式中,F为磨削去除量;r0为工件表面曲率;v为工件进给速度;v0为砂带线速度;c为砂带型号及粒度;m为砂带磨损程度;f为磨削力。
目前,由于还没有较为成熟的参数选定方法,惩罚系数C和不敏感损失函数e,只能根据经验来确定其初始值,然后使用网络搜索和交叉验证的方法来寻找最优的参数值。对于核函数K,目前被广泛应用于回归预测的核函数类型主要包括有:线性核函数、多项式核函数、径向基核函数(RBF)以及sigmoid核函数。由于径向基核函数(RBF)无论是在低维度,又或者是高维度,小样本,亦或者是大样本等多种情况下都有很好的表现,同时该核函数具有较宽的收敛域,是目前被广泛应用的核函数。因此也采用了RBF核函数来作为支持向量机的核函数:
(11)
3 磨削实验数据获取与建模结果分析
3.1 磨削实验配置与实验数据获取
为了验证建立的预测模型是否能够准确地预测磨削去除量,因此我们通过搭建合理的磨削去除量采集系统来获得实验数据,磨削去除量采集系统有以下几个部分构成:工业机器人、砂带磨削设备、六维力传感器、LVDT位移传感器、PC电脑端。由于工件体型较小、较轻,因此我们采用工业机器人夹持工件的方式,在磨削设备上进行磨削加工,同时工业机器人的端部安装有六维力传感器来实现磨削加工过程中的磨削力大小的采集,六维力传感器将测得的磨削力实时传输并记录到PC电脑端;磨削设备可以实现对砂带线速度的调节,并将砂带线速度实时传输和记录到PC电脑端;每次完成磨削加工后,通过LVDT位移传感器对由工业机器人夹持的工件进行测量,以获得磨削去除量,并将测量得到的磨削去除量传输和记录到PC电脑端。磨削去除量实验数据采集系统如图2、图3所示。

图2 磨削去除量采集系统示意图

(a) 磨削设备 (b) 上位机
我们以砂带粒度、砂带线速度、砂带磨损程度、工件曲率、工件进给速度以及磨削力为磨削加工工艺参数,以磨削去除量为测量结果,并利用搭建的磨削去除量采集系统进行实验数据采集实验。
采用的工件材料为Cu,采用的砂带为堆积型CSi材料,接触轮的直径为400 mm,接触轮的弹性模量为0.349 46,表1即为我们实验得到的实验数据。
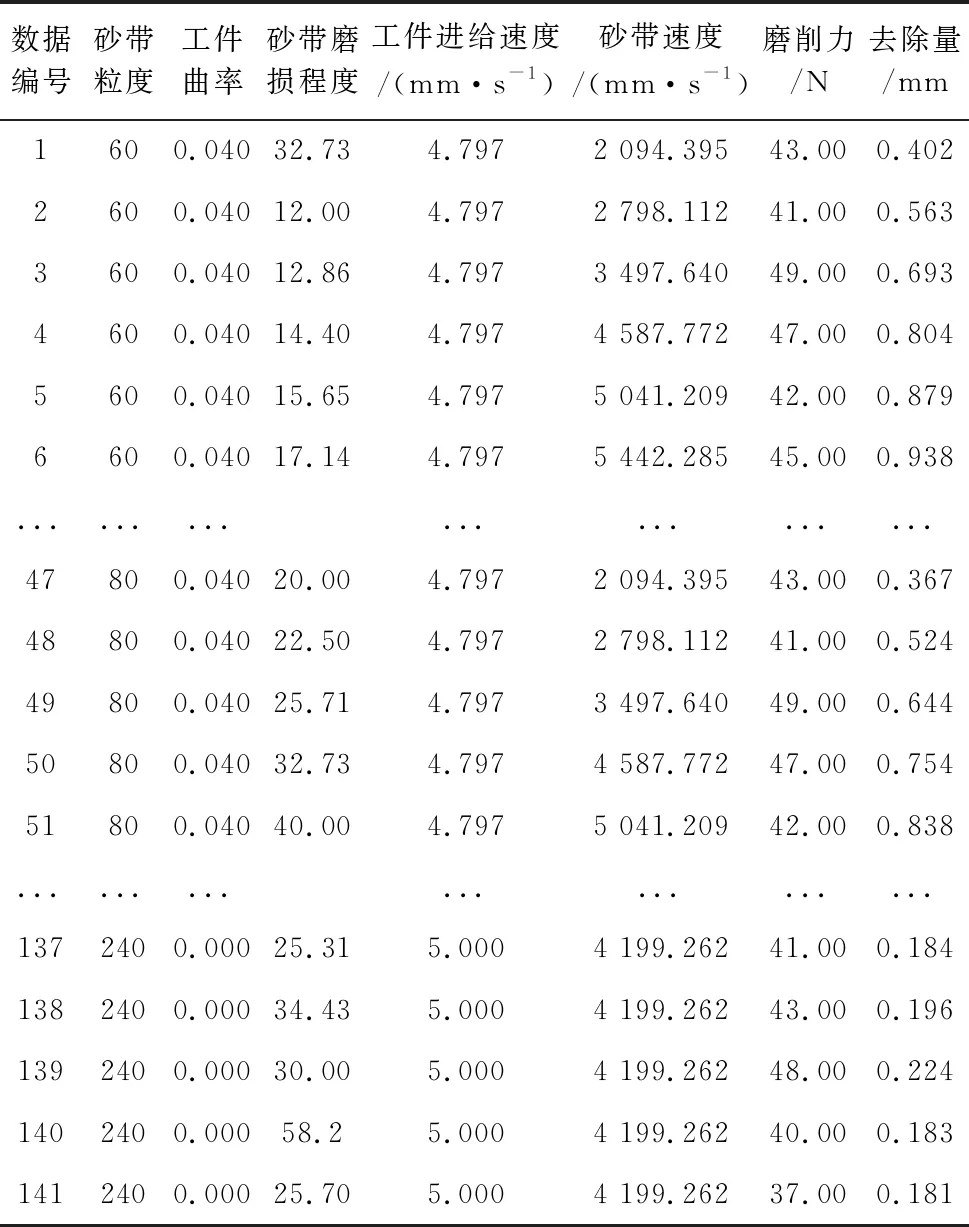
表1 磨削去除量实验数据集
3.2 实验结果与分析
为了验证我们获得的实验数据是否合理,我们通过对实验数据的单因素分析可得出以下结果:
图4展示了磨削力、进给速度、砂带线速度、工件曲率、砂带粒度等各因素对磨削去除量的影响,根据实验数据以及每个因素对磨削去除量的影响曲线分析,充分说明选择的样本特征是基本符合磨削理论的。
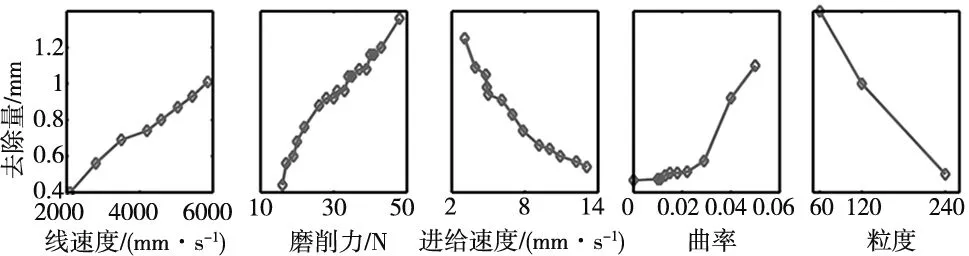
图4 各因素对磨削去除量的影响
为了验证建立的预测模型是否正确,我们利用建立的SVR回归预测模型对实验获得的磨削去除量实验数据进行了训练和预测,图5为经过支持向量回归机(SVR)训练得到的训练结果及误差,图6为经过支持向量回归机(SVR)对测试机进行测试和预测得到的结果及误差。可见预测模型的泛化能力较强,预测误差较小。

图5 训练结果及误差(SVR)
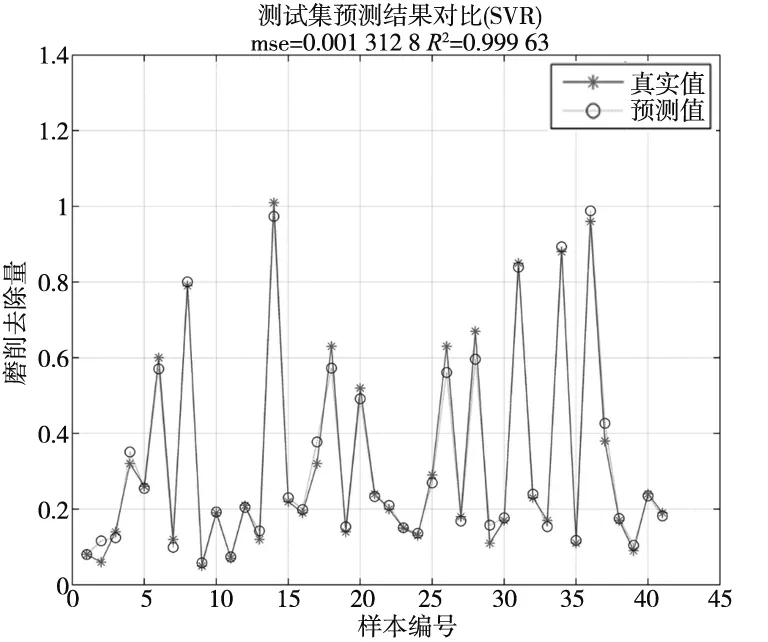
图6 测试结果及误差(SVR)
本文中所建立的回归模型与文献[10]中所使用的BP神经网络回归模型对测试样本集的预测结果比较结果如图7所示,由此可知,相较于BP神经网络回归模型,利用支持向量回归机所建立的回归模型的预测误差更小、准确度更高。

图7 测试结果及误差(BP神经网络)
4 结论
(1)通过MATLAB采用支持向量回归机(SVR)对磨削去除量进行训练和预测,收到了很好的预测结果,预测值相比与实验值的精度为99.963%,预测结果的均方误差为0.131 28%,完全能够满足实际的预测要求。
(2)通过针对性地研究对磨削去除量影响较大的几个因素—砂带线速度、工件曲率、工件进给速度、砂带粒度、砂带磨损程度以及磨削力大小,并将这些主要因素作为预测模型的输入量,以磨削去除量作为输出量,利用实验获得的样本数据进行训练和预测,能够很好地解决磨削去除量无法实时获取的难题,同时该回归模型的预测精度达到了磨削加工的基本需求。
(3)通过对比支持向量回归机(SVR)和BP神经网络两种预测方法对磨削去除量的预测结果可以发现:在针对小样本、多维度的模型预测时,支持向量回归机能够更准确地进行预测。

