重型AT主调压系统油压动态特性优化研究*

董 勇，吴怀超，穆俊齐，彭 昭，曹 刚

(贵州大学机械工程学院，贵阳 550025)

0 引言

重型液力自动变速器因其优越的连续动力换挡和自动调节能力，广泛应用于重型汽车、工程机械以及特种车辆等领域[1]。主调压系统作为重型液力自动变速器液压系统的核心液压子模块，其阀体结构参数对主调压系统的油压动态特性有着决定性的影响，若设计阀体结构参数不当，会导致输出油压过大或输出油压不稳定，进而影响换挡品质及其工作寿命[2]。因此，针对重型液力自动变速器的油压自动调控以及换挡品质控制需求，对影响主调压系统输出油压动态特性参数进行合理的设计及优化是研究关键点。

近年来，国内外众多学者对主调压系统展开了研究。文献[3]以HD4070PR自动变速主调压阀结构参数为切入点，对其进行了静态分析。文献[4]分析了某型液力自动变速器不同档位下主调压系统输出稳态主油压。文献[5]在分析调压阀动态特性基础上，运用所提出的非线性解析法有效预测出了该系统的动态响应。上述研究均取得了一定的研究成果，然而以上研究都是从较小功率自动变速器的单个调压阀展开研究，针对重载型自动变速器鲜有学者从主调压阀和控制压力调节阀结构参数对主调压系统的输出油压动态特性影响展开研究。

本文以某型重型液力自动变速器为对象(可实现1个空档、7个前进档和1个倒档的动力输出)，展开重型液力自动变速器主调压系统阀体结构参数对其输出油压动态特性的影响研究，并采用粒子群算法和遗传算法，对影响主调压系统油压特性的阀体结构参数进行优化设计。

1 主调压系统工作原理

主调压系统自动调控整个液压系统的压力与流量，如图1所示，液压泵加压后油液作用于主调压阀，当供给油压不足以克服弹簧预紧力时阀芯处于最上端位置，泄油口被关闭；而当供给油压持续增大，自反馈油压pm1相应增大，主调压阀阀芯便在液动力作用下克服弹簧预紧力下移，泄油口打开，并在电磁阀反馈压力pd、变矩器反馈压力pT以及锁止阀反馈压力pLC1下实现溢流作用下输出主油压pm。同样地，当压力pc1逐渐增大到足以克服控制压力调节阀的弹簧复位力时，控制压力调节阀阀芯下移，实现二次减压作用，输出稳定控制油压pc。

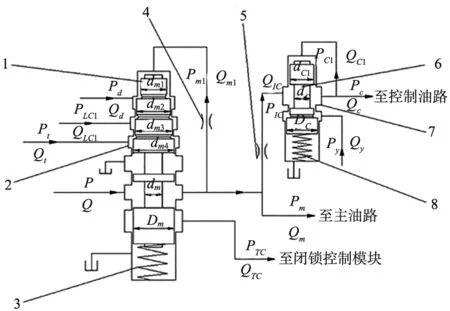
1.主调压阀阀芯 2、7.阀体 3.主调压阀复位弹簧 4.阻尼孔1 5.阻尼孔2 6.控制压力调节阀阀芯 8.换挡阀复位弹簧

2 主调压系统的数学模型

根据对主调压系统的工作原理分析，可建立主调压系统的数学模型为：

(1)主调压阀与控制压力调节阀可描述为质量弹簧阻尼系统，忽略库伦摩擦力的影响，则可建立阀芯的动力学平衡方程为：

(1)

式中，Sm1～Sm4分别为主调压阀的反馈压力pm1、pd、pT以及pLC1的有效作用面积；Mm、Mc为阀芯质量；Cm、Cc为阀芯粘性阻尼系数；Kd、Kc为弹簧刚度系数；xm、xc为阀芯位移；xm0、xc0为弹簧预压缩量；Fms、Fcs为阀芯瞬态液动力；Fmw、Fcw为阀芯的稳态液动力。

(2)主调压阀和控制压力调节阀自反馈腔室的流量连续性方程：

(2)

式中，βe为油液等效体积弹性模量；Vm1、Vc1分别为主调压阀和控制压力调节阀自反馈压力腔室容积；Co是阻尼孔流量系数；do1为阻尼孔1直径。

3 主调压系统的仿真分析

基于上述分析，运用AMESim仿真平台搭建其仿真模型，如图2所示，主调压系统的建模参数见表1。仿真过程中不考虑油液泄露的影响，假设温度恒定，且为模拟主调压系统的自动调控工作过程，仿真重型液力自动变速器4个不同的档位。时间设置：0～4 s为倒挡；4～8 s为Ⅰ档；8～12 s为Ⅴ挡；8～16 s为Ⅶ档。

1.油液属性 2.液压泵 3.主过滤器 4.安全阀 5.主调压阀 6.控制压力调节阀 7.阻尼孔1 8.阻尼孔2

表1 主调系统建模主要参数表

通过将各级反馈油压引到主调压阀的各反馈压力腔室，得到主油压pm如图3a所示，倒档主油压pm约为20.5 bar；Ⅰ档时，主油压pm调控为18.2 bar；Ⅴ档时，主油压pm再调控为14.4 bar；Ⅶ档时主油压pm最终调控为13.7 bar。同时，还由图3b看出，控制压力调节阀输出油压pc在0～2.9 s内存在超调量，波动较为剧烈，在2.9 s后控制油压值稳定在10.64 bar附近。各档位主油压pm最优范围分别为：空档和倒档：18～20.8 bar；Ⅰ档～Ⅱ档：13～17 bar；Ⅲ档～Ⅶ档：6.8～13 bar[2]；此外，控制压力调节阀的初期输出油压特性较差，波动十分显著，超调量大。这会造成摩擦结合元件的疲劳磨损和换挡冲击，影响重型液力自动变速器的实用寿命。

(a) 主调压阀输出油压特性

为此，需对所设计的主调压阀和控制压力调节阀的几何结构参数进行修正，以提高重型液力自动变速器的换挡品质、乘坐的舒适性和实用性。

4 主调压系统输出油压特性影响因素分析

为确定相关主调压阀与控制压力调节阀几何结构参数对主调压系统输出油压动态特性的影响，从主调压阀阀芯直径dm3、控制压力调节阀的初始遮盖量ulc与弹簧刚度Kc分别进行主调压系统输出油压的动态特性仿真分析。

(1)主调压阀阀芯直径dm3

由图4a仿真结果可以看出，若减小阀芯直径dm3，则主调压阀输出主油压pm会增大；适当增加阀芯直径能有效降低Ⅴ档和Ⅶ档时主油压pm，这与理论分析结果一致。然而，Ⅰ档工况下主油压pm未能有效降低，这是由于在初始设定值下(即dm3=21.2 mm时)，在自反馈压力pm1、反馈压力pd和反馈压力pLC1作用下主调压阀阀芯已运动至最大位移量处，继续增大反馈压力pLC1的有效作用面积，不会改变进出油口过流面积，进而无法再调控主油压。

(2)控制压力调节阀初始遮盖量ulc

为确定不同形式初始遮盖量对控制压力调节阀输出油压特性的影响，如图4b所示。不同的预开口量对控制压力调节阀输出油压特性有着显著地影响，其中负遮盖量的动态响应特性较差，最大超调油压达到13.7 bar；正遮盖量降低了控制油压的波动，但又一定程度地降低了控制压力调节阀的二次减压功用，初始设定遮盖量的控制压力调节阀性能介于负遮盖量和正遮盖量之间。

(3)控制压力调节阀弹簧刚度Kc

由式(1)的控制压力调节阀动力学平衡方程可知，增大控制压力调节阀弹簧刚度Kc会改变阀芯运动平衡。由图4c结果所示，不同弹簧刚度系数Kc会影响控制压力调节阀的动态特性，增大或减小初使设定弹簧刚度系数Kc都会增大其波动峰值，为此所选用弹簧刚度不宜过大和过小。

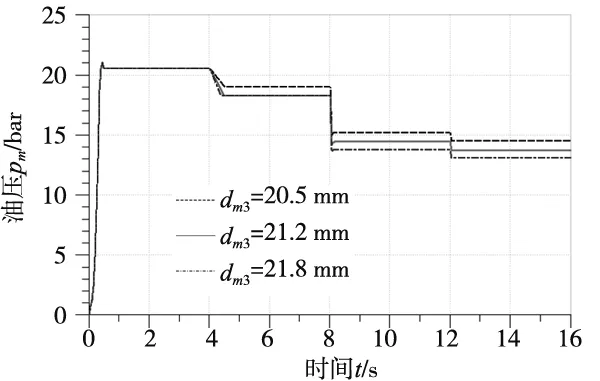
(a) 不同主调压阀阀芯直径dm3输出油压特性

5 主调压系统参数优化

根据前文不同阀体结构参数对主调压系统的输出油压响应特性的仿真分析可知，主调压阀阀芯直径、控制压力调节阀遮盖量和控制压力调节阀弹簧刚度这三个参数对主调压系统的输出油压响应特性均有显著影响。为使主调压系统满足档位所需主油压调控以及输出稳定控制油压得需求，进而达到降低功率损耗、提高重型液力自动变速器换挡性能和实用性的目的，需展开主调压阀与控制压力调节阀的结构参数优化设计。

(1)优化目标函数

对于主调压系统来说关键的是使输出油压快速而准确地调控在最小目标范围内，采用平方误差积分准则(ISE)和时间乘绝对误差积分准则(ITAE)，能兼顾快速响应时间要求和瞬态油压响应误差要求[6-7]。并考虑目标函数的数量级存在差异，归一化处理后的目标函数为：

(3)

(2)设计变量及约束条件

根据前文主调压系统的油压动态因数影响分析，主调压阀阀芯直径dm3、控制压力调节阀初始遮盖量ulc、控制压力调节阀弹簧刚度Kc，这些结构参数对输出油液特性有影响，此外本文还将主调压阀阀芯直径dm4、控制压力调节阀阀芯质量Mc作为优化参数。即可设定主调压系统的设计变量为：

α=[dm3dm4ulcKcMc]T

(4)

各参数优化设计及约束范围见表2。

表2 优化设计及约束参数表

粒子群优化算法(PSO)作为一种实用性较强的优化算法，具有连续性强和收敛速度快的特点；而遗传算法(GA)具有内在隐并行性和全局选优能力，它们均适用于多目标参数优化设计[8-10]。因此，为寻优化设计及约束范围内最优解，分别运用PSO算法和GA算法进行参数优化对比。

考虑到优化设计参数间的相互交互作用，可采用包含交叉项的完全二阶响应面模型，拟合数学模型为：

(5)

式中，J为目标函数，xi为优化设计参数变量，βi为待定系数，ε为误差。

目标函数与优化设计参数间的拟合优度为[11]：

(6)

基于PSO算法的优化过程，设定PSO算法属性为：种群规模为200，最大进化次数为100，学习因子C1=C2=2。优化结果具体见表3。

GA优化算法研究中，设定算法属性为：种群规模为30，复制率为60%，执行的终止遗传代数为20，变异率10%，变异幅值为0.5。优化完毕后优化结果，具体如表3所示。

表3 优化结果

由图5a主调压阀输出油压特性优化结果可看出，8～12 s内(Ⅴ档)在各级反馈压力的作用下，主油压较优化前降低了约2.4 bar；12～16 s内为Ⅶ档时重新调控为11.3 bar，即经过优化后的设计参数将主油压调控在了最优目标范围内；根据图5(b)的控制压力调节阀输出油压特性，在PSO优化算法下达到稳态油压时间、震荡衰减次数和超调量分别为tp=3.75 s 、5次和14%，而GA算法下达到稳态油压时间tG=2.3 s，控制油压衰减震荡次数为3，超调量为14%。这两种优化算法中，PSO算法注重快速性，即达到稳态控制油压的响应时间更短；而遗传算法下的油压的稳定性的却更具优势，这主要表现在控制油压的震荡衰减次数和超调量。

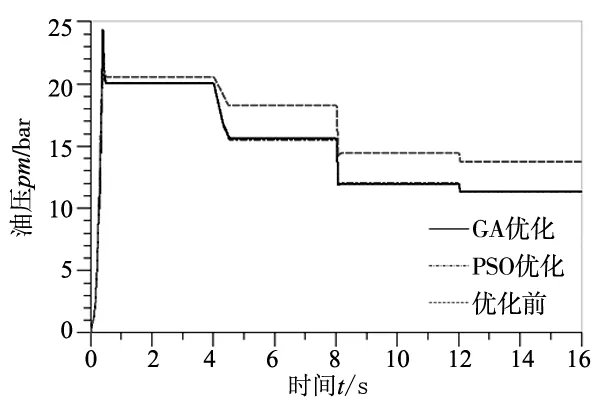
(a) 主调压阀输出油压特性

6 结束语

通过对重型液力自动变速器主调压系统工作原理分析，在建立调压阀数学模型的基础上，展开油压动态特性影响分析与优化：

(1)主调压阀阀芯直径、控制压力调节阀初始遮盖量与控制压力调节阀弹簧刚度3个关键结构参数显著影响主调压系统的输出油压特性。

(2)基于POS优化算法与GA优化算法对主调压系统的结构参数进行优化，优化缩短了稳态油压响应时间、减少了震荡衰减次数，也降低了超调量，进而显著改善了主调压系统输出油压特性，验证了所建立模型和优化设计的正确性。为后续重型液力自动变速器液压系统回路设计和性能优化研究奠定了基础。