一种双框架振动陀螺的接口电路仿真及实验

刘 恒，杨添熠，舒进华，张 玉，苏 伟

(1.南京信息工程大学电子与信息工程学院，江苏南京 210044；2.中国工程物理研究院电子工程研究所，四川绵阳 621900 )

0 引言

微机械框架式振动陀螺模态谐振频率和品质因数随环境温度波动，模态的动力学参数亦随温度缓慢变化，从而陀螺输出发生漂移[1]。抑制温漂主要从材料选择、微结构设计(拓扑结构和温度补偿结构)、封装、测控电路及信号处理来展开[2-3]。微结构的制造依赖于工艺流程，考虑到接口电路的工艺兼容性，掺杂的硅材料是微机械振动陀螺的结构层主要材料。微结构的创新设计和额外的温度补偿微结构设计均需重新分析结构的动力学和振型的稳定性等。微结构流片封装后，测控电路影响着微机械陀螺的性能[4-5]。微机械振动陀螺属于典型的微机械谐振式传感器，在模拟驱动控制中，有锁相环频率跟踪和自激振荡驱动2种方案[6-8]。文中设计了一种双框架解耦微机械振动陀螺，并分析了其动力学原理，并利用体硅溶片工艺制造了陀螺表芯，利用金属管壳储能焊真空封装，建立了陀螺自激振荡和自动增益控制分析模型，由于系统的高阶弱非线性，采用平均周期法分析了系统的稳态行为及稳定条件。根据设计版图和开环测试参数，建立了基于MATLAB/Simulink的数值仿真模型，仿真验证了理论分析结论的正确性。硬件实验测试表明测控电路的动力学原理与理论分析一致，制造的微机械振动陀螺在测控电路的驱动下，短时间内具有较好的振动频率和振动幅度的稳定性，为后续微机械陀螺输出漂移抑制提供了理论和实验依据。

1 微机械双框架解耦振动陀螺

微机械振动陀螺表芯包括结构层和电极层。结构层包括4个支撑框架的框架锚点，4个检测模态折叠梁分别与框架锚点连接并悬空。外框架质量块在检测模态折叠梁的支撑下也悬空，外框架质量块的左右两侧分布有极板，极板均分为上下两部分。外框架左右两侧布置有对称的检测极板，检测极板在检测锚点的支撑下悬空，每侧的极板与对应的外框架极板构成检测电容，其中每侧的2组检测电容构成差分电容对。左右两侧对称增大了检测模态的输出信号[9]。

为防止传感器折叠梁断裂失效[10]，在内框架质量块外侧有突出的止档板。结构层见图1。电极层引出7个电极引线与封装管脚连接，检测模态2个电极引线构成差分检测，驱动模态对应的驱动梳齿和驱动检测梳齿各2个电极引线，框架连接锚点引出1个电极引线。

图1 微机械双框架振动陀螺结构图

微结构采用单晶硅，掺杂浓硼改变导电性，衬底材料为7740玻璃，微机构与衬底键合。为得到较大的深宽比，用ICP深硅刻蚀工艺。工艺流程：第1步，将清洗单晶硅硅片后刻蚀出键合台；第2步，扩散掺杂浓硼，增加结构的导电性；第3步，在硼硅玻璃上溅射金然后光刻出电极和引线；第4步，将玻璃和硅用阳极键合技术进行键合；第5步，将键合后的硅片背面用干法刻蚀多余硅，将结构层减薄；第6步，硅片背面用深硅刻蚀工艺刻蚀出微结构。工艺流程成品率高，结构与衬底间的间隙易控制，污染杂质少，工艺流程相对简单，成本低。工艺流程见图2，微陀螺扫描电镜照片见图3。

图2 体硅工艺流程

图3 微机械双框架振动陀螺电镜照片

差分驱动电压作用于驱动模态的驱动梳齿上，内框架沿X轴左右振动，通过驱动模态的检测梳齿来判断外框架是否处在恒幅谐振。当Z轴存在角加速度Ω时，外框架受到沿Y轴方向的科氏力，检测模态的检测极板构成的差分电容发生变化，通过接口电路将电容变化转换为电压变化再去解调就得到Z轴方向的角加速度，动力学方程为：

(1)

(2)

式中：mx、my和Fx、Fy分别为驱动模态和检测模态的质量和外部驱动力；mc为科氏力方向的等效质量；cx、cy和kx、ky为驱动模态和检测模态的阻尼系数和折叠梁的等效刚度；x(t)、y(t)分别是模态对应的框架位移，对时间求导就是对应的速度和加速度。

根据式(2)，驱动模态的框架速度耦合角加速度和质量就成为科氏力，驱动模态和检测模态存在一定的频差，检测模态处在开环受迫振动，Fy为0。同时，驱动模态框架谐振时，驱动力远大于科氏力，忽略科氏力对驱动模态位移的影响[11]。求解式(1)和式(2)，得到框架振动位移的稳态表达式：

(3)

(4)

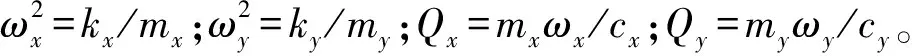
要使检测信号幅度最大，驱动力频率应等于驱动模态的谐振频率，使驱动模态振动幅值最大。检测模态的谐振频率也与驱动信号的频率一致[12]，即ωx=ωy=ωd。模态位移可化简为：

(5)

(6)

机械灵敏度δ为

(7)

根据式(5)～式(7)，当驱动电路保持驱动框架谐振并振幅恒定时，检测模态的位移最大。增大振幅Ad和检测模态的Qy及减小驱动模态频率ωx可提高灵敏度δ。

微机械振动陀螺的驱动和检测方式有多种，在静电方式中，主要通过平板电容和梳齿电容来实现驱动和检测。陀螺检测采用差分平板电容对，检测电容CS1和CS2及差分检测电容CS为：

(8)

(9)

(10)

式中：n1为平板电容对数量；ε为介电常数；Sy为平板正对面积；d0为极板间距。

式(10)表明差分检测电容大小与检测模态位移具有线性关系。

内框架采用静电梳齿结构驱动和检测，驱动模态的检测梳齿电容CDS(t)为

(11)

式中：n2为检测梳齿电容对数量；l为初始梳齿交叠长度；h为梳齿的厚度；d1为活动梳齿和固定梳齿间距。

式(11)表明驱动模态的检测梳齿电容大小与框架位移x(t)成正比。

差分驱动梳齿对在直流偏置电压Vd与交流电压Vacos(ωdt)共同作用下产生静电驱动力Fx(t)：

(12)

式中：n3为驱动梳齿电容对数量；d2为驱动活动梳齿和固定梳齿间距。

2 驱动模态自激振荡控制

研制的微机械陀螺采用金属管壳真空储能焊封装，品质因数达到1800以上，用自激驱动和自动增益控制来实现恒幅和频率跟踪控制[13]。驱动模态测控电路包括电荷放大器、全通移相器、全波整流器、模拟低通滤波器、反相加法器、比例积分控制器，双向电源供电。测控电路动力学分析模型见图4，系统是高阶非线性的，采用经典控制理论方法难以得到系统的输出响应[14]。

图4 微机械陀螺驱动模态自激振荡控制

假定驱动模态微结构振动位移x(t)为

x(t)=a(t)cos[ωdt+φ(t)]

(13)

式中：a(t)为幅度；相位为φ(t)。

在差分驱动条件下，静电力相位超前位移相位90°，在硬件实现上通过两节运算放大器全通移相器来实现。不同频率全通移相器相位不同，实际两节移相器实现π/2+φ移相，φ为相位偏差，φ∈[-π/2,π/2]。静电驱动力Fx(t)为

Fx(t)=k2·k1a(t)cos[ωdt+φ(t)+π/2+φ]·Vd

=-KVda(t)sin[ωdt+φ(t)+φ]

(14)

式中：k1为电荷放大器的放大系数；k2为驱动梳齿的电压-力转换系数；K=k1·k2。

根据各模块的动力学原理，建立分析模型，有：

(15)

(16)

(17)

(18)

(19)

(20)

状态方程特征矩阵为

求解矩阵的特征值λ,有:

(21)

根据劳思判据，驱动模态振动稳定需满足：

(22)

通过改变kp、kI及τ可实现系统具有不同的极点和不同的动态性能。根据式(17)，驱动模态稳态振幅a(t)与VR、k1有关，与微结构的刚度、质量、谐振频率与品质因数无关，在温度扰动下，频率漂移对应的闭环驱动模态振幅保持不变，能实现恒幅振动和频率跟踪。

(23)

求解不等式(23)后，有：

(24)

根据式(24)，VR必须大于静态平衡点对应的直流驱动电压，驱动模态微结构能稳定起振。移相误差φ在理想条件下应为0，当存在相位偏移时，偏差角度越大，则需更大的VR才可起振。

3 微机械陀螺驱动模态的数值仿真

为了对平均周期法定量分析的微机械振动陀螺的驱动模态测控电路进行验证，在MATLAB/Simulink下建立数值仿真模型。微结构参数根据版图设计确定，封装品质因数由硬件电路开环测试确定，仿真模型见图5，模型参数见表1。微机械陀螺结构材料为硅，硅是一种热敏材料，弹性模量E随温度T变化而变化，硅微结构的刚度k与温度T的关系为[2]：

k=k0-CE·k0(T-T0)

(25)

式中：CE为弹性模量E的温度系数；k0为温度为T0时的机械刚度。

图5 微机械振动陀螺驱动模态仿真模型

表1 传感器及测控电路参数

为验证自激振荡对频率跟踪和恒幅控制作用，在仿真时间2 s加入54.4 N/m(原始刚度的20%)的阶跃刚度扰动，整个仿真时间为5 s。

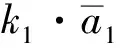
图6 振幅信号(VR=1.0 V)

图7 检测电压A(VR=1.0 V)

图8 驱动电压Vd(VR=1.0 V)

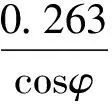
图9 振幅信号(VR=0.5 V)

图10 检测电压A(VR=0.5 V)

图11 驱动电压Vc(VR=0.5 V)

图12 输出无过冲(VR=1.0 V)

图13 输出无过冲(VR=0.5 V)

4 实验测试

流片后的微陀螺采用金属储能焊真空封装，并据自激振荡电路设计PCB并调试。用Agilent35670A开环测量驱动模态的频率响应，直流驱动电压为3 V，交流电压幅值为1 V，频率扫描范围为0～30 kHz，在12～14 kHz范围内得到频率响应曲线，1#陀螺的谐振频率为13.569 kHz，幅频曲线关于谐振点并不对称，测得的阻尼系数换算成品质因数为1891。2#陀螺的谐振频率为13.552 kHz，品质因数为1863。

图14为测控电路的全波整流，图15为全通等幅值移相器，通过滑动变阻器调节移相度数，硬件电路与数值仿真模型动力学原理一致。当式(24)不满足时，微结构无法起振，输出见图16。

图14 全波整流

图15 全通移相

图16 未起振输出

通过调节VR和移相器相位实现驱动模态的闭环谐振，图17是驱动模态起振电压信号，稳态幅度恒定，但不同的陀螺的品质因数和微机构参数有差异，VR不同时得到的输出波形幅值不同。输出信号接入Agilent53132A 数字频率计，在模态频率范围内可分辨10-5Hz，对输出信号频率稳定度进行静态测试，采样间隔为1 s，一次采样3 500个数据，近1 h内采样数据见图18。Allan方差分析得到短期频率稳定度曲线见图19，最大偏差为0.06 Hz，频率稳定度达到±5 ppm。

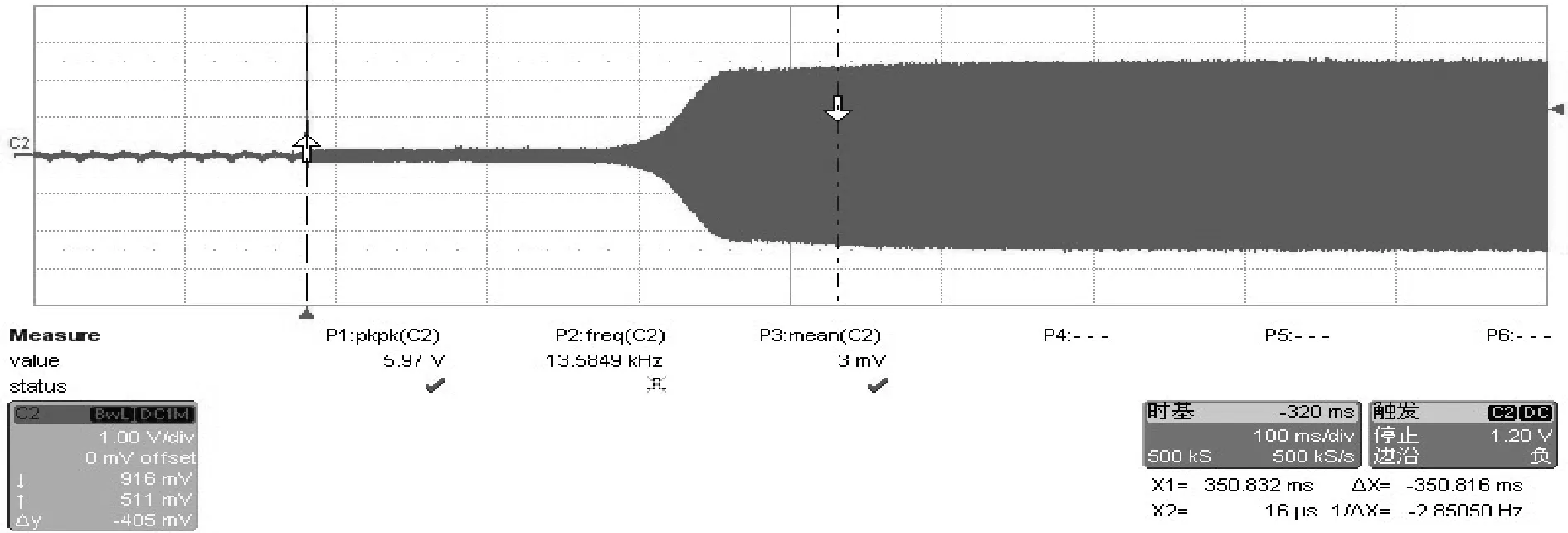
图17 驱动模态微结构谐振输出信号(1#)

图18 谐振频率静态测试

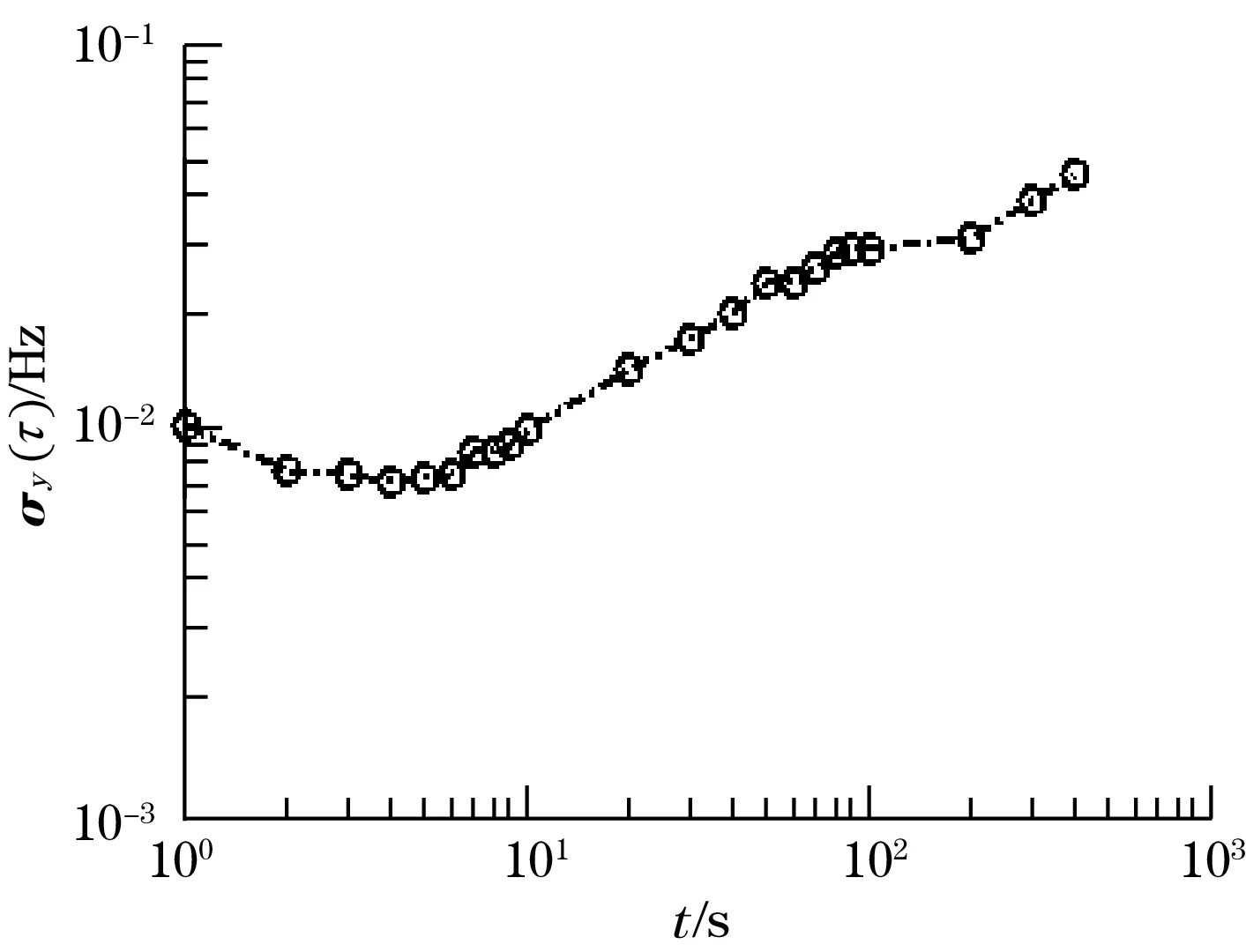
图19 谐振频率偏差

图20 振幅信号幅值

式(17)表明，稳态振幅与直流参考电压和电路放大倍数有关，图17反映了振动幅度的稳定性，上电起振稳定后，振幅在示波器上变化很小。调整直流参考电压大小，利用Agilent34401A和GPIB接口线对输出信号有效值进行采样，采样精度0.05 mV。图20为采样数据，横坐标为采样时刻，单位为s，纵坐标为幅度。对幅度数据进行8 min自动采样，8 min内幅度值漂移0.8 mV，偏差为±0.4%，见图21。分析发现接口电路附近存在交流电压源就存在0.3～0.4 mV的噪声，电路需进一步抑制噪声。

图21 振幅信号幅值偏差

5 结论

分析了一种双框架解耦微机械振动陀螺的动力学原理，推导了陀螺输出表达式，陀螺采用差分梳齿和差分平板电容减小了系统的非线性。针对测控电路对驱动模态的恒幅和频率跟踪要求，近似分析了系统起振条件和稳态平衡点的表达式。数值仿真验证了测控电路稳定性及平衡点的理论分析，平均周期法分析是有效的。流片制造和封装的微机械陀螺系统的测试实验为分析和抑制陀螺输出漂移提供理论和实验基础。