不同预防性维护方式下的两台并行机调度问题

董恩来 谭园园

摘要：在企业实际的生产调度中，设备的维护是不可或缺的。本文以具有不同预防性维护方式的两台并行机调度为研究对象。以最小化最大加工时间为目标建立数学模型，確定工件的加工设备及其加工顺序。将海明距离与自适应步长结合，提出改进的人工鱼群算法，提升算法的性能。最后在不同算例规模的情况下进行仿真实验，并引入遗传算法（GA）作为对照，将AFSA、AFSA-C与GA进行性能对比，其结果表明改进的人工鱼群算法（AFSA-C）性能最优。

关键词：两台并行机;生产调度;预防性维护;人工鱼群算法;组合优化

中图分类号：TP278      文献标识码：A

文章编号：1009-3044（2021）28-0160-04

开放科学（资源服务）标识码（OSID）：

The Scheduling Problem of Two Parallel Machines under Different Preventive Maintenance Methods

DONG En-lai， TAN Yuan-yuan

（School of Artificial Intelligence， Shenyang University of Technology， Shenyang 110870， China）

Abstract： In the actual production scheduling of an enterprise， equipment maintenance is indispensable. This paper takes two parallel machine scheduling with different preventive maintenance methods as the research object. With the goal of minimizing the maximum processing time， a mathematical model is established to determine the processing equipment of the workpiece and its processing sequence. Combining the Hamming distance with the adaptive step size， an improved artificial fish school algorithm is proposed to improve the performance of the algorithm. Finally， a simulation experiment was carried out under different scales of calculation examples， and genetic algorithm （GA） was introduced as a control， and the performance of AFSA， AFSA-C and GA was compared. The results showed the performance of the improved artificial fish school algorithm （AFSA-C） Optimal.

Key words： two parallel machine; production scheduling; preventive maintenance; artificial fish school algorithm; combinatorial optimization

1 引言

调度的产生是由于资源的有限性和稀缺性，有限的资源无法同时满足企业的需求。在实际生产中，企业需要让生产的机器维持高效运转。但是无法避免在运行中出现故障，而导致整个生产计划停滞。此时需要重新调整调度计划或者机器修复完毕才能恢复生产，会耽误一定的时间和增加一定的成本。由此可知，在进行生产调度计划制定过程中，假定设备是一直可以运行的，忽略设备的可靠性、设备的预防性维护是不合理的。需要将预防性维护与生产调度联合起来进行考虑。对这个问题，有很多学者进行了研究。并行机可以看作单机的组合，对于单机调度与预防性维护，马英[1]对单机模型与预防性维护进行了分析，因为维护时长可变可固定，维护时段可变可固定，所以有四种情形。作者对这四种情形进行了分析，提出启发式算法，对最坏情况界进行分析，证明问题的NP难性质。并将求解问题的思路推广到多机系统，验证了所提启发式算法的有效性。Ji M[2]等对单机定周期维护，维护时长为固定值t的问题进行了研究，证明了LPT算法的最坏情况界是2，并且通过证明除非此问题为P=NP的，否则不会存在比LPT更好的算法。在并行机与预防性维护方面，江才林等[3]根据异速并行机的特点，在考虑周期性预防性维护的情况下，提出HGA算法，发现对于大规模问题，HGA算法性能优异。徐德华等[4]人研究了具有周期性维护的并行机问题，并且根据非抢占作业问题，对比了LPT算法和LS算法的优劣。Mosheiov等[5]以无关联并行机调度系统为研究内容，假定所有设备的预防性维护作业需要同时进行，以总完工时间为目标，维护作业的时间窗口为[0， T]，维护时间长度为常数t的模型进行了研究。杨晓霞[6]考虑了平行机系统下的维护计划，对平行机系统中的设备采用同样的维护约束条件，基于贪婪机制进行求解。

针对预防性维护下并行机调度问题研究的特点以及其不足之处，本文考虑具有两台不同维护方式的单机调度组成的并行机系统，以最小化最大加工时间为目标，针对每台设备的维护特点，建立数学模型。决策工件的加工位置和加工顺序。

2 問题描述

有n个独立的工件j1，j2，…，jn安排到两台并行机M1，M2上加工。其中对M1进行工具更换维护，两次相邻的维护之间的最大时间间隔是t1，为柔性周期维护。机器M2进行周期维护，每两次相邻的维护之间的时间间隔事先给定为t2，针对该问题，有下面的几个条件：（1）工件j1， j2， …， jn的加工时长分别是p1， p2， …， pn ;（2）所有的加工工件在加工时都是不可以中断的，并且在零时刻都已到达生产线，到达后可以立即进行工件加工;（3）两台机器在开始加工前都已经完成了一次维护，机器到达生产线后可以马上启动机器对工件进行加工;（4）对于机器M1的维护时间长度w1，设置为固定的正常数，对于机器M2的维护时间长度，设定为与M2加工负载有关的函数w2=F（λ2，j）， 其中λ2，j表示为在机器M2上加工的工件j和上一次维护后的在工件j之前所有已经加工工件的加工时长之和（负载），为非负增加的线性函数;（5）工件的加工时间pj≤max{t1， t2}， j=1，…， n，否则不可加工该工件。

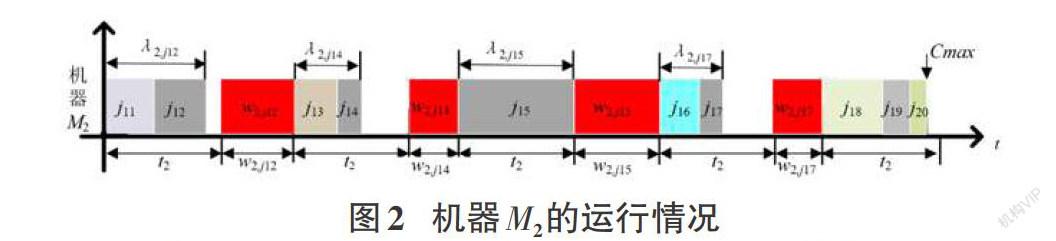
本文考虑以最小化最大加工时间Cmax为目标。本文的决策任务是（1）指派工件的加工设备、确定在同一设备上加工工件的顺序;（2）工件加工的开始时刻与结束时刻;（3）机器M1上维护的开始时刻与结束时刻;（4）机器M2上维护的时长、维护的开始时刻和结束时刻。机器运行情况如下图1、图2所示。

在图1中，t1为最晚开始维护的时间间隔;λ1，j为机器M1上的工件j到上一次维护结束时所有工件加工时间的累加;维护的时长w1为常数。若在加工完工件j之后，机器M1的 λ1，j+ pj+1>t1，则工件j+1不能直接在工件j之后进行加工，需要等维护结束后再进行加工，此时维护可以直接在加工完工件j之后开始。

在图2中，t2为相邻两次维护的时间间隔，为常数;λ2，j为机器M1上的工件j到上一次维护结束时所有工件加工时常求和，也就是负载;维护的时长w2随着负载λ2，j呈非负增加关系。若在加工完工件j之后，机器M2的pj+1+ λ2，j >t2 ，则工件j+1不能直接在工件j之后进行加工，需要等维护结束后再进行加工，此时维护需要等到t2才可开始。

3 模型的建立

3.1参数说明

j ： 工件j的编号，j = 0...n+1;其中j =0 和j = n+1;均表示虚拟工件;pj ：工件j的加工时间;m ： 机器的数量，本问题m=2;i ： 机器的编号， i=1，2;t1 ：机器M1的最大连续加工时间;t2 ：机器M2上相邻两次维护的时间间隔;w1j： 机器M1的维护时间;λi，j ：在机器i上，上一次维护之后到工件j之前加工的工件以及工件的加工时间总和。

3.2 决策变量

sj： 工件j的开始时刻;cj： 工件j的结束时刻;sijm：机器i加工完工件j之后进行维护的开始时刻;cijm：  机器i加工完工件j之后进行维护的结束时刻;w2j ： 机器M2进行维护的维护时间;若工件j分配给机器M1进行加工，不在机器M2上进行加工，则xi，j为1，否则为0;若在机器Mi上，加工完工件j之后，进行维护，则yi，j为1，否则为0;若在机器i上，工件j1 在工件j2 之前加工，则ei，j1，j2为1，否则为0。

3.3 数学模型

针对不同预防性维护方式下的两台并行机调度问题，建立了如下的调度模型：

obj： min Cmax                               （1）

[Cmax=maxnj=1cj]                          （2）

s.t.

[i=12xi，j=1]， j = 1，…，n                         （3）

[j1=0nei，j1，j2=1]， i=1， 2，  [j2=0，…，n]                   （4）

[j2=0n+1ei，j1，j2=1]， i=1，2，  [j1=1，…，n+1]                （5）

[sj2+（3-xi，j1-xi，j2-ei，j1，j2）U-yi，j1wij≥cj1]， i=1，2，  j1，j2 = 1，…，n，  （6）

[w2，j=F（λ2，j）]， j = 1，…，n，                       （7）

[cj=sj+pj]， j = 1，…，n                              （8）

[cmij=smij+wij]， i=1，2，  j = 1，…，n                      （9）

[λi，j≤ti]， i=1，2，  j = 1，…，n                     （10）

[λi，j2=（2-ei，j1，j2-yi，j1）λi，j1+pj2]，  i=1，2，  j = 1，…，n           （11）

其中，式（1）～（2）表示本文研究问题的目标函数。式（3）表示工件只能在一台机器上进行加工。式（4）表示工件有且只有一个前继工件。式（5）表示工件有且只有一个后继工件。式（6）对工件的开始时间进行约束，其中U是一个非常大的正数。式（7）表示机器M2的维护时长和机器M2的维护之后的持续加工时长成函数关系。式（8）表示工件j开始时刻和完成时刻的关系。式（9）表示维护的开始时刻和完成时刻关系。式（10）表示在机器Mi维护后的连续工作时间不能超过最大时间ti。式（11）表示工件j1在工件j2之前加工时，机器Mi的连续工作时间λi，j。

4 算法设计

2002年，李晓磊[7]通过观察鱼类群体的行为活动，提出了人工鱼群算法。人工鱼群算法具有良好的性能，可以用来求解调度问题。

4.1编码与解码

本文采用0-1编码来对机器进行编码，其中，0代表机器M1，1代表机器M2。那么，对于一个包含10个工件的调度问题，其编码方式如下表1所示：

针对本文研究的问题，解码时先根据算法求得的0-1序列，将工件的加工设备确定好，此时工件被分为两组。将分配在机器M1上进行加工的工件，根据先后约束式对工件排序，随后根据上文中图1所示的运行情况，依次将待加工的工件进行判断，决定工件的加工时间与结束时间，最后判断加工此工件后是否进行维护，直到所有分配在此的工件判断并加工完毕，求得机器M1对应的Cmax1;将分配在机器M2上进行加工的工件，根据先后约束式对工件排序，随后根据上文中图2所示的运行情况，依次将待加工的工件进行判断，决定工件的加工时间与结束时间，最后判断加工此工件后是否进行维护，直到所有分配在此的工件判断并加工完毕，求得机器M2对应的Cmax2;最后将Cmax1与Cmax2比较，将较大的那个作为最终结果。

4.2 人工鱼行为

对于一条人工鱼来说，其状态可以用向量X =（x1，x2，x3，…，xn）来表示;人工鱼状态的求解结果用Y = F（X）表示;人工鱼个体之间的距离di，j;Visual表示的是人工鱼的感知范围;Step为人工鱼的最大移动距离，又称步长;δ为拥挤度因子。

觅食行为：由人工鱼此刻的状态及其感知范围。算法会随机选择一个状态，对其进行判断，若其比当前状态优秀，则向其进行随机移动，否则不进行移动。直到达到尝试次数，将移动后的状态进行记录。

聚群行为：由人工鱼此刻的状态及其感知范围。判断其附近人工鱼的数量。计算其中心状态，若中心状态较优，则根据此状态的方位进行随机移动，否则，不移动，执行其他行为。将移动后的状态进行记录。

追尾行为：由人工鱼此刻的状态，判断其感知范围内人工鱼的数量。随后计算附近人工鱼对应的状态，选择其中的最优状态。若此状态比人工鱼此刻的状态优秀，就根据此状态的方位进行随机移动，否则不进行移动。将移动后的状态进行记录。

上述三种行为，本文选择直接对编码进行上述操作，根据不同编码的位数不同，进行相应的改进，来达到人工鱼的移动效果。进行上述三种行为后，需要进行行为评价，从上述行为中挑选移动之后的最优状态，作为最终的移动状态。

公告牌：公告牌是记录鱼群中最优个体的。在迭代中，每条人工鱼都会进行一次寻优，随后将寻优结果与公告牌进行比对。若比公告牌优秀，则进行公告牌的刷新，否则，不进行更改。这是进行算法寻优的必须操作，直到鱼群中的所有鱼都完成一次刷新，才开始进行下一轮迭代。

4.3 自适应步长

针对本文所采用的编码方式，选择采用海明距离来对不同人工鱼之间的距离进行求解。海明距离又被称为码距。可以有效衡量本文编码所确定的人工鱼状态之间的接近程度。若其差距大，则距离就大，此时应该对步长进行适当增大的处理，才能让不同状态之间较快的相互靠近。若其差距小，则距离就小，此时相应的步长可以适当减小，避免在极值点附近发生震荡，导致算法性能减弱。

本文选择将距离与步长进行相等处理，由于不同的人工鱼均是在其视野范围内发现的，所以符合最长步长小于视野的约束條件。此时设此刻人工鱼的状态为Xi。若在其视野范围内存在人工鱼Xj，使得对应的食物浓度Yj比Yi优秀，则计算出Xi与Xj之间的海明距离di，j ，根据海明距离di，j计算人工鱼Xi的移动距离，公式如下：

[Step=di，j]                                             （12）

[Xi|next=Xi+Step·Random]            （13）

由上式可知，将步长与距离进行统一，可以将公式化简，算法也就进行了相应的简化处理。

5 仿真实验

本文采用遗传算法作为改进的人工鱼群的对比算法，遗传算法的编码、解码与种群大小及其初始化的操作与人工鱼群保持一致。交叉方式选择两点交叉，将染色体分为三部分，随后把不同染色体的后两部分分别进行交叉操作。单点变异方式。采用轮盘赌为最优个体的选择方式。

本次实验主要对改进的人工鱼群算法（AFSA-C）、人工鱼群算法（AFSA）与遗传算法GA进行性能比较，主要有三个维度，分别是算法的运行结果、算法停止迭代的次数与算法的运行时间。对上述的算法采用JAVA语言进行编程实现，程序的运行环境保持一致。对算法设置参数如下：AFSA-C的鱼群大小为50，迭代次数为500次，拥挤度因子为45，尝试次数设置为3，视野为10。AFSA的步长设置为5，其他参数与AFSA-C相同。GA的种群大小为50，迭代次数为500，交叉概率为0.6，变异概率为0.2。研究的调度问题工件数n分别为n = 20，n = 50，n = 100，n = 200，n=500，n = 1000。

本文认为迭代停止的条件：算法最后输出的结果在第几代不再变化，就认为算法在该代已经停止迭代。其对比结果如下：

由图3与图4可以看出，在算法的运行时间方面，改进的人工鱼群算法所需时长最短，算法运行效率较高。

由图5图6以看出，在算法迭代停止的次数方面，改进的人工鱼群算法的停止迭代次数最低，证明该算法在初期就在很短的时间内的收敛到最优值附近，收敛效果很棒。

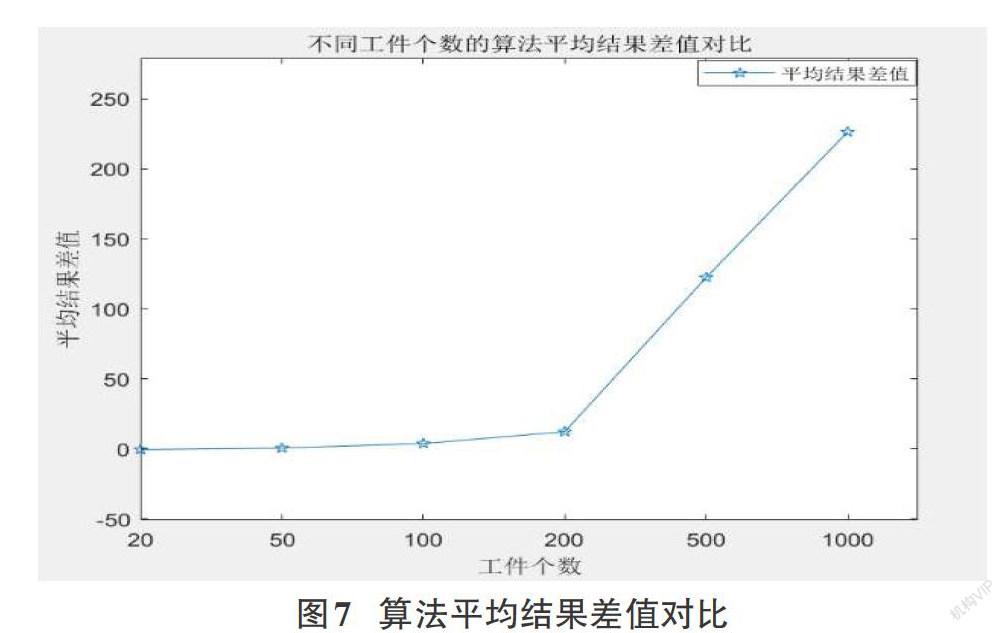
由上图7可知，随着问题规模的扩大，即工件数量的增加，AFSA与AFSA-C二者的差值越来越大，由此可见，在求解精度方面，改进的人工鱼群算法明显占有优势。所以在求解大规模的问题是，可以采用本文所改进的人工鱼群算法来进行求解，以获得更好的效果。

6 总结

本文考虑不同预防性维护方式下的两台并行机调度问题，建立相应的数学模型，针对人工鱼群算法的不足之处，设计了自适应步长的方式进行改进，通过实验对比分析，本文改进的人工鱼群算法，在算法运行时间、算法迭代停止的次数与算法的运行的结果方面具有显著优势。并且随着问题规模的扩大，算法的性能优势更加明显，是一种有效求解不同类型预防性维护下的两台并行机调度问题的方法。

参考文献：

[1] 马英.考虑维护时间的机器调度问题研究[D].合肥：合肥工业大学，2010.

[2] Ji M，He Y，Cheng T C E.Single-machine scheduling with periodic maintenance to minimize makespan[J].Computers & Operations Research，2007，34（6）：1764-1770.

[3] 江才林，陆志强，崔维伟.考虑周期预防性维护的异速并行机集成调度研究[J].哈尔滨工程大学学报，2014，35（11）：1409-1414，1421.

[4] Xu D H，Sun K B，Li H X.Parallel machine scheduling with almost periodic maintenance and non-preemptive jobs to minimize makespan[J].Computers & Operations Research，2008，35（4）：1344-1349.

[5] Mosheiov G，Sarig A.A note：Simple heuristics for scheduling a maintenance activity on unrelated machines[J].Computers & Operations Research，2009，36（10）：2759-2762.

[6] 杨晓霞.考虑设备维护的平行机调度应用研究[D].重庆：重庆大学，2018.

[7] 李晓磊.一种新型的智能优化方法-人工鱼群算法[D].杭州：浙江大學，2003.

【通联编辑：梁书】