公路波纹钢板拱桥内壁应变及外壁土压力测试分析

潘小虎，何 强 ，胡 滨

（1.中交第一公路勘察设计研究院有限公司，陕西 西安 710075；2.西安工业大学，陕西 西安 710021；3.西安中交土木科技有限公司，陕西 西安 710075）

引言

波纹钢板桥涵相比混凝土桥梁，具有节约建筑用料、造价低、节省工期、便于保通的优势[1-3]。通常用于替代临时或永久性道路桥梁，使用镀锌钢板可防止结构中金属结构的锈蚀和腐蚀，降低维修时费用，应用前景较为广阔[4-6]。我国一些科研机构和高校对波纹钢结构涵洞研究的较多，但对于波纹钢拱桥研究较少，尤其是对波纹钢结构的力学特征报道偏少[7-9]。

1 波纹钢板拱桥现场试验方案

1.1 基本概况

依托工程为跨径10 m的钢波纹板拱桥，国内对此方面的受力性能研究较少，属于新型结构。波纹钢板拱桥为波形钢板拼装而成的半圆拱结构，采用Q355钢材，相比混凝土具有施工简易快捷，不受天气和气温影响的优势。通过野外现场试验，测试在施工过程中拱桥内壁应变和外壁土压力的数值，将其应变值和土压力值进行理论分析，最终得出相应规律与结论。

1.2 波纹钢板拱桥内壁应变测试方案

不同填土高度下，测试波纹钢板拱桥不同位置的切向应变，应变片分别布置在拱桥内壁的波峰、波谷和波侧位置，位置见图1。

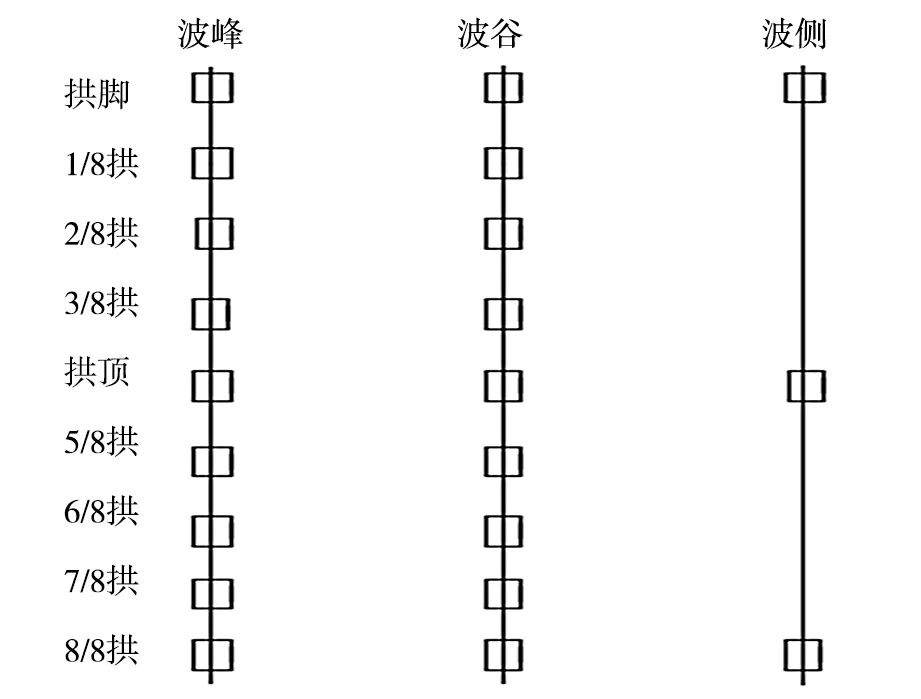
图1 拱桥内壁应变片位置布设

1.3 波纹钢板拱桥土压力测试方案

施工填土过程中对拱桥外壁土压力进行测试，测试不同拱顶填土高度时，拱桥拱周各位置的土压力变化情况。土压力盒和应变片的布设点相同，具体测点位置见图2。

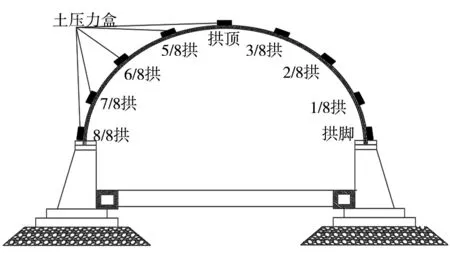
图2 土压力测试点位

1.4 波纹钢板拱桥应变与土压力测试工况

根据现场试验，分别对拱周填土测试其应变，对拱顶填土测试其应变和土压力，见表1、表2。拱周填土共6 m，拱顶填土共1.5 m，每填土一层，待机械压实结束后并远离钢波纹板拱桥，然后再采用静态应变测试仪与振弦频率测试仪对应变和土压力进行同步测试，并记录相关数据。

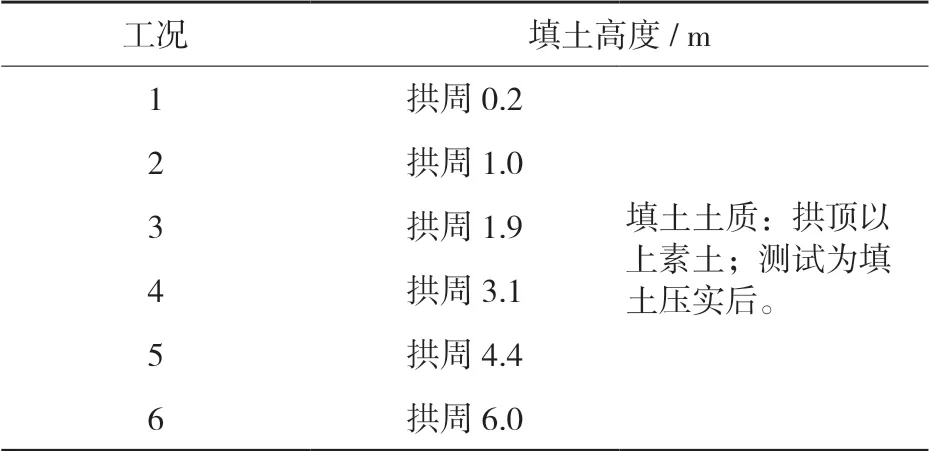
表1 拱周测试工况

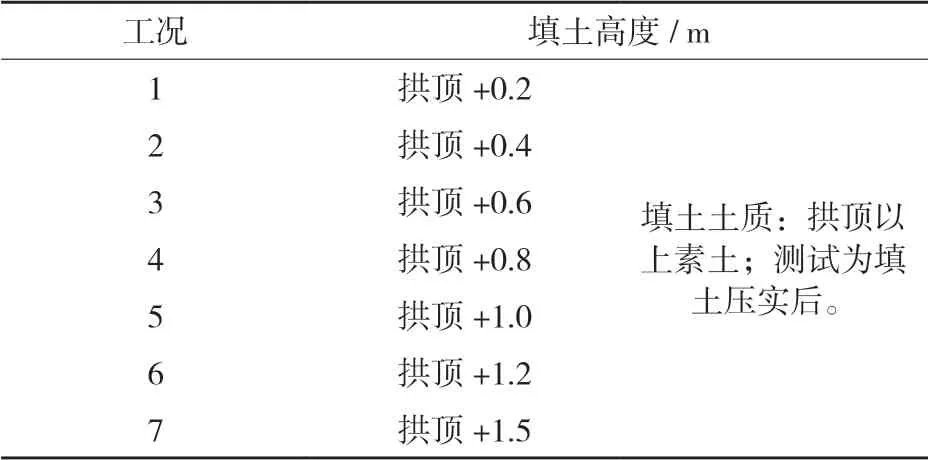
表2 拱顶测试工况

2 波纹钢板拱桥现场测试数据分析

2.1 拱周填土切向应变测试结果分析

2.1.1 波峰随拱周填土增加的切向应变

波峰切向应变规律见图3。

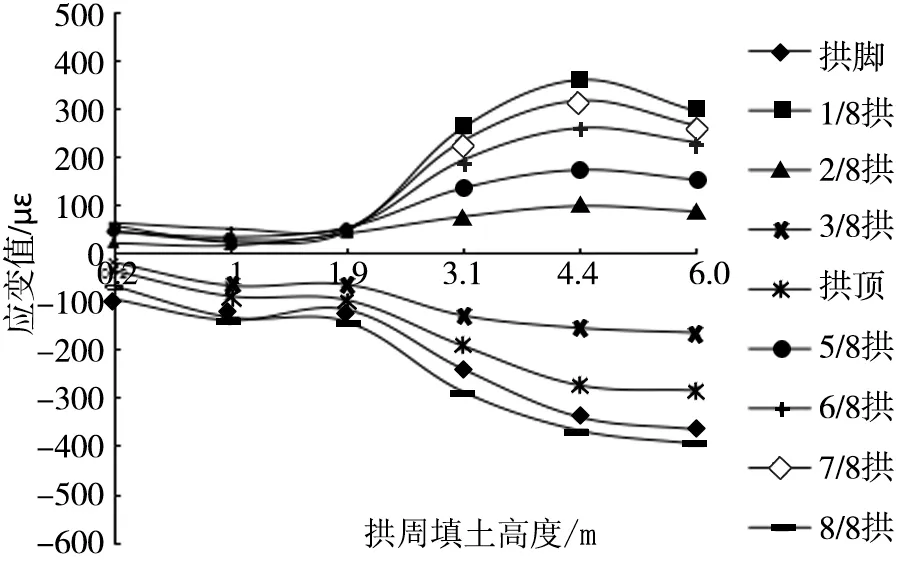
图3 波峰切向应变规律

从图3可以看出：（1）随着拱周填土高度的增加，整体拉、压应变趋势逐渐增加，且拉、压应变曲线规律具有一定的对称性。（2）拱周填土0.2 m时，应变值变化较小，填土增加至1.9 m处，拉应变出现应力集中，而压应变出现小幅减小。当拱周填土至3.1 m 时，拉、压应变值均出现了突变，并且迅速增加，增幅较大；填土至4.4 m，此时拉应变和压应变均达到最大值，之后填土高度至6.0 m，拉应变值出现小幅减小，而压应变逐渐趋于平稳。（3）拱周填土过程中，拉应变位于1/8拱、7/8拱、6/8拱、5/8拱和2/8拱位置，且最大拉应变出现在1/8拱位置；而3/8拱、拱顶、拱脚和8/8拱均为压应变，最大压应变在8/8拱位置。当填土增加至1.9 m时，发生了应力集中，施工中应注意重点观测并记录数据。

2.1.2 波谷随拱周填土增加的切向应变

波谷切向应变规律见图4，分析得出：（1）相比波峰，波谷应变值略小。拱周初始填土，拉压应变同时存在并呈交替变化趋势。拱周填土1 m，拱脚、3/8拱、拱顶、8/8拱均为拉应变，而压应变出现在1/8拱、2/8拱、5/8拱、6/8拱和7/8拱处；拱周填土 1.9 m，拉、压应变值均出现缓慢减小，当填土至3.1 m， 拉、压应变均在此时发生突变，应变值迅速增大，或许由于施工前期，机械压实度不足，后压实度增加引起；填土后期4.4～6.0 m，拉、压应变值出现缓慢增长并逐步趋向稳定。（2）填土至1.9 m，此时拉、压应变均出现应力集中，而填土过程最大压应变出现在1/8拱位置，最大拉应变在8/8拱位置。

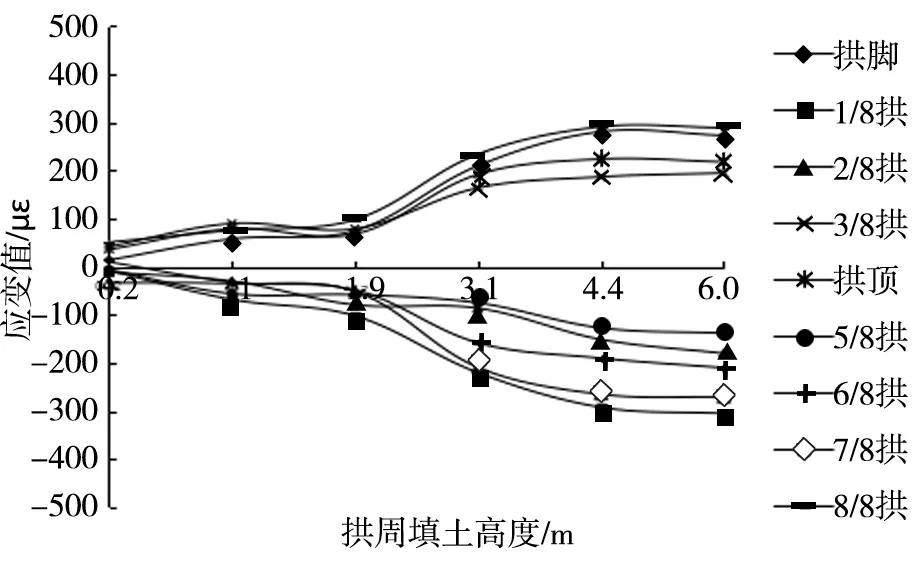
图4 波谷切向应变规律

2.1.3 波侧随拱周填土增加的切向应变

波侧切向应变规律见图5。

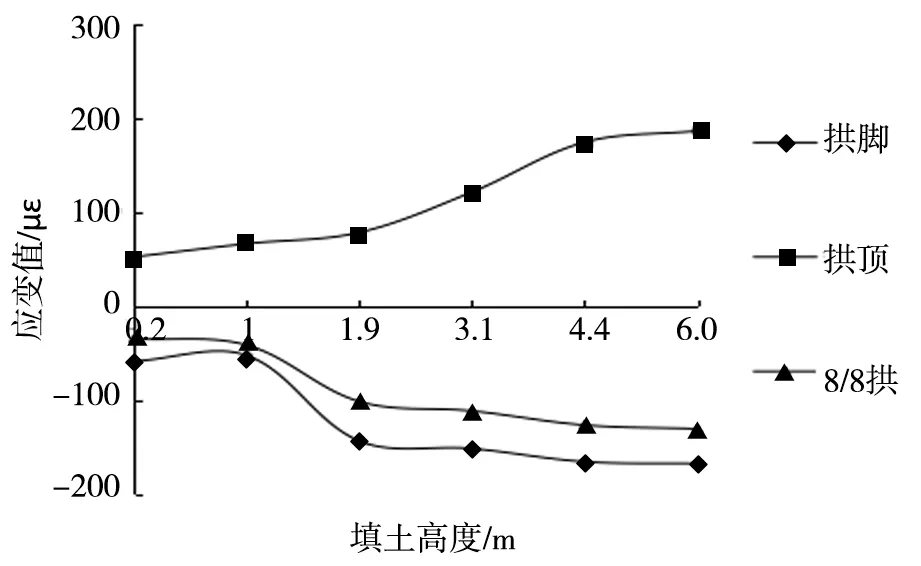
图5 波侧切向应变规律

从图5分析得出：（1）波侧随拱周填土增加应变逐渐增大，应变变化趋势相比波峰、波谷略小。整个填土过程中，拱顶为拉应变，而拱脚和8/8拱为压应变。（2）初始填土0.2～1.9 m，拱顶位置应变缓慢增加，而拱脚和8/8拱处压应变先缓慢增加后迅速增大；拱周填土1.9～4.4 m时，拱顶出现最大拉应变，而拱脚和8/8拱处压应变呈小幅增长规律；后期填土至6.0 m，拱脚、拱顶和8/8拱的拉、压应变值逐渐趋于平稳。

2.1.4 波峰、波谷和波侧随拱周填土增加的切向应变分析

通过图3～图5对比，分析得出：（1）波峰拱脚处压应变最大，且应变值相比波谷与波侧较大。波谷拉应变和压应变的变化规律与波峰正好形成互补。拱周填土1.9 m时，波谷各个位置出现拉、压应变交替的现象，而波峰出现应力集中。（2）拱周填土过程中，波峰应变值出现了突变，拱顶位置出现拉压应变交替的现象，并随填土高度增加逐渐趋向于稳定。波侧位置在整个填土过程，应变值先增大后趋于平稳，而拱脚和8/8拱位置为压应变，整趋势小幅增加。（3）总体来看，拱周不同填土高度下，波峰、波谷最大应变在1/8拱处，而波侧最大应变出现在拱脚位置。最大压应变为439με，最大拉应变为277με，整体上小于钢材的允许应变，波纹钢板拱桥安全稳定。

2.2 拱顶填土切向应变分析

2.2.1 波峰随拱顶填土增加的切向应变

波峰切向应变规律见图6。

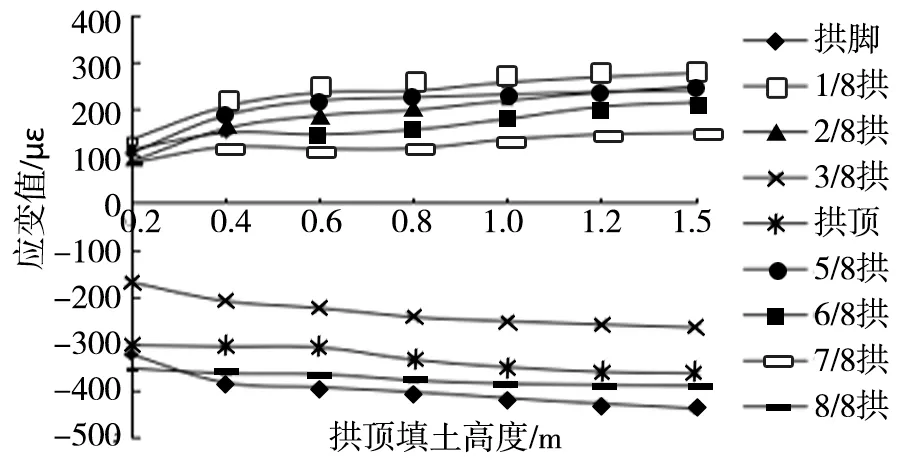
图6 波峰切向应变规律

由图6分析得出：（1）随着拱顶填土高度增加，波峰应变值缓慢增大，总体来看，拉、压应变的分布规律与拱周填土相似，拉应变主要分布在1/8拱、5/8拱、2/8拱、6/8拱和7/8拱，而压应变则分布于3/8拱、拱顶、8/8拱和拱脚位置。（2）起初填土0.2 m， 总体拉应变出现应力集中，而压应变值较为分散，填土到0.4 m,此时拉应变快速增加，压应变则缓慢增加，随拱顶填土不断增加，应变值增长率减小。（3）后期填土至1.5 m，此时拉应变各位置大小关系：1/8拱＞5/8拱＞2/8拱＞6/8拱＞8/8拱；压应变各位置大小关系：拱脚＞7/8拱＞拱顶＞3/8拱。其中压应变最大值位于拱脚，而拉应变最大值则位于1/8拱位置。

2.2.2 波谷随拱顶填土增加的切向应变

波谷切向应变规律见图7。

图7 波谷切向应变规律

由图7分析得出：（1）拱顶填土过程中，波谷应变变化规律与波峰恰好相反，拉应变位于3/8拱、拱顶、8/8拱和拱脚位置。而压应变出现在1/8拱、2/8拱、5/8拱、6/8拱和7/8拱位置。（2）随拱顶填土高度的增加，拉压应变都在逐渐增大，填土0.2～0.6 m，压应变增幅较大，而拉应变缓慢增加；当填土0.6～1 m时，拉压应变增幅较小，直至填土1.5 m，拉压应变几乎不再变化。（3）填土结束，最大压应变出现在2/8拱处，其余各位置大小关系：6/8拱＞1/8拱＞5/8拱＞7/8拱；最大拉应变位于拱顶处，大小关系：拱顶＞拱脚＞8/8拱＞3/8拱。

2.2.3 波侧随拱顶填土增加的切向应变

波侧切向应变规律见图8。

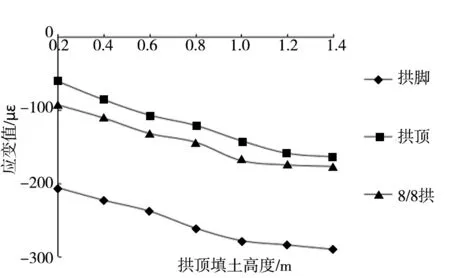
图8 波侧切向应变规律

由图8分析得出：（1）波侧随填土高度增加整体都为压应变，且随着填土高度的增加逐渐增大。（2）初期填土0.2～0.8 m，应变值增长较快，而当填土1.2～1.5 m时，压应变值出现缓慢增长，之后随填土高度的增加逐渐趋近于平稳。（3）波侧各测点压应变大小关系：拱脚＞8/8拱＞拱顶，且相比较于其它位置，增长斜率较大。

2.3 土压力测试结果分析

土压力变化规律见图9。

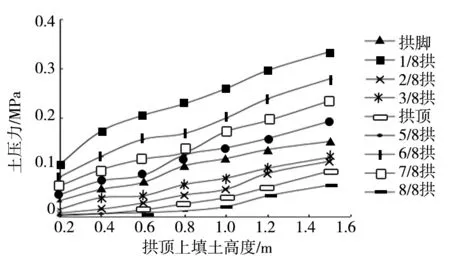
图9 土压力变化规律

由图9分析得出：（1）整体土压力变化规律为逐渐增加。初始填土拱顶0.2～0.4 m时，土压力逐渐增加。当填土拱顶0.6～0.8 m时，土压力值开始缓慢增加，拱周不同位置的土压力大小关系：1/8拱＞6/8拱＞7/8拱＞5/8拱＞拱脚＞2/8拱＞3/8拱＞跨中＞8/8拱。（2）当填土至拱顶0.8 m时，7/8拱和5/8拱土压力产生了突变，可能是由于施工过程中，小型夯机对钢波纹板拱桥产生扰动。拱顶填土至1.5m，土压力增幅较大。最大土压力在1/8拱处，最小土压力在8/8拱位置。

3 结语

对跨径10 m的波纹钢板拱桥进行现场试验，测试并分析拱桥不同位置的应变和土压力，可得结论：（1）拱周填土过程中，波峰与波谷变化规律相似，都在1.9 m填土处出现了应力集中，并在拱周填土3.1 m 时发生突变，整体趋势是缓慢增加→迅速增加→趋于平稳。（2）拱顶填土过程中，波峰、波谷和波侧应变值均随填土高度缓慢增加，波峰和波谷拉压应变相反，形成互补。（3）土压力在拱顶填土过程中，变化趋势为逐渐增大，初期增张较快，后期缓慢增加。（4）初始填土部分应变数值有波动情况，建议在施工过程中，适当减小拱周填土的厚度，提高压实度，有利于减缓钢波纹板拱桥的水平受力与竖向变形，从而使整个拱桥结构更加安全、可靠和稳定。