基于BAS-BP的钻井机械钻速预测模型
李 琪,屈峰涛,何璟彬,王六鹏,陈超凡
(1.西安石油大学 石油工程学院,陕西 西安 710065;2.川庆钻探工程有限公司 长庆钻井总公司,陕西 西安 710021;3.中国石化江苏石油勘探局 技术监督中心,江苏 扬州 225200)
引 言
提高钻井效率、降低钻井成本是钻井工程领域的重要研究内容之一。机械钻速是评价钻井效率的重要指标,而机械钻速的影响因素众多,主要可分为两类:一类是不可控因素,主要表征地层性质及岩石物性,如岩石类型、岩石可钻性、泥质含量、孔隙体积等;另一类是可控因素,主要有钻进过程的钻井液参数及作业参数,如钻井液密度、黏度、排量及钻压、转速、扭矩等[1-2]。精确建立机械钻速与影响因素之间的模型对预测机械钻速、优化工程参数至关重要。
国内外众多学者自上世纪五十年代以来建立了不同的机械钻速预测数学模型,按研究进展归为4个主要阶段:(1)现场数据统计回归预测模型。Maldia和Young F.S等[3-4]考虑岩石机械性质、钻头类型、钻压、转速、牙齿磨损、水利参数等因素影响,利用多元回归分析建立机械钻速方程。(2)考虑所钻地层性质和钻头结构的机械钻速预测模型。Maurer和Warren等[5-6]用可钻性强度S来反应岩石性质,并以实验为依据建立机械钻速预测方程,但由于岩石性质参数具有较大的离散性,限制了模型在复杂结构井的推广应用。(3)计算机仿真预测模型。在实验数据的基础上,应用计算机仿真来模拟钻头对岩石冲击、剪切破碎的过程,在冲击回旋机械钻速预测和钻进过程中的钻柱震荡等工作中应用效果良好[7-8]。(4)数据驱动的智能机械钻速预测模型。由于钻井环境复杂,钻井参数之间非线性关系明显,简单的数学模型很难实现精准的机械钻速预测,因此,该阶段研究以现场数据为基础,应用智能算法对数据隐性关系进行挖掘,构建智能模型,实现机械钻速预测[9]。
目前,数据驱动的SVR(Support Vactor Regression)、ELM(Extreme Learning Machine)、ANN(Approximate Nearest Neighbor)、GBDT(Gradient Boosting Decision Tree)等算法在机械钻速预测的智能模型建立中得到了广泛的应用[10-13]。但是,由于这些算法很容易陷入局部最优,且预测结果稳定性差,因此,需要开发基于混合算法的机械钻速预测模型。本文提出一种基于BAS(Beetle Antennae Search)优化的BP(Back Propagation)神经网络机械钻速预测模型,该模型以现场实测数据为基础,采用小波滤波方法对实测数据进行降噪处理;应用互信息进行关联分析,确定模型输入参数。
1 BAS-BP模型
1.1 BP神经网络
图1为BP神经网络的拓扑结构。BP神经网络一般由1个输入层、1个或多个隐含层和1个输出层组成。
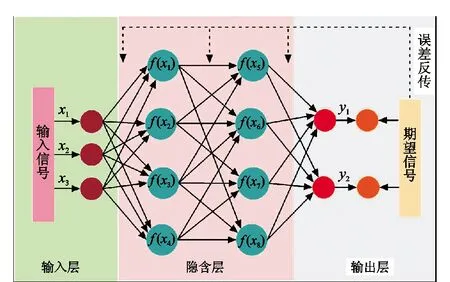
图1 BP神经网络的拓扑结构
BP神经网络的训练过程主要包括信息的正向传递和误差的反向传播,其学习规则是使用最速下降法不断调整网络的权值和阈值使得网络误差最小,最终达到满意的预测结果[14]。
1.2 BAS算法
天牛须搜索算法是基于天牛觅食原理而开发的一种适用于多目标函数优化的新算法[15]。天牛在觅食过程中,根据左、右两须接收食物气味信号的强弱差异来判断食物位置,逐渐优化自身飞行方向,直至找到食物的位置[15-16]。
BAS算法具体步骤如下:
①创建天牛须朝向的随机向量并作归一化处理
(1)
式中:rands()为随机函数;n为空间维度。
②创建天牛左、右两须的空间坐标
(2)
式中:xlt、xrt分别为天牛左、右两须在第t次迭代时的位置坐标;xt为在第t次迭代时的天牛质心位置;d为两须之间的距离。其中,xt,xlt,xrt均为n维向量。
③根据适应度函数f(x)判断左、右两须的气味信号强度,即f(xlt)和f(xrt)的值:
(3)
式中:m为训练集样本数;ysim(i)为第i个样本的模型输出值;yi为第i个样本的真实值。
④迭代更新天牛质心位置
xt+1=xt-δt·b·sign(f(xrt)-f(xlt))。
(4)
式中:δt为第t次迭代的步长因子;sign()为符号函数。
1.3 BAS-BP模型
BP神经网络在训练过程中完全依赖误差函数实现对随机生成的初始权值和阈值的调整,权值、阈值选择不当将对结果产生极大影响[17]。很多研究表明,通过优化算法对初始权值、阈值进行优化,将极大提升网络性能,避免随机初始化造成网络陷入局部最优。本文采用BAS优化算法,将BP神经网络的权值、阈值集合设为搜索空间,寻找最优的初始权值和阈值,并将其应用于构建好的BP神经网络中,完成模型训练。
基于BAS优化的BP神经网络预测模型流程如图2所示。具体步骤如下:

图2 基于BAS优化的BP神经网络预测模型流程图
Step1 创建BP神经网络,并初始化网络参数。
Step2 创建天牛须朝向随机向量,确定搜索空间维度,设搜索空间维度为k,
k=I·H+O·H+H+O。
(5)
式中:I为输入层神经元个数;H为隐含层神经元个数;O为输出层神经元个数。
Step3 设置步长因子j,用来控制天牛的区域搜索能力。
Step4 确定适应度函数。
Step5 天牛质心位置初始化,初始参数取[-1,1]的随机数作为天牛须算法的初始解,并将其保存于bestX中。
x=rands(k,1)。
(6)
式中:x为天牛的质心位置,k为一维列向量。
Step6 计算初始天牛质心位置的适应度函数值,并将其保存于bestY中。
Step7 根据式(4)更新天牛位置,进行迭代实验。
Step8 判断迭代是否结束。根据适应度函数值是否达到预先设定的精度(goal1=0.001)或迭代次数是否达到最大次数(n1=100)来确定迭代是否停止,迭代结束则输出最优权值和阈值。
Step9 新建网络。根据BAS优化结果,初始BP神经网络的权值和阈值,设置网络训练次数(n2=1 000),训练目标(goal2=0.000 001)和学习效率(rate=0.01)。
Step10 计算各层输出及误差,修正权值、阈值,重复迭代训练。
Step11 判断算法是否结束。根据适应度函数值是否达到预先设定的精度(goal2=0.000 001)或者迭代次数是否达到最大次数(n2=1 000)来确定迭代是否停止。
2 基于BP-BAS的机械钻速预测建模
2.1 机械钻速影响因素
影响钻头在破岩过程中机械钻速的可控因素主要分为机械参数、钻井液参数及水力参数。机械参数主要有钻压、转速、钻头类型、立管压力等,通过影响钻头对岩石的研磨、剪切过程来影响机械钻速。钻井液参数有钻井液体系、密度、初切力、流变参数等,钻井液性能和流变参数通过影响循环压力损耗和井底净化等来间接影响机械钻速。水力参数有水射流速度、射流功率、钻头压降等,通过保持井底净化从而影响机械钻速。
Bourgoyne[4]和Young综合考虑地层参数、工程参数及钻井液流变参数建立钻速方程。在此基础上本文对采集的钻井井史数据、综合录井数据进行筛选,以机械钻速、转速、钻压、排量、立管压力、井深、井径以及钻井液稠度系数等8种参数作为影响因素,建立机械钻速预测模型。
2.2 模型输入参数预处理
2.2.1 小波滤波处理
由于复杂钻进环境存在各种干扰,测量仪器接收的实测值与实际值之间存在一定误差,应用小波变换进行处理,小波变换继承了傅里叶变换的局部化思想,同时又克服了窗口大小不随频率变换的缺点,能够提供一个随信号改变的“时间-频率”窗口[18]。
将分析信号X(t)作小波变换,即
(7)
式中:a为尺度因子,且a>0,实现对基本小波φ(t)进行伸缩变换;τ为平移因子,实现对基本小波在时间轴上的平移变换。
应用软阈值进行降噪处理,提取第4层分解结果作为降噪后的输出结果。如图3所示,原始数据曲线包含许多尖峰和突变,应用强制降噪处理后的曲线较为光滑,有效地去除了原始信号中的尖峰和突变,同时降噪后曲线与原始曲线走势一致,保持原始数据的变化特性。

图3 小波降噪处理效果对比
2.2.2 数据归一化
为了消除输入、输出参数在数量级上的差异,提高模型数据处理的泛化能力,数据降噪后,对其进行归一化处理。采用归一化公式
(8)
将参数值归至[-1,1]区间。式中:xnorm为归一后的数值;x为归一前的数值;xmax、xmin分别为数据归一前的最大值、最小值;ymax、ymin分别为数据归一后的最大值、最小值。
2.3 互信息关联分析
分析钻井参数间的相关性,可以筛选输入参数,降低所建钻井机械钻速模型冗余。图4左下三角位置为各变量之间的散点图;图4对角线位置为核密度函数图。从图4可以看出,钻井参数间主要表现为非线性相关,常用的Pearson系数法、回归分析法,能有效地量化变量间线性关系,无法表征非线性相关变量间的相关性[19]。
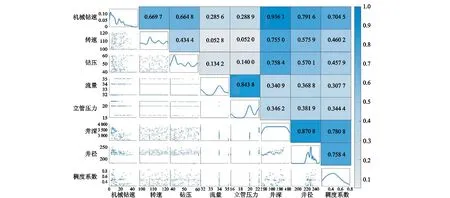
图4 钻井参数相关性分析
为了方便表征非线性相关变量之间的关系数值,实现量化统计,引入互信息关联分析[19]。互信息是用来衡量变量间非线性关系的常用方法,当(X,Y)~p(x,y),则变量X、Y之间的互信息定义为
MI(X;Y)=H(X)+H(Y)-H(X,Y)。
(9)
式中:H(X,Y)为变量X、Y的联合熵;H(X)、H(Y)分别为变量X、Y的无条件熵。
为了便于评价,将互信息作归一化处理,则
(10)
NMI(X;Y)的值反应变量X、Y之间的相关性大小。
图4右上角为各钻井参数间的互信息热力图。图中机械钻速与其他各钻井参数的相关性大于1/m(m为输入模型的参数个数,此处m=8),可见机械钻速与转速、钻压、井深、井径、钻井液稠度系数等钻井参数相关性强,与排量和立管压力的互信息值相关性较低,因此,筛选转速、钻压、井深、井径、钻井液稠度系数等5个参数作为机械钻速预测模型的输入变量。
2.4 BAS-BP机械钻速预测建模
BAS-BP机械钻速预测模型建模流程如图5所示。BAS-BP机械钻速预测建模整体主要分为5个部分:第1部分为实测数据清洗,主要完成数据采集与整理,以及对整理后的数据进行滤波降噪;第2部分为相关性分析,主要完成为互信息分析实现对模型输入参数的筛选;第3部分为BAS优选初始权值和阈值,确定BP神经网络架构,应用BAS优化算法对BP神经网络初始权值和阈值进行优化;第4部分为BP神经网络模型训练,将相关性分析筛选的参数作为模型输入,以机械钻速作为模型输出进行模型训练;第5部分为误差分析和模型评价,若模型预测精度达到设计要求则输出模型,反之则根据BP神经网络内置罚函数对权值和阈值进行优化,重复训练,直至精度达到设计要求则输出模型。
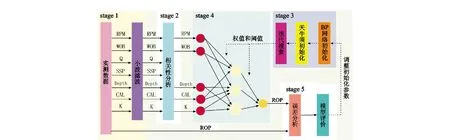
图5 机械钻速预测模型建模流程
3 实验验证与结果分析
本次实验数据来自现场某区块定向井作业数据,该井完井时间为2020年4月,井型为采油井,设计井深3 800 m,实钻井深3 720 m,造斜点位于井深1 900 m处,完井方式为射孔完井,钻井周期23 d,平均机械钻速12.52 m/h。
为了验证BAS-BP神经网络模型较其他优化后的智能模型是否具有优越性,将其与标准BP神经网络模型、PSO-BP神经网络模型、GA-BP神经网络模型进行对比分析,结果见表1。
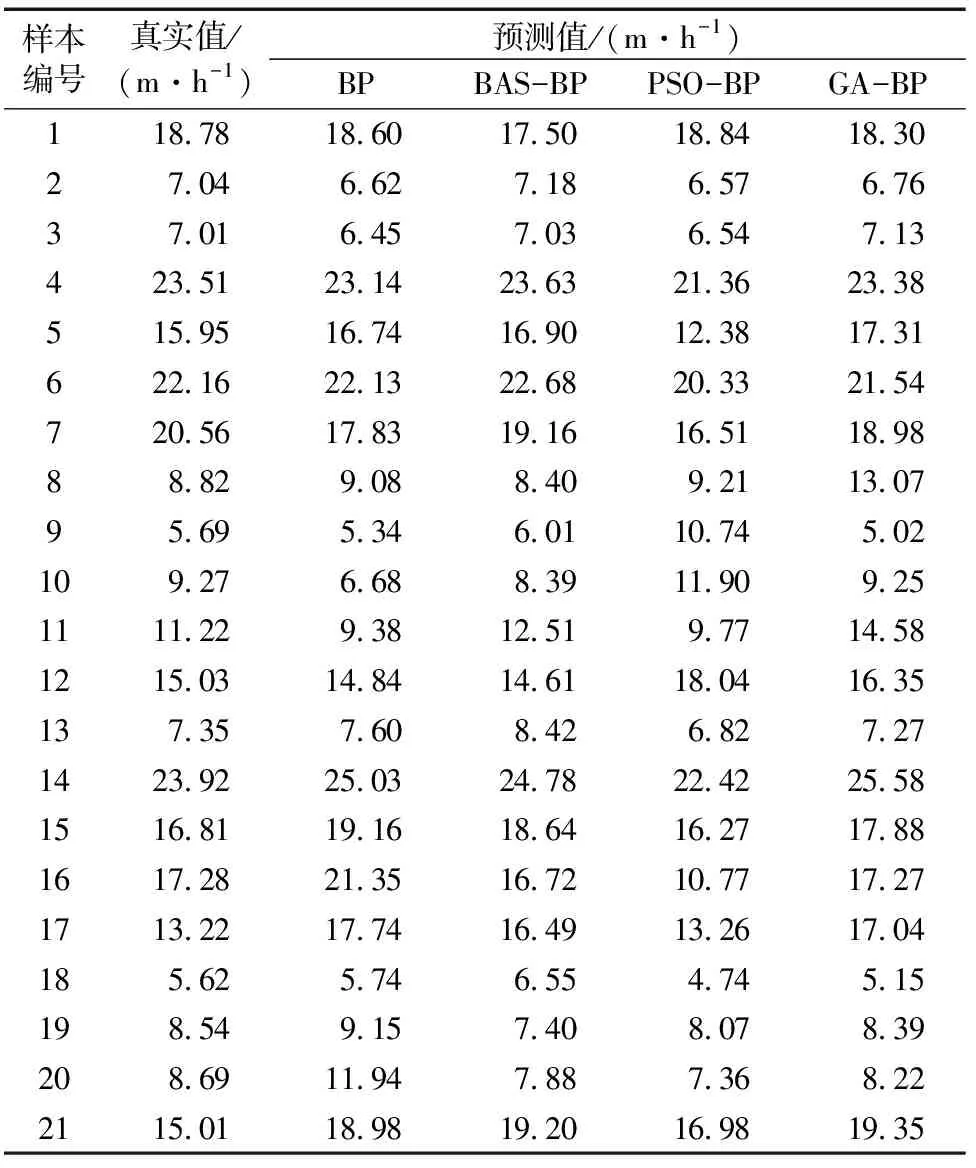
表1 BAS-BP模型与其他BP模型测试集预测结果
图6为BAS-BP模型与其他BP模型预测结果对比。图6中各钻速模型预测值与实际测量值折线走势一致,可见各钻速模型均可实现机械钻速预测,但各钻速模型预测值与实际测量值之间存在偏差。
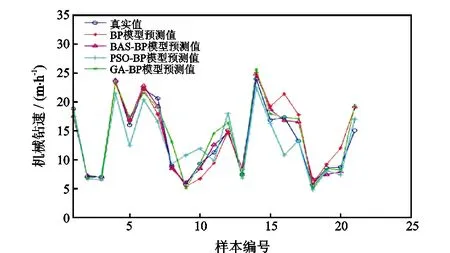
图6 BAS-BP模型与其他BP模型预测结果对比
选取均方根(RMSE)、平均绝对百分比误差(MAPE)、决定系数(R2)作为评价指标对模型性能进行评价[21]。各评价指标计算结果见表2。
图7为BAS-BP模型与其他BP模型预测误差对比。由图7可知,BAS-BP模型与GA-BP模型的误差波动范围较小。但是,根据表2显示,本文提出的BAS-BP模型较GA-BP模型的均方根误差和平均绝对百分比误差分别降低22.92%和14.71%,并且BAS-BP模型的R2值最大。R2是最常用于评价预测模型优劣程度的指标,R2越大(接近于1),表明所建立的预测模型越优,即模型预测值越接近实际测量值。由此可见,本文提出的BAS-BP机械钻速预测模型相比其他3种BP神经网络模型,具有最好的预测精度。
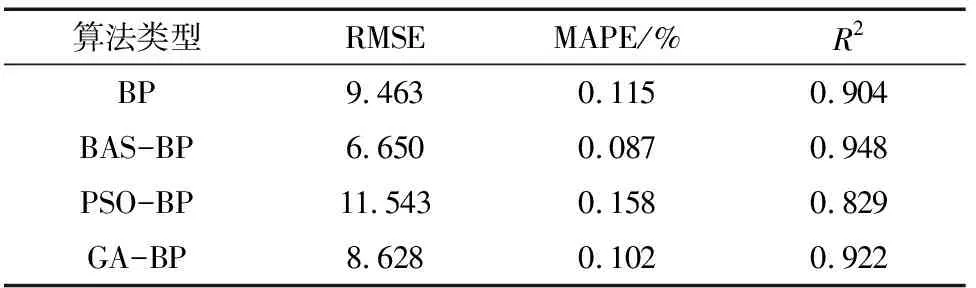
表2 BAS-BP模型与其他BP模型评价指标对比

图7 BAS-BP模型与其他BP模型预测误差对比
4 结 论
(1)对于机械钻速预测这类变量多、非线性强的数据预测问题,应用小波滤波方法和互信息关联分析,能够有效地降低噪声干扰和模型冗余,简化运算过程。
(2)应用BAS-BP神经网络预测模型,克服了标准BP神经网络稳定性差、收敛速度慢、易陷入局部最优等缺点,提高了网络的性能及预测结果的精度。
(3)研究证明了数据驱动模型在钻井机械钻速预测应用中的可行性和有效性,但也有不足之处,由于完整样本较少,研究结果仅停留在计算机仿真模拟,为了加强预测模型的泛化能力和通用性,需要进一步收集充分的样本数据。

