基于K-means对马赛克瓷砖选色问题的研究

吴 妍 吴靖轩 晏 丽 向彩容

（江汉大学人工智能学院,湖北 武汉 430056）

马赛克瓷砖是一种尺寸很小的正方形瓷砖，可用于非平整面铺设，通过拼接可以组合成给定的文字或图案。由于成本、技术、需求的限制，厂家一般只生产有限种颜色的瓷砖。为了减少人工选色的工作量，需要构建一个智能配色系统，能确定原始颜色与瓷砖颜色的对应关系，从而能够根据图片颜色自动找出颜色最接近的瓷砖。

1 问题分析

本文以两幅样本图片为例（图片1和图片2）和假定某厂当前生产的瓷砖颜色开展对上述问题的研究，该问题可分为三个层面。

问题一：给定厂家目前生产m种颜色的瓷砖（取m=22），找出与给定图片颜色最接近的瓷砖颜色。该问题是找到图片颜色与指定颜色集中颜色的模型关系，并说明模型的好坏。

问题二：在只考虑图像拼接表现力的情况下，若厂家想增加不同颜色的瓷砖，确定应优先增加哪种颜色的瓷砖。该问题是基于问题一的模型，以表现力最大为目标，针对具体图片，在瓷砖颜色库的种类及数目固定下，增加聚类中心点的问题。

问题三：假定每种颜色的开发成本和技术难度相同，综合考虑成本和表现效果，确定新增几种颜色及哪几种颜色。该问题是从实际问题出发，不考虑生产技术的难度，假定不同颜色瓷砖成本相同，并在问题二的基础上，综合考虑生产成本和表现力效果，寻找平衡点。

2 模型假设

（1）假设问题中的瓷砖实际颜色与其RGB值表示的颜色完全对应。

（2）假设问题中的瓷砖大小相同，边缘完好，能够完美拼接。

（3）假设每种颜色的开发成本和技术难度是相同的。

3 符号约定

（3）△eij：表示客户所给图像中的第j种颜色和该厂生产的第i种瓷砖颜色的色差。

（4）△Eij：表示客户所给图像中的第j种颜色与其对应的相近色i的色差。

（5）dij：表示第i种颜色与第j种颜色之间的距离。

4 模型建立与求解

4.1 问题一模型：K-Means聚类算法[1]

4.1.1 模型建立

（1）数据处理

图片1包含216种颜色，图片2包含200种颜色，其中图片1、2的RGB值示例如表1。

表1 图片的数据表现形式

①特征转换[2-3]

RGB色彩具有R（Red）、G（Green）、B（Blue）三通道，各有256级亮度，取值从0、1、2……直到255。其三通道有较强的相关性，主要表现为若某一通道增大，则像素的其他通道值也随之增大。

常见的颜色特征空间还有HSV空间、Lab空间等。HSV特征是一种描述颜色的方式，H（Hue）是色调，用角度量来表示，范围是0～360；S（Saturation）是饱和度，表示成所选颜色的纯度和该颜色最大的纯度之间的比率，范围是0～1；V（Value）是亮度，表示色彩的明暗程度，范围是0～1。相比RGB，HSV特征更容易跟踪某种确定的颜色，因此选择将RGB特征转换为HSV特征。RGB特征到HSV特征的变换如下式：

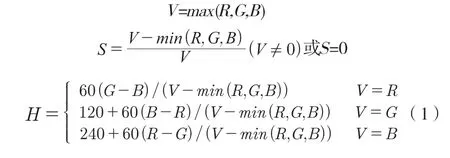
If H ＜0，then H=H ＋360；0 ≤V ≤1，0 ≤S ≤1，0≤H≤360。

②归一化

本文挑选欧氏度量作为聚类度量L2，先对特征进行归一化。归一化公式如下：

其中x、y分别为转换前、后的值，MaxValue、MinValue分别为样本的最大值和最小值。

（2）模型建立

K-means聚类是选择k个初始聚类中心，给定度量，根据待分样本到初始聚类中心的距离将样本数据分到最近的聚类中心所在的类，再重新计算各个聚类的中心，重复操作至满足条件。具体步骤如下：

第一步，将图片中的RGB值转换成HSV值；

第二步，将第一步的结果进行归一化；

第三步，采用度量L2，计算图片中第j片与现有瓷砖颜色i的距离，对于图片中的第j片，挑选距离dij中最小所对应的第i块瓷砖作为相似色，并记录其编号。

4.1.2 模型结果及分析[4-5]

图片1、图片2基于瓷砖颜色库挑选出了最相近的瓷砖的颜色编号。表2是以图片1中3个颜色为例，列举出的对应相似瓷砖的颜色。

表2 图片1中3个颜色和其对应相似瓷砖颜色

挑选国际标准CIE中的色差作为描述表现力效果的指标，色差值越小表明两张图像越相似。采用颜色的HSV值进行计算。第j种颜色和该厂生产的第i种瓷砖颜色的色差计算公式如下：

计算所得图片1、图片2与基于图片挑选的瓷砖颜色图片间的色差分别为2.416、1.717，根据国际CIE的标准（如表3），所选瓷砖颜色和图片1中颜色有一定的差距，而所选瓷砖颜色和图片2中颜色的差距为中等，在特定应用中可以接受。

表3 国际CIE色差标准

4.2 问题二模型：K-means聚类算法、基于目标函数的搜索法

4.2.1 模型建立

（1）数据处理

瓷砖颜色的选择依赖于给定图像的颜色分布，现以图片1为例来进行颜色的挑选，先将图像1中216种颜色的RGB值转化为HSV值。

（2）模型建立

首先采用K-Means算法，再基于目标函数的搜索法给定目标函数，在给定范围内搜索出最优解。具体步骤如下：

第一步，以图片1中的216种颜色和22种瓷砖颜色为对象，采用K-means算法搜索类中心集，作为待选集K。在上述待选集K里去除已有的22种瓷砖颜色，将剩余类中心作为待选集；

第二步，将色差作为描述表现力效果的量，对于固定的k（k=1，2，…，10），在待选集K中挑k种颜色，并用问题一的模型对图片1进行铺片，计算色差均值；

4.2.2 模型结果及分析

同时增加k种颜色所对应的色差和颜色的RGB值如表4，可以看出随着添加颜色个数的增加，色差逐渐减小。从模型运行速度来说，当同时添加10种颜色时，整个程序运行时间为10 min左右，体现出该模型具有较高的准确性和较好的高效性。

表4 同时增加k种颜色所对应的色差和颜色的RGB值

4.3 问题三模型：优化模型

4.3.1 模型建立

假设不同颜色的瓷砖生产成本相同，以色差描述图像表现力为目标函数，建立关于添加颜色的个数与色差的模型，同时考虑总成本与表现力效果的关系，寻找函数图像的平衡点。

4.3.2 模型结果及分析

从图1和图2可以看出，当同时增加8种颜色后，色差值趋于稳定，其一阶差分值趋于0，即该点为最优解。

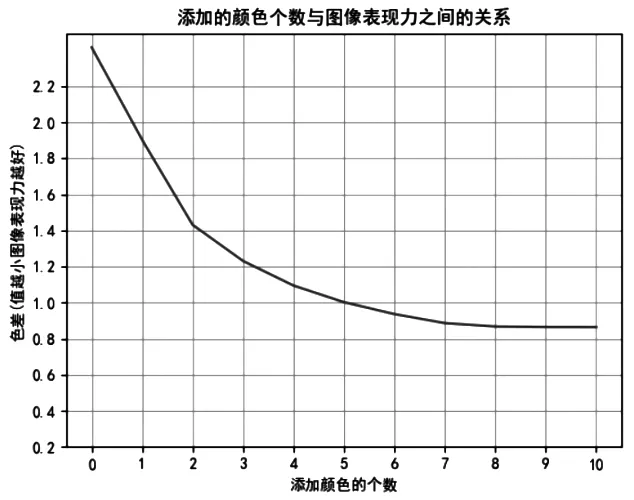
图1 添加颜色的个数与图像表现力的函数关系图

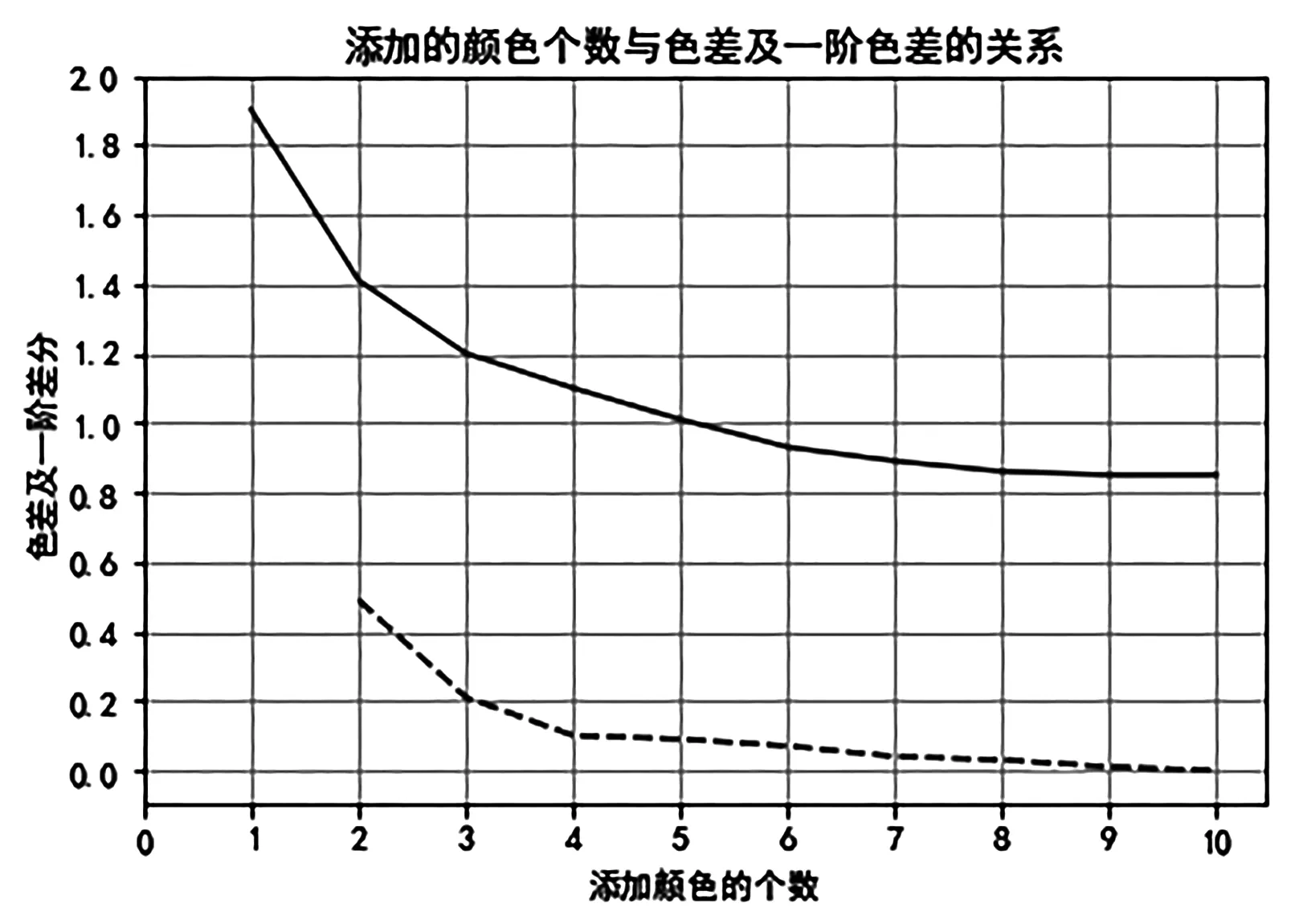
图2 添加颜色的个数与色差和色差一阶差分的关系图

5 模型改进与优化

为了检验模型一，将图片1中的216种颜色和图片2中的200种颜色组合成新的图片，并从中随机选取200种颜色带入模型，算得色差为3.219。根据国际CIE的标准，所选颜色和图像3中颜色存在一定差距，在特定应用中可以接受。对于模型二，模型分别计算了同时增加k种颜色时的色差均值，都处于国际CIE色差标准中微小到中等的范围，说明模型泛化能力不错。

通过模型检验可以看出，该模型具有较好的准确性以及较高的效率。但模型是基于提供的一张或多张图片来决定所增补瓷砖颜色的方案，为了增强其应用性，可收集大量各种类型的图片，利用图片对该模型进行训练，从而找到公共的增补方案，即为马赛克瓷砖选色问题的最优解。