把握思维起点 实现有效学习
江苏省苏州市吴江区八坼小学 褚琴华
数学是思维的体操。教学中,要把握学生数学学习思维的起点,暴露出学生思维的真实状态,通过高质量的思维活动,引领有效的数学学习,让学生的学习过程更真实、丰富,学习体验更深刻。
一、把握学习的起点,暴露“真”思维
教学要展现学生进入学习的基础性状态,激发学生展开数学思维的内在动力,激发学生已有的数学知识经验和心理能力,否则就不能吸引学生真正参与。教学时要充分了解学生的真实需求和学习起点,暴露学生的思维状况,分析其内在机制,才能更有效地启发学生数学思考,将教学活动引向更深的层次,促进学生思维水平的逐步提升。
例如:教学“三角形的面积计算”,这一课建立在刚刚学习了平行四边形面积计算的思维基础之上,大部分教师都会直接提供一个一般三角形进行教学,虽学生有一定的学习起点,但运用“剪拼”的方法将三角形转化成平行四边形,或者想到要用两个完全一样的三角形来拼,其实对于学生而言是有难度的。教学时,不妨设计如下几个步骤,让学生真正地暴露其思维,逐步完成探索过程。“①等腰三角形可以转化为什么图形?怎样转化?②直角三角形可以转化为什么图形?怎样转化的?③一般三角形如何转化呢?”这样学生能顺利从“剪拼法”过渡到“组拼法”来探索三角形的面积计算,而且更重要的是能让不同层次的学生都真正参与到课堂中去。
又如:一位教师教学“用画线段图的策略解决和差问题”时,大胆尝试了“背道而驰”的复习导入,却收获了意想不到的效果。由“复习题:灵灵和春春共有72张画片,已知灵灵和春春画片的张数相等。他们两人各有多少张画片?”引入“例题:灵灵和春春共有72张画片,已知春春比灵灵多12张画片。两人各有多少张画片?”学生尝试列式,大部分列式为:春72÷2=36(张);灵36+12=48(张)。老师就利用这个错误契机,让学生讨论“这个答案合理吗?为什么?”学生思考片刻后便找到多方面的理由来说明这样解答是不合理的。此时教师结合画线段图分析,学生很顺利地得出方法一:72-12=60(张),灵灵有60÷2=30(张),春春有30+1=42(张)。解答后,老师提出“总数72张,就一定不能先平均分除以2吗?”学生经过点拨,便得到了第二种解法:要使两人画片张数相等,春春要把多出来的一半6张给灵灵。72÷2=36(张),原来春春:36+6=42(张); 灵灵:36-6=30(张)。最后,让学生观察线段图,比较几种不同的方法,说说有什么共同的特点。
教学中,教师敢于直面问题,暴露学生的真实思维。例子中复习题的出示,看似对新知的学习产生了“先平均分除以2”的“负面影响”。实质不然,这正是学生认知的自然展开,后续的教学中,教师能够很好地立足于学生的这一思维起点展开教学,让学生在复习题与例题的对比中深刻认识到——“平均分”必须两种数量要相等,这样一个核心的思维转折点让学生明白“可以把多的减掉,或者少的补上,甚至还可以把多出来的一半分给少的”,解决方法多样,但不管用哪种方法最终都要达到“把两种不相等的数量转变为相等后,才能平均分”这样的思维高度。只有将思维的难点真正融入到学生真实思维的分析之中,才能让学生在复杂的情境中进行辨别、分析、判断、推理,提高了教学的有效性,发展了学生的思辨能力。
二、关注学习的宽度,引发“真”思考
针对对课堂中的不确定性、课堂生成性的担忧,唯恐失去对课堂教学进程的主动把控或是担忧不能完成预定的教学任务,多数教师的课堂会走向“小步走、步步为营”的课堂结构。这样的教学形式很难激发学生内在的学习需求,不能给学生带来富含挑战性的思维活动,自然也不能形成真正意义上的师生互动,生成性资源也就较为匮乏。教学需要勇敢做出跨步,在开放性的思维教学中,尝试让学生用具体的实例来实现对知识的理解和建构。关注学生的学习宽度,对学习过程进行多样化的设计,使学生在课堂中能大胆地去探索、发现、理解数学奥秘,引发学生真正的思考。
例如:在“认识百分数”一课中,教材呈现了“三场比赛的投中次数和投篮次数(第一场投中16投篮25;第二场投中13投篮20 ;第三场投中18投篮30),让学生比较哪一场的投篮成绩更好”的问题情境,大部分学生认为可以比“未投中的次数”,第二场未中次数最少,所以成绩最好。此时,班里出现反对的声音,认为应该比“投中比率”,即“投中的次数占投篮总次的几分之几”。但巧合的是,比“投中比率”还是第二场成绩最好。这时出现了学习上的矛盾点,应该如何处理?显然,比“未投中次数”是不合理的,那该怎样给学生解释这种不合理性,又该怎样证实比“投中的比率”这种方法更合理呢?接下来,我引导学生思考:“比未投中次数,在这里的确也得到了正确的结果,那么这种方法是否适用于所有的情况呢?”学生陷入了沉思,片刻之后,有学生表明自己的想法:“我认为如果换了数据,这种方法就不可行了,比如第一场投篮10次投中9次,第二场投篮100次投中98次,虽然第一场只有1次未中,第二场却有2次未中,但很显然应该是第二场成绩更好,因为第一场是10次里面1次未中,而第二场是50次里面2次未中,第二场未中的几率更小一些,所以第二场成绩好,说明比‘未投中次数’是不合理的。”这里,马上追问:“比‘未投中的几率’可以吗? “比‘未投中的几率’和比什么是类似呢?”“看来比‘未投中的次数’有时是不科学的,比‘投中的比率’或‘未投中的几率’才是合理的。”
三、拓展学习的深度,引领“真”学习
数学是思维的科学,数学教学的根本任务是让学生学会思考,并且是有深度的思考。很多的数学课堂中,教师的问题是一个接着一个,学生的思考也是一次接着一次,可在众多的思考当中,有思维含量的思考活动却很少。课堂教学时,教师需要给予学生足够的时间和空间,找准机会,让学生体验到高品质的思维活动,引导他们进行多角度多层次的个性化思维,从而扩大学习的深度,引领“刻骨铭心”的真学习。
例如在“平面图形的复习”教学中,我设计了以下三个教学活动:
(1)边理边围三角形。提示:准备四种规格(2cm、3cm、4cm、5cm)的小棒,且每种根数足够多。任选三根围三角形,先想需要选择几种小棒,这样围成的三角形的名称是什么;再与同桌交流它的特征,如果有疑问或困难,动手围一围,合作完成研究单。
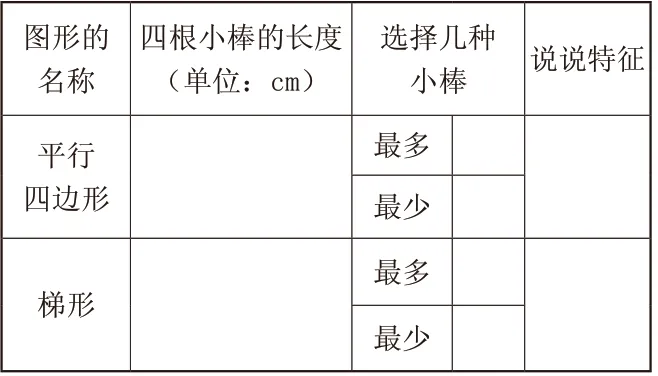
图形的名称四根小棒的长度(单位:cm)选择几种小棒 说说特征平行四边形最多最少梯形最多最少
(2)边理边围平行四边形与梯形。提示:任选四根围平行四边形,在表格中记录小棒的长度,小组探讨:围成平行四边形最多选几种小棒,最少呢?遇到困难同样动手围一围。梯形也是同样方法进行整理,再合作完成如下研究单。
(3)比一比,在下面两组图形中你发现了什么?
①将长方形拉成了平行四边形:

②平行线间的长方形和平行四边形:
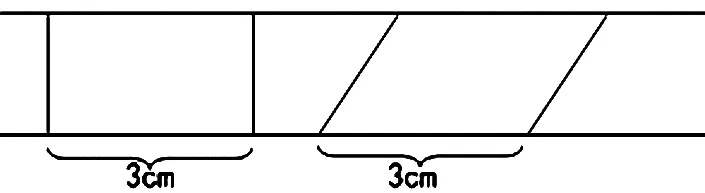
教学中,精心设计了两次“围”和一次“比一比”的活动,在研究单的指引下,操作前先思考:围什么?怎样围?如果基于感官体验的学生,在脑海中能建构正确的直观图形的表象,可以在研究单中设计整理环节,学生自然而然就会将零散的每个图形知识梳理成知识结构体系。在整理遇到困难时去围一围,学生边回忆边整理,知识得以巩固,且在操作中辨析释疑,在操作后整合总结,沟通各个图形之间的联系,帮助学生构建合理的认知结构与知识网络。以连贯而高质量的思维活动引领学生去操作、辩论、验证,此时的学习过程也就变成围绕一个“核心问题”研究的过程,提高了思考的质量,拓展了学生思维的空间,培养学生思维的全面性。
总之,数学是一门具有丰富思维活动的科学。在教学中,我们要注重知识之间转换过程,寻找相关知识间的内在联系,拓展学习思维的落脚点,促进学生思维水平的逐渐提升,从而提高学生的数学能力,实现有效学习。

