地基GNSS-IR风速反演原理及方法初探

王笑蕾，何秀凤，陈 殊，张 勤，宋敏峰

1. 河海大学地球科学与工程学院，江苏 南京 211100； 2. 长安大学地质工程与测绘学院，陕西 西安 710054

随着全球导航卫星系统(Global Navigation Satellite Systems,GNSS)的不断发展，过去被认为是误差源的多路径效应，已经被证实可以用来监测反射面物理参数，并逐步发展为GNSS反射遥感(GNSS reflectometry,GNSS-R)技术。其中的地基分支被称作GNSS干涉遥感(GNSS-interferometry reflectometry,GNSS-IR)技术[1]。目前，GNSS-IR已经被证实可以对水位[2-4]、雪深[5-9]、植被指数[10]、土壤湿度[11-13]、地表冻融[14]等相关参数进行反演。为了扩展地基GNSS技术的监测对象和应用范围，本文提出了一种基于GNSS-IR的风速反演方法。

利用反射信号进行风速探测在星载GNSS-R中已经实现，并有相关测风卫星播发[15]。星载GNSS-R测风的思路为：不同的风速会导致不同的海面粗糙度，进而导致反射信号的不同。依据反射信号的特征，就可以反推风速。这样的思路对于地基GNSS-IR同样适用，即利用反射信号特征推演粗糙度及风场信息。目前，关于GNSS-IR海面粗糙度反演及海面风场反演的研究较少。文献[16]利用信噪比(signal-to-noise ratio,SNR)的衰减参数对海面有效波高进行反演。文献[17]利用信噪比的多径截止高度角参数，提出了一种GNSS-IR风向反演方法。然而，该方法对于站点要求较高，需要站点四面环海，接收到全方位角海域反射信号，才能够确定风向。相关研究表明：SNR衰减因子及多径截止高度角可以反映海面粗糙度及风场信息，而且多径截止高度角参数更为准确[16-17]。

因此，本文将利用多径截止高度角参数进行风速反演。而获取该参数的方法目前主要基于曲线拟合方法和经验阈值，两种方法对于SNR的质量要求较高[17]。由于小波分析可以探测SNR序列的细节信息，已经有相关研究将小波分析应用到SNR的细节信息探测中。文献[18—19]利用小波分析提取了SNR序列的瞬时频率，并利用瞬时频率来反演瞬时潮位。文献[18]中提到，利用小波分析方法可以探测有效瞬时频率消失的高度角，即多路径振荡消失的截止高度角。因此，本文将利用小波分析方法探测截止高度角，并研究截止高度角与风速之间的相关关系。

1 原 理

直射信号和反射信号会发生干涉，从而在SNR序列中表现出干涉振荡。在只考虑一次反射的情况下，低高度角、去除直射信号分量的残余SNR序列会呈现较为明显的干涉振荡，可以用式(1)表示[20]

(1)

式中，h为反射面到天线相位中心的高度，常被称为有效高度(reflector height,RH)，根据式(1)，h与振荡频率f之间的关系为h=(λf)/2；λ为信号波长；k=2π/λ；d为衰减因子；e为高度角；Amp为振幅。然而，在考虑到反射面并不光滑，存在粗糙度时，信号会存在散射现象。此时的残余SNR序列可以写为

(2)

式中，下标i表示第i个散射分量的相关参数；M为散射分量的总数；δSNRs可以写为相干分量(共性部分)δSNRcoh和非相干分量(非共性部分)δSNRincoh；相干分量表现为反射主导的分量，非相干量表现为噪声n，即式(2)可写为

δSNRscatter=δSNRcoh+δSNRincoh=Amp·

(3)

式中，当相干分量δSNRcoh更显著时，SNR序列表现有干涉振荡；当非相干量(噪声)δSNRincoh更显著时，SNR序列表现无干涉振荡。

1.1 散射模型

(4)

式中

ρ0=sin(vxX)sin(vyY)

vx=k(sinθd-sinθrcosφr)x

vy=k(sinθrsinφr)y

(5)

(6)

当eecutoff，非相干分量更显著，SNR振荡消失。根据式(6)，σh越大时，ecutoff越小；σh越小时，ecutoff越大。不同的σh会造成不同的ecutoff。从而，根据ecutoff，可以估计σh。

1.2 波浪模型

不同的风速会造成不同的海面粗糙度。海浪谱可以用来描述一定区域的海浪结构，它反映了各分量波的分布情况。若只考虑能量S相对于频率ω的分布，称一维谱或波浪频谱。根据Pierson-Moskowitz (P-M)波浪谱模型，波浪频谱为[23]

(7)

式中，g是重力加速度；U19.5是距海面19.5 m处的风速；Υ表示海浪随风速变化的响应程度因子。在成熟开阔海域条件下，Υ=1；在近岸海域，海浪处于破碎状态，可以根据海面情况调整Υ，0<Υ<1。利用P-M波浪谱仿真Υ=1和Υ=0.5时，不同风速下的σh；并根据该σh和式(6)计算对应的ecutoff，得到风速与ecutoff的对应关系。图1(a)给出了在理想开阔成熟海面(Υ=1)和理想散射条件假设下的风速与ecutoff之间的数据关系；图1(b)给出了在理想近岸海面(Υ=0.5)和理想散射条件假设下的风速与ecutoff之间的数据关系。可以看出，风速与ecutoff有单调递减的数学关系。

2 方 法

2.1 小波分析提取截止高度角

小波分析是一种通过对时间和频率进行局域变换，实现信号多尺度细化分析的方法，可以对序列的细节信号进行放大，起到“放大器”的作用[18-19]。设ψ(t)是基本小波函数，对于输入SNR序列δS(sin(e))，其小波变换为

(8)

式中，a和b分别是尺度缩放因子和平移因子。要获得小波分析结果，需要计算每个移位参数b的卷积，并对a重复此过程。MATLAB Wavelet Toolbox中的函数——centfrq和scal2frq，给出了a、b参数与频率的映射关系。得到频率后，根据h=(λf)/2(式(1))，将频率转换为RH。图2给出了HKQT站2018年DOY 258，PRN 1卫星的SNR序列、对应的小波分析谱图及根据谱图能量最大(峰值)选取的RH值，细节详见文献[18—19]。由于SNR噪声总是表现为高频噪声，所以有效RH值和噪声非常容易区分[18-19]。例如，图2中，当RH大于4时，认为是能反映海面变化的有效RH值，对应的SNR序列振荡明显，相干能量显著；当RH小于4时，认为是噪声信息，对应的SNR序列无明显振荡，非相干能量显著。即RH小于4的起始高度角，可以判定为多径振荡消失的截止高度角。文献[11]中，判定截止高度角的方法是基于最小二乘曲线拟合和特定阈值的；该方法对数据质量要求高且阈值需要根据经验确定，不同站点的阈值可能并不相同，方法较为复杂。而本文的小波分析判定方法，简单易行且不需要基于经验参数。

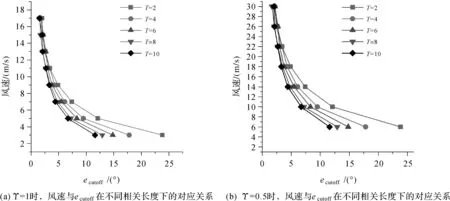
图1 风速与ecutoff在不同相关长度下的对应关系Fig.1 Relationship between ecutoff and wind speed with different T

图2 HKQT站2018年DOY 258，PRN 1卫星的SNR序列、小波谱图及峰值RH序列Fig.2 SNR sequence, wavelet spectrum and peak RH sequence of PRN 1 satellite on DOY 258 of 2018 for HKQT station

2.2 截止高度角基准统一

风速引起海面粗糙度变化，粗糙度引起截止高度角变化。理论上，风速越大，粗糙度越大，截止高度角越小；相反地，风速越小，粗糙度越小，截止高度角越大。这里用来描述截止高度角的越小或越大是一种定性描述，需要转换到定量描述。因此，本文构建了一个截止高度角变化量δecutoff，用以定量描述截止高度角的大小；δecutoff=ecutoff,wind_speed=1-ecutoff(其中，ecutoff,wind_speed=1为基准)，它描述的是以平静海面(风速为1 m/s)时的截止高度角为基准，ecutoff相对于基准的变化。图3给出了依据图1获得的δecutoff与风速之间的关系。图3(a)给出了在理想开阔成熟海面(Υ=1)和理想散射条件假设下的风速与δecutoff之间的数学关系；图3(b)给出了在理想近岸海面(Υ=0.5)和理想散射条件假设下的风速与δecutoff之间的数学关系。图3中，δecutoff与风速呈现指数函数的数学关系。

图3 风速与δecutoff在不同相关长度下的对应关系Fig.3 Relationship between δecutoff and wind speed with different T

在仿真试验中，反射面粗糙度变化是影响截止高度角的唯一因素。然而，在实际观测中，截止高度角与许多因素有关，其中包括粗糙度、反射率因子等反射面特性，也包括信号解调方式、信号频率、信号带宽等信号特性[24]。为了提高反演精度，需要保证粗糙度是影响截止高度角变化的唯一因素。由于GPS卫星的周期近似为1 d(11 h 58 min)，因此，同一卫星每天同一轨迹被接收机捕获的同一信号，理论上具有相同的反射区及相同的解调方式、信号频率、信号带宽；为了实现唯一变量影响，需要计算同一卫星同一信号同一轨迹的截止高度角的变化。同时，由于风速为1 m/s时的截止高度角在实际中并不容易获得，因此，选取同一卫星同一信号同一轨迹的截止高度角的均值作为基准，进而计算δecutoff。将第i个GPS卫星、第j个GPS信号，在第n天、第k轨迹获得的截止高度角记为ecutoffi,j,n,k，则定义该截止高度角对应第i个GPS卫星、第j个GPS信号、第k轨迹的δecutoffi,j,n,k为

(9)

图4 GNSS-IR风速反演Fig.4 GNSS-IR wind speed retrieval

3 算 例

3.1 站点及数据

站点HKQT(114.21°E，22.29°N)位于香港鰂魚涌，隶属香港卫星定位参考站网(https:∥www.geodetic.gov.hk/)，站点环境如图5(a)所示。接收机类型为TRIMBLE NETR5。该站可以接收多模多频GNSS信号的1 Hz采样的观测数据。考虑到反射区重返的问题，仅使用GPS数据进行风速反演。该站接收到的GPS信号有L1C/A、L2P、L2C及L5C；由于GPS L2P为加密信号，在信号解调过程中，容易引起一些GNSS-IR反演偏差[24-25]，故不在本算例中使用。根据文献[26]提供的基于Google Earth的反射区绘制工具，绘制反射区(图5(b))，根据水域范围，确定有效海域方位角[-60°,105°]；反射区相关原理参见文献[2,5,20]。考虑到平静水面条件下，截止高度角为25°～35°，因此，用于小波分析的数据弧段，选择高度角区域[5°,40°]。距离该站约1 km处，有一气象站点，编号为45 007，提供每小时一次的风速、降水等气象参数。同时，距离HKQT站点2 m处有一验潮站Quarry Bay可提供实测的潮位数据。为了验证GNSS-IR技术能否探测强风风速，算例时间选择了“天鸽”台风登港时间(2018年9月16日)前后日期2018年DOY 249—DOY 270，及“山竹”台风登港时间(2017年8月23日)前后日期2017年DOY 224—DOY 243。

3.2 风速反演结果

图6给出了2018年DOY 247—DOY 270间(台风“山竹”前后时间)的截止高度角变化参数与实测风速序列。图6(c)中，GPS L5C信号的截止高度角变化δecutoff与实测风速对应关系良好，相关系数达到0.85，高度相关。而图6(a)中，GPS L1C/A信号的截止高度角变化δecutoff与实测风速对应关系很差，相关系数仅为0.14，微弱相关；图6(b)中，GPS L2C信号的截止高度角变化δecutoff与实测风速对应关系一般，相关系数为0.40，低度相关。许多研究表明[24,27]，GPS L5C是GPS中信噪比质量最好的信号。而在该算例中，GPS L5C是δecutoff与风速相关性最好的信号。台风“山竹”在2018年9月7日于太平洋西北方位生成，2018年9月16日(DOY 258—DOY 259)台风向我国广东沿海逼近，2018年9月16日凌晨，香港处于台风风圈以内，一直持续到2018年9月16日中午。图6(c)中，在该时间内，实测风速剧增至32 m/s，截止高度角变化量剧增至18°；包括在风速攀升阶段，截止高度角也能很好地刻画风速在低风速至高风速下的变化情况。值得提出的是，在小于5 m/s的情况下，记录的风场信息，风向一直不稳定；这种不持续风向的风场条件会导致GNSS-IR风速探测的不准确。

图5 HKQT站Fig.5 HKQT station

图7给出了2017年DOY 224—DOY 243(台风“天鸽”前后时间)的截止高度角变化参数与实测风速序列。图7(c)中，GPS L5C信号的截止高度角变化δecutoff与实测风速对应关系良好，相关系数达到0.70，高度相关。而图7(a)中，GPS L1C/A信号的截止高度角变化δecutoff与实测风速对应关系很差，相关系数仅为0.05，不相关；图7(b)中，GPS L2C信号的截止高度角变化δecutoff与实测风速对应关系一般，相关系数为0.42，低度相关。在该算例中，GPS L5C是δecutoff与风速相关性最好的信号。台风“天鸽”在2017年8月20日于太平洋西北方位生成，受其影响，香港局部区域于2017年8月23日(DOY 234—DOY 235)遭受10级大风。图7(c)中，在该时间内，实测风速剧增至23 m/s，截止高度角变化量剧增至16°。除去台风期间，香港2019年8月26日(DOY 238)持续有3～4级东风，在该时间内，实测风速增至15 m/s，截止高度角变化量剧增至10°。同时，在风速攀升阶段，截止高度角也能很好地刻画风速在低风速至高风速下的变化情况。在小于5 m/s的情况下，记录的风场信息，风向一直不稳定；这种不持续风向的风场条件会导致GNSS-IR风速探测的不准确。

图6 HKQT站2018年DOY 250—DOY 270 δecutoff序列与实测风速序列Fig.6 δecutoff vs. measured wind speed during DOY 250 and DOY 270 of year 2018 for HKQT station

图7 HKQT站2017年DOY 225—DOY 243 δecutoff序列与实测风速序列Fig.7 δecutoff vs. measured wind speed during DOY 225 and DOY 243 of year 2017 for HKQT station

为了更好地比较截止高度角变化δecutoff与风速的关系，图8给出了GPS L5Cδecutoff与风速之间的对应关系。由于GPS L1C/A与GPS L2C信号δecutoff与风速之间的相关性较低，故未在图8中分析。图8表明，δecutoff与风速之间存在一种近似指数函数的变化；图8中的风速s与δecutoff的拟合指数函数(拟合函数的RMSE为3.09 m/s)为

s=f(δecutoff)=3.70×e0.12×δecutoff

(10)

同时，2018年和2017年不同时间段内的函数关系相同。这说明，同一个站点，δecutoff与风速之间的数学对应关系是一定的。该数学关系与图3(b)中T=4时根据仿真获得的数学关系近似。因此，在对海面情况进行调查后，可以根据散射模型和波浪谱模型获得δecutoff与风速之间的数学关系，再通过实测的δecutoff，反推获得相关的风速值。

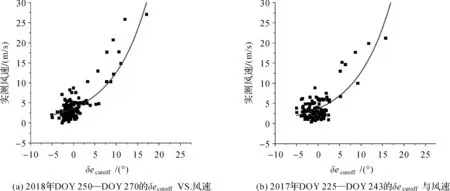
图8 HKQT站δecutoff与风速Fig.8 δecutoff VS. measured wind speed at HKQT station

4 结论与讨论

本文提出了一种基于小波分析的GNSS-IR风速反演方法，通过算例证实了δecutoff与风速存在特定的指数函数关系，证实了利用GNSS-IR技术进行风速探测的可能性，扩充了GNSS-IR的监测对象，拓宽了GNSS-IR的应用范围。地基GNSS-IR风速反演和星载GNSS-R风速反演的方法不同，但是核心相同——风速会造成不同的海面粗糙度，使反射信号特性不同；从而可以利用反射信号的特性反推粗糙度，进而反推风速。为了保证风速反演的准确性，需要尽量保证风速是引起粗糙度的唯一因素，这就对站点的海面环境提出了要求。对于海面变化剧烈(如潮位振幅较大或者有船行波影响)的站点，本身海面的粗糙度就较大，理论上是无法进行风速反演的；对于某些粗糙度的变化主要为风导致(一般海面变化较小)的站点，GNSS-IR风速反演技术理论上可用。

值得注意的是，利用截止高度角参数、基于波浪谱模型和散射模型的仿真在文献[17](研究粗糙度及有效波高反演)中均已提及。本文的贡献主要在：

(1) 使用了更好的截止高度角参数提取方法——小波分析，来反演风速。

(2) 提出了截止高度角基准统一方法。文献[17]认为不同卫星不同轨迹相同信号的截止高度角的基准相同；而经过算例分析，本文发现不同卫星不同轨迹相同信号的截止高度角的基准不同。文献[17]认为基准相同，可能是由于文献[17]中的试验区域环境极好(站点很高、海域开阔、四面环海)，不同轨迹的反射区环境大致相同导致。而本文算例中的站点环境更为常见，所用的截止高度角基准统一方法适应性更强。

(3) 证实了GNSS-IR技术可以监测风速。

本文只是GNSS-IR探测风速的初步探索，想要推进该技术的实际应用，还需要对下列问题进行研究。

(1)δecutoff与风速之间的数学关系。根据理论，式(10)所得到的数学关系，仅适用于附近海域(或相似特性的海域)及GPS L5C信号，对于其他特性的海域及其他信号并不适用。数学关系的准确与否决定了能否根据δecutoff获得准确的风速参数。该数学关系与海面特性(主要指海面粗糙度随风速的变化情况)及信号特性(包括信号调制和解调方式、信号频率等)有关。数学关系的建立可以从两方面入手。①使用更好的波浪谱模型，得到更好的仿真数学关系。目前效果比较好的波浪谱模型大都基于成熟广阔的海域。本文所用到的沿岸波浪谱是最简单的波浪谱，并不准确。实际上，沿岸波浪受海洋深度、海洋特性、沿岸海岸线、风速风向等影响，相关波浪谱的建立十分复杂。波浪谱模型的准确建立，对于建立δecutoff与风速之间的数学关系非常重要。②根据大量实测数据，建立数学关系。由于利用仿真建立的数学关系是基于理想情况下，可能与实际情况不符。在大量算例的支撑下，可以根据大量实测δecutoff和实测风速数据，利用拟合方法或神经网络方法，建立二者之间的数学关系；从而根据任一站点的实测δecutoff推算风速。

(2) 风速反演阈值的研究。风速反演必然存在上限，即，对于大于某一特定上限的风速，GNSS-IR方法无法探测。在上限风速情况下，引起的海面粗糙度已经使截止高度角达到最低(本文为5°)。上限风速与信号特性、信号解调方式、海面特性等有关。对于本算例用到的站点情况，上限风速在25 m/s～30 m/s。

(3) 信号研究。本文的算例表明，GPS L5C可用，而GPS L1C/A、GPS L2C信号并不可用。但是在某些环境较好的情况下(站点较高、海域开阔)，GPS L1C/A、GPS L2C信号也可能能够反映风速变化。需要相关研究，以获得不同信号在不同环境下的截止高度角参数与风速之间的数学关系。

另外，本文提出的相关理论和方法除了进行风速反演外，还隐藏着另一个重要的潜在应用——推算波浪特性。波浪特性对于海岸工程建设十分重要，波浪资料的获得目前主要依赖于浮标；而浮标站点数量有限，监测范围小。根据本文的理论及试验，在有实测风速的情况下，根据SNR的δecutoff值，可以绘制δecutoff与风速图(如图8所示)；而根据不同的风速波浪谱，可以得到不同的仿真δecutoff与风速图(如图1及图3所示)；将实际δecutoff与风速图与仿真δecutoff与风速图进行对比，根据符合程度，可以推算该地区在风速影响下的波浪特性。例如本文根据实测图8及仿真图3，得到HKQT站点附近海域的海浪表现近似为T=4，Υ=0.5时P-M波浪谱模型(式(7))。今后，本团队将继续研究GNSS-IR波浪特性反演的相关理论和方法，并挖掘GNSS-IR其他潜在应用。