Design of off-axis multi-reflective optical system based on particle swarm optimization

WU Yue，WANG Li-ping，YU Jie，ZHANG Xu，JIN Chun-shui

（1.Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences,Changchun 130033, China；2.University of Chinese Academy of Sciences, Beijing 100039, China）

Abstract: An initial construction satisfying aberration balance and multi-constraint control is essential for the design of an off-axis multi-reflective optical system with minimal aberration.In this paper, a mathematical model for calculating the initial structure of off-axis multi-reflective is established based on the grouping design method combining spatial ray tracing and aberration correction, and an improved Particle Swarm Optimization (PSO) is proposed to solve the initial structure problem of an off-axis multi-reflective optical system.The PSO of natural selection with shrinkage factor is applied to improve calculation accuracy and design efficiency, so as to obtain the initial structure of the off-axis multi-reflection optical system.In the last part of this paper, taking an Extreme UltraViolet (EUV) lithography projection objective with six-mirror reflective aspheric mirrors as an example, the reliability and effectiveness of this method are verified.A 0.33 numerical aperture EUV lithographic objective with wave-front error better than 1/80λ (λ=13.5 nm) RMS is achieved.

Key words: optical design; geometric optics; aberration theory; particle swarm optimization

1 Introduction

Compared with refractive optical systems, reflective optical systems have the following advantages: reflective optical systems do not produce chromatic aberration; their optical path can be folded,which facilitates the shortening of the barrel length to make the structure compact; they are relatively insensitive to changes in temperature and air pressure; they effectively solve the obstruction constraint by off-axis eccentric tilt, which is conducive to increasing the field of view and improving the image quality.Therefore, the design of off-axis reflective optical systems has received extensive attention, and is often used in space cameras, telescopes, and infrared/ultraviolet fields[1-5].In recent years, off-axis six-mirror reflective EUV lithography projection objectives have become a typical application of off-axis multi-reflection optical systems.EUV lithography projection objective has extremely high imaging requirements, which needs to achieve super diffraction limit resolution and the wave aberration better than 1/50λ[6-9].The design of optical systems to achieve ultra-diffraction-limited minimum aberrations depends heavily on aberration balance.It needs to solve the contradiction among the multi-constraint, multi-objective and few degrees of freedom, which brings great challenges to optical designers.The current optical design software mainly solves the optimization problem of optical systems by using the damped least squares local optimization algorithm to calculate the minimum of the error function in the multi-dimensional variable space, and the final optimization result is in most cases a local optimal solution close to the initial structure, which has great limitations[10], and its global optimization function is difficult to achieve aberration balance and constraint control simultaneously in the case of poor initial structure.Optimal design using optical design software relies heavily on the selection of the initial structure, and the initial structure construction is the key to optical system design[11].Especially for minimal aberration optical systems, which are more sensitive to the aberration balance, the construction of the initial structure to satisfy the aberration balance and multi-constraint control is a key issue in order to balance the constraint and aberration and to avoid the optical system perturbation too large, which makes it difficult to realize the minimal aberration optical system.

At present, the common initial structure construction methods of reflective optical systems include paraxial search method, Y, Y-bar method and group design method.Among them, the paraxial search method was proposed by M.F.Bal, which uses a paraxial model to exhaustively enumerate the first-order aberrations of the optical system.The number of constraints that can be met is too small,which greatly affects the efficiency[12-13].Scott A.Lerner et al.applied the Y, Y-bar method to the solution of the optical system structure, which uses the height of the marginal rays and chief rays on the surface of the optical element to solve the radius of curvature and the distance between the mirrors to construct the initial structure.The height of chief ray and marginal ray of the optical surface of each structure is not easy to determine, and it is not universal.When the number of off-axis reflective optical system components is large, the calculation amount of the above method will increase greatly,which affects the design efficiency[14-15].The grouping design method was applied to the design of offaxis six-mirror reflective optical system by Hudyma.The optical system was divided into two groups, but he did not give a specific design method[16].The research group of Professor Li Yanqiu of Beijing Institute of Technology proposed a real ray-tracing grouping design method applied to off-axis six-reflector and more multi-part reflector systems, by which the off-axis reflector optical system is divided into three groups, the structural parameters of each mirror group are determined by real ray-tracing calculation based on constraint control,and finally the structural parameters of the three mirror groups are spliced[17-18].The above methods have not yet solved the following problems: (1) the optimization process may produce large disturbances, and the structure deviates too much from the initial structure, making the constraints difficult to control; (2) optical design software optimization in the aberration balance process of low-order aberration and high-order aberration may appear large residuals, thus making the optical system design residuals large, which is not conducive to the realization of minimal aberration system.

In order to solve the problem of aberration balance and multi-constraint control in the process of initial structure construction, a mathematical model of off-axis multi-reflection initial structure calculation is established in this paper based on the grouping design method combining spatial ray tracing and aberration correction[19].The Particle Swarm Algorithm (PSO) is used to calculate and solve the high-dimensional nonlinear mathematical model.Several common hybrid PSOs are compared.The proposed PSO with natural selection and shrinkage factor improves the computational accuracy and design efficiency, and provides a design fundation for the design of off-axis multi-reflection optical systems with minimal aberration optimization potential.In this paper, the above method is applied to the EUV lithography projection objective optical system to realize the design of the off-axis six-mirror reflective minimal aberration optical system,whose main design process includes: (1) divide the optical system into two groups, namely the objectside mirror group and the image-side mirror group;(2) based on the aberration theory and space ray tracing theory, parameterize the structural parameters of the optical system, establish mathematical models for the calculation of the corresponding parameters for the front and rear mirror groups, and join the front and rear mirror groups to obtain the mathematical models of the initial structure; (3) the traditional PSOs are compared horizontally, a natural selection PSO with shrinkage factor is proposed to calculate and solve the initial structure parameters; (4)optimize the initial structure.Use the incremental optimization method to avoid excessive changes in the system structure during the optimization process and deviation from the initial structure.Finally,an off-axis six-mirror reflective optical system with engineering feasibility is realized, and its integrated system wave aberration is close to 1/80λ RMS.

2 Mathematical model for initial structure calculation

2.1 Grouping design method

As shown in Figure 1, in this paper, the off-axis six-mirror reflective EUV lithography objectives are divided into two groups, the object-side mirror group and the image-side mirror group, and the optical paths of the first near-axis ray and the second near-axis ray are calculated.The parameters of the optical system mainly include the miniaturization magnification of the system asβ, the center height of the object-side field of view asy, the center height of the image-side field of view asyim, the numerical aperture of the object-side asNAO, and the numerical aperture of the image-side asNA.Then we can getyim=y·β,NAO=NA·β.The object-side mirror group and the image-side mirror group are spliced at the intermediate image, and the splicing should ensure that the object image matches, the pupil matches and the magnification matches.Based on the above principles, the structural parameters of the object-side mirror and image-side mirror of the optical system are parameterized, the spatial ray tracing is introduced, and the constraint parameters of the optical system, such as blocking, mirror spacing,image apocenter, aperture and incident angle, are quantified to establish a mathematical model for the calculation of the initial structural parameters of the minimal aberration off-axis six-mirror reflective EUV lithography objective.

Fig.1 Schematic diagram of the Off-axis six-mirror reflective optical system structure图1 离轴六反光学系统结构示意图

2.2 Aberration analysis of the object-side mirror group (Group 1)

As shown in Figure 2, the height of the center of the field of view on the object side isy, the aperture angle of the object side isu1, and the diaphragm is located at M2.The light starts from the object field of view and reaches the intermediate image point through M1, M2, M3, M4. Among them,d1,d2,d3,d4respectively represent mirror pitch from M1to M2, mirror pitch from M2to M3, mirror pitch from M3to M4, and the distance from M4to the middle the image point IM;h1,h2,h3,h4denote the heights of the first auxiliary rays on M1, M2, M3, M4,respectively;r1,r2,r3,r4andk1,k2,k3,k4denote the radius of curvature and quadratic surface coefficients of M1, M2, M3, M4, respectively;l1,l2,l3,l4andare the object and image distances of M1, M2,M3, and M4, respectively.

Fig.2 Group 1 structure schematic diagram图 2 Group 1结构示意图

The third-order monochromatic aberrations mainly include spherical aberration, comatic aberration, astigmatism, curvature of field, and distortion,which are represented bySI,SII,SIII,SIV,SVrespectively, and the formula is[4,20]:

Based on paraxial approximation conditions,following parameters are introduced:

For this reflection system,

For the ray tracing of the paraxial chief ray and the paraxial marginal ray, the following formula is obtained:

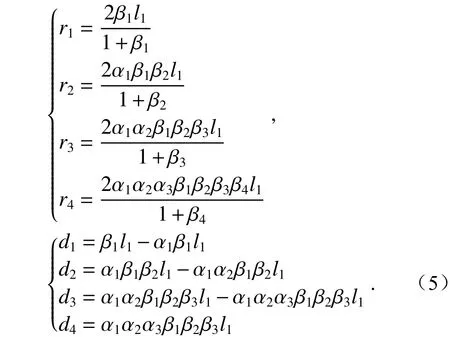
The distance between the exit pupil position and M4in Group 1 is

Substituting formula (2−4) into (1), the G1 aberration coefficient of the front lens group can be calculated.

2.3 Aberration analysis of the image-side mirror group (Group 2)

As shown in Figure 3, in the image-side mirror group, the height of the object-side field of view center isy5, the height of the image-side field of view center isyim, the object-side aperture angle isu5.The light starts from the intermediate image point and reaches the image point through M5and M6, whered5andd6denote the mirror distance from M5to M6and the distance from M6to the image plane, respectively;h5andh6denote the height of the first auxiliary ray on M5and M6, respectively;r5,r6andk5,k6denote the radius of curvature and quadratic surface coefficient of M5and M6, respectively;l5,l6, andl′5,l′6are the object distance and image distance of M5and M6, respectively.

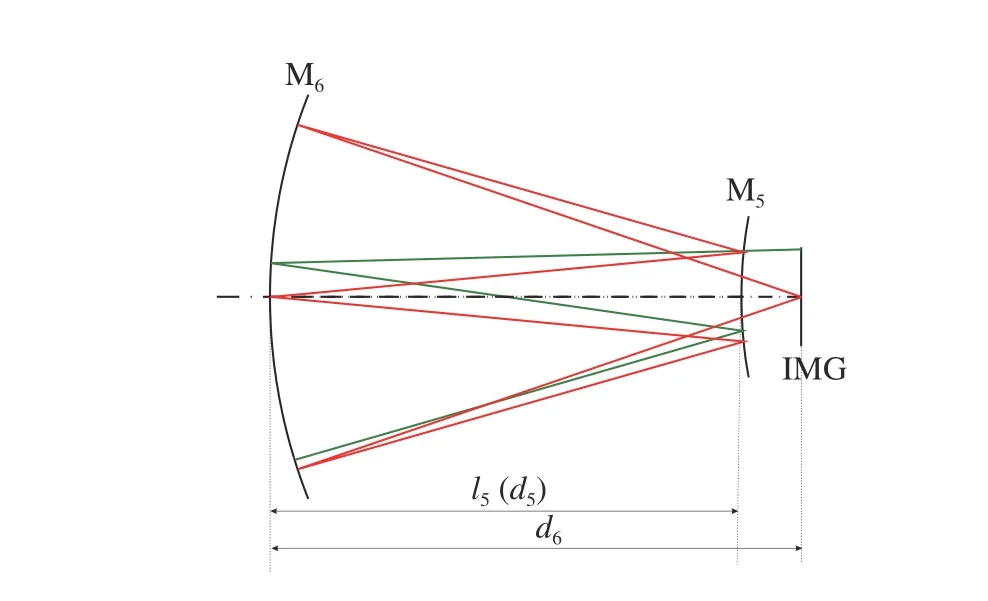
Fig.3 Schematic diagram of the Group 2图 3 Group 2示意图

Similarly, parameters are introduced based on paraxial approximation conditions:

For this reflection system,

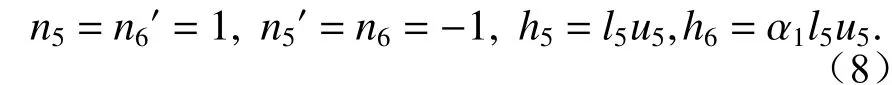
Perform ray tracing on the paraxial chief ray and the marginal ray to obtain the following formula:

The distance between the entrance pupil position and M5in Group2 is

According to the optical pupil matching condition, namely, the outgoing pupil of G1 coincides with the incoming pupil of G2.Through calculation,we can get the distance between the entrance pupil position and M5in Group1 is

Substituting the formula (7−8) into (1) to obtain the aberration coefficient of the rear lens group G2.

2.4 Mirror group splicing and mathematical model establishment

According to the splicing principle, which mainly includes object image matching, magnification matching and optical pupil matching, the following function can be derived after splicing the object-side mirror group and the image-side mirror group:

The aberration of the coaxial optical system satisfies the linear superposition, that is, the aberration of the entire optical system is the sum of the aberration contributions of each element in the optical system.Therefore, the aberration coefficient of the off-axis six-mirror reflective optical system is the sum of the aberration coefficients of Group 1 and Group 2, and the aberration coefficient of the optical system can be obtained by solving the aberration coefficients of the two lens groups.

Through the above aberration theory, the thirdorder aberration coefficient and structural parameters of the EUV lithography objective optical system are calculated.In order to meet some special requirements of the optical system, spatial optical tracing is also introduced, and the special requirements of the optical system are taken as constraints which can effectively control the constraints such as occlusion, mirror spacing, aperture, image side telecentricity, and incident angle during the construction of the initial structure.Based on the above constraints and according to the objective, i.e., the thirdorder aberration coefficient is as small as possible,the evaluation function can therefore be written as

where constraints represent the above mentioned constraints.The evaluation functionFreflects the size of the primary aberration of the optical system and the constrained control ability.The smaller the value, the smaller the primary aberration of the initial structure, the better the aberration control of the structure, and the bigger the potential for achieving high imaging quality.In this paper, through aberration theory and constraint control, a mathematical model of off-axis six-mirror reflective parameter design with minimal aberration is established, and the physical model is transformed into a mathematical model, which is the problem of solving high-dimensional nonlinear parameter equations.

3 Using PSO to calculate and solve the mathematical model of off-axis six-mirror reflective initial structure

At present, the main algorithm for calculating the initial structure of the optical system structure is the genetic algorithm[11,21-22].The genetic algorithm based on biological evolution has good global search capabilities.Because of its inherent parallelism, multiple individuals comparison can be carried out at the same time, and its scalability makes it easy to combine with other algorithms.However,the poor local search ability of genetic algorithm results in low search efficiency of genetic algorithm and a certain dependence on the selection of the initial population.PSO was proposed by Eberhart and Kennedy in 1995[23].The advantage of this algorithm lies in the simplicity, ease of implementation, versatility, and speed of calculation, and does not require gradient information.It is an effective optimization tool for nonlinear optimization problems, combinatorial optimization problems, and mixed-integer nonlinear optimization problems.It is currently widely used in application fields such as function optimization, neural network training, and practical engineering.The basic PSO algorithm also has certain shortcomings.When dealing with highdimensional complex problems, the algorithm tends to fall into local values; when the problem scale is large, the algorithm convergence speed is slower and the accuracy is limited.In order to overcome the deficiencies of the basic PSO algorithm, the current related improvements mainly include parameter improvement and hybrid algorithm.Parameter improvement is mainly through the introduction of some new parameters, but this also increases the complexity of the algorithm to a certain extent while improving the algorithm, including the PSO algorithm with improved weight, the PSO algorithm with shrinkage factor, and the PSO algorithm with variable learning factor.Hybrid algorithm is the hotspot of PSO algorithm improvement.Combining other algorithms in PSO algorithm improves the global search ability and search accuracy of PSO algorithm, including PSO algorithm based on natural selection, PSO algorithm based on hybridization,PSO algorithm based on simulated annealing, etc.[24-25].

Because the learning factorsc1andc2determine the influence of the particle's own experience information and the experience information of other particles on the particle trajectory, they reflect the information exchange between particle swarms.Whenc1is set larger, the particles will linger too much in the local area, whenc2is set larger, the particles will converge to the local minimum prematurely.In order to effectively control the flying speed of particles so that the algorithm achieves an effective balance between global detection and local mining, Clerc constructed a PSO algorithm that introduces a shrinkage factor to ensure the convergence of the PSO algorithm, and can cancel the boundary limit on the speed, which can effectively control the flight speed of constrained particles and enhance the local search capability of the algorithm.

In this paper, a natural selection PSO with shrinkage factor is proposed to construct the mathematical model of the initial structure of the off-axis six-mirror reflective optical system.The above three hybrid PSO algorithms are compared horizontally, and the shrinkage factor are introduced into the simulated annealing PSO algorithm and the hybrid PSO algorithm, and the natural selection PSO algorithm with inertia weight is introduced for comparison.Since the condition for introducing shrinkage factor isc1+c2> 4.Setc1+c2=4.1 in Clerc's method with shrinkage factor.Figure 4 shows the convergence curves of the four algorithms under 6 groups of different learning factors, wherec1+c2=4.1 in the group 1−5, andc1+c2= 4.3 in the sixth group, the number of particlesN=1000, the maximum number of iterations is 100, the annealing constant is 0.42, the hybridization probability is 0.9, the size ratio of the hybridization pool is 0.2, and the inertia weight factor is 0.7.The minimum evaluation function values calculated by the four algorithms with six groups of learning factors are given in Table 1, respectively.From Figure 4 and Table 1, it can be seen that for the above 6 groups of different learning factors, the natural selection PSO with shrinkage factors has a great improvement in the calculation accuracy and the convergence speed of the mathematical model of the initial structure of the off-axis six-mirror reflective optical system and which provides a design fundation for the design of the off-axis six-mirror reflective optical system with minimal aberration optimization potential.

The main process of the natural selection PSO with shrinkage factor is shown in Figure 5: Step 1:establish a mathematical model for calculating the initial structure of the off-axis six-mirror reflective optical system, and initialize the position and velocity of the particles in the population randomly.Step 2: evaluate the fitness of each particle, store the current position and fitness value of each particle in the individual extreme value of each particle, calculate the individual extreme value and the global optimal value, where for each particle the individual extreme value is found, from which a global value is to found, which is called the global optimal solution.Step 3: based on the shrinkage factor, update the speed and position of each particle.Step 4: according to the fitness value, update the individual extreme value and the global optimal solution among the particles.Step 5: sort the entire particle swarm by fitness value, replace the position and velocity of the worst half with the velocity and position of the best half of the particles in the swarm, and keep the individual extreme value and the global optimal solution unchanged.Step 6: if the termination condition is met (the error is good enough or the maximum number of cycles is reached), the cycle ends,otherwise it returns to Step 3.Step 7: solve the offaxis six-mirror reflective initial structure with minimal aberration according to the calculation result of the algorithm.

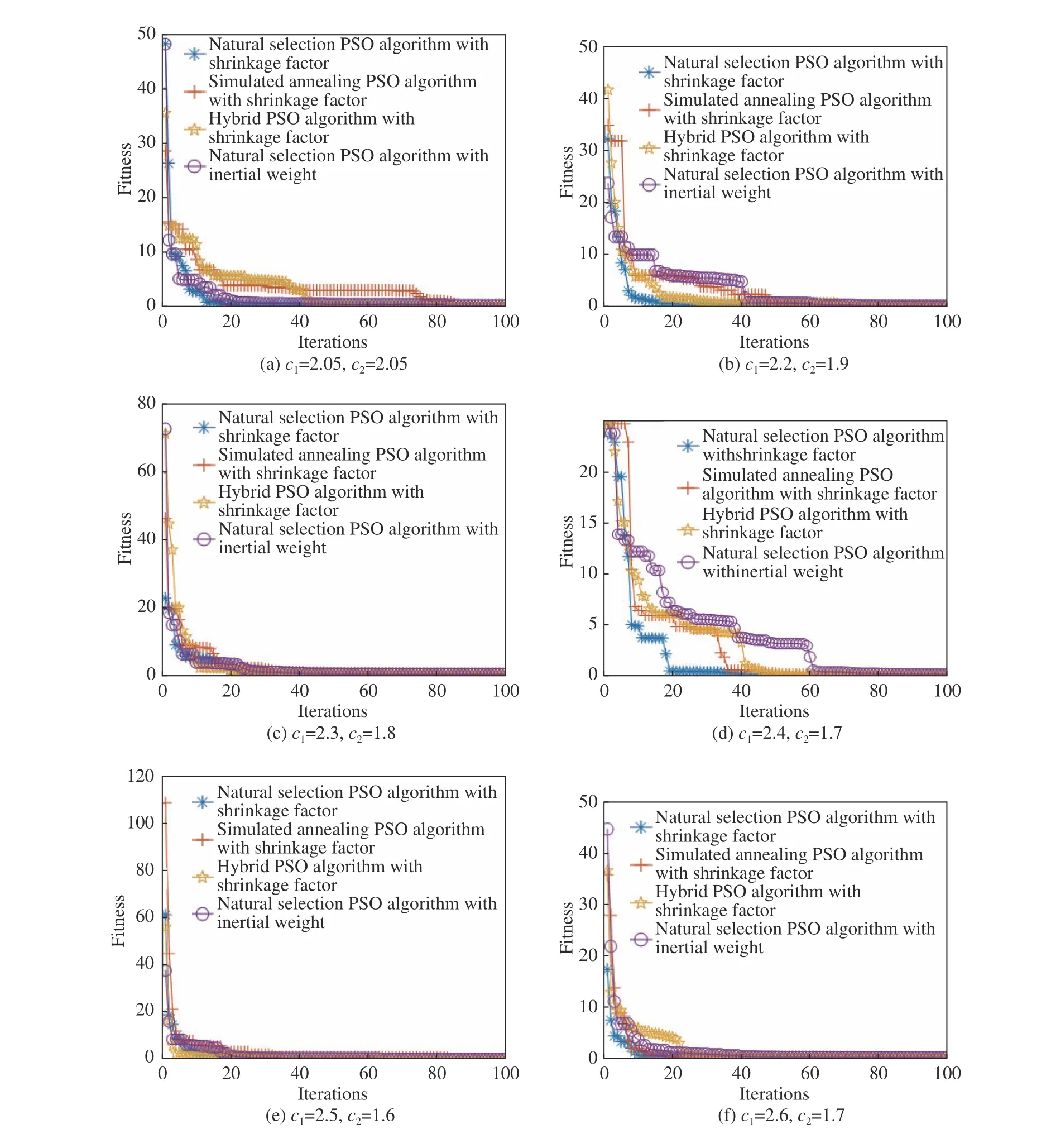
Fig.4 Convergence curves of evaluation functions calculated by four different algorithms for 6 groups of learning factors图4 针对6组学习因子4种不同算法计算的评价函数的收敛曲线图

Tab.1 Evaluation function values calculated by four different algorithms for 6 groups of learning factors表1 6组学习因子4种不同算法计算的评价函数值

Fig.5 Flow chart of the proposed algorithm图5 算法流程图

The initial structure of the off-axis six-mirror reflective optical system is solved by the natural selection PSO with shrinkage factor.The initial structure diagram is shown in Figure 6.

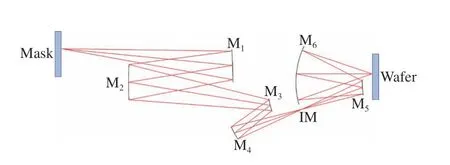
Fig.6 Schematic diagram of initial structure for the off-axis six-mirror reflective optical system图6 离轴六反光学系统初始结构示意图

4 Optimal design

We optimize the design of the above initial structure.At the beginning of the optimization, a high-order aspheric coefficient is added to the quadric surface shape to obtain high imaging quality.The constraints in the solution of the initial structure (mirror spacing, no obstruction, incident angle,mirror aperture, telecentricity, asphericity, etc.) are not destroyed, so that the optimized result has a small deviation from the initial structure, and the disturbance is controlled during the optimization process (If it is too large, the extreme value will be skipped, if it is too small, the result will fall into a local minimum).

Based on the above-mentioned initial structure solution and optimization principles, the design of an off-axis aspheric six-mirror reflective optical system with minimal aberration is realized.Figure 7 shows the design results of the off-axis six-mirror reflective optical system, and the specific parameters are shown in Table 2.The total working distance is 1371 mm, the rear working distance is 38 mm, and the image-side field of view is an arc field of view of 26 mm×2 mm.The maximum asphericity of the component is 60 μm, and the maximum distortion of the full field of view of the off-axis sixmirror reflective optical system is 1 nm, and the distortion distribution of the full field of view is shown in Figure 8 (Color online).The comprehensive wave aberration of the full field of view is 0.011λ RMS,its full field of view wave aberration distribution is shown in Figure 9 (Color online).According to the above design results, the design satisfies the constrained control while achieving extremely low aberration, making the EUV lithography objective lens system more engineering realizable.

Fig.7 Schematic diagram of the optimized structure for the off-axis six-mirror reflective optical system图7 极小像差离轴六反光学系统优化后结构示意图

Fig.8 Distortion on full image field for the off-axis sixmirror reflective optical system图8 离轴六反光学系统全视场畸变分布图

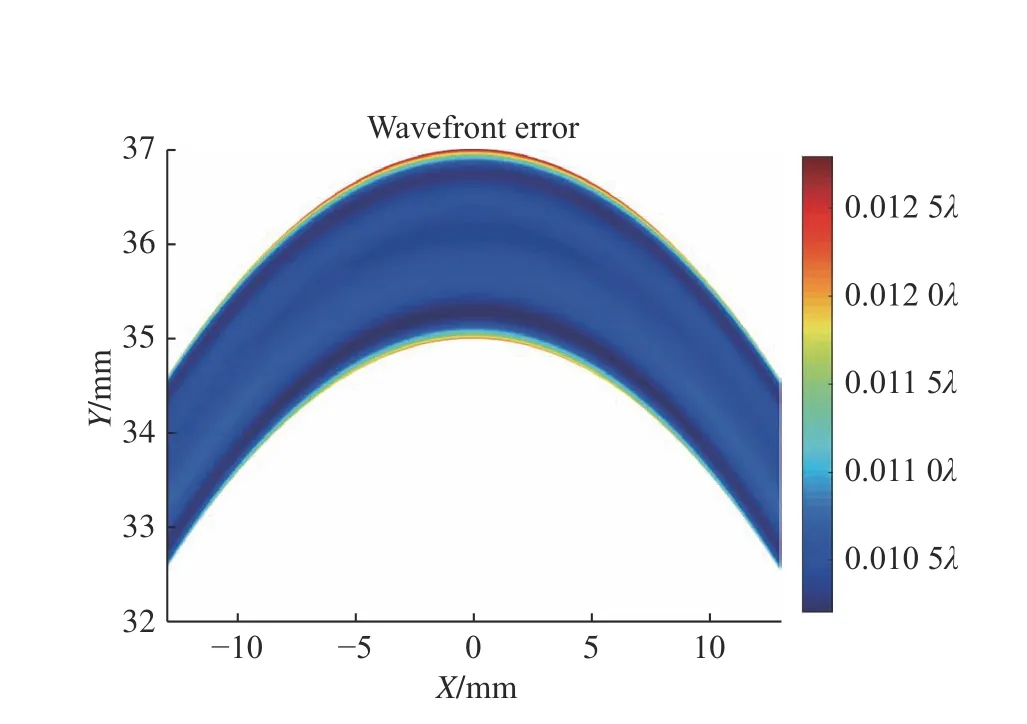
Fig.9 Wavefront error RMS on full image for the off-axis six-mirror reflective optical system图9 离轴六反光学系统全视场波像差分布图

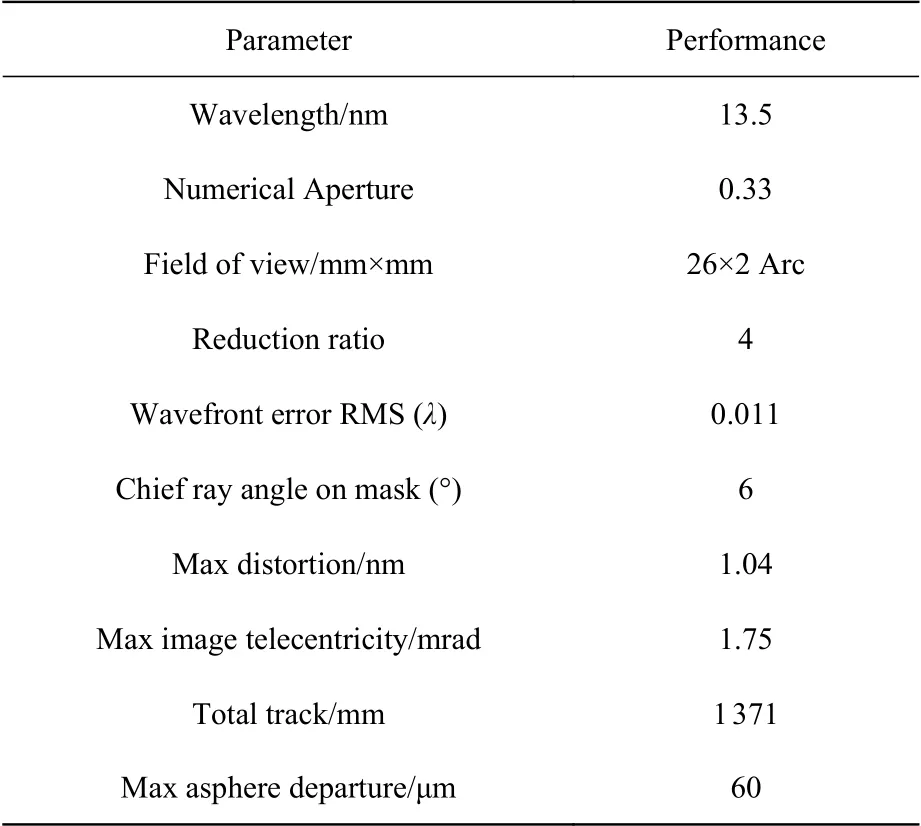
Tab.2 Specifications of the off-axis six-mirror reflective optical system表2 离轴六反光学系统设计主要参数指标

5 Conclusion

In order to solve the problem of aberration balance and multi-constraint control in the process of initial structure construction, a mathematical model of the initial structure calculation of off-axis sixmirror reflective is established based on a grouping design method combining spatial ray tracing and aberration correction.In this paper, the solution accuracy and design efficiency are improved by using the natural selection PSO with shrinkage factor, and a design fundation for off-axis six-mirror reflective optical system with minimal aberration optimization potential is provided.Using this method, the design of an off-axis six-mirror reflective optical system with minimal aberration is realized, and its comprehensive wave aberration of the full field of view is 0.011λ RMS.

The method proposed in this paper can be extended to off-axis multi-reflective optical systems,which can be used to design the off-axis multi-reflective initial structures with aberration balance and multi-constraint control capabilities, providing a design fundation for off-axis multi-mirror reflective optical systems with the potential for optimization of extremely low aberration.

——中文对照版——

1 引言

与折射光学系统相比，反射光学系统具有以下优势：反射光学系统不产生色差；光路可折叠，便于缩短筒长使结构紧凑；对温度和气压的变化相对不敏感；通过离轴偏心倾斜有效解决遮拦约束，有利于增大视场，提升像质，因此离轴反射式光学系统的设计受到了广泛关注，常应用于空间相机、望远镜以及红外/紫外等领域[1-5]。近年来，离轴六反极紫外光刻投影物镜是离轴多反光学系统的一种典型应用。极紫外光刻投影物镜成像要求极高，需要实现超衍射极限分辨率，波像差优于1/50λ[6-9]。实现超衍射极限极小像差光学系统设计，非常依赖于像差平衡，需要解决多约束、多目标与少自由度矛盾，这给光学设计人员带来极大挑战。目前光学设计软件主要解决光学系统优化问题，采用阻尼最小二乘法的局部优化算法，计算多维变量空间误差函数的最小值，最终优化结果大多数情况下是离初始结构较近的局部最优解，有着很大的局限性[10]，其全局优化功能在初始结构不佳的情况下，难以同时实现像差平衡与约束控制，利用光学设计软件优化设计严重依赖于初始结构的选择，初始结构构建是光学系统设计的关键[11]。尤其是对于像差平衡更为敏感的极小像差光学系统，为了在优化过程中平衡约束与像差使得光学系统扰动过大，难以实现极小像差光学系统，满足像差平衡和多约束控制的初始结构构建是关键问题。

目前，常见的反射式光学系统初始结构构造方法有近轴搜索法和Y，Y-bar方法以及分组设计方法。其中，近轴搜索法是由M.F.Bal提出的，该方法采用近轴模型，对光学系统的一阶像差进行穷举，能够满足约束要求的数量太少，极大影响效率[12-13]。Scott A.Lerner等人将Y，Y-bar方法应用到光学系统结构求解上，该方法是利用边缘光线和主光线在光学元件表面的高度求解曲率半径和镜间距来构建初始结构。每一种结构的光学表面的主光线和边缘光线高度并不容易确定，不具备普适性。对于离轴反射光学系统元件数目大时，上述方法的计算量将大幅增加，影响设计效率[14-15]。分组设计方法由Hudyma应用于离轴六反光学系统设计，他将光学系统分为两组，但并没有给出具体设计方法[16]。北京理工大学李艳秋教授课题组提出真实光线追迹的分组设计方法应用于离轴六反及更多元件数的反射系统，该方法将离轴反射光学系统分成3组，基于约束控制通过真实光线追迹计算确定每个镜组的结构参数，最后将3个镜组结构参数进行拼接[17-18]。上述方法尚未解决以下问题：（1）优化过程可能会产生较大的扰动，结构偏离初始结构过大，使得约束难以控制；（2）光学设计软件优化中像差平衡过程低阶像差与高阶像差可能出现较大的残余量，使得光学系统设计残差大，不利于实现极小像差系统。

为了解决初始结构构建过程中像差平衡和多约束控制问题，本文基于空间光线追迹与像差矫正相结合的分组设计方法，建立了离轴多反的初始结构计算的数学模型[19]，采用粒子群算法对该高维非线性数学模型进行计算求解，横向对比了几种常见的混合粒子群算法，提出带收缩因子的自然选择的粒子群算法提高了计算精度，提升了设计效率，为离轴多反光学系统设计具备极小像差优化潜力提供设计起点。本文将上述方法应用于极紫外光刻投影物镜光学系统中，实现离轴六反极小像差光学系统设计，其主要设计流程为：（1）将光学系统分为两组，即物方镜组与像方镜组。（2）基于像差理论与空间光线追迹理论，将光学系统的结构参量参数化，针对前后镜组，分别建立相应的用于参数计算的数学模型，将前后镜组拼接，获取初始结构计算数学模型。（3）横向对比传统的粒子群算法，提出了带收缩因子的自然选择的粒子群算法计算求解初始结构参数。（4）优化初始结构。利用渐进式优化方法，避免优化过程系统结构变化过大，偏离初始结构。最终实现了具备工程可实现的离轴六反光学系统，其综合系统波像差接近1 /80λRMS。

2 初始结构计算的数学模型

2.1 分组设计方法

如图1所示，将离轴六反极紫外光刻物镜分成两组，即物方镜组和像方镜组，分别计算第一近轴光线和第二近轴光线的光路。光学系统参数主要包括系统的微缩倍率β，物方视场中心高度y，像方视场中心高度yim, 物方数值孔径NAO，像方数值孔径NA。则可以得出yim=y∙β，NAO=NA∙β。物方镜组与像方镜组在中间像处拼接，拼接时应保证物像匹配，光瞳匹配以及倍率匹配。基于上述原则，将光学系统的物方镜组和像方镜组的结构参量参数化，引入空间光线追迹，将光学系统中的遮拦、镜间距、像方远心、口径以及入射角等约束参量化，建立极小像差离轴六反极紫外光刻物镜 初始结构参数计算的数学模型。

2.2 物方镜组（Group 1）像差分析

如图2（彩图见期刊电子版）所示，物方视场中心高度为y，物方孔径角为u1， 光阑位于 M2处。光线从物方视场出发，经 M1、 M2、M3、M4到达中间像点。其中d1、d2、d3、d4分 别表示M1到 M2的镜间距、 M2到 M3的 镜间距、 M3到M4的镜间距、M4到 中间像点IM的距离；h1、h2、h3、h4分别表示第一辅助光线在 M1、 M2、 M3、 M4上 的高度;r1、r2、r3、r4和k1、k2、k3、k4分 别 表 示 M1、 M2、 M3、M4的 曲 率 半 径 和 二 次 曲 面 系 数；l1、l2、l3、l4、分别为M1、M2、M3、M4的物距和像距。

三阶单色像差主要包括：球差、慧差、像散、场曲、畸变，分别用SⅠ、SⅡ、SⅢ、SⅣ、SⅤ表示，其公式为[4,20]：

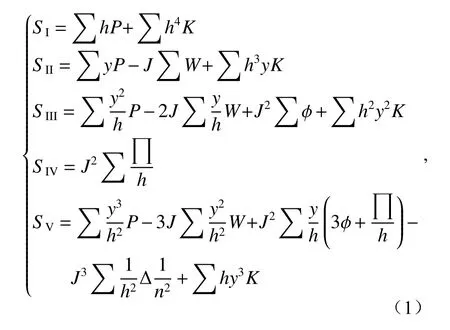
其中，

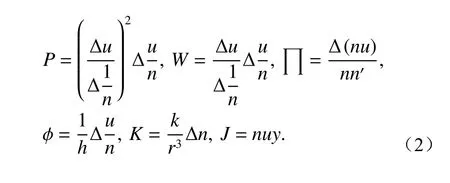
基于近轴近似条件，引入参数：

对于该反射系统，有

对近轴主光线和近轴边缘光线进行光线追迹，得出

Group1中出瞳位置与M4的距离为

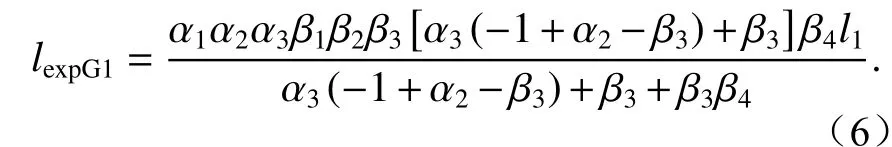
将式（2）～式（4）带入式（1）中即可计算出前镜组G1像差系数。

2.3 像方镜组（Group 2）的像差分析

如图3所示，像方镜组物方视场中心高度为y5， 像方视场中心高度为yim, 物方孔径角为u5，像方远心。光线从中间像点出发，经 M5、 M6到达像点。其中d5、d6分 别表示 M5到M6的镜间距， M6到像面的距离；h5、h6分 别表示第一辅助光线在M5、M6上的高度；r5、r6和k5、k6分 别表示 M5、 M6的曲率半径和二次曲面系数；别 为 M5、M6的物距和像距。

同理，基于近轴近似条件，引入参数：

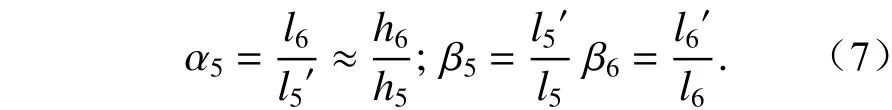
对于该反射系统，有

对近轴主光线和边缘光线进行光线追迹，得出

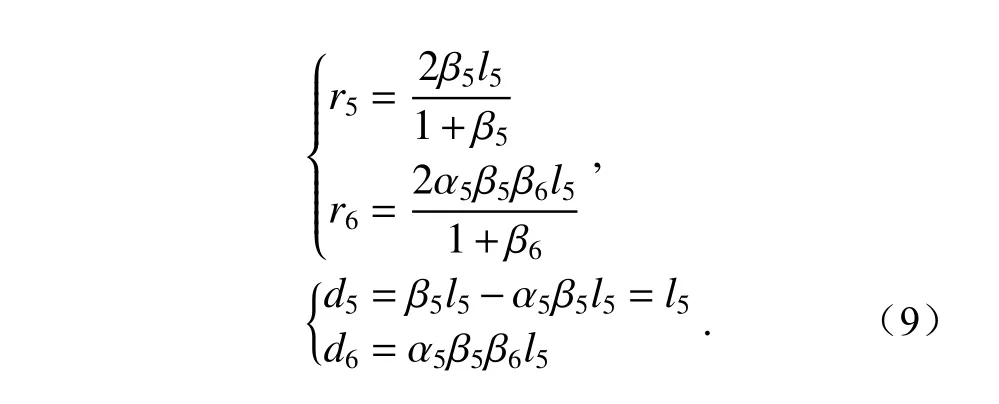
Group2中入瞳位置与M5的距离为

由于光瞳匹配条件，G1的出瞳与G2的入瞳重合，可以算出Group1中入瞳位置与M5的距离为

将式（7）～式（8）带入式（1）中即可计算出后镜组G2像差系数。

2.4 镜组拼接与数学模型建立

对物方镜组与像方镜组进行拼接，拼接原则主要包括物像匹配、倍率匹配以及光瞳匹配。可以得出

共轴光学系统的像差满足线性叠加，即整个光学系统的像差是光学系统中各个元件像差贡献之和。因此离轴六反光学系统的像差系数是Group1与Group 2像差系数之和，利用两个镜组求解的像差系数即可得到光学系统的像差系数。

通过上述像差理论，将极紫外光刻物镜光学系统的三阶像差系数和结构参量参数化。同时，为了满足光学系统的一些特殊要求，引入空间光学追迹方法，将光学系统的特殊要求作为约束将其参数化，在初始结构构建过程中能够有效对遮拦、镜间距、口径、像方远心以及入射角等约束进行控制。基于上述约束条件，由于目标是三阶像差系数尽可能小，因此其评价函数可以写为：

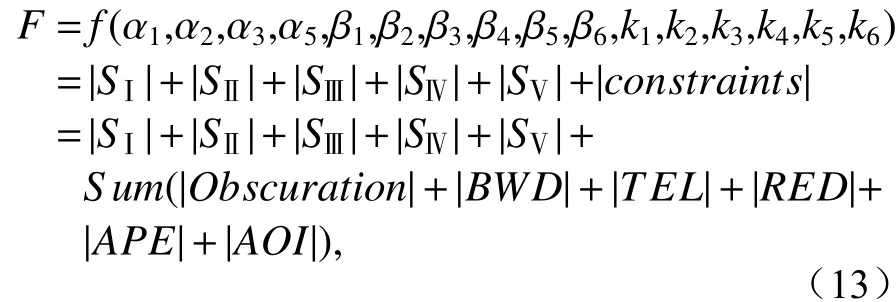
其中constraints表示上述约束。评价函数F反映了光学系统初级像差大小以及约束控制能力，其值越小，则初始结构的初阶像差越小，故该结构的像差控制就越好，实现高成像质量的潜力就越大。本文通过像差理论以及约束控制，建立了极小像差离轴六反参数设计数学模型，将物理模型转化为数学模型，即为高维非线性参数方程求解问题。

3 粒子群算法计算求解离轴六反初始结构数学模型

目前，光学系统结构初始结构计算算法主要是遗传算法[11,21-22]，遗传算法以生物进化为原型，具有良好的全局搜索能力，并因其内在并行性，可以同时进行多个个体的比较，具有可扩展性，易于与其他算法结合。但是遗传算法的局部搜索能力较差，搜索效率低，并且对于初始种群的选择有一定依赖性。粒子群算法（Partical Swarm Optimization，PSO）由Eberhart和Kennedy于1995年提出[23]，该算法的优势在于算法简洁、通用、易于实现、而且计算快速，且不需要梯度信息，是解决非线性优化问题、组合优化问题和混合整数非线性优化问题的有效工具，目前广泛应用于函数优化、神经网络训练、实践工程等应用领域。基础PSO算法也存在一定缺点，在处理高维复杂问题时，算法易于陷入局部值；问题规模较大时，算法收敛速度较慢，精度有限。为了克服基础PSO算法的不足，相关学者提出很多改进方法，主要包括：参数改进与混合算法。参数改进主要通过引入一些新的参数，在改进算法的同时会在一定程度上增加算法的复杂性，包括权重改进的PSO算法、带收缩因子的PSO算法、变学习因子的PSO算法等。混合算法是PSO算法改进的热点方向，在PSO算法中结合其他算法，以提高PSO算法的全局搜索能力和搜索精度，包括基于自然选择的PSO算法、基于杂交的PSO算法、基于模拟退火的PSO算法等[24-25]。

由于学习因子c1和c2决定了粒子本身的经验信息和其他粒子的经验信息对粒子运行轨迹的影响，反映了粒子群之间的信息交流。当c1较大时，会使粒子过多的在局部范围徘徊，当c2较大时，会使粒子过早收敛到局部最小值。为了有效控制粒子的飞行速度以实现全局探测与局部开采两者间的有效平衡，Clerc构造了引入收缩因子的PSO算法，确保PSO算法的收敛性，并可取消对速度的边界限制，能更有效地控制约束粒子的飞行速度，增强算法局部搜索能力。

本文在其基础上，提出了带收缩因子的自然选择的粒子群算法用于离轴六反光学系统初始结构数学模型求解，通过横向对比上述3种混合粒子群算法，并且将模拟退火PSO算法与杂交PSO算法引入收缩因子，同时引入带惯性权重的自然选择PSO算法作为对比。由于收缩因子的引入，其条件为c1+c2>4，Clerc的带收缩因子方法中设c1+c2=4.1，本文图4给出6组不同学习因子下4种算法的收敛曲线，其中1～5组中c1+c2=4.1，第6组c1+c2=4.3，粒子数目N=1000，最大迭代次数为100，退火常数为0.42，杂交概率为0.9，杂交池的大小比例为0.2，惯性权重因子为0.7。表1分别给出了6组学习因子4种算法计算的最小评价函数值，从图4（彩图见期刊电子版）以及表1可以看出，针对以上6组不同学习因子，带收缩因子的自然选择的粒子群算法提升了离轴六反光学系统初始结构数学模型的求解计算精度，对于收敛速度也有很大程度的提升，为离轴六反光学系统设计具备极小像差优化潜力提供设计起点。

带收缩因子的自然选择的粒子群算法的主要流程如图5所示。Step 1：建立离轴六反光学系统初始结构计算数学模型，并随机初始化种群中的粒子位置和速度。Step 2：评价每个粒子的适应度，将当前各粒子的位置和适应度值存于各粒子的个体极值中，计算个体极值和全局最优值，其中个体极值为每个粒子找到的最优解，从这些最优解找到一个全局值，叫做本次全局最优解。Step 3：基于收缩因子，更新每个粒子的速度和位置。Step 4：根据适应度值，更新各粒子间的个体极值与全局最优解。Step 5：将整个粒子群按适应度值排序，用群体中最好的一半的粒子的速度和位置替换最差的一半的位置和速度，保持个体极值和全局最优解不变。Step 6：若满足终止条件（误差足够好或到达最大循环次数）退出，否则返回Step 3。Step 7：根据算法计算结果求解极小像差离轴六反初始结构。

通过带收缩因子的自然选择粒子群算法实现了离轴六反光学系统初始结构求解，其初始结构示意图如图6所示。

4 优化设计

针对以上初始结构进行优化设计，首先在表面面型上对二次曲面面形加入高阶非球面系数以获得高成像质量，同时在优化过程中不破坏初始结构求解中的约束(镜间距、无遮拦、入射角、镜子口径、远心、非球面度等)，使得优化后的结果与初始结构偏差较小，同时在优化过程中控制扰动量(过大会跳过极值，过小会陷入局部极小值)。

基于上述初始结构求解和优化原则，实现了极小像差离轴非球面六反光学系统设计，如图7所示。具体参数指标如表2所示。其总工作距为1371 mm，后工作距为38 mm，像方视场为26 mm×2 mm的弧形视场。元件最大非球面度为60 μm，离轴六反光学系统全视场的最大畸变为1nm，其全视场畸变分布如图8（彩图见期刊电子版）所示。全视场综合波像差为0.011λRMS，其全视场波像差分布如图9（彩图见期刊电子版）所示。根据上述设计结果可知，该设计在实现极小像差的同时满足约束控制，使得极紫外光刻物镜系统更具备工程可实现性。

5 结论

为了解决初始结构构建过程中像差平衡和多约束控制问题，本文基于空间光线追迹与像差矫正相结合的分组设计方法，建立了离轴六反初始结构计算数学模型。提出使用带收缩因子的自然选择的粒子群算法以提高求解精度，提升了设计效率，为离轴六反光学系统设计具备极小像差优化潜力提供设计起点。利用该方法实现了极小像差离轴六反光学系统的设计，其全视场综合波像差为0.011λRMS。

离轴多反光学系统，依然可以利用该方法进行初始结构设计，实现具备像差平衡和多约束控制能力的离轴多反初始结构，为离轴多反光学系统提供具备极小像差优化潜力的设计起点。