环境空气细颗粒物自动监测系统的不确定度评定

文/潘志强 杨硕 高威 周玉龙 王斗文

环境空气细颗粒物自动监测系统 // 因其实时测量的一致性和可靠性、经济性及技术工艺优化和寿命运行周期等优异条件被广泛应用在PM2.5监测上。此评定基于top-down的整体理念，尽可能将所有累加效应纳入到连续和封闭的系统中，在确保可接受水平处于统计受控的前提下，求得质量目标和不确定度的合理估计。

环境空气细颗粒物（PM2.5）是一种时空无法重复的瞬间变异，其实时数据的过程流体抓样分析，存在太多变量和速度太快的组分变化，实验室是无法承担这种检验的。而快捷的自动监测技术具有实时测量的一致性和可靠性，就成本经济、技术工艺优化和寿命运行周期而言，没有任何技术可与之相媲美。

因无法找到PM2.5（μg/m3）合适的参比气体，则分别利用“β射线或振荡天平法（X法）”和“手工称重法（Y法）”作为PTM的经典方法。当测量系统经校准确认无误后，方可对双变量总体进行随机采样分析。

涉及到允差限的采样频率探讨，本文出了X法和Y法两者之间差值（△）下的检出功效（1-β），强调了基于风险与成本权衡的接受概率风险特性操作曲线、两类风险（α和β）下不同样本量（n）、以及错误决策成本可接受水平。

本案例属于非稳定样品分析的研究范畴，涉及到μr,rel(range）和μR'，rel(bat)的两个分量评定。此评定基于top-down的整体理念，尽可能将所有累加效应纳入到连续和封闭的系统中，在确保可接受水平处于统计受控的前提下，求得质量目标和不确定度的合理估计。

由于人们时常要面临危害健康的颗粒物大气雾霾污染风险，因此应建立和完善质量保证（QA）和质量控制（QC）的空气质量监控系统。本文就此对QA和QC的具体程序进行了探讨。

本文参考了bottom-up的做法，在期间精密度和top-down不确定度评定的测量条件下，基于正常的在线系统操作（X法）和手工称重法（Y法），尽量避免由于人为主观的意愿而导致对数据性能的低估，按时对序汇集日常抽取水平下的样品数据集。

基于GB/T 27407-2010实验室质量控制，利用统计质量保证和控制图技术，评价分析测量系统性能的程序，建立X法和Y法两者关系的数据对，利用AD技术来考查由此推导出的残差函数，对其残差系列进行持续监控，以确保数据集质量和发现系统潜在的改进区域、数据对相对变异分析的合理性、以及系统处于受控下top-down不确定度评定的可信性。

在自动监测系统的正常操作下，讨论了允差限的采样频率和相对变异的定量限估计。并在系统质量保证测试，建议给出不确定度评定的两个分量μr,rel(range）和μR’，rel(bat)，维持X法和Y法两者之间的合理性和一致性。

结果

实验数据分析

以某监测站（涵盖子站）所在区域的PM2.5水平监测为例。选择PM2.5最高水平点布局，每隔12天利用X法和Y法，同时段进行独立采样和分析，报出1个具有代表性的数据对（24小时日均结果）。

表1给出该监测站所在地区连续三年汇集的60个代表性数据对，用于PM2.5总体水平和变化趋势的判断和跟踪监测。

表中给出的估计有X=1.001Y-1.315，其决定系数0.99对于X随Y的线性变化趋势解释较强。鉴于系列独立的数据对呈双变量正态分布，不存在预测变量下误差的异方差处理（p=0.84，有0与斜率无差异的方差齐性诊断），可不考虑数据的变换。

图1给出了PM2.5水平下精密度（左图）和偏倚（右图）相对变异的散点图。从中发现，第三年8月份的精密度和偏倚相对变异接近±15%，需要对该年度月份提交的数据对做调查。从总体来看，表1中给出精密度和偏倚的平均结果为5.3%和-2.4%，达到预期的质量目标，且系统残差处于99% 概率下的统计受控，符合实验室内部质量控制活动的初级阶段要求。

表1 成分分析结果

表1 X法和Y法的PM2.5数据对统计汇总

图1 精密度和偏倚相对变异的散点图

允差限的采样频率探讨

图2给出了X法和Y法两者之间差值（△）下的检出功效（1-β）作图，这是一种基于风险与成本权衡的接受概率风险特性操作曲线。本案例根据不同样本量（n），探讨了两类风险（α和β）与错误决策成本可接受水平下的采样频率。图2中n的表述有：

图2 对应n下的检出功效风险曲线图

n=60（每年取样量不得少于22个数据对，相当于每12天抽取1个数据对）；

n=100（每年取样量不得少于44个数据对，相当于每6天抽取1个数据对）；

n=200（每年取样量不得少于66个数据对，相当于每3天抽取1个数据对）。

尽管表中的采样频率（n=60）节省资源，且在90% 双侧区间下所求得的△值（1.70~0.74）处于最大允限±2范围内（相当于X=1.001Y-1.315的截距0检验），但图2显示，其检出功效的失败风险却大于10%（n=100和n=200的风险小于10%）。

故在可容许最大偏倚△值和成本权衡下，建议每6天1次的采样频率为宜，此采样频率也有助于降低质量目标的上限。

相对变异的定量限估计

水平过低的相对变异会趋大。由此，本文针对表中的水平区间与其相对变异，进行了两者关系的定量限估计，这种估计思路与美国EPA非常接近，见图3。

由图3可知，高水平的变异趋于一致（≤15%），EPA水平的15（μg/m3）变异大于20（μg/m3），但两者的上限差异不大。本案例假设定量限为10%（标准差/水平=1），则根据表中的升序水平及其对应的相对变异，经幂函数的统计拟合求得的定量限有： 17.851.08=23≈20μg/m3）。

图3 本案例与EPA数据非线性回归的定量限比较

本案例建议，该监测站所在区域的PM2.5监测，可以不考虑20（μg/m3）以下的数据纳入，以避免过于接近系统阈值而失去对偏倚的监控。

不确定度分量评定

鉴于上述分析的合理性，则可采用表中给出的Rerl=5.3%求得：μr,rel(range）=4.7%。

测量系统独立确认的偏倚检查有：内外气密性、零点跨度、滤膜、流量、温度和压力校准等，这些都与PM2.5的性能监控直接相关联，然而，本案例关注更多的是采样器正确流速下的流量调试变异，即另个分量μR'，rel(bat)。

PM2.5的判别来自内部流速控制系统的进口管和分割器，因其变化直接影响到PM2.5实际体积流速的变化，则要求恒定在所设定的两个指标上：一个是皂膜流量与16.67（L/min）的变异≤±5%；另一个是采样器与皂膜流量间的变异≤±4%。本案例利用每月质量检验后的皂膜流量计，来对现场采样器进行如下的流量传递和校准：

解锁仪器键盘进入流量校准模式，摘掉采样顶端颗粒物切割器并接入流量计。流量计读数稳定后记录测量值。在校准模式中输入平均值予以保存，退出后进入正常测量模式，取下流量计装回颗粒物切割器，校准结束。

鉴于表中的流量调试符合要求，则无需实施进一步的多点校准确认。流量调试数据结果需接受系列残差的正态分布假设（见图4），该系列残差的假设来自于双变量随机分布的回归分析（X=1.015Y-0.357）。图4中的分析结论如下：

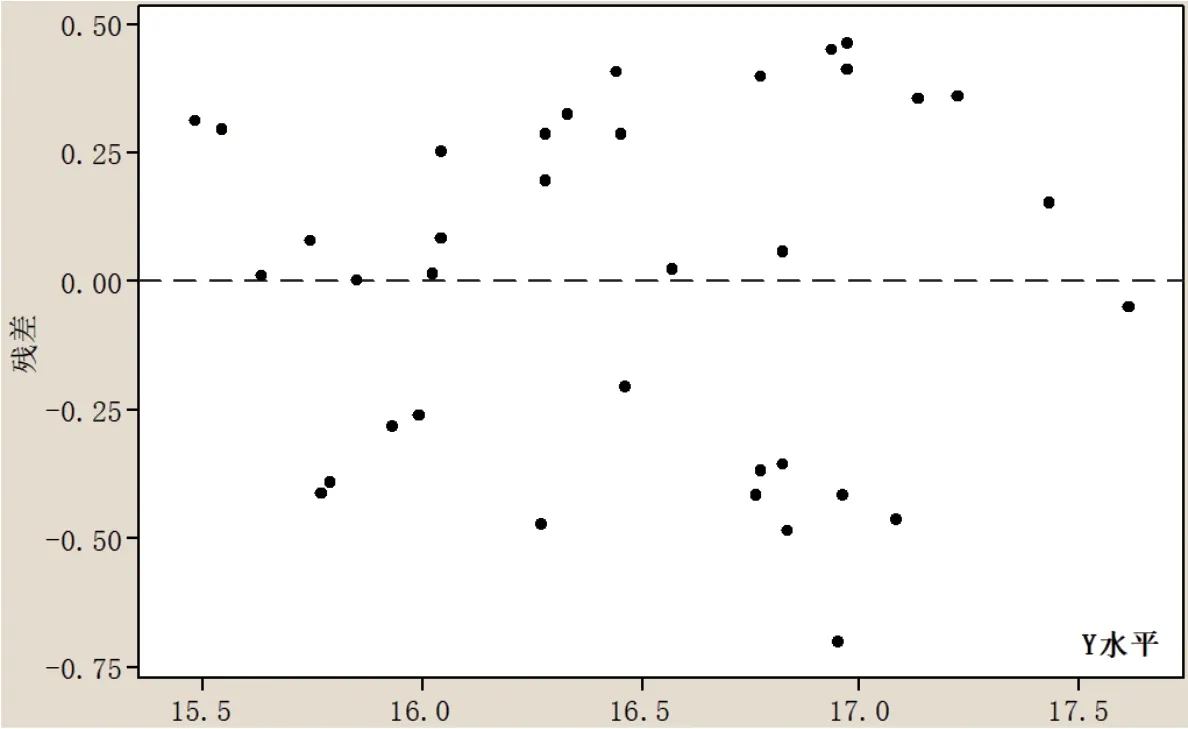
图4 Y法水平下的残差分布图

残差和趋于0；残差不存在极值；随Y法水平的递增，残差作图未见曲率形态，也未见纵向散点分布；接受99% 概率下的AD统计原假设。

上述的判定结论支持了X=1.015Y-0.357常数模型的选择（但不考虑利用回归分析对采样器流速的传感器做调整）。

综上所述和表2的统计，监测站认为，不确定度分量μr,rel(range）=4.7%。，可以忽略校准不确定度和 μR'，rel(bat)的贡献。

表2 成分分析结果

表2 瞬时流量校准（工况）的代表性测量数据

因μr,rel(range和μR'，rel(bat)被忽略，则可直接求得：Urel=2μr,rel(range）=9.4%。

结论

本案例有如下建议：

每6天1个数据对的三年积累，有助于优化质量目标和不确定度的估计。

相对变异（≤10%）和定量限的研究，有助于避免过分变异对质量目标和不确定度的影。

Urel==9.4%估计并非一成不变，需经长期持续的跟踪监测，有助于做出正确的质量目标决策。

立足top-down总体理念，对各种资源的变动趋势进行统一监控，有助于不同现场和多设备的远程诊断保持在可接受的决策误差水平上。