卡尔曼滤波框架下基于最大相关熵的移动机器人位姿估计
李志鹏,程 兰,王志飞,阎高伟
(太原理工大学 电气与动力工程学院,太原 030024)
同时定位和建图(simultaneous localization and mapping,SLAM)是机器人实现环境感知、确定自身位置的关键技术[1-3]。而机器人的位姿估计精度直接决定机器人的定位精度,进而影响建图精度。因此,提高位姿估计的精度一直是机器人领域研究者不断追求的目标。
基于卡尔曼滤波的状态估计算法是实现机器人位姿估计最常用的技术手段。文献[4]实现了基于扩展卡尔曼滤波(extended kalman filter,EKF)的移动机器人位姿估计算法,仿真结果表明EKF有良好的估计性能。文献[5]提出了迭代扩展卡尔曼滤波(iterated extended kalman filter,IEKF),利用最新的估计结果对非线性测量函数进行线性化迭代,有效地提高了EKF的位姿估计精度。此外,文献[6]利用麦夸尔特法推导了新的滤波器LMEKF,利用迭代更新的方式改进了EKF的更新步骤,进一步提高了IEKF的位姿估计精度。但以上滤波方法都要求非线性函数可微,进行线性化时往往会产生一定的偏差,且需要计算雅可比矩阵。
为了避免线性化带来的位姿估计偏差,研究者将UKF用于位姿估计,通过对一些Sigma点的无迹变换来估计位姿,得到了基于UKF的位姿估计算法[7]。然而,基于EKF和UKF的位姿估计算法都假设状态噪声和测量噪声服从高斯分布,并不适用于非高斯噪声。然而在机器人定位与建图过程中,非高斯噪声确是客观存在的,如移动汽车的噪声、由于电磁干扰以及通信系统故障和缺陷而导致的脉冲噪声等。
针对EKF和UKF的局限性,研究者提出了适用于非高斯噪声的位姿估计算法,如基于粒子滤波(particle filter,PF)[8]的位姿估计算法、基于高斯和滤波(gaussian sum filter,GSF)[9]的位姿估计算法等。这些算法利用大量的样本来逼近位姿的后验概率密度函数,虽然在估计精度上得到了改善,但存在计算量大的问题。
近年来,研究者开始将相关熵用于处理非高斯噪声下的位姿估计问题[10-11]。相关熵是对两个随机变量之间相似性的一种度量。文献[12]介绍了最大相关熵(maximum correntropy,MC)在非高斯噪声环境中的应用,基于MC的位姿估计算法能够明显提高位姿估计精度。之后又有学者将MC应用于卡尔曼滤波理论中,如相关卡尔曼滤波器(C-KF)[13]、最大相关熵卡尔曼滤波器(MCKF)[14-15]、最大相关熵扩展卡尔曼滤波器(MCEKF)[16-18]以及最大相关熵无迹卡尔曼滤波器(MCUKF)[19]等。MC在基于卡尔曼滤波器中的应用证明了将MC和基于卡尔曼滤波算法相结合实现非高斯噪声下的位姿估计的可行性。但现有的基于MC和卡尔曼滤波算法的移动机器人位姿估计算法只利用了位姿估计结果的先验信息,没有充分利用最新的位姿估计结果去更新预测的测量结果。
本文针对上述问题,提出了在UKF框架下基于MC的移动机器人位姿估计算法。利用MC在处理非高斯噪声中的优势,代替最小方差标准来构造新的代价函数,通过麦夸尔特法对该函数的优化实现在UKF框架下移动机器人的位姿估计。
1 问题描述
所采用的移动机器人模型如图1所示[20]。该模型可以表示二维平面上的自主移动机器人的一般运动模型。机器人的状态根据运动学模型定义为表示机器人的位置坐标,表示转向角,控制输入量为舵角和速度。
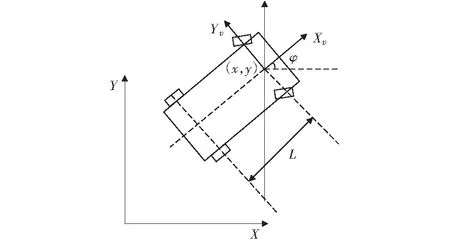
图1 移动机器人模型Fig.1 Model of mobile robot
1.1 移动机器人运动模型
为研究方便,可将图1中的移动机器人模型转换为一长为L的连杆,前端两侧车轮的速度为v,如图2所示。
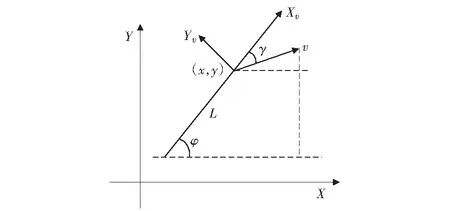
图2 移动机器人简化模型Fig.2 Simplified model of mobile robot
根据图2,对移动机器人的运动学模型进行建模,可得机器人运动方程:
(1)
转化为矩阵形式:
(2)
式中:ω(i)表示状态噪声。
1.2 移动机器人观测模型
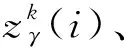
(3)
式中:(xk,yk)表示路标点的位置坐标,rk(i)表示观测噪声。
综上,式(2)和(3)构成系统的状态方程和观测方程。本文通过对状态向量xv的估计来实现对移动机器人位姿的估计。
2 相关工作
本文算法是在MCUKF[19]的基础上进行改进的,为了说明本文算法与MCUKF的不同,首先对相关熵和MCUKF进行简要介绍。
2.1 相关熵理论
由于MCUKF引入了相关熵,为确保内容的完整性,本节首先对相关熵进行介绍。相关熵是一种相似性度量方法,给定两个随机变量X和Y,则其相关熵为[13]:
(4)
式中:E[·]为期望算子,FX,Y(x,y)为X,Y的联合分布,φ(x,y)表示Mercer核函数,如常用的高斯核函数Gδ(e)=exp(-e2/2δ2),这里e=x-y.实际中很难直接计算相关熵,因此通常采用数据驱动的方式对其进行估计。即假设采集到的关于x和y的样本为{x(i),y(i)},i=1,2,…,n,则X,Y的相关熵可通过下式进行估计:
(5)
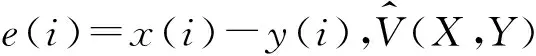
(6)
高斯相关熵包含了所有由核带宽δ加权的X和Y的偶矩。选择合适的δ,将高阶矩纳入到信号处理算法中,可以更加准确地描述非高斯分布的高阶特性,这是相关熵处理非高斯噪声的主要优点。
2.2 MCUKF算法
MCUKF考虑的状态空间模型为:
(7)
式中:xi和zi分别为第i时刻的系统状态和测量值,非线性函数fi(g)和hi(g)已知,过程噪声ωi和测量噪声vi不相关,其均值为零,协方差为Qi和Ri.初始状态x0的均值和协方差P0为0.在MCUKF中,假设过程噪声ωi服从高斯分布,而测量噪声vi服从非高斯分布。
MCUKF的预测步骤与传统UKF相同:
(8)
(9)
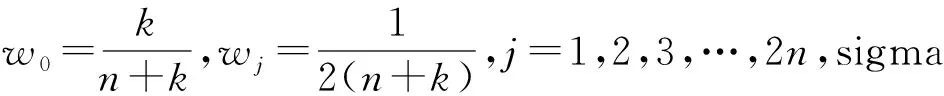
(10)
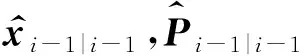
对于滤波更新步骤,MCUKF利用最小方差标准来处理高斯过程噪声,利用MC来处理非高斯测量噪声,其所采用的代价函数为[19]:
(11)
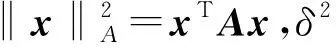
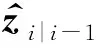
(12)
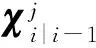
(13)
测量矩阵Hi表示为:
(14)
式中:
(15)
则更新的测量噪声矩阵Ri表示为:
(16)
式中,
(17)
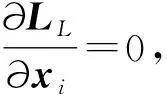
(18)
式中,
(19)
(20)
协方差估计结果为:
(21)
MCUKF引入权重Li来调优增益Ki,以避免非高斯噪声对测量值的干扰。但MCUKF只考虑了过程噪声ωi为高斯分布的情况,且在滤波步中只是根据状态的预测结果来更新预测的测量值,导致最终的估计结果精度不高。针对此问题,本文借鉴IEKF中迭代估计的思路,提出了迭代的MCUKF,即MCIUKF,并利用麦夸尔特法推导了滤波更新方程。
3 位姿估计算法(MCIUKF)
基于上一节的描述,MCUKF存在的问题有:1) 过程噪声没有考虑非高斯分布的情况,且没有充分利用最新的估计结果;2) 文献[19]对MCUKF的研究只进行了数值仿真,并没有用于解决实际问题。
针对这些问题,本文提出MCIUKF算法,利用MC来处理非高斯过程噪声和非高斯测量噪声,用MC代替最小方差标准设计新的代价函数,并在测量矩阵中纳入最新的位姿估计结果,以提高在非高斯噪声环境下的估计性能。最后将该算法应用于移动机器人的位姿估计。
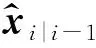
(22)
然后通过求解以下优化问题进行滤波更新:
(23)
由于上述优化很难得到解析解,考虑一种基于梯度的迭代方法来求解式(23),即麦夸尔特法。在迭代滤波算法中,高斯牛顿法被广泛应用于解决非线性优化问题,而麦夸尔特法可以进一步提高高斯牛顿法的收敛性,获得更好的滤波性能[5-6]。
利用麦夸尔特法迭代求解如下:
(24)
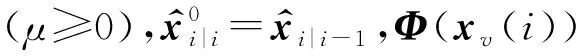
(25)
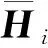
(26)
(27)
(28)
式中,
(29)
(30)
Φ(xv(i))表示为:
(31)
将式(25)和式(31)代入式(24)可得状态估计:
(32)
式中,
(33)
(34)
(35)
(36)
协方差估计为:
(37)
4 算法实现
本文当前研究假设机器人总是可以观测到足够数量的路标点以实现位姿估计。本节将所提出的算法用于移动机器人的位姿估计,而实现机器人位姿估计的前提是数据关联。下面将主要介绍数据关联、状态向量增广及算法的伪代码,为位姿估计算法的实现做准备。
4.1 数据关联
在SLAM的滤波更新阶段,需要对观测到的路标和状态向量中的路标进行匹配,这一过程被称为数据关联。在路标数目不多、存储资源富裕的情况下,可以直接维护一个表达所有路标在状态向量中位置的列表,table[id]代表编号为id的路标在状态向量中的位置,table[id] = 0代表该路标未在状态向量中出现。当机器人观测到新路标时,需要将新路标添加到待估向量中,即需要进行状态向量增广。
4.2 状态向量增广
状态向量增广是将新观测到的路标信息添加到状态向量及协方差矩阵中,同时改变状态向量及协方差矩阵的维度。若一个新观测到的路标点为z,其对应的全局坐标为m=(mx,my)T,此时机器人位姿为xv=[x,y,φ]T,则根据观测模型可得z到m的转换为:
(38)
将m添加到状态向量中:
(39)
4.3 程序伪代码
本文整体的算法流程如下。

其中,步骤3,4表示滤波预测过程,步骤5表示数据关联,步骤7-16表示滤波更新过程,步骤18表示状态向量增广。
5 仿真分析
5.1 仿真环境设置
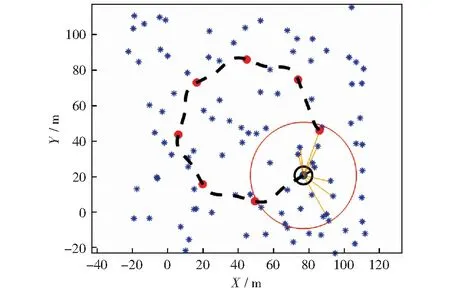
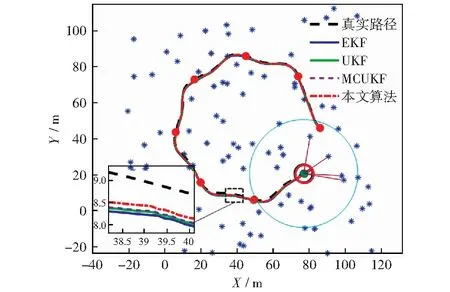
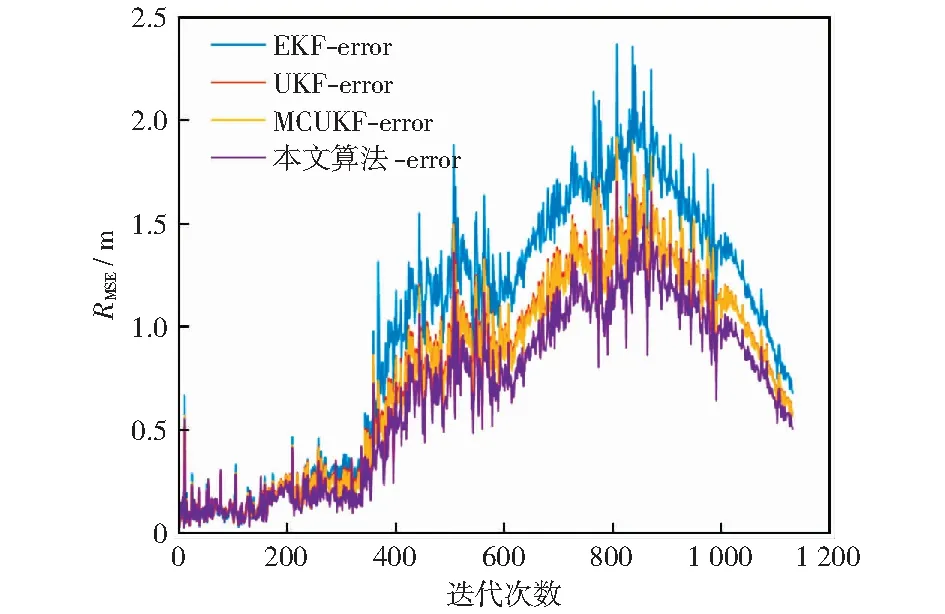
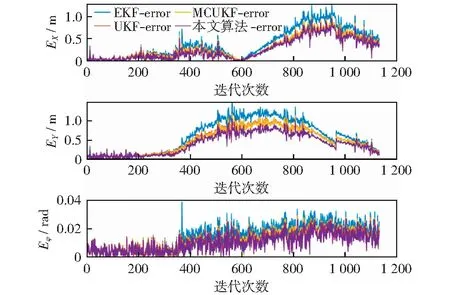
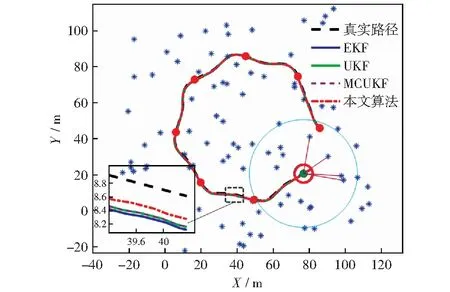
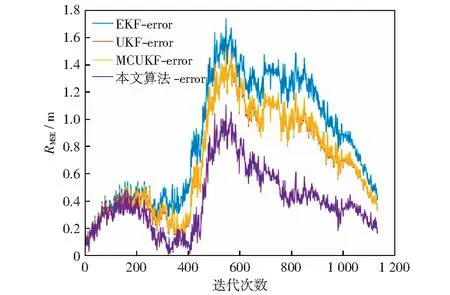
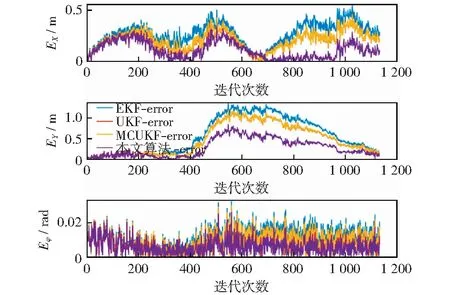
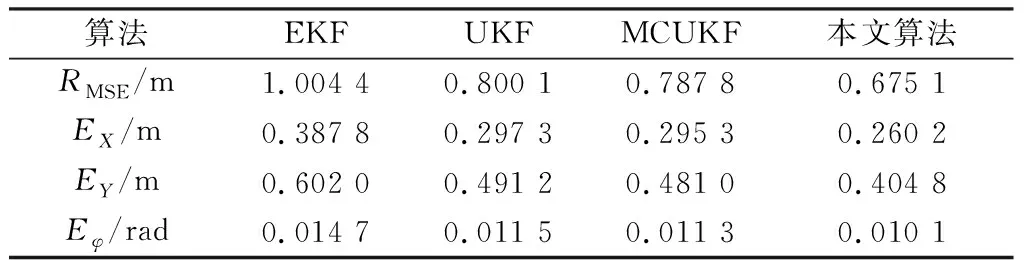
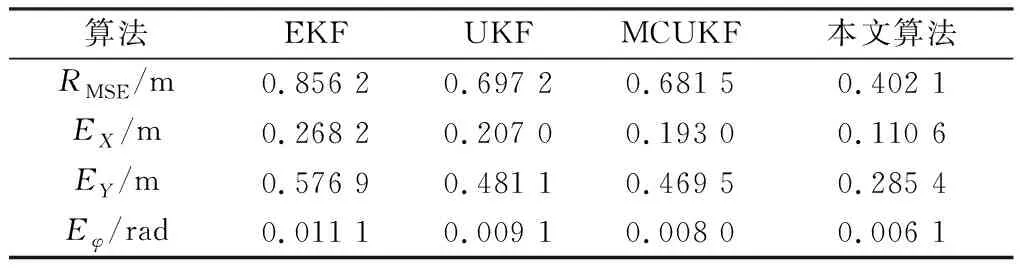
为了分析算法的性能,用Matlab模拟了移动机器人采用激光雷达观测数据并进行位姿估计的仿真环境。机器人的的仿真参数设置为:轮距L=4 m,速度vvad=8 m/s,最大舵角xmax=30°,最大转向速度θ=20°/s,最大观测距离d=30 m,控制周期为0.025 s,调整权重δ=8,阻尼参数μ=0.001.为更接近真实的应用场景,令传感器的观测范围仅为车前半径为d的半圆内的路标点,并对速度、最大舵角及转向速度进行限制,即v=vrat,|γ| 所考虑的非高斯噪声分别为脉冲噪声和有色噪声,本节针对这两种噪声分析所提出算法的性能。利用混合高斯噪声分布来表示脉冲噪声,其分布函数为: (40) 考虑的有色噪声分布函数为[21]: fc(k)=fw(k)+c1gfw(k-1)-c2gfw(k-2) . (41) 移动机器人运行的实际轨迹和所观测的路标点如图3所示。其中蓝色星号代表路标点,红色圆点代表路径上的关键点,外围有蓝色圆圈的为机器人的下一目标点,黑色虚线代表机器人的真实轨迹,黑色圆代表机器人,蓝色圆点为当前机器人位置,蓝色圆点与黑色圆边上点的连线代表机器人目前航向,有与蓝色点连线的路标代表其被机器人传感器观测到,红色圆圈代表传感器的观测半径,传感器仅观测机器人正前方180°范围内的路标点。 图3 机器人运行轨迹Fig.3 Robot trajectory 5.2.1误差与稳定性分析 本文采用蒙特卡罗仿真,连续运行50次程序,并利用均方根误差(RMSE)来衡量算法的性能。同时将仿真结果与EKF[4],UKF[7],MCUKF[19]进行了对比分析。 第i次迭代的均方根误差表示为: (42) 第i次迭代的状态估计误差表示为: (43) (44) (45) 图4 脉冲噪声下4种算法的估计轨迹Fig.4 Estimated trajectories of four algorithms under impulse noise 图5 脉冲噪声下4种算法位姿估计结果的均方根误差Fig.5 RMSEs of pose estimation results of four algorithms under impulse noise 图6 脉冲噪声下4种算法的状态估计误差Fig.6 State estimation errors of four algorithms under impulse noise 图7 有色噪声下4种算法的估计轨迹Fig.7 Estimated trajectories of four algorithms under colored noise 在不同噪声环境下各算法的平均误差对比结果如表1、表2所示。 由图4-图6以及表1可以直观地看出,在脉冲噪声环境下,本文算法在精度上明显优于其它算法,并且与MCUKF相比,本文算法的均方根误差平均降低了0.112 7 m;由图7-图9以及表2可以看出,在有色噪声环境下,本文算法相对于其它算法有更好的位姿估计精度,并且与MCUKF相比,本文算法的均方根误差平均降低了0.279 4 m.同时本文算法具有较好的数值稳定性,这主要是由于采用了基于MC的代价函数,并在测量矩阵中纳入了最新估计,提高了位姿估计精度。而EKF,UKF只是在高斯噪声下有较好的估计性能;MCUKF则是由于更新过程中测量矩阵利用的是先验估计信息,导致其估计精度降低。仿真结果证明了将MCIUKF用于机器人位姿估计的有效性。 图8 有色噪声下4种算法位姿估计结果的均方根误差Fig.8 RMSEs of pose estimation results of four algorithms under colored noise 图9 有色噪声下4种算法的状态估计误差Fig.9 State estimation errors of four algorithms under colored noise 表1 脉冲噪声下4种算法的平均误差对比Table 1 Average error comparison of four algorithms under impulse noise 表2 有色噪声下4种算法的平均误差对比Table 2 Average error comparison of four algorithms under colored noise 5.2.2时间复杂度分析 本文使用的计算机系统型号为戴尔Inspiron 3576,运行内存为8 G,显示内存为128 MB,各算法单次迭代时间复杂度对比如表3所示。 表3 时间复杂度对比Table 3 Time complexity comparison 由表3可知,本文算法在时间复杂度方面稍逊于其它算法,这是由于算法引入了最大相关熵,对熵的计算导致了计算复杂度的增加;另外,在算法的更新环节利用麦夸尔特法进行迭代求解也增加了时间复杂度,进而使算法的实时性相对较低。 本文提出了一种适用于非高斯噪声环境的基于MC和IUKF相结合的位姿估计算法,提高了算法在非高斯噪声下的位姿估计精度。本文的主要贡献:1) 在滤波更新步骤定义了一个基于MC的代价函数,并利用麦夸尔特法推导出对应的滤波更新方程,得到了MCIUKF滤波器;2) 将所提出的MCIUKF算法应用于移动机器人的位姿估计。在非高斯噪声环境下,与对比算法相比,本文算法能够明显提高位姿估计的精度。但所提出的算法由于采用了最大相关熵,导致其实时性相对较低,这也是未来工作的研究方向。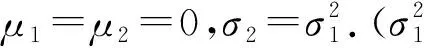
5.2 仿真结果分析
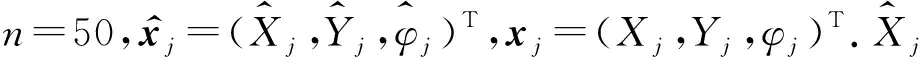

6 结束语

