日间对流边界层中的非局地动量混合

赵昭 周博闻

(1 中尺度灾害性天气教育部重点实验室，南京 210023；2 南京大学 大气科学学院，南京 210023)

引 言

图1 组织化上升流和局地湍流概念图(左侧)以及对流边界层中的典型位温、感热通量、纬向风和动量通量廓线(右侧)Fig.1 Schematic of the organized updrafts and local eddies(left), and classic vertical profiles of potential temperature, heat flux, streamwise velocity and momentum flux in the convective boundary layer(right)

湍流是一种复杂的多时空尺度运动[1]，也是大气边界层的主要特征[2]。白天，在地面加热的作用下，大气边界层湍流由边界层热力次级环流主导。因此，日间边界层也被称为对流边界层(Convective Boundary Layer, CBL)。不同于湍流的紊乱和瞬变，边界层热力环流在空间上呈现出规则的组织化特征，在时间上则具有相比湍流特征时间尺度更稳定的生命周期[3]。边界层对流的组织形态受地表加热和水平风速的垂直切变共同作用：在热力主导下呈现水平辐条状单体特征[3-4]，在切变主导下则转变为风切方向延伸的准二维滚涡[5-6]。如图1所示，边界层对流由近地层的热羽辐合组织而成，在混合层中向上旺盛发展直至混合层顶，而后进入层结稳定的夹卷层中，在负浮力的作用下减速并水平辐散[7]，从而形成广域的下沉回路[8]。基于上述垂直相干结构，组织化对流也被称为非局地热对流，是对流边界层中最具能量的湍流运动，其特征垂直距离与水平距离尺度皆与边界层厚度相仿。同时，大气边界层充斥着无处不在的、相对于边界层厚度而言尺度较小的湍涡。这类湍涡或由风切变或热力作用生成，或在湍流串级过程中由更大尺度湍涡破碎形成，呈现经典的惯性子区湍流特征。相对非局地组织化对流，尺度更小的湍流也被称为局地湍涡。

组织化对流对大气边界层内热量、动量、水汽及其他标量的垂直输送一直是对流边界层的研究重点和热点[9]。关于组织化对流对热量的垂直输送，前人从观测事实到物理机制都已形成较为全面系统的认识[10-18]。组织化对流是边界层热量垂直输送的主要过程：旺盛的非局地对流能将地面的热量向上输送至混合层，而部分含能热泡在突破混合层顶进入夹卷层后，还能夹带高位温的自由大气返回边界层，从而实现自上而下的边界层加热。在地面与自由大气的双重加热作用下，对流边界层的位温多呈现图1所示的底层超绝热，上层静力稳定的垂直分布[19-20]，而感热通量在对流边界层内则呈线性分布，代表了以组织化对流为主的湍流对边界层各个高度的均匀加热(即常值垂直感热通量散度)。组织化对流从地面到混合层上半部分的非局地传输，造成弱稳定层结环境下的向上热量输送(图1)，即由组织化对流所主导的非局地感热通量，在混合层上层与位温垂直梯度的符号一致，这一现象也被称为逆梯度输送[21-22]。

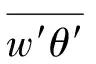
(1)

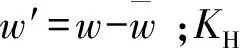
(2)

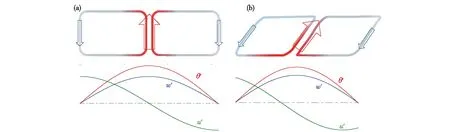
图2 (a)理想热力自由对流(瑞利—贝纳德对流)及相应θ′、w′和u′的相位示意图和(b)切变热对流及相应相位示意图Fig.2 Schematic of the free convective circulations of the Rayleigh-Bénard type (a), and sheared convective circulations (b)(The relative phase of θ′, w′ and u′ are sketched at the bottom)

其中：γ的符号为正，且仅在对流边界层内给予赋值。这一参数化方法经过Troen, et al[25]和Holtslag, et al[27]等研究者的发展，目前已被许多边界层方案采用，其中就包括应用较广的YSU方案[34]、BOULAC方案[35]等。但近年来，ZHOU, et al[18]指出γ所代表的物理机制存在缺陷，即公式(2)中的逆梯度修正通量KHγ，与其所代表的组织化对流所造成的非局地湍流之间，存在概念偏差，这一缺陷也被Chor, et al[36]等证实。

在目前对动量通量的参数化方法中，由于组织化湍流对动量输送的贡献并不明确，且风廓线与位温廓线不同，在大多数情况下，边界层风速受地面摩擦作用，随高度单调递增，风切变的符号在边界层内一致，并与动量通量的符号相反(如图1)，满足梯度扩散假设。因此，在常用的边界层方案中，除YSU等少数方案以外，多数边界层方案仅采用K-理论参数化动量通量，且并不考虑非局地通量，如MYJ方案[44-45]、MYNN方案[46-47]、BOULAC方案[35]等。但出于物理过程完整性的考虑，Frech, et al[48]提出了一种动量通量的非局地修正方案，Brown, et al[49]利用大涡模拟资料评估了该方案在不同稳定度和在正压、斜压条件下的表现，发现非局地项的加入提升了方案的模拟效果。经Noh, et al[26]的进一步发展后，参数化的非局地动量通量被YSU边界层方案所采用[34]。

本文针对对流边界层中的动量混合开展研究，旨在探究组织化对流对动量输送的贡献。文中所考虑的是相对简单的正压条件下的对流边界层，即气压梯度力(地转风)的大小和方向皆不随高度变化。在实际情况中，多存在斜压情况，即地转风向量(ug,vg)的方向和大小都随高度变化。在斜压条件下的动量输送更为复杂，地转风的切变也会影响边界层的风切变[50,51]。总体而言，相比正压条件，斜压对流边界层的研究较少。本文仅研究正压条件下的动量通量输送，对斜压边界层的动量输送则将在后续的研究中展开。本文以高时空分辨率的大涡模拟(Large Eddy Simulation, LES)结果为基本研究资料，开展不同稳定度下的对流边界层模拟，以便讨论不同形态的有组织对流对动量输送的影响。为研究组织化对流，首先必须将其从背景湍流中剥离，但目前尚未有客观准确的分离方法[18]。因此，本文选取3种滤波方法对组织化对流进行分离，包括经典的傅里叶变换滤波，以及本征正交分解和经验模态分解两种先进方法，目的是通过基于不同原理的方法，从而获得定性一致的结果。而后，基于分离所得组织化对流，开展动量通量的系统性研究，包括非局地与局地通量的量化、通量输送效率以及协谱分析等，深刻认识组织化对流对动量输送的贡献。

1 大涡模拟的实验设置与模式资料

通过控制不同的地表加热和地转风速，参照Shin, et al[16]的实验设置，对4个理想对流边界层个例进行了大涡模拟实验，表1展示了相应的配置参数。4个个例相应的整体稳定度参数由ζ=-zi/Lo表示，其中zi为边界层厚度，Lo为奥布霍夫尺度，ζ的取值范围从正无穷大到零，分别对应了自由对流和中性层结环境[52]。从B5到S15，浮力作用逐渐减弱，切变作用增强，ζ随之变小，对流组织形态亦从单体(ζ≥20)过渡到滚涡(ζ≤20)。模式初始场与Shin, et al[16]一致，初始风廓线均设为地转风速，初始位温设置为等熵廓线，并在1 km高度设置覆盖逆温层，以限制边界层的增长。

模拟采用了由俄克拉荷马大学风暴分析预测中心开发的进阶区域预报模(Advanced Regional Prediction System, ARPS)模式，该模式为非静力中尺度与对流尺度有限差分模式，也适用于大涡模拟[53-54]。模拟区域为10.08 km×10.08 km×2.0 km，水平分辨率为10 m，垂直分辨率在1.3 km高度以下为4 m，以上逐渐拉升至50 m。在此高分辨率下，除了贴地2～3个垂直层外，次网格尺度的影响基本可以忽略。模式水平方向采用双周期边界条件，垂直方向采用半滑动边界条件，顶部500 m采用瑞利阻尼。模式的次网格湍流采用Moeng[55]的1.5阶湍动能闭合方案。模式积分至准定常态，B5和B10个例需2 h，S10个例需5 h，S15个例6 h。而后，继续积分2 h以获得分析数据，数据每10 min输出一次。

表1 模型个例参数Table 1 List of model parameters for all cases

2 流场分离

本节简要介绍3种组织化对流的分离方法，即傅里叶变换、本征正交分解和经验模态分解，以垂直扰动速度w′为例进行分离，并展示分解后的流场，其他方向扰动速度场类似，因此不再展示。

2.1 傅里叶变换

傅里叶变换(Fourier Transform, FT)将物理空间变量投影至谱空间，从而将物理空间的扰动分解为不同波数或频率的扰动。基于傅里叶变换的滤波被广泛应用于湍流的谱分析。本文对各高度层扰动场做二维傅里叶变换，以z高度的垂直扰动速度w′为例：

(3)

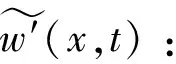
(4)

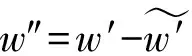
2.2 本征正交分解

本征正交分解(Proper Orthogonal Decomposition, POD)是一种基于数据的降维分析方法[56]。它通过提取正交模态，对数据进行最优近似重构，从而得到原数据的降维表达。其分解的模态则依据能量由高到低排列，前几个模态往往包含了绝大多数的扰动能量[57]。本研究采用Sirovich[58]为高维数据和大型矩阵所设计的“快照”法进行POD分解。以w′为例，将某一时刻的三维扰动场w′(nx×ny×nz)重构成维度为nxy×nz的二维场(nxy=nx×ny),以短维nz构建协方差矩阵C(nz×nz)：

(5)

通过上式解得C的nz个特征值，降序排列为λi(i=1…nz)，其相对应的特征向量为si(i=1…nz)。为了得到完整的三维场，将si投影到原场w′(nxy×nz)中并做单位化处理，得到矩阵R(nxy×nz)：

(6)

接下来通过R计算POD系数矩阵P(nz×nz)：

P=RTw′，

(7)

P的nz列包含了每个水平LES网格层的nz个POD模态的系数。根据R矩阵的性质，可以通过w′=RP重现原场，主观地取前mc个模态，作为有组织对流的部分，

(8)

从而完成POD方法对组织化结构的提取。

2.3 经验模态分解

经验模态分解(Empirical Mode Decomposition, EMD)最初是一种针对时频域所发展的分解方法[59]，尤其适合非线性和非稳定的信号。EMD克服了基函数无自适应性的问题，对复杂的非稳定信号逐级进行平稳化处理，从而将不同周期的波动分解成有限个本征模态函数(Intrinsic Mode Function, IMF)。采用Bhuiyan, et al[60]的方法，将EMD方法运用到二维空间序列中，以每一高度层的速度扰动场作为分解对象，将组成该扰动信号的各尺度分量从高波数到低波数进行提取，具体算法上采用Thirumalaisamy, et al[61]所发展的“快速自适应经验模态分解”(Fast and Adaptive Empirical Mode Decomposition, FA-EMD)算法，以w′为例，则有：

w′=∑wIMF+residual，

(9)

w′分解为有限个wIMF与残余项(residual)之和，则代表局地湍流部分的扰动场为：

(10)

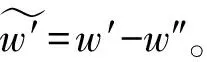
2.4 分离效果

图3展示了B5和S10个例在200 m高度上的w′水平剖面。在图3a中，由辐条状快速上升气流和及广域下沉气流所组成的多边形单体结构清晰可见。而在图3b中，w′在加热减弱，风切增强的条件下，呈现出沿风切方向的条状上升气流，对应准二维边界层滚涡结构。

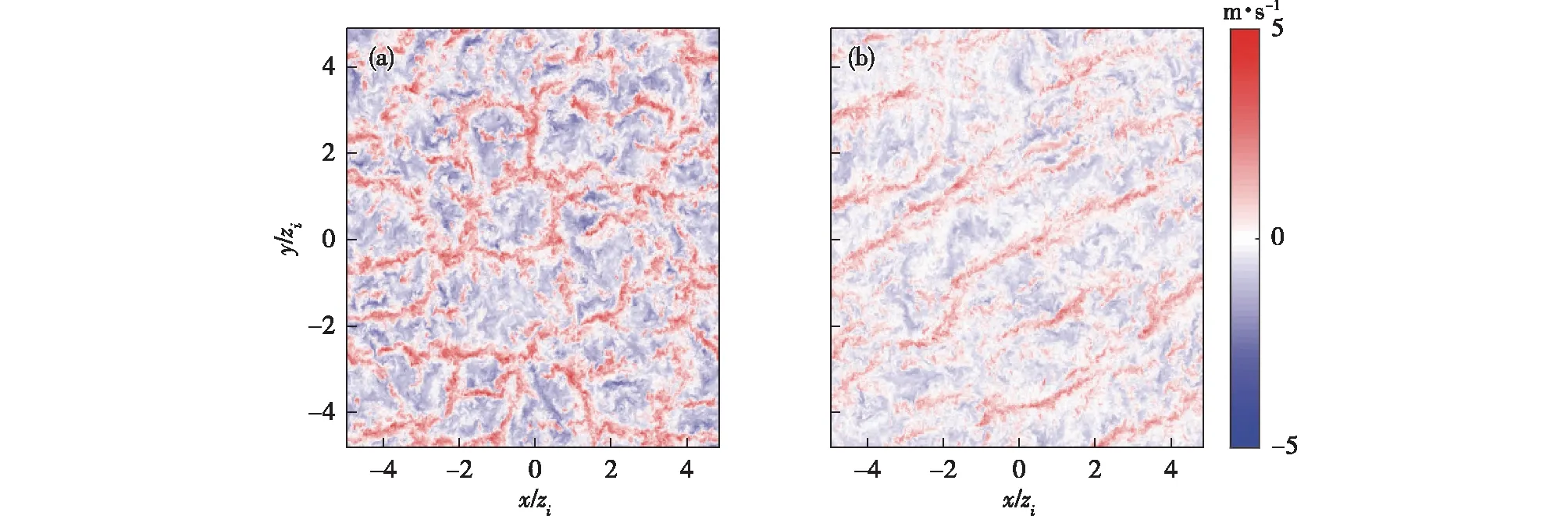
图3 B5和S10个例在200 m高度上的w′水平剖面(单位：m·s-1): (a)B5个例积分4 h; (b)S10个例积分7 hFig.3 Visualization of w′ at 200 m for case B5 and S10 (unit:m·s-1): (a) case B5 integrated for 4 h; (b) S10 integrated for 7 h

图4 B5个例积分4 h的流场在200 m高度通过3种方法滤波所得的组织化对流的水平剖面(单位：m·s-1)(其中FT选取截断波数kc=π/zi；POD选取截断模态mc=2；而EMF则选取截断模态mi=5)：(a) FT方法; (b) POD方法; (c) EMD方法Fig.4 Visualization of at 200 m for case B5 integrated for 4 h obtained with three methods (Cut-off wave number for FT is kc=π/zi, cut-off mode number for POD is mc=2, cut-off mode number for EMD is mi=5)(unit：m·s-1): (a)FT method; (b)POD method; (c)EMD method

图4展示了上述3种方法针对图3a所示的w′分离所得的组织化对流，其中FT方法选取为截断波数kc=4π/zi(即截断波长λc=zi/2)，POD选取截断模态mc=2，而EMD则选取截断模态mi=5。以上主观判据的选择，是基于各方法所得的与组织化对流相关的动量通量间的最佳对应关系。在第四节中将通过针对不同判据的敏感性实验，验证分离所得结果定性一致，在合理的范围内并不依赖于主观判据的选择。对比图4与图3a，可见3种方法皆能分离出图3a所呈现的组织化结构。其中FT(图4a)和EMD(图4c)滤波所得的组织化流场较相似，相较POD结果更为平滑。POD分离的组织化流场(图4b)则相对嘈杂(即包含一定的小尺度扰动)，这是因为FT和EMD滤波在谱空间内更能做到锐截止(见第四节的谱分析)。

3 结果与讨论

3.1 非局地和局地动量的基本廓线特征

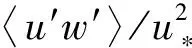
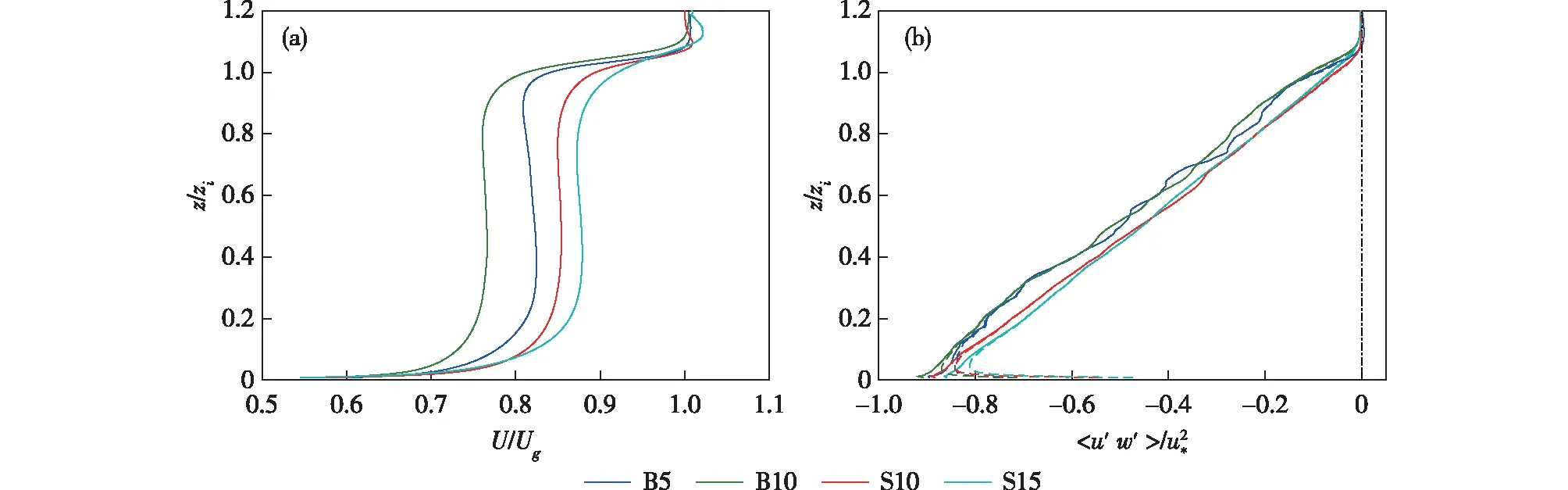
图5 经水平和时间平均的4个个例中的(a)全风速廓线与(b)x方向动量通量廓线(图b中虚线代表网格可解析通量)Fig.5 Profile of the horizontally and time-averaged full wind speeds(a) and streamwise momentum flux(b) for four cases(Dashed lines in (b) represent resolved fluxes)

(11)

分别代表组织化对流，背景湍涡和两者相互作用所产生的动量通量，其中上划线代表雷诺平均，波浪线代表滤波函数。另外，交叉项的存在取决于滤波基函数的正交性。对于正交的基函数，比如傅里叶变换滤波中所用的正余弦函数，交叉项应为0。POD和EMD的基函数(或模态)基于数据本身，而无法保证完全正交，因此也会出现量级相对较小的交叉项。图6给出了针对不同稳定度个例，采用不同流场分解方法所得的动量通量及其分量的标准化廓线，公式(11)中的雷诺平均，则由水平和时间平均〈 〉近似表示。由于总通量〈u′w′〉的个例间差异很小(见图5b)，因此由个例平均的灰色线表示总通量。边界层高度zi由水平平均的感热通量最小值确定[63]。

图6表明三种方法所得的非局地与局地通量廓线有如下定性相似之处。首先，非局地通量在混合层上半部分及夹卷层中占绝对主导，在混合层中部(z/zi≈0.4)达到最大值，而后向下逐渐减弱。局地通量则在近地层最大，并随高度单调递减，在z/zi≈0.2高度与非局地通量大小相当。其次，局地与非局地通量的廓线对于整层稳定度ζ并不特别敏感，但的确可以发现两个B个例(单体结构)和S个例(滚涡结构)间的差异，即单体结构下的非局地通量在混合层上半部分要略大于滚涡结构下的非局地通量。另外，除POD方法分解所得的两个B个例外，非局地和局地通量的符号皆与总通量保持一致，说明所有尺度的湍流都在向下输送动量。

交叉项的存在取决于基函数：FT方法的交叉项为0与理论一致；EMF的交叉项较小，说明其本征模态函数基本正交；而POD所得交叉项在B个例中较大，且在混合层中部符号为正，代表了向上的逆梯度动量输送，其是否具有物理意义尚不明确。而POD针对S个例所得交叉项则较小。以下我们将忽略交叉项的作用，而着重讨论非局地和局地通量。

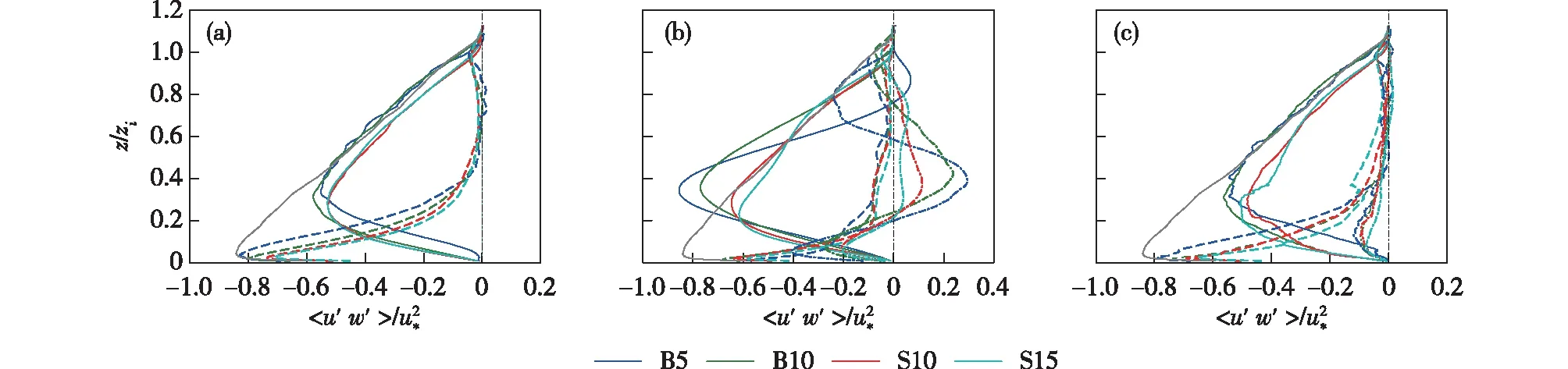
图6 四个个例中通过三种方法所得的经水平和时间平均的动量通量分量廓线(灰色线代表总通量的个例平均; 实线代表非局地通量; 虚线代表局地通量; 点划线代表交叉项): (a) FT(kzi/2π=2); (b) POD(mc=2); (c) EMD(mi=5)Fig.6 Profiles of the horizontally and time-averaged decomposed momentum flux with three methods(Gray line represents case-averaged total flux. Solid, dashed and dash-dotted lines represent nonlocal flux, local flux and the cross flux terms, respectively): (a) FT(kzi/2π=2); (b) POD(mc=2); (c) EMD(mi=5)

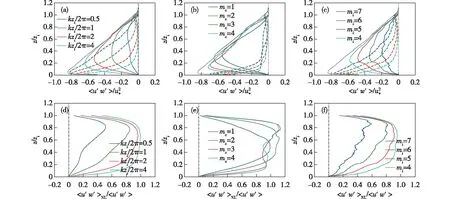
图7 S10个例中通过三种方法所得动量通量分量对主观判据的敏感性(a—c)以及非局地通量相对总通量的占比廓线(d—f)(a—c中灰色实线代表S10个例的总通量; 实线代表非局地通量; 虚线代表局地通量; 均经过水平和时间平均):(a、d) FT方法; (b、e) POD方法; (c、f) EMD方法Fig.7 Profiles of the horizontally and time-averaged decomposed momentum flux by three methods with different subjective criterion (a-c) and profiles of the corresponding ratio of non-local flux over total flux (d-f)(Gray line represents total flux of case S10; Solid and dashed lines represent nonlocal flux and local flux respectively in a-c): (a，d) FT method; (b，e) POD method; (c，f) EMD method

由于图6中的廓线是基于主观分离方法所得，其结论或依赖于各方法中所采用的主观判据。因此这里开展主观判据的敏感性实验，以检验各分离方法中的主观判据对所得的非局地和局地通量的影响。对于FT方法，选取四种截断波数(kzi/2π=0.5、1、2、4)，对于POD方法，则选取四种截断模态数(mc=1、2、3、4)，对于EMD则选取四种截断本征模态数(mi=7、6、5、4)，并计算非局地与局地动量通量。图7给出了针对S10个例的敏感性实验所得的非局地与局地通量廓线，及非局地通量相对总通量的占比廓线，其他个例因结果类似而不再展示。图7表明FT和EMD方法皆展现出较强的判据依赖性，所得的非局地通量随着滤波器的低通量减小而减小，局地通量则随之增大。尽管如此，在FT方法中，即便标准化的截断波数达到0.5(对应2zi的截断波长)，其诊断的非局地通量在混合层中依旧可达总通量的40%。同样对于EMD方法，非局地通量的贡献虽然随mi的变大而减少，但其在总通量中的占比也同样不可忽视。POD方法所得的通量廓线，在0.4zi高度以上对判据几乎不敏感，这说明其分解的第一模态已经几乎包含了混合层中上部的所有扰动能量。而在0.2zi高度，非局地通量随更多模态的加入而逐渐变大。

参照图6的廓线，并结合图7的敏感性实验结果，针对对流边界层中的非局地和局地通量特征，可以得出以下定性结论。首先，非局地通量是总动量通量的重要组成部分，尤其在混合层中部以上，非局地通量对总动量有显著的贡献。其次，非局地与局地通量的方向在边界层内各个高度皆与总通量一致，三者皆向下传输动量。最后，非局地与局地通量的分配与组织化对流的形态有一定关联，在个例包含的四种稳定性区间内呈现较弱的敏感性。

3.2 动量通量的谱分析

在获得局地和非局地动量通量的廓线特征后，为了进一步探究对流边界层中w′与u′的空间结构关系，我们首先在各高度层计算两者的相关系数ρu′w′，并以其绝对值|ρ|来度量湍流传输效率，|ρ|=0和1分别代表了无效和高效的湍流传输。图8中展示了|ρu′w′|的垂直廓线，同时也给出了w′与θ′的相关系数|ρw′θ′|以作比较。如图8所示，|ρu′w′|在近地层最大，并随高度递减。S15个例中，0.2zi高度以下|ρu′w′|的降低可能与模式分辨率相关，需在未来工作中利用更高分辨率的模拟结果进一步验证。在稳定度方面，|ρu′w′|随稳定度参数ζ的下降而快速提升，说明越接近中性层结，动量的传输效率越高。相比之下，垂直感热通量的相关系数|ρw′θ′|在近地层和混合层中，都始终要高于动量。|ρw′θ′|随稳定度的变化相对平缓，且变化趋势与|ρu′w′|恰好相反。由图8中|ρu′w′|和|ρw′θ′|的相对大小，说明了对流边界层中热量的混合效率要高于动量，这和大多数边界层方案中，在对流条件下热量的湍流混合系数要大于动量(即湍流普朗克数Pr<1)一致。另外，|ρu′w′|和|ρw′θ′|随稳定度变化的相反趋势，及两者廓线的垂直变化率都指出组织化对流会促进热量传输，但抑制动量传输。在组织化对流旺盛发展之处，如加热较强，或在混合层中，都对应|ρu′w′|的减小和|ρw′θ′|的增大。而在组织化对流受抑制的情况下，如加热减弱，或在风切变主导的近地层中，|ρu′w′|增大而|ρw′θ′|减小。

图8 4个个例的动量传输效率(实线)和热量传输效率(虚线)廓线Fig.8 Profile of the momentum (solid line) and heat (dashed line) transport efficiency for four cases

Gu′w′=Co-iQ

,

(12)

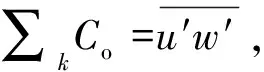
(13)

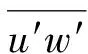
图9 S10个例中u′与w′协谱的高度—波数填色图(其中协谱经时间平均, 红色虚线为每层最具能量的尺度; 横轴中波数为水平波数)Fig.9 Time-averaged height-wavenumber contours of co-spectrum for u′ and w′ in case S10 (Red dashed line represents the scales which contain the most energy; in x-axis represent horizontal wavenumber)

基于3种分离方法，可以进一步分离组织化对流与局地湍流所对应的协谱，图10给出了0.1zi高度，针对4个不同个例，使用三种分离方法所得的协谱。首先比较4个个例的总通量协谱，可见最具能量的尺度随ζ减小而增大，这对应了滚涡的空间尺度要略大于单体[64]。其中，FT和EMD分离所得的非局地与局地通量协谱较为接近，说明EMD的滤波效果接近于锐截止滤波器。相比之下，POD所得的非局地和局地尺度则有部分重叠。

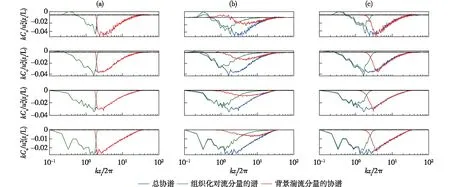
图10 0.1zi高度上u′和w′的协谱以及三种方法分解量的协谱(其中协谱经时间平均，上至下依次表示B5、B10、S10和S15个例; 蓝线代表总协谱; 绿线和红线分别代表组织化对流分量和背景湍流分量的协谱): (a) FT method (kzi/2π=2); (b) POD method (mc=2); (c) EMD method (mi=5)Fig.10 Time-averaged co-spectrum of u′ and w′, as well as decomposed field with three methods at 0.1 zi(B5, B10, S10 and S15 cases were represented from top to bottom; Blue lines represent co-spectra of u′ and w′; green and red lines represent co-spectra of the organized and background turbulence, respectively):(a) FT method (kzi/2π=2), (b) POD method (mc=2) and (c) EMD method (mi=5)

在接近边界层顶的0.7zi高度(图11c)，长波区间的Φ接近90°，对应了图2中组织化对流上半部分上升辐散的概念模型。但不同于0.1zi高度，0.7zi高度的Φ基本不受稳定性影响，在4个个例中均接近90°，这是因为在0.7zi高度处上升流虽已开始减速并伴随水平辐散，但尚未受到边界层顶强风切的影响，如图5a所示，对流结构仍能保持垂直。在高波数处，Φ同样接近0°。在混合层中部0.4zi高度(图11b)，尽管振幅较大，但Φ基本围绕在0°线左右。在这一高度，组织化对流和局地湍涡都在相对高效的承担动量通量的传输，其具体原因将留给后续研究继续展开。

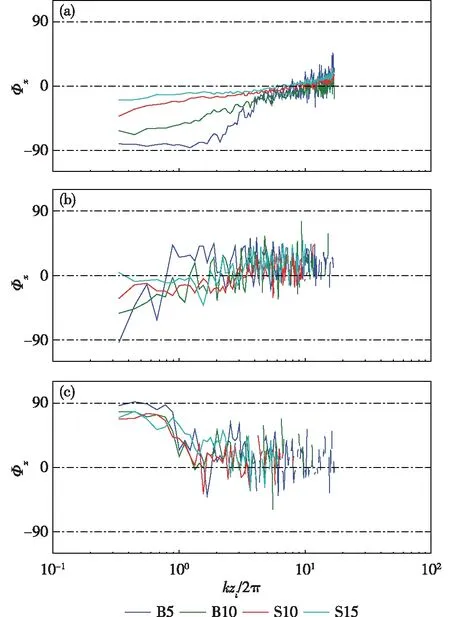
图11 3个不同高度上经时间平均的4个个例的 的相位谱: (a) 0.1zi; (b) 0.4zi; (c) 0.7ziFig.11 Time-averaged phase spectrum of for four cases at: (a) 0.1zi; (b) 0.4zi; (c) 0.7zi

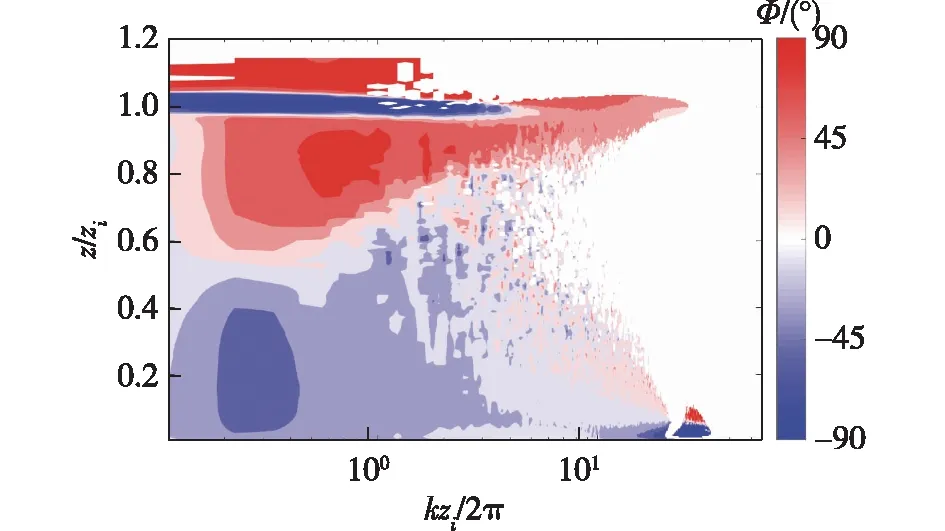
图12 S10个例中经时间平均的u′与w′相位谱的 高度—波数填色图Fig.12 Time-averaged height-wavenumber contours of phase-spectrum for u′ and w′ in case S10

图12给出了S10个例的相位谱高度-波数填色图，其他个例定性一致不再展示。图12近一步验证图11所得的结论，并推广至整个边界层。除去混合层中部，长波部分在边界层下部和上部分别对应∓90°的相位差，代表组织化对流的辐合与辐散无法有效地传输动量。而波长较短的湍涡的u′和w′则近乎同相，传输效率相对高效。在混合层中部0.4zi～0.5zi的高度区间，所有波数的Φ皆接近于0°，说明组织化对流和局地湍涡都在相对高效地传输动量。

4 结论

由热力对流形成的组织化结构是日间对流边界层最显著的特征，构成了边界层内最具能量的环流。组织化对流的水平和垂直尺度皆与边界层厚度相仿，可将热量从地面传输至边界层顶，从而实现热量的非局地混合。而边界层内无处不在的小尺度湍涡则通过梯度扩散，实现局地湍流传输。相比热量，组织化对流对动量的传输作用及机制尚不明确，现有的边界层方案中，也鲜有考虑非局地动量通量。本文针对对流边界层内的动量传输，以高精度大涡模拟数据为研究资料，定量分析了在不同整体稳定度条件下，组织化对流与背景湍流所输送的动量通量的基本廓线特征。并在此基础上，基于谱分析，初步探讨了组织化对流结构对动量传输的影响。得到如下结论：(1)利用傅里叶变换、本征正交分解和经验模态分解3种滤波方法分离边界层内的组织化结构，并对3种方法各自的主观判据开展敏感性试验，以检验结果的稳定性。研究发现，3种方法都能实现组织化湍流和背景湍涡的尺度分离。其中，FT和EMD方法所得的组织化对流统计特征较为接近，与POD略有不同。(2)3种分离方法所得的结果一致指出，组织化对流相应的非局地动量通量是边界层动量传输的重要部分。尤其在混合层中，非局地动量通量占主导地位，而在风切变较大的近地层中，动量通量则主要通过小湍涡带来的局地通量实现。从整体效果来看，边界层稳定度对非局地和局地通量的分配影响不大，两者的廓线基本不随稳定度变化。(3)通过相关性系数的计算，验证了动量通量的传输效率要低于热量通量，而效率的降低在组织化对流旺盛发展的环境条件和高度区间内尤为明显。进而对动量通量进行了的协谱和相位谱分析。发现动量通量在近地层主要由小尺度湍涡贡献，而随着高度增加，动量通量的含能尺度也随之增大。在混合层中上部，动量通量则主要由组织化对流承担。通过相位谱分析发现，组织化对流所对应的u′和w′在边界层上下分别对应了±90°的相位差，无法传输动量，可能是造成边界层内动量传输效率低于热量的主要原因。而随着波数的增加，u′和w′的相位差在约0.5zi～0.2zi的波长区间内迅速减小，在更小尺度上接近于0，代表了相对高效的湍流动量混合效率。而整体稳定度对边界层组织化结构也有显著影响，随风切的增强和加热的减弱，u′和w′组织化对流场的相位差也随之减小，以实现更高效的非局地动量传输。

综上所述，对流边界层内的组织化环流对动量传输的效率较低，但其造成的非局地动量通量依旧是总通量的重要部分。结合对流边界层的风廓线和动量通量廓线特征可知，基于梯度扩散的边界层方案无法对动量通量进行准确的参数化。在边界层方案中有必要引入非梯度扩散型的修正项，以参数化非局地动量通量，同时必须考虑整体稳定度对组织化结构传输效率的影响。