智慧农业水田作物网络化精准灌溉系统设计

鲁旭涛，张丽娜，刘 昊，智超群，李 静

（1. 中北大学机电工程学院，太原 030051；2. 中北大学信息与通信工程学院，太原 030051；3. 中北大学电气与控制工程学院，太原 030051）

0 引 言

农业是一个国家的立国之本，农业的发展水平也在某种程度上反映出一个国家的国力。伴随着世界人口的急剧增长，世界农业生产成就也十分显著。而中国作为一个农业大国，2020年中国基本农田面积约为106 666 667 hm2，但是目前多数农田依旧采用漫灌等粗放型灌溉方式进行灌溉，在很大程度上造成了水资源的浪费，并且不利于作物的生长。在水资源日益短缺的背景下，研究一种合理的灌溉方式是大势所趋，伴随着科技的发展，精准灌溉成为人们研究的一项热点[1-3]。特别是水田作物，对水位精准控制的需求尤为突出[4]。

对于精准灌溉的研究，目前国内外主要集中在硬件设计、算法模型设计两大层面[5-9]。其中，在硬件层面，专家学者聚焦灌溉系统的优化设计及灌溉参数采集研究等[10-12]。例如，有学者提出一种基于智能精准灌溉平台的线性灌溉系统，有效降低了灌溉量突变对作物的影响[13]；也有学者构建了高分辨率灌溉面积遥感监测系统，对农田灌溉进行监测[14]。而在算法模型设计层面，主要集中在模型设计及控制决策方面[15-18]，有研究采用基于贝叶斯最大熵和多源数据判断作物的需水量[19]；也有研究从灌溉精确度出发，提出了一种地表灌溉的决策支持系统[20]；此外，有专家将人工智能技术应用到灌溉决策中，提出了一种基于人工神经网络的精准灌溉系统，通过系统不断的学习来做出灌溉决策[21]；还有学者设计了一种节水灌溉管理及决策系统，降低了水资源浪费[22]。

综合上述国内外专家学者的研究，目前精准灌溉系统设计主要存在如下几个方面的问题：

1）灌溉系统底层设备部署的灵活性差：水田作物生长环境复杂，现有灌溉系统底层设备多采用有线通信方式，为设备部署、回收及维护方面带来很大挑战；一些基于无线通信的灌溉设备，其通信网络构建多采用

2）灌溉系统通信网络的连通性、能耗性差：目前通信节点无序部署或随机部署再调整的方式，缺乏模型及理论依据，造成通信网络节点脱节、通信能耗高的问题；

3）灌溉系统决策终端智能化程度不足：现有灌溉系统缺乏智能系统的决策或是采取低智能的决策方案，具有资源利用率过低、能耗高的缺陷，且需要自动化设备的重复开启，在增加设备能耗的同时，对设备寿命也有很大影响。

因此，本文设计了网络化水田作物精准灌溉系统，运用传感器技术、嵌入式系统技术、无线组网技术及人工智能理论，综合利用自然降水以及精准灌溉策略，实现在保证作物生长水位最优的前提下，减少无效灌溉，避免了水资源的浪费，为水田作物网络化灌溉提供参考。

1 网络化水田作物智能精准灌溉系统设计

1.1 套件设计

1.1.1 智能灌溉系统总体架构

本文针对水田作物复杂生长环境下，对灌溉系统的部署灵活性差及其网络连通性差、能耗性差等挑战，设计了水田智能灌溉系统，其总体架构如图1。该总体架构主要由数据采集节点、灌溉控制节点、手持控制终端、PC控制终端及无线智能通信节点五大部分组成。该系统基于无线通信的方式，通过加装太阳能发电装置，可灵活部署于水田区域。

其中数据采集节点主要负责水田作物生长环境监测，主要包括水位数据传感器、风速传感器、水温传感器及降雨传感器，传感器采集到数据后经过Arduino NANO MCU模块进行处理后，由通信模块进行转发，数据采集节点架构如图1a所示。

灌溉控制节点负责控制电磁阀的开闭，以达到精准灌溉的目的。主要由灌溉电磁阀、排水电磁阀、流量计、MCU模块及通信模块组成，灌溉控制节点架构如图1b所示。

手持控制终端便于在户外环境下，观察水田作物环境参数、手动控制阀门开闭等操作。主要包括3.5寸触摸屏、MCU模块及通信模块组成。手持控制终端架构如图 1c所示。基于中继理论的无线智能通信节点，主要适用于大范围、远距离灌溉通信网络构建。主要包括MCU模块、通信模块及太阳能供电模块。其架构如图1d所示。

PC控制终端主要负责数据的处理存储、实时显示及灌溉控制、灌溉决策。本文采用Labview+Matlab的思路，进行PC端控制平台设计。其中，利用Matlab软件设计了基于模糊控制理论的灌溉决策系统；利用Labview软件设计了数据处理、显示及灌溉控制平台，其架构如图2所示。

整个系统控制终端工作流程如图3所示。

1.1.2 智能灌溉系统通信网络构建

当农田面积扩大时，所需要的灌溉节点、数据采集节点规模也随之增大。设计合理的通信网络结构，是保证大量数据实时可靠传输、降低通信网络能耗以及降低资金投入的必要技术手段。对此，本文设计了基于中继理论的分层式智能灌溉通信网络。其结构如图4所示。数据采集节点及灌溉节点的信息传输，首先由其对应的通信中继节点进行转发至汇聚节点，再由汇聚节点传输至控制终端。智能灌溉系统实物如图5所示。

1.2 模型建立

1.2.1 精准灌溉通信网络节点最优部署模型

为避免歧义，本文根据实际情况，对精准灌溉通信网络节点最优部署做出如下定义：本文所述网络全连通是指，灌溉网络内所有节点均处于通信网络覆盖范围内，不存在脱节、丢包等问题；所谓最优部署是指以相对最少的中继节点投入数量、最低的通信能耗实现精准灌溉通信网络全连通。

本文以节点一周内平均数据量为权重，确定节点在部署过程中所占权重。当若干个灌溉控制节点、数据采集节点所对应的中继节点被确定，则这些节点的数据传输仅能通过此中继节点进行转发。基于上述定义，建立精准灌溉通信节点最优部署模型。

1）精准灌溉系统通信网络全连通模型

在三维空间下，任意两个通信节点i和j的坐标为（xi,yi,zi）和（xj,yj,zj），那么这两点之间的距离dij可表示为

依次确定灌溉控制节点、数据采集节点、智能通信中继节点、信息汇聚节点的传输距离ra、rb、rc、rd。若两节点i、j之间的距离dij满足式（2），则称其建立连通关系。

在此基础上，任意两个节点Si和Sj的连通性Cij如式 （3）所示：

当网络内所有通信节点均建立连接时，称该网络为全连通网络，即

2）通信网络能耗评估模型

无线网络通信能耗取决于数据量和节点之间距离。当两节点间距离为d，发送数据包大小为k时，发送能耗ET为

式中Eelec表示发送或接收1个字节数据能耗，Eamp表示发送过程中放大1个字节数据能耗。

对应接收能耗ER为

则完成一次通信能耗为

式中ERX、ETX分别为信息接收能耗和信息发送能耗。

当数据采集节点数量、灌溉控制节点数量、智能通信中继节点数量分别为na、nb、nc时，整体通信网络能耗Esum计算如下：

式中Eac表示所有数据采集节点到对应中继节点通信能耗；Ebc表示所有灌溉控制节点到对应中继节点通信能耗；Ecd表示所有通信中继节点到汇聚节点的通信能耗；na、nb、nc分别表示数据采集节点、灌溉控制节点及中继节点数量；分别表示第i、j、l个节点对应的信息量。

3）精准灌溉系统通信网络节点最优部署模型

公式（10）含义为在满足通信网络全连通的约束条件下，整体网络通信能耗最低。

1.2.2 精准灌溉系统最优灌溉决策模型

最优灌溉决策定义如下：在一个固定周期内，系统综合利用自然降水，以最少的灌溉量及排水次数实现作物生长水位保持在最适生长阈值内。为实现此目标，本文建立了作物耗水预测模型、降雨预测模型及最优灌溉模型。

1）作物耗水预测模型

单位日内的耗水量Wcd主要由作物蒸发蒸腾量ETd和农田渗透量INd组成[23]，即

对于作物蒸腾量的计算，本文采用经联合国粮农组织修正后的彭曼（Penman）公式[24]。

式中D为温度-饱和曲线在处的斜率，kPa/℃-；Rn指净辐射，MJ/(m2·d)；G指土壤热通量，MJ/(m2·d)；γ为温度计常数，kPa/℃；T指日平均气温，℃；U2指2 m高处风速，m/s；ea指饱和水汽压，kPa；ed指实际水汽压，kPa。

在求得作物参考蒸发蒸腾量的情况下，利用作物系数Kc对ET0进行修正：

式中Kc不仅仅因作物种类而异，而且在作物不同生长周期内取值不同，具体取值在本文参数设定环节进行说明。

2）降水预测模型

本系统通过WEB端对天气预报数据进行提取。主要提取内容有：温度值、日照、风速及降水情况。

由于自然降水到地面后会有部分通过地面径流及深层渗透流失。因此本文采取以下公式计算有效降雨量（mm）P0：

式中α为有效降水系数，与降雨延续时间及强度等因素有关；P为气压，kPa。

3）最优灌溉模型

首先，确定作物生长周期内最佳含水率S的区间θmin、θmax，作物生长周期内水田最大蓄水量θc（mm）及实际灌溉量rθ（mm）。

进一步可得出作物的生长水量平衡模型如下：

其中S∈[θmin,θmax]，即有效降水量与灌溉量之和去掉作物生长耗水量之后与作物最佳含水率S（mm）之差处于平衡。

则在第i日的灌溉量irθ（mm）为

此外，当水田水位的值超过最大蓄水量cθ时需要启动抽水电磁阀进行排水，排水模型建立如下：

式中排水量E为当前农田水位与未来降水量之和减去最大蓄水量。只有当θp＞θc时方可触发排水模型。

本文中最优灌溉是指在某一天数为n的周期内，系统利用降水，以最少的灌溉量及排水次数，使得作物生长含水量最优，可以表述为

1.3 精准灌溉控制系统设计

1.3.1 系统架构设计

通常控制系统的架构主要由如下部分组成：模糊变量的定义、输入输出数据模糊化、知识库以及逻辑判断[25-26]。将当前水位、未来降水量、未来蒸腾量作为系统输入参数，通过模糊控制器经过一系列运算之后，进而将排水量、灌溉量作为输出变量精确输出。本文所设计的模糊控制系统架构如图6所示。

1.3.2 变量模糊化

首先将所有输入输出变量分为5个等级：特小、略小、中等、略大、特大。其次，针对不同输入及输出建立与之对应的模糊子集。最后，针对子集内所有参数进行模糊控制规则设计。模糊变量子集如表1所示。

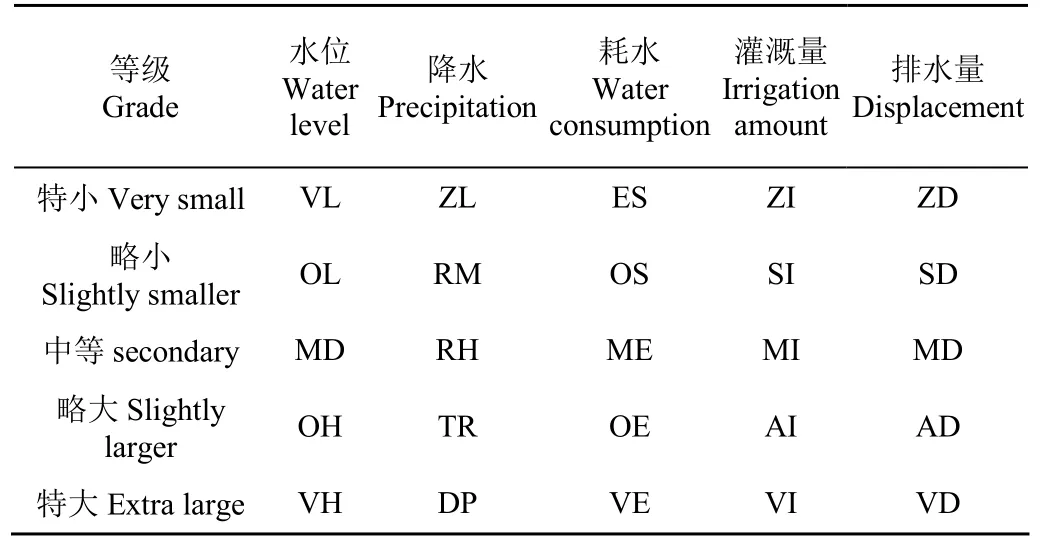
表1 模糊变量子集Table 1 Fuzzy variable quantum set

1.3.3 隶属度函数

本文选取三角形隶属度函数µx作为模糊子集的隶属度函数。

式中x为自变量，参数a和c对应三角形下部的左右两个顶点，参数b对应三角形上部的顶点。

1.3.4 模糊控制规则

通常情况下，同一区域的排水电磁阀与灌溉电磁阀的开闭情况存在如下关系：当灌溉电磁阀开启时，排水电磁阀通常处于关闭状态；反之，排水电磁阀开启时，则灌溉电磁阀关闭。因此，本文分别设定了灌溉量清零的模糊量I0及排水量清零的模糊量D0，当模糊系统执行I0或D0指令时，分别表示将灌溉/排水设备不动作。

首先，进行模糊控制目标语句设计，确定模糊控制规则，具体如表2所示。

表2 模糊控制规则Table 2 Fuzzy control rules

其次，依据前文模糊语句格式及模糊控制规则表，进行模糊控制规则设计。本文共设计模糊规则125条，其中包括设备不动作规则67条、灌溉设备动作规则13条以及排水设备动作规则45条。

模糊控制规则变量关系图如图7。其中C-Water level表示当前水位、F-Precipitation表示未来24 h有效降水量、F-Water consumption表示未来24 h耗水量、Irrigation amount表示灌溉量、Displacement表示排水量，单位均为mm。

2 精准灌溉通信网络节点部署

2.1 通信网络节点部署仿真算法

现有的对于精准灌溉系统无线通信网络节点的部署方案，多采用基于随机部署后再调节或基于简单模型求解部署的策略。前者在网络连通性、网络能耗性方面难以得到保障；而后者，存在模型考虑参数较少或所采用的求解算法本身存在收敛性差、全局性差的缺陷。因此，本文在所建立的部署模型的基础上，采用基于维诺图所改进的飞蛾扑火优化算法对该模型进行求解。

飞蛾扑火优化算法（Moth Flame Optimization，MFO），是由Sayedali Mirjalili于2015年提出的一种智能优化算法。基于维诺图改进的飞蛾扑火算法（Voronoi Moth Flame Optimization，VI-MFO），是通过引进维诺图的刨分特性来提升MFO算法的搜索寻优速度。研究表明[27]，该算法智慧农业通信网络节点部署中取得了比蚁群算法（Ant Colony Optimization，ACO）等群体智能算法更优的结果。因此，本文采用此算法进行精准灌溉通信网络节点部署仿真，算法的基本流程如图8所示。首先，根据实际需求，部署数据采集及排灌设备（统称为基础节点）；其次，通过建立空间坐标系确定基础节点坐标，对基础节点进行维诺图刨分；然后，以信息量为权重确定中继节点服务范围，并进一步构建节点多面体；最后，利用MFO算法的寻优策略，寻找通信节点的最优部署位置。

2.2 参数设定

灌溉节点、排水节点以及数据采集节点的分布受节点的安装位置、节点本身特性等因素影响，其位置分布无规律性。本文结合实际情况，针对不同需求，对不同节点类型数量、节点一周内产生信息量进行了评估计算，得出具体参数如表3所示。

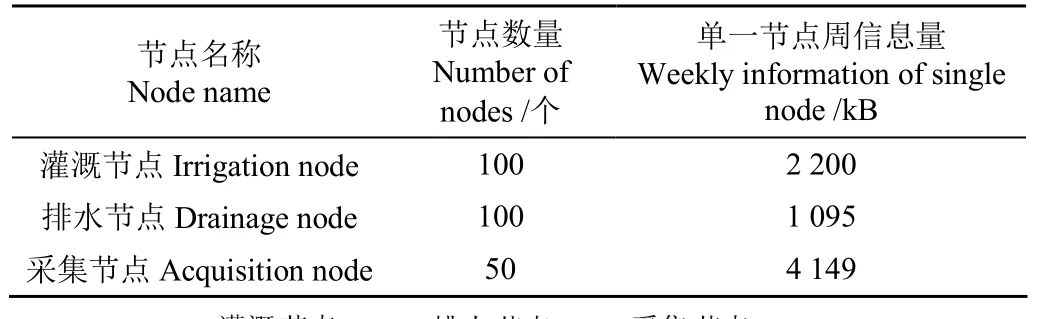
表3 节点信息量设定Table 3 Node information setting

进一步建立空间坐标系，试验环境设计在一个10 km×10 km×0.001 5 km的三维空间内。不同类型节点的分布三维图及热图如图9所示。节点能耗、节点覆盖能力及算法参数设定值如表4所示。

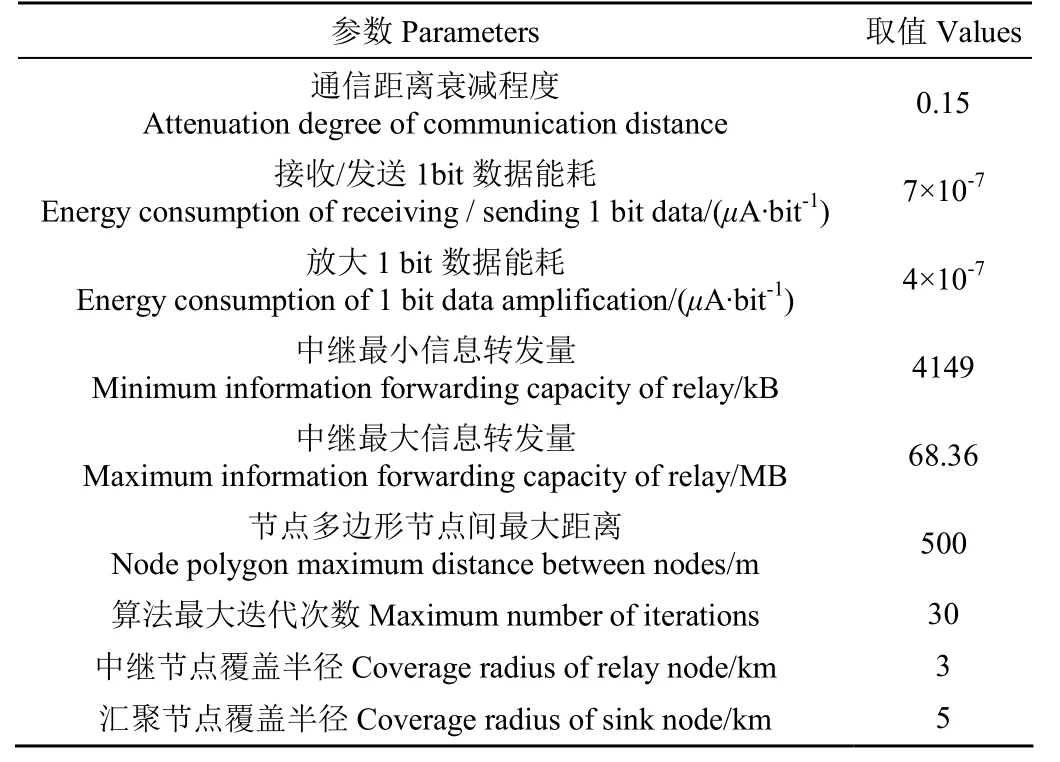
表4 节点部署参数设定Table 4 Parameter setting of node deployment

2.3 仿真结果与分析

在上述参数设置的基础上，采用计算机配置为：Intel i5-8550U CPU、8GB运行内存，编程软件为Matlab2017b的环境下进行仿真，结果如下。

1）在本文所述方案下，共使用中继节点9个，各中继节点对应基础节点（灌溉节点、排水节点、采集节点的统称）如图10所示。

2）在此基础上继续求得汇聚节点部署位置，最终构建智能灌溉系统分布式信息传输网络结果如图11所示。

3）进一步求得节点间距离矩阵如图12所示，汇聚节点到中继节点的最大距离为5.2 km；中继节点到对应基础节点的距离也均小于2.5 km，求解结果满足本文所述的全连通网络定义。

4）最后求得中继节点及汇聚节点各自数据量分布情况，具体如图13所示。图中所有中继节点均处于同一等高线上，表明所有中继节点所承载的数据转发量差距较小。这一结果能够有效避免由于能耗不均所带来的部分节点生存周期过短、后期维护复杂的窘境。进一步体现出本文部署策略及算法的性能。

3 精准灌溉系统性能测试与结果分析

3.1 性能测试方法

3.1.1 设计指标及灌溉目标设定

系统模拟江苏南京地区中稻灌溉情景。中稻生长集中在5—9月，这期间耗水及降水为一年中最为突出，更能检验灌溉系统的性能。

参考《自动气候站观测规范》（GB/T33694—2017）、《环境监测信息传输技术规定》（HJ660—2013）、《农田信息监测点选址要求和监测规范》（GB/T37802—2019）及江苏省《水稻节水灌溉技术规范》（DB/32T 2950—2016）[28]，确定灌溉系统设计指标，并结合实际情况进行参数设定。

本文所涉及的所有参数及设定方案如下：

1）农田渗透量

农田渗透量针对旱地时，前期灌溉渗透量较大，且渗透量与土壤成分有很大关系。而水田在灌溉后，土壤含水率饱和，渗透量维持在一个较小的范围内。本文假定试验土壤含水率已经饱和，取渗透量（INd）为

0.065 mm/h。

2）有效降水系数

降水系数与降水持续时间及降水强度有关。按照降雨量将降雨情况分为以下6档：日降雨量Pr＜10 mm为小雨、10～25mm为中雨、＞25～50 mm为大雨、＞50～100 mm为暴雨、＞100～250 mm为大暴雨、＞250 mm为特大暴雨[25]。其中，小雨的有效降水系数α为0，中雨和大雨的α为0.8～1.0，暴雨、大暴雨以及特大暴雨的α为0.7～0.8。其中，有效降雨量为降水量与有效降水系数的乘积。

3）作物系数与作物的种类、地理位置、生长周期及当前月份有关。中稻作物系数5—9月依次为1.03、1.35、

1.50、1.40、0.94[29]。

4）水位指标

水位指标主要包括作物最佳生长水位上下限θmax、θmin、田间最大蓄水量θc。最大蓄水量表示降雨后田间可以留存的最大水量，且水田保持最大蓄水时间不得超过6 d[30]。

所有指标与灌溉方式及作物生长周期有关。本文选择水稻返青期作为试验周期，选取浅湿灌溉的节水方式[31]。在此背景下，结合实际情况，40 mm为作物最佳生长水位上线，20 mm为作物最佳生长水位下线，60 mm为田间最大蓄水量[32]。

3.1.2 试验环境参数设定

本文以江苏南京地区6月天气为例，进行系统运行参数设定，其中，纬度为31°19′39″N，海拔为25 m，纵坐标分表高度为2 m，日序数为153～183（6月），初始水位25 mm。测试中风速、高低温、降水量等气象参数值来源于2020年6月南京市的天气预报，该预报值以72 h/次的频率，逐次获取并统计量化得到。其中，6月气温变化如图14所示。

3.2 仿真试验结果

按照表5参数设定，对本文设计的智能灌溉系统进行测试。将所有参数输入灌溉系统，得出稻田每日耗水量、有效降水量（图15a）；进一步得出稻田自然水量理想变化曲线，如图15b所示。

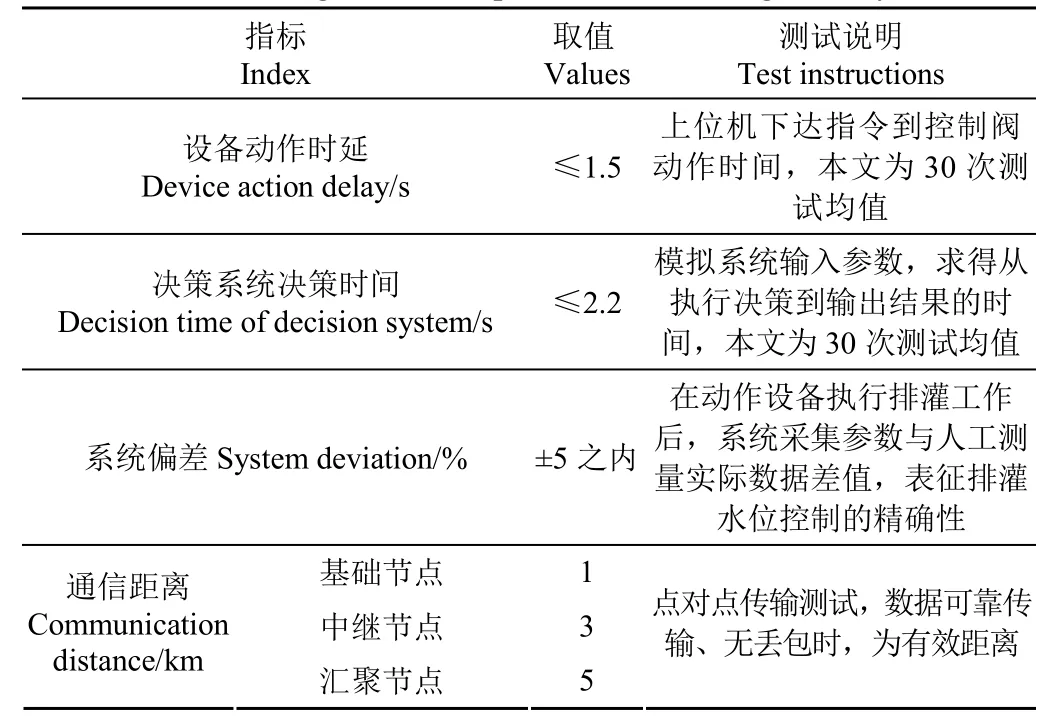
表5 灌溉系统设计指标要求Table 5 Design index requirements for irrigation system

从图15a可以看出，稻田耗水量随气象参数变化的变化而改变，特别是在6月4日最高气温达到月最高值时，耗水量也随之达到月最大值；此外，综合稻田每日接收到的有效降水量与稻田每日耗水量与进水差值变化可以看出，稻田水量随着降水量与耗水量之间的差值，产生自然变化，30 d内稻田自然水位已经严重偏离稻田蓄水范围。以上结果及变化曲线符合自然规律，验证了系统模型的有效性。

进一步模拟传统的非智能灌溉方式（当水位低于作物生长水位时执行灌溉指令；水位高于固定水位值时执行排水指令）进行灌溉控制的仿真结果如图16所示。

由图16可知，非智能灌溉方式采用水位低即灌溉、水位高即排水的策略，这种灌溉方式下，虽然将水位控制到了合理范围内，但是调节过于频繁，造成了资源的浪费。进一步求得非智能灌溉方法在6月灌溉/排水次数（动作日期）、每次灌溉/排水量（动作量，mm），如表 6所示。此外，本文将系统完成灌溉后24 h内由于降水原因造成水位超上限，定义为无效灌溉动作；系统完成排水后24 h内由于作物耗水原因造成水位低于下限，定义为无效排水动作。进一步得到非智能灌溉无效动作次数与有效动作次数。

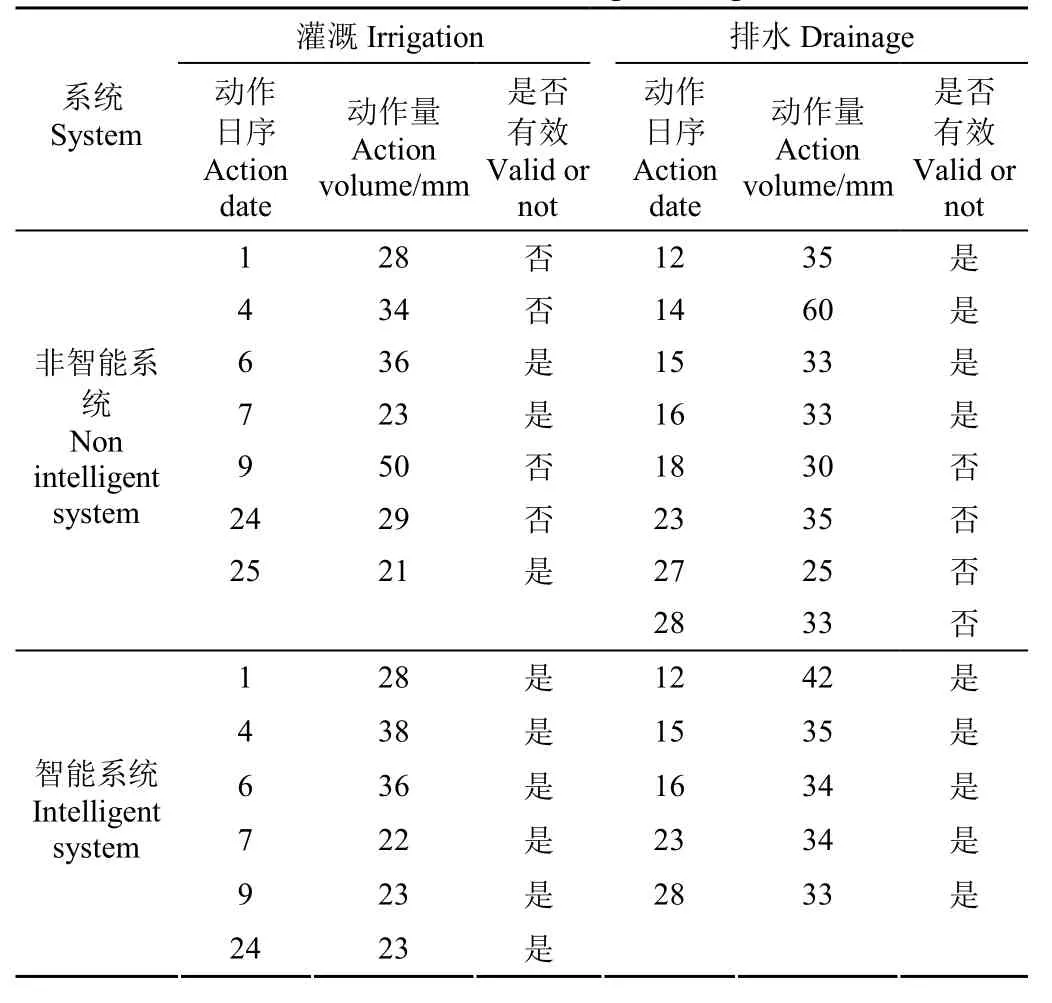
表6 不同灌溉系统灌溉效果对比Table 6 Statistics of non-intelligent irrigation results

综上，非智能灌溉系统总计执行灌溉7次、排水8次，共动作15次，有效动作率（有效动作次数除以总动作次数）仅为53.33%。

在相同参数下，利用本文所设计的智能灌溉系统进行测试，测试结果如图17所示。在智能灌溉系统的控制下，稻田水位始终处于安全阈值内，其中有22 d处于水稻生长周期内最适水位；仅有1 d处于低水位区；有7 d处于高水位区且每次持续时间最大为48 h，不会对作物生长造成损害，仿真试验结果处于系统参数设定阈值内。在30 d内智能灌溉系统共工作11次，包括执行灌溉6次、排水5次，灌溉总量和排水总量分别为177.41 mm、184.26 mm，有效动作率达到100%。可以看出智能灌溉系统与非智能灌溉系统相比，在减少动作次数26.67%的基础上，减少灌溉量40.82%、减小排水量33.89%。

3.3 智能灌溉系统田间实际应用效果

本文通过实物测试，验证了所述智能灌溉系统的性能，通过模拟6月6日—6月12日的气象参数对系统进行测试，验证表5中各项指标参数，测试环境如图18；表7为系统性能指标测试结果；表8为系统测试结果。

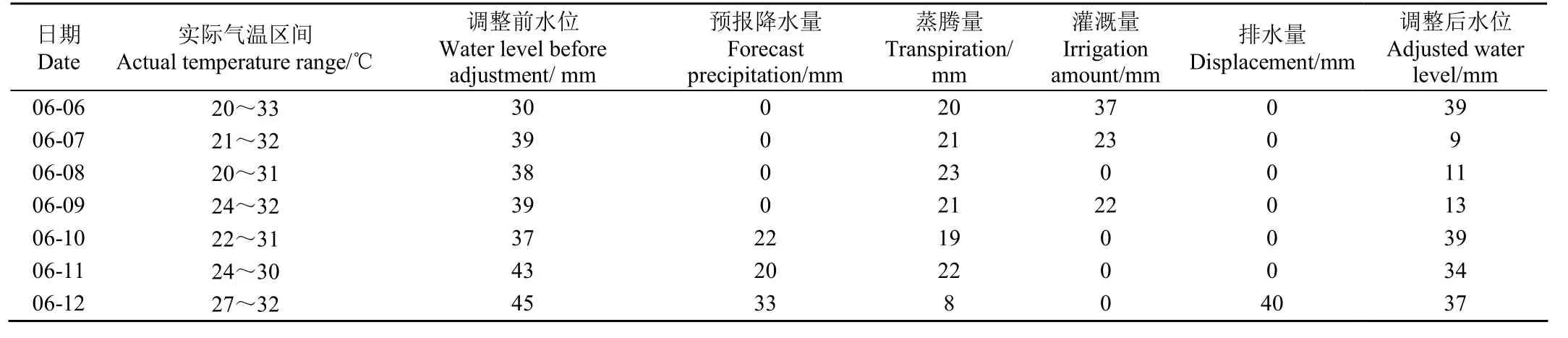
表8 智能灌溉系统测试结果Table 8 System test results of intelligent irrigation system

经实际测试，本文所设计的智能灌溉系统各项功能正常，从表7可以看出，各项功能指标均满足表5中的相关设计要求。

通过以上结果可以看出，在智能灌溉系统的调控下，水位始终保持在作物最适生长区间内。结合表6可以发现，系统测试结果与仿真结果最大偏差为：灌溉量1 mm（6月6日）、排水量2 mm（6月12日），测试结果符合预期。造成该偏差的主要原因是实际环境下传感器精度对数据精确性造成了一定的干扰以及一些不可控的必然误差。

4 结 论

本文设计了一种针对大规模水田作物灌溉的网络化灌溉系统，通过设计灌溉基础设备、构建无线灌溉通信网络、建立精准灌溉模型及灌溉决策系统，实现了将无线传感器网络技术、物联网技术、单片机技术以及模糊控制技术相融合的网络化智能灌溉系统。该系统采用无线通信方式，不受大量线缆束缚，可灵活部署于水田区域。仿真结果表明，灌溉系统通信网络在满足全连通的基础上，通过综合利用自然降水的调控策略，使得灌溉设备动作频次降低了26.67%，灌溉量及排水量分别减少了40.82%、33.89%。田间应用测试结果表明，系统各部分功能模块工作正常、实测结果与仿真结果的排灌量最大偏差控制在2 mm以内，符合预期。但由于系统过于依赖气象预报参数的置信度，下一步工作将从气象预报参数与传感器参数数据融合角度出发，结合机器学习理论，进一步提升系统决策的精确度。