基于遗传算法的液肥变量施肥控制系统

田 敏，白金斌，李江全

（石河子大学机械电气工程学院，石河子 832003）

0 引 言

变量施肥是精准农业发展过程中一个重要的研究领域[1-5]，该技术能够很好地解决劳动强度大、施肥作业效率较低以及人工施肥的不均匀等问题。国内外研究表明，变量施肥技术可使作物平均增产8.2%～19.8%，化肥施用量减少约20%～40%，土壤质量也会有所改善[6]。肥料形态对于施肥效果的影响也较大，一般而言，液态肥料比固态肥料的吸收率高约50%[7]。在中国农田灌溉中，灌溉用水的利用率不到35%[8]。

早期在变量施肥控制系统的研究中，针对大田滴灌、喷灌等固定地点的液肥变量施肥控制系统研究占多数，而针对大田移动式施肥的研究时间不长，但进展迅速[9-10]。薛秀云等[11]设计了一种基于ZigBee的液肥变量深施系统，其利用ZigBee进行组网，实现了上下位机短距离无线通信，通过控制变频泵的频率达到精准施肥的效果。该系统通过增量式PID（Proportion Integral Derivative）算法对控制系统进行优化，控制效果较好，但未考虑系统工作寿命以及实际环境中的适用性。左光焜[12]设计了一种液态肥变量注肥控制系统，该系统以轮式点状注肥机为载体，通过PID算法对控制系统进行优化，实现了良好的液态肥变量施肥效果，但控制算法较单一，其压力和流量的控制仍存在较大的优化空间。于畅畅等[13]设计的高频间歇供肥系统针对液肥点施时的高频率开关阀门而导致的压力波动进行优化，采用临界比例度法对PID算法的参数进行整定，其系统稳定性以及实际工作效果有待验证。李晓晓等[14]采用模糊PID控制器对基于PLC控制的水肥一体化试验系统进行控制优化，以实现精准调控肥液浓度，达到精准施肥的目的，但是该试验系统达到稳定状态所需时间超过40 s，且缺少试验验证。乔白羽等[15]研制了一种基于LiDAR（Light Detection And Ranging）扫描的高地隙宽幅喷雾机变量施药系统，该系统通过PWM（Pulse Width Modulation）脉宽调制实现电磁阀的控制，该研究对不同株高作物所需喷药量进行变量控制，但是激光雷达对于作物株高识别存在误差，喷雾控制存在一定误差，且误差波动同样较大。陈彬等[16]设计了一种喷杆喷雾机变量控制特性测试系统，该系统通过试验平台实现了压力、流量以及车速变化时的特性测量，平均滞后时间较小。根据以上研究可知，在液肥变量施肥控制系统的研究中，针对变频泵以及阀门的控制较多，且多数研究采用PID算法或者PWM进行阀门的优化控制，或者以PID控制为基础进行模糊控制算法以及神经网络等控制算法的研究。而在自走式或者牵引式喷雾施肥机[17-18]中，管道内流量检测反馈的快慢以及电动比例阀根据需求调整阀门开度的响应时间是变量施肥控制系统中需要考虑的重要因素[19-21]。

为了实现液肥施肥系统的变量控制，提高变量施肥的流量控制精度，本研究提出一种通过遗传算法进行优化的变量施肥控制系统，通过对施肥控制系统电动比例阀的控制以及实时流量的采集反馈过程进行建模，以模糊PID算法为基础，采用遗传算法对模糊控制规则进行优化，并进行仿真分析与试验。

1 施肥机结构与工作原理

本文的牵引式液肥施肥机整体结构由牵引式车架、自吸喷射泵、施肥喷杆、肥料箱支架、液肥箱、喷杆悬架、喷杆固定架、控制阀组、施肥管路组成，如图1所示。该液肥变量施肥控制系统搭载于牵引式拖车上，施肥喷杆作业幅宽为10 m[22]，拖车行驶速度的变化范围为1～3 m/s[23-25]。施肥喷杆由4段组成，施肥喷杆中间为喷杆悬架，悬架安装于喷杆固定架上，悬架由避震装置以及液压杆支撑，悬架的施肥高度可在0.7～0.92 m进行调节。施肥喷杆与喷杆之间以及施肥悬架与施肥喷杆之间由合页连接，可在水平方向折叠或伸展。喷雾喷头共16个，在水平方向上均匀分布，每一段施肥喷杆垂直方向下端固定有3个喷头，施肥悬架下方固定有4个喷头。控制阀组以及自吸喷射泵安装于肥箱架前段。

本文的变量施肥机采用喷杆喷雾式的水肥一体化施肥方法进行施肥。该系统控制液肥流量变化的重要部件为电动比例阀，安装于图1的控制阀组中。控制阀组中的分段阀由5个子阀组成，分段阀只控制阀门的开闭。根据本文液肥变量施肥控制系统的施肥要求，系统流量控制的原理为，依据施肥处方图给定当前田块所需施肥量，电动比例阀开度随车速的变化而变化，施肥量通过流量计检测并反馈到控制器，控制器对实时流量、当前田块所需施肥量以及实时车速进行分析比较，从而形成一个闭环负反馈调节系统，保证当前田块的施肥均匀性。该闭环负反馈控制的稳定性以及系统响应精度是影响本文液肥变量施肥控制系统施肥精度的关键因素。

液肥施肥机主要结构与性能参数见表1。

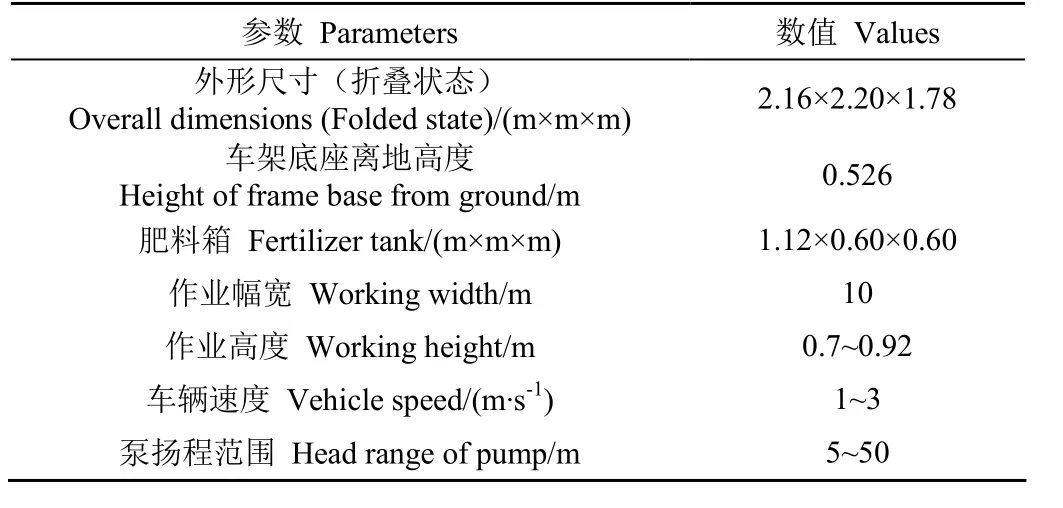
表1 液肥施肥机主要结构与性能参数Table 1 Main structure and performance parameters of liquid fertilizer sprayer

2 液肥变量施肥控制系统建模

为了优化液肥施肥系统的控制过程，降低控制系统的响应时间，对液肥施肥控制系统进行传递函数的模型建立。本文的液肥变量施肥控制系统控制模型由角速度传感器采集的实时车速作为输入，控制器经过换算后将电信号输送给电动比例阀，电动比例阀控制阀门开度，最后系统输出量为液肥流量。液肥流量通过图2控制系统框图的流量计反馈到控制器，通过控制器进行闭环负反馈控制。

根据控制系统框图的输入输出关系，得到系统的输入输出关系为

式中Q为变量施肥控制系统输出的液肥体积，L/min；为过程函数；v为车辆行驶速度，m/s；λ为输入系统的目标施肥量，依据新疆149团6连棉田的叶面肥用量，本文设定λ为35 L/hm2；l表示施肥幅宽，m，根据本文设计，l=10 m。

根据图2可知，系统反馈通道的输入量为流量计读取的实时流量，反馈通道输出到控制器的信号为电压信号，控制器将信号进行转换后与输入系统的车速以及目标施肥量进行对比调整，实现控制系统的负反馈控制。

因此，控制模型中反馈环节的函数可表示为

式中τ为反馈环节的信号传递延迟时间，s；s为传递函数进行拉普拉斯变换后的复变量，H表示传递函数的负反馈环节。

本文控制系统流量计的检测为实时进行，根据硬件条件，该反馈环节的延迟时间可忽略不计。

根据液肥变量施肥控制系统控制要求，电动比例阀为主要控制对象，选用ARAG公司的编码463020电动比例阀，其信号控制框图如图3所示。根据图3，驱动模块的输入输出均为电压信号，传递函数为比例环节加延迟环节，其关系式为

式中Ks为变换器放大系数；Uout、Uin分别表示驱动模块输出与输入的电压信号，V；G1(s)为驱动模块的传递函数。

驱动模块电压信号传输过程的延迟τ＜ 0.05 s，τ对于系统的影响可以忽略不计，因此驱动模块传递函数可表示为比例环节[26]。

在电动比例阀的直流电机中，控制信号输入为电压信号，输出为电机轴转角。直流电机的信号控制电路中包含电枢回路平衡、电机转子的电磁感应以及电机轴的力矩平衡，其平衡方程如式（5）～（7）所示。

式中t为时间，s；ua(t)为输入直流电机的电压，V；E为电机电动势，V；i(t)为电枢电流，A；Ra为电枢总电阻，Ω；La为电枢总电感，H；kε为反电势系数；θm为电机轴转角，(°)；km为电机力矩系数；M1为电机负载力矩，N·m，其中f为摩擦系数；Jm为电机转子的转动惯量，kg·m2；ωm为电机转子的角速度，rad/s。

对式（4）进行拉普拉斯变换，得到电动比例阀直流电机的传递函数，如式（5）所示。式中θm(s)为电机轴转角的拉普拉斯变换函数；Ua(s)为电机输入电压的拉普拉斯变换函数；G2(s)为直流电机的传递函数。

减速器由齿轮组组成，直流电机输出轴的转速经过减速器后作为阀芯的位移量输出。阀芯的位移X为0～19 mm，本文中阀芯的线性位移即为电动比例阀的开度。

减速器输入输出信号传递关系主要由传动比体现，控制过程为比例控制，传递函数表示为

式中i为减速器的传动比，L为传动杆导程，mm；X(s)为阀芯位移的拉普拉斯变换函数；G3(s)为减速器的传递函数。

本研究应用的电动比例阀在固定压力工况下的开度与流量为线性关系，因此流量与开度的关系可由式（7）表示：

式中G4(s)为阀门开度与流量的传递函数。

根据图3控制系统框图可知，前向通道的控制对象主要为电动比例阀，其传递函数表示为

式中G(s)为电动比例阀的传递函数。

根据控制模型以及各控制环节函数可知，本文的变量施肥控制系统的闭环反馈控制传递函数表示为

式中Gr(s)为液肥施肥控制系统的传递函数。

3 变量施肥控制模型仿真分析

3.1 模糊PID控制器设计

根据本文的变量施肥控制系统的控制要求对模糊控制器进行设计。模糊PID控制系统框图如图4所示。

模糊控制的原理是将输入输出的参数模糊化，然后根据专家经验建立模糊控制规则[27-29]，控制器根据控制规则实现模糊推理，最后采用重心法将输出参数进行解模糊得到PID参数的补偿值。

式中u(k)为控制系统的输出；为流量累计误差；K′P、K′I、K′D分别为比例、积分、微分项系数的基础值。

模糊PID控制算法中，以误差e(k)以及误差变化率ec(k)作为控制器的输入，分别以PID控制器3个参数KP、KI、KD的补偿值ΔKP、ΔKI、ΔKD作为模糊控制器的输出。经过模糊规则的推理[30-31]优化后得到PID控制器所需的参数值。

通过分析变量施肥机的工作过程，选择7个状态作为模糊控制器输入的状态变量，分别为负大、负中、负小、零、正小、正中、正大（PB、PM、PS、ZO、NS、NM、NB），各变量均采用三角形隶属度函数进行求解。

3.2 遗传算法优化模糊控制规则

合理的模糊规则以及隶属度函数能够使系统达到更加理想的控制效果。本研究通过遗传算法对系统所需模糊规则进行寻优求解。遗传算法是一种模拟达尔文生物进化论的计算模型，该算法通过自然选择和遗传学机理对数学模型进行最优解搜索。

遗传算法对模糊规则的优化流程如图5所示。

3.2.1 遗传编码

利用遗传算法对模糊控制规则进行优化时，考虑到解的数量以及运行时间，不进行隶属度函数以及论域范围的优化求解。根据模糊控制器输入输出可知，5个模糊变量分别为流量误差、流量误差变化率以及比例、积分、微分的补偿值，每个变量的论域设置7个模糊语言值。

根据模糊控制器的设计，将模糊语言值进行数字化编码，以1、2、3、4、5、6、7分别表示PB、PM、PS、ZO、NS、NM、NB。

由此得到输入变量e(k)和ec(k)的编码为一个49×2的矩阵，其式为

式中in为模糊控制器的输入值组成的矩阵。

模糊控制器输出值ΔKP、ΔKI、ΔKD的模糊语言值矩阵Y为49×3的矩阵。由此得到模糊规则数字化的矩阵为

式中rule为模糊规则数字化编码组成的矩阵。

该矩阵行向量表示的即为模糊控制规则。根据遗传算法编码要求，将3个输出变量的模糊规则重新按顺序排列为一行向量即为种群中个体的染色体长度，其长度为7×7×3。

3.2.2 适应度函数

适应度表示种群进化过程中个体对环境的适应能力。生物进化过程中，适应度低的个体存活概率小，适应度高的个体存活概率大，保留适应度高的个体后，经过多次迭代便能产生更优的个体。

因此适应度函数是遗传算法寻优的关键函数。充分考虑变量施肥控制系统响应时间、超调量以及误差等因素，选用时间乘绝对误差积分准则（Integral of Time and Absolute Error，ITAE）作为遗传算法优化的性能指标，其适应度函数表示为

式中J(ITAE)为系统运行时间乘以流量绝对误差的积分值；t为系统运行时间，s；e(t)为流量在时间域上变化的误差值，L/min。

3.2.3 遗传算子

遗传算法优化的一般步骤为

1）初始化种群；

2）计算适应度值；

3）选择、交叉、变异；

4）生成新种群。

根据遗传算法优化过程可知，在设置好遗传代数后，种群便会重复以上一般优化步骤，并不断迭代产生个体适应度更高的新种群。

“选择”的目的是将种群中的个体经过算子作用后选择出适应度较好的个体直接遗传到下一代。

“交叉”过程是随机选取2条染色体，并随机选择染色体的位置进行交换，且2条染色体随机选择的位置相同。

“变异”过程是将染色体中某个位置的值用1～7之间的一个随机数代替。

根据遗传算法参数设置原则，本文将交叉概率设置为0.8，变异概率设置为0.1。

3.3 控制系统仿真分析

3.3.1 PID控制系统建模仿真

针对所设计的变量施肥控制系统模型，通过MATLAB软件中的simulink仿真模块建立液肥变量施肥控制系统的传统PID控制仿真模型，输入的阶跃信号幅值设置为1，对PID控制器参数进行整定，分析系统输出的波形。

PID控制模型仿真过程为：在t=0时刻输入一个幅值为1的阶跃信号，设定仿真时间为30 s，并对PID控制器的KP、KI、KD进行整定调整，然后输出波形到示波器，其仿真波形如图6所示。

根据图6可知，模型响应时间为8.4 s，超调量为0.017，系统运行达到稳定前存在一定的振荡。根据经验试凑法，最终选取KP=38、KI=0.43、KD=0.01。

3.3.2 模糊PID控制系统建模仿真

在simulink仿真模块中建立模糊PID控制系统仿真模型，输入信号同样为幅值为1的阶跃信号。仿真过程为，在t=0时刻输入一个幅值为1的阶跃信号，设定仿真时间为30 s，模糊控制器输入的变量为经过模糊化处理的误差e(k)及误差变化率ec(k)，模糊控制器输出经过解模糊后的PID参数的补偿值，通过补偿值对初始参数进行优化，然后得到控制系统仿真波形。

建立的模糊PID控制系统模型如图7所示，其仿真波形如图8所示。

从图8可以看出，模糊PID控制的响应时间为7.32 s，超调量为0.04，系统运行达到稳定前有部分振荡。相较于传统PID控制，超调量增加了0.023，但是系统响应时间减少了1.08 s。

3.3.3 基于遗传算法的控制系统仿真分析

针对变量施肥控制系统建立的模型，通过MATLAB软件编程实现遗传算法对模糊控制规则进行优化仿真。以绝对误差积分准则对遗传算法优化的每一代个体进行性能指标的判断，在种群迭代达到所需性能指标时结束优化过程，若没有达到所需指标，则取最后一代种群中的最优个体作为结果进行控制模型仿真分析。

系统输入一个幅值为1的阶跃信号，然后将模糊控制器输出的补偿值ΔKP、ΔKI、ΔKD所对应的模糊语言值组成个体的染色体，并随机生成初始种群，通过遗传算法算子对种群中个体的染色体进行优化，并且使种群不断迭代到最大遗传代数。

遗传算法最优个体迭代寻优过程如图9所示。优化后的模糊规则表如表2所示。

表2 模糊PID控制规则Table 2 Fuzzy PID control rules

将优化后的模糊规则导入模糊控制器，并对控制模型进行仿真，仿真结果如图10所示。

由图10可知，基于遗传算法的模糊PID控制，系统的响应时间为4.86 s，超调量为0.038，系统运行达到稳定后存在微小扰动，相较于传统PID控制，超调量增加了0.021，但是响应时间减少了3.54 s；相较于模糊PID控制，超调量减小了0.002，响应时间减少了2.46 s。系统响应更加迅速，超调量更小，整体控制效果更佳。

4 台架试验

4.1 试验材料与平台

变量施肥试验于2020年11月以及2021年5月在石河子大学农学院玻璃温室进行。试验平台包括控制阀组ARAG 473、喷头ARAG 422、过滤器ARAG 326 9113、管路、ARAG WOLF桨流量计、电动比例阀ARAG 463、自吸喷射泵JET 5-50-1.8、控制器APC-3072、开关盒等，如图11所示。自吸喷射泵最大扬程为50 m，最高吸程9 m，最大流量83.3 L/min。控制器采用英特尔的AtomTM处理器E3845，4G DDR3L内存，5线电阻式触摸屏。电动比例阀阀芯最大口径为19 mm，0.15 MPa压力下最大流量为1 016 L/min。

试验控制对象为电动比例阀以及电磁阀，试验材料为不含固体悬浮颗粒物的清水[32]，分别对传统PID控制、模糊PID控制以及基于遗传算法的模糊PID控制进行施肥流量控制精度的测量与验证。

试验平台自吸喷射泵由220 V交流电供电，控制器以及执行机构通过开关电源将220 V交流电转换为12 V直流电后送入控制系统。试验平台高度为1.4 m，宽度为0.6 m。

4.2 系统控制精度分析

本研究中，控制系统的施肥精度通过流量误差以及车速变化工况下的流量控制稳定性和阀组响应时间来体现。引起施肥流量误差的主要位置在阀组前后，自吸喷射泵供水存在一定的误差，流量计的测量也存在误差，分段阀中每组喷头之间也会存在一定的误差。其中，流量计误差[33-35]是主要误差。产生流量误差的原因主要有：1）待测液体的电导率变化；2）流体中含有大量气泡；3）沉淀物的影响。此外，电磁流量计也会受到电磁环境等外部干扰，从而对系统精度产生一定的影响。

在本系统中，流量误差主要来源于流体。流量绝对误差表示实际流量与流量计读取的流量之间的差值，流量相对误差为绝对误差与实际流量的比值。

流量误差计算式为

式中σ0为系统流量的绝对误差，L/min；σ1为系统流量的相对误差，%；Qr为实际流量，L/min；Qt为流量计读取的流量，L/min。

4.3 结果与分析

4.3.1 控制稳定性试验

电磁流量计测量的数据显示在控制器屏幕上，而实际喷施的液肥流量则由试验测得。根据田间拖拉机实际行驶速度[36]，试验中车速通过控制器依次设定为1.5、2.0、2.5、3.0 m/s，并对每一组车速对应的流量进行测量，每组流量重复测量5次取平均值。在施肥量250 L/hm2的条件下，依据公式（1）确定这4种不同车速下的理论施肥流量依次为22.5、30.0、37.5、45.0 L/min。

对4种工作状态下系统输出的流量进行测量，每种工作状态进行3次测量，单次测量持续时间1 min，以3次测量的平均值作为该工作状态的测量流量。同时记录每一种控制算法优化后的绝对误差以及相对误差，试验结果如表3所示。

表3 系统流量控制误差Table 3 System flow control error

由表3可知，传统PID的施肥流量误差高于模糊PID以及基于遗传算法的模糊PID。传统PID的流量平均相对误差为5.19%，最大绝对误差为2.18 L/min。模糊PID的流量平均相对误差为3.40%，最大绝对误差为1.40 L/min。基于遗传算法的模糊PID的平均相对误差为1.14%，最大绝对误差为0.54 L/min。试验结果表明，基于遗传算法的模糊PID对系统流量的控制相对误差最小，与传统PID相比，相对误差减少了4.05个百分点，与模糊PID相比，相对误差减少了2.26个百分点，控制的稳定性最佳。

4.3.2 变量控制试验

变量控制试验通过数据采集卡对车速进行采集，车速由角速度传感器产生的方波信号进行计算得到，并将采集的方波信号通过可编程信号发生器进行设置与储存，试验通过可编程信号发生器模拟车速变化时的电信号，并对传统PID、模糊PID以及基于遗传算法的模糊PID进行施肥流量的变量控制试验。

试验中，液肥流量通过流量计读取，试验数据在系统运行稳定后开始记录。

速度变化工况下流量控制的试验结果如图12所示。由图12可知，在本文的变量施肥控制系统中，传统PID的流量调节平均响应时间为5.19 s，模糊PID的流量调节平均响应时间为4.12 s，基于遗传算法的模糊PID的流量调节平均响响应时间为3.21 s。从试验结果可以看出，基于遗传算法的模糊PID较传统PID控制的实际响应时间减少了1.98 s，较模糊PID控制的实际响应时间减少了0.91 s，基于遗传算法的模糊PID具有更优的响应速度和更好的流量控制稳定性。

5 结 论

本研究针对牵引式液肥变量施肥控制系统进行控制精度研究，搭建了系统控制模型，并针对传统PID、模糊PID以及基于遗传算法的模糊PID控制方式下的液肥流量控制进行仿真分析和试验，得到如下主要结论：

1）本研究采用遗传算法结合模糊PID算法对系统进行控制优化，建立了液肥变量施肥控制系统模型，利用遗传算法优化后的模糊规则对PID的参数进行优化调整，增强了控制系统的稳定性。

2）本研究分析了液肥变量施肥控制系统的负反馈调节过程，并通过MATLAB软件对控制系统进行建模和仿真分析。结果表明，传统PID控制达到稳态的响应时间为8.4 s；模糊PID控制达到稳态的响应时间为7.32 s；基于遗传算法的模糊PID控制达到稳态的响应时间为4.86 s，基于遗传算法的模糊PID响应时间最短，稳定性最佳。

3）台架试验结果表明，针对本文的变量施肥控制系统，传统PID控制的施肥流量平均相对误差为5.19%，模糊PID控制的施肥流量平均相对误差为3.40%，遗传算法优化模糊PID控制的施肥流量平均相对误差为1.14%。传统PID控制的实际响应时间为5.19 s，模糊PID控制的实际响应时间为4.12 s，基于遗传算法的模糊PID控制实际响应时间为3.21 s。基于遗传算法的模糊PID控制较传统PID控制的实际响应时间减少了1.98 s，相对误差减少了4.05个百分点；比模糊PID控制的实际响应时间减少了0.91 s，相对误差减少了2.26个百分点。基于遗传算法的模糊PID控制实际控制效果更佳。研究结果可为棉田叶面施肥或者喷药控制提供可行方案。