采用LWD-QPSO-SOMBP神经网络的拖拉机柴油机故障诊断

周俊博，朱烨均，肖茂华※，吴剑铭

（1. 南京农业大学工学院，南京 210031；2. 东台市农业机械化技术推广服务站，盐城 224246）

0 引 言

柴油机作为拖拉机的动力源，其健康状况直接影响拖拉机的性能及安全性[1]。拖拉机柴油机故障具有机理复杂多样性以及多故障并发性等特点，故障诊断已成为目前的研究难点[2]。

随着近年来人工智能的发展[3]，基于深度学习的神经网络故障诊断方法已经成为拖拉机柴油机故障诊断的重要方式[4]。其中，BP（Back Propagation）神经网络由于具有良好的非线性映射能力，被广泛应用到拖拉机柴油机故障诊断与预测中[5]。罗椿旺[6]采用BP神经网络对激光选区熔化成形件表面粗糙度进行预测，试验结果表明BP神经网络的训练误差在0.01时停止迭代，由于BP神经网络缺乏跳出局部最优解的能力，通常训练不出合适的网络模型。梁恒诺等[7]采用BP神经网络对齿爬式升船机横导向装置结构损伤进行识别，试验结果表明BP神经网络的损伤结构识别率仅为93%，在未经优化的情况下BP神经网络的泛化能力及预测能力弱[8]。基于此，有学者提出用无监督学习的方法对BP神经网络的数据做预处理[9]。周晔锡[10]采用SOM（Self Organizing Maps）神经网络与BP神经网络复合结构对中速磁浮列车悬浮控制器进行故障诊断，试验结果表明，BP神经网络在迭代1 714次时网络精度达到目标精度，而复合结构仅用609次迭代达到同等精度。

虽然SOM神经网络在BP神经网络的应用能够加快网络收敛速度，但是SOM神经网络没有改变BP神经网络过度依赖网络初始权值阈值的缺陷。黄玮[11]采用SOMBP（Self Organizing Maps Back Propagation）神经网络模型对混合动力汽车进行故障诊断，结果表明SOMBP神经网络在未达到目标精度时停止训练。在BP神经网络初始权值阈值优化方面，粒子群算法（Particle Swarm Optimization，PSO）作为一种基于群体的随机搜索算法[12]，由于具有精度高、收敛速度快等优势被应用于BP神经网络优化。邹兰[13]采用PSO算法对SOMBP神经网络预测模型进行优化，优化后的模型识别率从90%上升至95%。然而，尽管PSO算法优化的模型识别率大幅度提升，但是PSO算法也存在随迭代次数增加网络收敛速度变慢、易陷入局部最优等缺陷[14]。针对PSO优化的问题，黄俊[15]采用一种改进量子粒子群（Improved Quantum Particle Swarm Optimization，IQPSO）算法优化支持向量机（Support Vector Machines，SVM）模型对边坡变形进行预测，试验结果表明，与传统PSO优化后的SVM模型相比，模型的预测误差由4.20降至0.15。

基于以上现状，本文采用SOMBP神经网络模型，针对BP神经网络初始权值阈值优化，采用PSO算法优化BP神经网络。为解决PSO算法收敛速度慢、容易陷入局部最优等缺点对PSO算法进行改进，提出了LWD-QPSO（Linear Weight Decrease-Quantum Particle Swarm Optimization）改进算法。在分析拖拉机柴油机故障机理的基础上，确定了反映故障发生的8种传感器数据信号，最 后 确 定LWD-QPSO-SOMBP（Linear Weight Decrease-Quantum Particle Swarm Optimization-Self Organizing Maps Back Propagation）神经网络模型的结构参数，基于CAN（Controller Area Network）总线技术采集潍柴WP6型拖拉机柴油机5种故障下70组传感器数据对LWD-QPSO-SOMBP神经网络模型的诊断效果进行验证。

1 LWD-QPSO-SOMBP神经网络模型

1.1 SOMBP神经网络

BP神经网络被应用于处理复杂非线性问题[16]，但BP神经网络训练依赖训练样本特征。SOM神经网络是一种无监督学习算法模型[17]，由输入层与竞争层组成，竞争层中神经元输出代表聚类结果[18]。该模型通过数据的聚类和降维实现数据特征提取[19-21]，在降维过程中数据的原特征能够得以保留。因此本文利用SOM神经网络对BP神经网络样本数据进行初步分类，构建SOMBP神经网络模型，以提高BP神经网络性能。

图1为SOMBP神经网络模型图。BP神经网络的训练数据先经SOM神经网络聚类处理，聚类后的标签数据与训练数据组成新的训练数据，BP神经网络根据新的训练数据训练网络。新的训练数据由于拥有SOM神经网络处理后的标签数据，训练数据特征性增强，进而缓解BP神经网络的训练压力。

1.2 LWD-QPSO算法

BP神经网络性能还受到网络初始权值阈值制约，初始权值阈值选取不当会使网络无法找到全局最优值，训练不出合适网络[22]。PSO算法由于具有优良的全局寻优能力被广泛应用于参数寻优[23-24]。本文采用PSO算法优化BP神经网络初始权值阈值。

PSO算法核心步骤有2个，即粒子更新速度计算和粒子位置更新[25]。设种群规模（粒子数）为N；总迭代（进化）次数T；粒子目前迭代次数为t，粒子的目前位置为xt；粒子的目前移动速度为vt。

每个粒子速度更新公式为式中vt+1为更新后的粒子移动速度，ωb为惯性权值，c1为个体学习因子，c2为社会学习因子，r1、r2为2个不相同的[0，1]间随机数，p best为粒子目前的个体最优解，g best为粒子目前的全局最优解。

每个粒子位置更新公式为

式中xt+1为更新后的粒子位置。

PSO算法收敛速度快，但同时也存在易过早收敛、易陷入局部最优等缺点[26-28]，因此需要对PSO算法进行优化。惯性权值递减（Linear Weight Decrease，LWD）通过改变PSO算法在不同时期的搜索能力进而提高粒子寻优的精度；QPSO（Quantum Particle Swarm Optimization）算法能够克服粒子连续变化引起的粒子搜索范围有限的缺陷，使粒子具有更大寻优空间；PSO算法进行迭代运算的后期会出现粒子多样性丧失的现象，自适应变异能够通过几率变异增加PSO算法后期粒子的多样性进而扩大PSO算法后期的寻优空间。

本文综合上述思想对PSO算法进行改进，提出一种LWD-QPSO算法。以QPSO为主体将LWD中随迭代次数改变的惯性权值引入到QPSO位置更新公式，实现算法全局高精度寻优；同时采用一种随迭代次数增加变异几率增大的自适应变异算法对QPSO种群更新方式进行改进，实现对粒子在算法不同时期变异概率的控制，进而使QPSO具有更大的寻优范围，突破QPSO易陷入局部最优的缺陷。

LWD-QPSO算法每个粒子速度更新公式为

式中lω为变量惯性权值，sω为最大惯性权值，eω为最小惯性权值，t/T为粒子目前迭代次数与总迭代次数的比值。

LWD-QPSO算法中每个粒子需要2次位置更新，第1次位置更新公式为

式中u、3r、4r为3个不相同的[0，1]间随机数，pibest为第i个粒子目前的最优解。

第2次位置更新公式为

式中rand(0,t/T)为0～t/T之间的随机数。

1.3 LWD-QPSO-SOMBP神经网络

LWD-QPSO-SOMBP神经网络算法流程如图2。

LWD-QPSO-SOMBP神经网络算法流程具体为：对网络的输入数据进行归一化处理，设置SOM神经网络参数，并根据输入数据对SOM神经网络进行训练，输出聚类结果；对聚类结果进行降维处理，归一化降维后得到一维标签向量，与输入数据组合成为新数据组，以新数据组作为BP神经网络输入；设置BP神经网络的参数，确定SOMBP神经网络的拓扑结构；采用LWD-QPSO算法优化BP神经网络初始权值阈值，以LWD-QPSO速度和位置更新公式更新粒子速度及位置，判断粒子是否符合变异条件，若符合则再次更新粒子位置；以BP神经网络的均方根误差公式计算粒子适应度，根据适应度大小更新粒子群个体极值和群体极值；判断当前是否满足LWD-QPSO算法的终止条件，若为真则将最优的粒子赋值给BP神经网络的权值及阈值，训练赋值后的SOMBP神经网络。

2 拖拉机柴油机故障分析

目前拖拉机柴油机的主要故障形式有柴油机润滑系统故障、怠速不稳、柴油机输出功率不足、排气系统冒黑烟等[29]。上述4种故障形式的典型表征为机油压力低、进气管堵塞、高压油泵故障及活塞环断裂[30-32]。本文以这4种故障表征为基础，分析能够反映拖拉机柴油机故障发生的异常数据信号。

2.1 机油压力低

图3为拖拉机柴油机润滑系统。拖拉机柴油机润滑系统故障是拖拉机运行中常见的现象，其表征之一就是机油压力降低[33]。

如图3所示，配气机构位于拖拉机柴油机润滑系统的末端，润滑状况较其他部位差，机油压力低时机油难以到达配气机构的进、排气凸轮轴，加剧了进、排气凸轮轴与传动部件的碰撞与摩擦，导致其相对位置发生改变，直观体现为进、排气凸轮轴位置出现异常。同时，机油压力低会使机内零部件间的润滑效果变差，零件间的剧烈摩擦会产生大量热量，导致冷却液温度升高。

2.2 进气管堵塞

拖拉机柴油机在怠速工况中常存在怠速不稳的故障，怠速不稳时柴油机常出现抖动、转速不均、易熄火等现象[34]。当进气管发生堵塞时拖拉机柴油机的进气量大幅度降低，直接导致怠速不稳。怠速不稳时发动机的转速会发生大幅度抖动，因此进气管发生堵塞时转速势必发生变化。此外，进气管堵塞时进气量会明显下降，导致进气歧管压力及空气流量发生变化[35]。

2.3 高压油泵故障

高压油泵作为拖拉机柴油机燃油系统的重要部件，其工作情况直接影响拖拉机柴油机的输出功率。高压油泵发生故障时，与高压油泵相连接的供油提前装置运行所需的驱动力中断，供油提前装置无法正常工作，导致供油提前角异常。此外，高压油泵发生故障会使发动机动力不足，柴油机的转速下降[36]。

2.4 活塞环断裂

随着拖拉机使用年限的增加，活塞环易出现磨损及断裂的故障[37]。活塞环断裂时发动机燃烧情况变差，排气系统会出现冒黑烟现象。此时由于机内气缸燃烧室内燃烧情况变差，整机的温度会降低，进而使冷却液温度发生改变。同时，柴油机长时间的不良燃烧会导致发动机抖动，转速也会受到相应影响。

根据上述分析，得出反映拖拉机柴油机故障发生时的异常数据信号，如表1。

表1 拖拉机柴油机故障发生时的异常数据信号Table 1 Abnormal data signal of tractor diesel engine faults

根据表1可知，拖拉机柴油机单个信号无法确定柴油机发生何种故障，某种故障发生会有多种数据信号存在异常。

3 LWD-QPSO-SOMBP神经网络模型性能试验

3.1 试验器材与设备

为检验LWD-QPSO-SOMBP神经网络模型的诊断性能，本文以CAN总线采集拖拉机柴油机运行过程中传感器数据，进行故障诊断试验。试验机型为潍柴WP6型拖拉机柴油机，试验数据采集装置为USBCAN-Ⅱ C，数据解析采用美国汽车工程师协会（Society of Automotive Engineers，SAE）的J1939协议，数据解析软件为CAN Pro，以MATLAB R2018a作为LWD-QPSO-SOMBP神经网络模型的执行软件。

3.2 试验方案

3.2.1 数据采集

试验数据采集装置由CAN总线和USBCAN-Ⅱ C装置构成。如图4为CAN总线，CAN总线将多个拖拉机柴油机电子系统串联起来，其中包含本试验所采用的传感器：转速传感器（型号为M22×1.5，精度为±（20～30） r/min）、转矩转速传感器（型号为JLN-205，精度为±0.1%F.S）、冷却液温度传感器（型号为23 522 855，精度为±0.1 ℃）、空气流量传感器（型号为4 984 760，精度为±1.5%F.S）、进气管压力传感器（型号为A2 C96 053 500，精度为±0.05% F.S）、凸轮轴位置传感器（型号为0 281 002 315，精度为±1.5°）。CAN总线的通讯形式简单，仅由CAN高（CAN-High）数据线和CAN低（CAN-LOW）数据线组成。USBCAN-Ⅱ C装置中有专供CAN-High数据线和CAN-LOW数据线接入的L、H接脚，接线后对USBCAN-Ⅱ C供电，即可完成拖拉机柴油机传感器数据采集。

3.2.2 数据解析

CAN总线以CAN报文为载体传输数据，传感器的数据寄存于CAN报文中，因此需要对CAN报文进行解析，提取传感器数据。本试验采用SAE的J1939协议对CAN报文进行解析[38]。如表2，J1939协议详细定义了CAN报文中的参数信息。

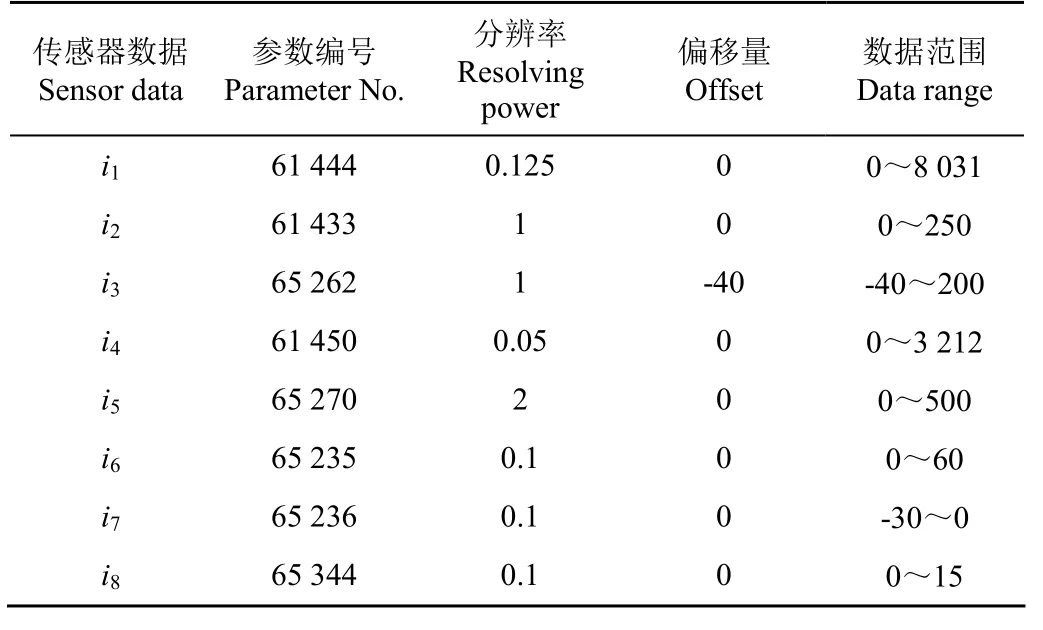
表2 J1939协议参数信息Table 2 J1939 protocol parameter information

提取CAN报文中的参数值，根据公式（6）计算传感器的实际参数值。

式中V为传感器实际参数值，A为CAN报文中的参数值，Rp为分辨率，Of为偏移量。

3.2.3 基于CAN总线的故障诊断试验方案

试验采用南京农业大学工学院自主研制的液压机械无级变速箱（Hydro Mechanical Continuously Variable Transmission，HMCVT）试验台架。如图5所示，该试验台架由潍柴WP6型拖拉机柴油机、液压站、液压机械无级变速箱、传动轴、升速箱及电涡流测功机组成，试验台架设有供各装置传感器数据传输的CAN总线。

CAN总线布置于试验台架内部，直接找出CAN总线中的CAN-High数据线和CAN-LOW数据线是困难的。因此试验采用OBD（On-Board-Diagnose）数据线与试验台架自带的OBD接口将CAN总线中CAN-High数据线和CAN-LOW数据线引出，将二者接入USBCAN-Ⅱ C装置实现数据采集。CAN Pro软件是一款专门用于CAN总线高层协议的分析软件，能够兼容J1939协议，并能够将解析CAN报文得到的传感器数据储存为Excel格式，因此试验采用CAN Pro软件解析数据，将解析后的Excel格式数据导入MATLAB R2018a软件工作目录中，执行LWD-QPSO-SOMBP神经网络模型得出故障诊断结果。

以上述试验方案为基础，采集潍柴WP6型拖拉机柴油机在O1、O2、O3、O4、O5这5种类型故障下的传感器信号数据共70组，每种故障的数据各14组。从70组信号数据中每种故障随机抽取4组数据，共20组数据作为LWD-QPSO-SOMBP神经网络模型测试样本，其余50组作为训练样本。对5种故障的数据设置与其对应的标签，如表3所示。

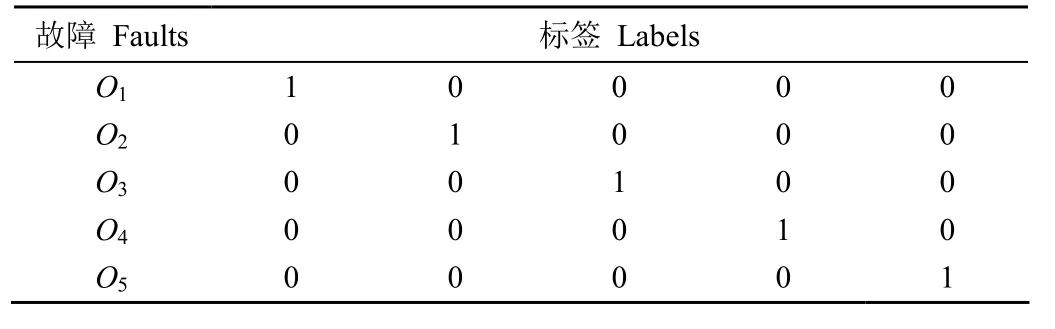
表3 拖拉机柴油机故障标签Table 3 Tractor diesel engine fault label

3.3 LWD-QPSO-SOMBP神经网络模型结构参数确定

根据试验方案，LWD-QPSO-SOMBP神经网络模型的输入维度即为测试样本采集传感器信号种类数目，输出维度为测试样本故障类型数目。LWD-QPSO-SOMBP神经网络需要确定SOM神经网络结构参数和BP神经网络结构参数，其中SOM神经网络中竞争层神经元和BP神经网络中隐含层神经元较难确定，本文详细分析上述2种结构参数。

3.3.1 竞争层神经元

竞争层神经元排列方式有二维平面排列和一维线阵排列2种，二维平面排列竞争层比一维线阵排列竞争层结构复杂。LWD-QPSO-SOMBP神经网络模型仅用SOM神经网络对测试样本做初步分类，因此需要简化SOM神经网络的结构以优化LWD-QPSO-SOMBP神经网络模型，故竞争层的神经元排列方式选取一维线阵排列。

本试验中测试样本的类型数目为5，则要求SOM神经网络能够将测试样本初步分为5类。SOM神经网络采取竞争方式训练网络[39]，为避免SOM神经网络训练过程某个竞争层神经元被“淘汰”无法进行输出，竞争层神经元的个数要大于网络分类数量。对于本文的LWDQPSO-SOMBP神经网络模型，竞争层神经元的个数需大于5。为确定竞争层神经元个数，以50组训练样本训练竞争层神经元数目大于5的SOM神经网络。图6为不同竞争层神经元个数SOM神经网络的分类结果，竞争层神经元输出数据的个数代表SOM神经网络的聚类结果。

由图6可知，竞争层神经元个数为6、7时，SOM神经网络的分类太粗糙，无法将测试样本聚为5类；当竞争层神经元个数为9时，SOM神经网络开始出现过分类现象，分类太细使测试样本无法成功聚类；而当竞争层神经元个数为8时，SOM神经网络可将测试样本聚为5类，故竞争层神经元个数选为8。

3.3.2 隐含层神经元

隐含节点的数h一般由经验公式确定：

式中out为BP神经网络输出层神经元数目，与LWD-QPSO-SOMBP神经网络模型输出维度相同，in为BP神经网络输入层神经元数目，为LWD-QPSO-SOMBP神经网络模型输入维度与SOM神经网络输出标签维度的和，σ为1～10间的整数，a、b、c取为正整数。据此确定隐含层节点的数目取值范围为4～13。

目前的理论没有明确规定隐含层神经元个数取值[40]。为确定隐含层神经元个数，以50组训练样本分别训练具有4～13隐含层神经元数目的BP神经网络，网络训练精度误差如图7。

由图7可知，隐含层神经元数为13时网络训练精度误差最小，故BP神经网络隐含层神经元数选为13。综合上述分析，确定LWD-QPSO-SOMBP神经网络模型的结构参数如表4。

表4 LWD-QPSO-SOMBP神经网络模型结构参数Table 4 Structure parameters of LWD-QPSO-SOMBP neural network model

3.4 试验结果与分析

为验证LWD-QPSO-SOMBP神经网络性能，以50组训练样本进行网络训练。表5为网络误差目标值设为0.001时BP神经网络、SOMBP神经网络、PSO-SOMBP

表5 不同神经网络模型性能Table 5 Performance of different neural network models

（Particle Swarm Optimization-Self Organizing Maps Back Propagation）神经网络、LWD-PSO-SOMBP（Linear Weight Decrease-Particle Swarm Optimization-Self Organizing Maps Back Propagation）神经网络、采用IQPSO优化算法的IQPSO-SOMBP（Improved Quantum Particle Swarm Optimization-Self Organizing Maps Back Propagation）神经网络、LWD-QPSO-SOMBP神经网络模型的性能。

PSO、LWD-PSO、IQPSO、LWD-QPSO4种PSO算法的粒子适应度如图8。

根据表5和图8可知，在神经网络的收敛速度方面，BP神经网络在迭代2 431次时完成网络训练，而SOMBP神经网络仅迭代784次时完成网络训练，验证了SOM神经网络能够减小BP神经网络的训练压力；经过4种PSO优化的SOMBP神经网络迭代不超过500次完成网络训练，其中LWD-QPSO-SOMBP神经网络在迭代63次完成网络训练，网络迭代次数最多下降了97.40%。

在神经网络收敛精度方面，BP神经网络在迭代2 431次时误差达到0.004，此时神经网络未达到训练精度停止训练，SOMBP神经网络、PSO-SOMBP神经网络、LWD-PSO-SOMBP神经网络、IQPSO-SOMBP神经网络虽然加快了收敛速度，但是分别在误差达到0.008、0.004、0.008、0.004时就停止训练，网络误差均没有达到目标值。本文LWD-QPSO-SOMBP神经网络模型训练误差能够下降到0.0006，较单BP神经网络的误差下降了85.00%，达到了目标值。LWD-QPSO算法的粒子适应度最低（0.11），较传统PSO算法粒子适应度（0.15）下降了26.67%。相对IQPSO算法，本文LWD-QPSO算法采用LWD方法更新粒子速度和位置，使粒子全局寻优精度得以提高，算法引入自适应变异，避免了算法后期粒子多样性丧失，进一步增强了粒子的寻优能力。据此可知，LWD-QPSO-SOMBP神经网络模型在网络训练过程中具有良好的性能。

以20组测试样本测试BP、SOMBP、PSO-SOMBP、LWD-PSO-SOMBP、IQPSO-SOMBP和LWD-QPSOSOMBP神经网络诊断效果。选取20组测试样本对应输出的总误差、平均相对误差、均方误差、总准确率以及5种故障的准确率评价网络模型的诊断效果，如表6。

由表6可知，较其他5种模型，LWD-QPSOSOMBP神经网络模型的诊断性能最佳：LWD-QPSOSOMBP神经网络模型的总准确率最高为99.44%，LWD-QPSO-SOMBP神经网络模型输出的总误差为0.111 8、平均相对误差为0.005 8、均方误差为0.000 3，相比其他5种神经网络模型均为最低，这是由于LWD-QPSO-SOMBP神经网络模型通过SOM神经网络的对输入数据进行初步聚类处理，将SOM神经网络的输出标签加入到输入数据可大幅度减小BP神经网络的识别负担，加强BP神经网络识别能力使模型的故障诊断率提升；其次，LWD-QPSO-SOMBP神经网络模型采用LWDQPSO算法优化网络初始权值阈值，充分挖掘PSO的优化潜力，大幅度增强网络的泛化能力。综上，LWDQPSO-SOMBP神经网络模型具有良好的诊断性能。

表6 不同神经网络诊断结果Table 6 Diagnostic results of different neural networks

4 结 论

1）本文针对传统BP神经网络和粒子群算法的缺点，设计了LWD-QPSO-SOMBP神经网络模型；分析了柴油机的故障机理，以此为基础确定8个反映柴油机故障发生的数据信号；通过试验确定了LWD-QPSO-SOMBP神经网络模型的结构参数取值。

2）采用50组潍柴WP6型拖拉机柴油机信号数据作为训练样本对LWD-QPSO-SOMBP神经网络模型及其他5种神经网络模型的性能进行试验。试验表明，LWD-QPSO-SOMBP神经网络模型的网络迭代次数由单BP神经网络的2 431次降为63次，下降了97.40%；训练误差由0.004降为0.000 6，下降了85.00% ；LWD-QPSO算法的粒子适应度由PSO算法的0.15降为0.11，下降了26.67%。

3）采用20组潍柴WP6型拖拉机柴油机信号数据作为测试样本对LWD-QPSO-SOMBP神经网络模型及其他5种神经网络模型的诊断效果进行验证。LWDQPSO-SOMBP神经网络输出总误差为0.111 8、平均相对误差为0.005 8、均方误差为0.000 3，相比于其他5种神经网络均为最低。较单BP神经网络模型，LWD-QPSO-SOMBP神经网络模型的诊断准确率由85.00%提升至99.44%，LWD-QPSO-SOMBP神经网络模型具有良好诊断性能。