欧拉是如何破解巴塞尔问题的?
沐季歌

巴塞尔问题是一个著名的数论问题,由瑞士数学家皮耶特罗·门戈利于1644年提出.这个问题是以数学家莱昂哈德·欧拉的家乡——瑞士的第三大城市巴塞尔命名的.1735年,年仅28岁的欧拉就得到了该问题的解法.
一、巴塞尔问题
巴塞尔问题可以简要地描述为一个求和问题:
仔细观察,你会发现巴塞尔问题其实就是一个幂级数求和问题.这个级数的和大约等于1.644934.欧拉发现它的准确值是詈,并在1735年公布该结果.由于这个问题难倒了许多数学家,所以欧拉在发表该结果后马上就出名了.
二、欧拉的解法
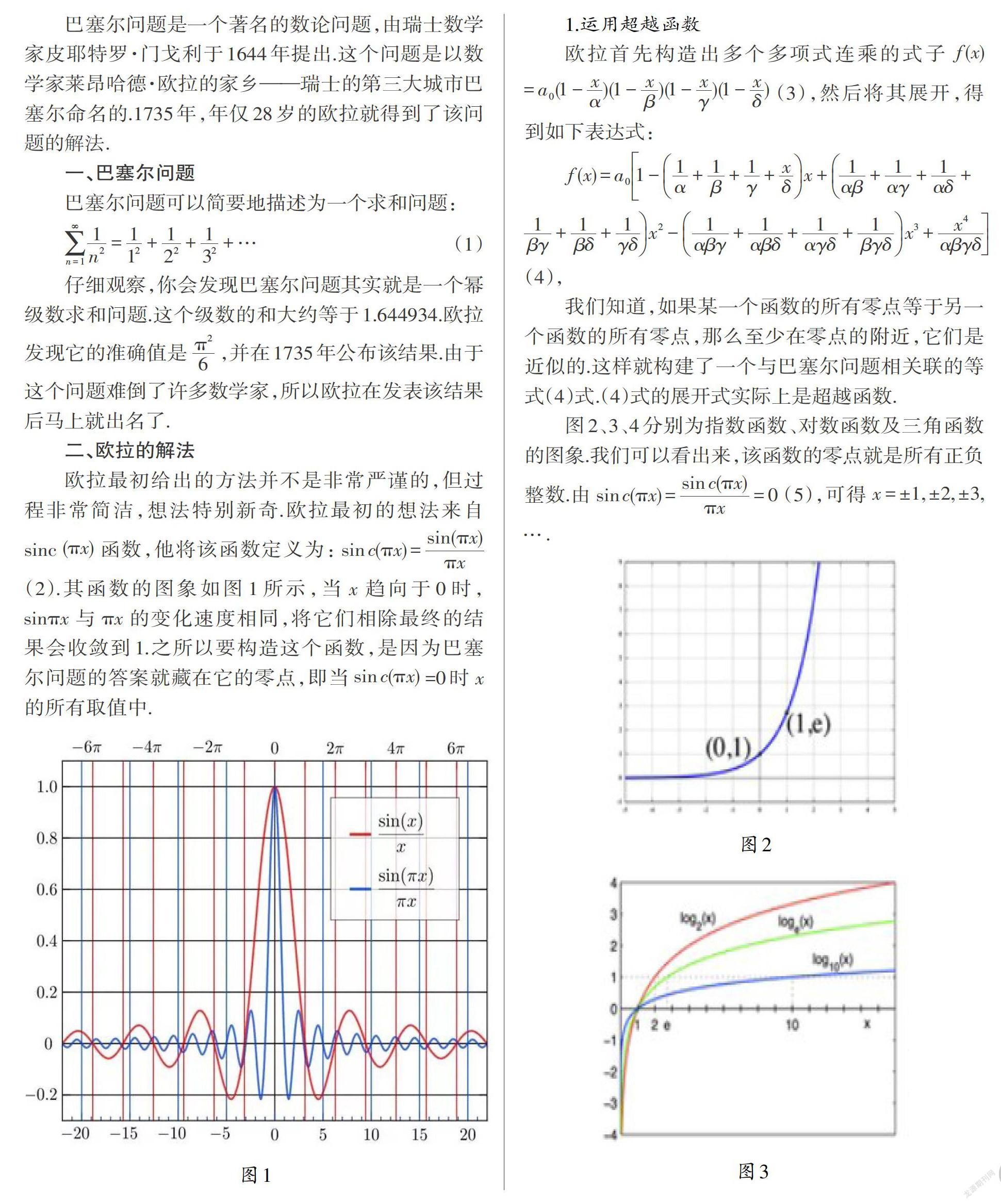
欧拉最初给出的方法并不是非常严谨的,但过程非常简洁,想法特别新奇.欧拉最初的想法来自sinc( X)函数,他将该函数定义为:sinc
(2).其函数的图象如图1所示,当x趋向于0时,
与 X的变化速度相同,将它们相除最终的结果会收敛到1.之所以要构造这个函数,是因为巴塞尔问题的答案就藏在它的零点,即当sinc
=0时x的所有取值中.
1.運用超越函数
欧拉首先构造出多个多项式连乘的式子f(x)
然后将其展开,得到如下表达式:
我们知道,如果某一个函数的所有零点等于另一个函数的所有零点,那么至少在零点的附近,它们是近似的.这样就构建了一个与巴塞尔问题相关联的等式(4)式.(4)式的展开式实际上是超越函数.
图2、3、4分别为指数函数、对数函数及三角函数的图象.我们可以看出来,该函数的零点就是所有正负整数.由
欧拉借助熟悉的式子(1 - x)(l +x)=l- X2来研究
欧拉把这个积式展开,并把所有x的二次项的系数收集在一起,得到x2+…(7).这样,等式右边的式子已经完全展开了,该式中x的二次项的系数为
然后把等
式左边的x移到右边,就会得到一个x的三次项,左边便只剩下
那么只要求出x的三次项的系数的和,便能得出巴塞尔问题的答案.
2.利用泰勒级数
泰勒级数使用了无限项连加的形式来表示某一函数,每一项都是通过求该函数在某一点的n阶导数计算出来的.也就是说,泰勒级数采用了无穷的子项去逼近某一个连续可导函数,每一个高阶导数都是对该值的一点点逼近,最终收敛到该函数.
当项的数目不断增加,泰勒级数最终将收敛于它所表示的函数的极值.图5巾黑色曲线代表sinx(
)函数,其他曲线为其对应不同阶次的泰勒展开式,也就是最高次幂分别为1、3、5、7、9、11和13的多项式.这就需要找到逼近
中x的三次项的系数,图5巾
的7个泰勒展开式为:
f(x)=x,
(7)式的左边可以根据泰勒展开式表示为:
(9).欧拉抽取x2项的系数,将式8看作具有无穷次幂的“伪多项式”,这样的伪多项式有无穷多个根,其对应的根由式(5)给出.通过联立(7)式和(9)式,便可求
展开后的x的
二次项系数的和,即可得到巴塞尔问题的答案:.l+
不仅如此,欧拉在解答巴塞尔问题的过程巾得…了著名的瓦里斯(Wallis)乘积公式,仅需将 代入(6)式并求其倒数即可得到:,
欧拉在解决巴塞尔问题的过程巾并未涉及复杂的技巧与数学概念,只是巧妙地利用超越函数和泰勒级数逐步推导并进行一系列巧妙的变换,便解决了著名的世界数学难题.这样的思考过程、逻辑推理过程,让人惊叹不已.

