DIFFERENTIAL MIXED EQUILIBRIUM PROBLEMS IN BANACH SPACE
WANG Zhi-wei,JU Gui-yin
(School of Applied Mathematics,Nanjing University of Finance and Economics,Nanjing 210023,China)
Abstract:In this paper,we investigate a new class of differential mixed equilibrium problems((DME),for short)in Banach space.By using Fan-KKM theorem and Ky Fan’s minmax inequality,we respectively prove the existence of solutions for mixed equilibrium problems under some suitable conditions.Moreover,we prove the superpositional measurability and upper semicontinuity for a class of set-valued mappings.Finally,by using the theory of semigroups and Filippov implicit function lemma,we obtain the existence theorem concerned with the mild solutions for(DME)and discuss the compactness of the solution set.The results enrich and extend the theory of equilibrium.
Keywords:differential mixed equilibrium problems;Banach space;Fan-KKM theorem;Ky Fan’s minmax inequality;Filippov implicit function lemma
1 Introduction and Preliminaries
It was well known that Pang and Stewart introduced and studied differential variational inequality in a finite-dimensional Euclidean space(see[1]).Recently,the existence of solutions for different types of differential variational inequalities problems(see[2-7])is considered by many authors.
In this paper,we introduce a class of differential mixed equilibrium problem.Under various conditions,we obtain the existence theorem concerned with the mild solutions for this class of problems.
Now we introduce some preliminaries which will be used in the paper.For any nonempty set Y,P(Y)denotes the family of all nonempty subsets of Y.We denote
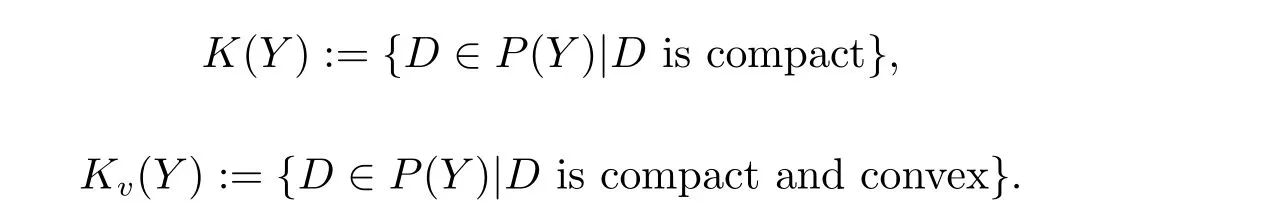


2 The Introduction of Some New Problems

3 Existence and Properties of Solution Sets for Mixed Equilibrium Problems




4 Continuity and Superpositional Measurability for a Class of Set-Valued Mappings

5 Existence of Mild Solutions for a Class of Differential Mixed Equilibrium Problems



Therefore,FixΓ is bounded in C([0,T];E).
Applying Lemma 5.2 and Lemma 1.7 with F=Γ,we know the solution set of problem(EDI),which equals to FixΓ,is compact in C([0,T];E).
Step 3 Note that the set-valued mapping U is superpositionally measurable from Theorem 4.1.Therefore,by Filippov implicit function lemma(see[11]),we deduce that for every solution x of(EDI),there exists a measurable selection u(t)∈U(t,x(t))such that ˙x(t)=Ax(t)+f(t,x(t),u(t)),t∈[0,T].Hence,(x,u)is a mild solution of problem(DME)in the sense of Definition 2.1,which implies the set of all mild trajectories of problem(DME)is consistent with the solution set of problem(EDI).This completes the proof.
- 数学杂志的其它文章
- SHARP ERROR ESTIMATE OF BDF2 SCHEME WITH VARIABLE TIME STEPS FOR LINEAR REACTION-DIFFUSION EQUATIONS
- APPROXIMATIONS OF THE IDENTITY ADAPTED TO CONTINUOUS ELLIPSOID COVER
- THE REPRESENTATION CATEGORIES OF DIAGONAL CROSSED PRODUCTS OF INFINITE-DIMENSIONAL COFROBENIUS HOPF ALGEBRAS
- AN OPTIMAL DIVIDEND STRATEGY IN THE DISCRETE MODEL WHEN PAYMENTS ARE SUBJECT TO BOTH TRANSACTION COSTS AND TAXES
- 阿贝尔方程的两个周期解的存在性
- 一类非线性随机微分方程的统计性质

