基于AFI混合聚类算法的轴承故障诊断方法*

金 阳，王 林，崔朗福，黄云涛，张庆振，张 如，韩晓萱，张超祺，宋子雄

(1.北京航空航天大学 自动化科学与电气工程学院·北京·100191；2.北京航天控制仪器研究所·北京·100854；3.北京航天自动控制研究所·北京·100085)

0 引 言

滚动轴承既是支撑数控机床主轴作回转运动的重要元件，又是精密机床设备的薄弱环节[1]。因此，开展针对滚动轴承故障诊断的研究，对提高设备的可靠性而言具有重要意义。

在基于轴承振动信号分析的故障诊断模型中，两大关键问题是故障特征提取和故障模式识别[2-3]。故障特征提取的主要方法包括基于时域、频域和时频域等的信号处理方法[4-5]。文献[6]提取了信号时域的波形长度(Waveform Length，WL)、Willison幅值(Wilson Amplitude，WAMP)、过零点(Zero Crossing，ZC)和斜率符号改变(Slope Sign Changes，SSC)特征，构成了特征向量，但该方法在强环境噪声的工程实际应用中效果欠佳。文献[7-9]出于对轴承运行时损伤点与正常表面接触时所产生的周期性冲击力的考虑，提取了故障特征频率的相关信息作为特征向量，但此类方法会受轴承制造装配误差以及转速不稳定因素的影响，使实际故障特征频率产生偏移。针对上述问题，本文采用了基于小波包能量特征[10]的提取方法，利用主成分分析方法进一步去除了环境噪声和装配误差等随机成分，完成了对滚动轴承故障模式特征的提取。

人工智能是故障诊断领域发展的重点方向，由于轴承故障的模式多样，故障模式与特征的联系具有不确定、非线性的特点，故障模式的识别方法主要为机器学习方法。文献[11]利用神经网络极强的非线性函数拟合能力实现了轴承故障模式识别；文献[12]利用深度神经网络端到端的学习方式同时实现了信号特征的自学习，但此类方法存在网络模型难以确定、可解释性差、易陷入局部极值以及训练所需样本量维数爆炸等缺点。尤其，对于采用端到端学习方式的神经网络，为完成从原始数据到中间层“隐藏特征”映射的拟合，需要更多的样本；文献[13-15]基于不同的特征提取方法构建了支持向量机的模型，并实现了故障模式识别。该方法对训练样本的需求量相对较小，解释度更高，且不易过拟合。但是，以支持向量机为代表的此类方法仍属于监督式学习方法，需要对样本进行完全标记。在机床轴承振动信号的故障诊断工程实际应用中，对机床设备进行监测得到的是大量未标记数据，通过可接受的工作量的人为标记只可获得小样本量的标记数据。因此，诸如聚类的无监督或半监督的学习式模式识别方法，在工程实际场景下更具优势。此外，任务同时希望诊断模型具备对未知故障模式进行挖掘的能力，即要求采用聚类方法时，不直接指定聚类簇数。针对上述问题，本文提出了一种融合人工鱼群算法、模糊C均值算法和迭代自组织数据分析算法思想的AFI混合聚类算法，并基于此完成了轴承故障诊断模型中的故障模式识别。

1 小波包增强能量特征提取

小波包分解是一种对小波分解进行进一步优化的信号时频分析方法[16]。平方可积空间内的信号s(t)，在小波函数ψ下的连续小波变换计算式如式(1)所示，离散小波变换的计算式如式(2)所示

(1)

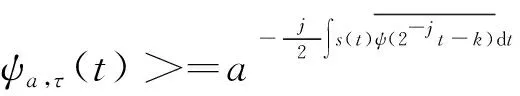
(2)

式中，“< >”表示内积运算，a和τ分别为小波函数ψ的缩放和平移因子，j为小波变换的尺度参数。

(3)

(4)

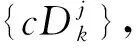
图1 小波包多层次分解示意图Fig.1 Schematic diagram of wavelet packet multi-level decomposition

对长度为N的振动信号序列x(n)进行j层小波包分解，可得到2j个子频带。定义由左至右的第k个子频带的能量E(j,k)如式(5)所示，归一化2j个子频带能量所构成的能量特征向量如式(6)所示

(5)

Hj=[h(j,1),…,h(j,k),…,h(j,2j)]

(6)

由于能量特征向量中存在随机噪声，且高维数据会带来维数灾难，因此对能量特征向量可进一步采用主成分分析方法以增强其特征。首先对数据集X进行Z-score标准化处理，然后计算样本的相关矩阵R如下

(7)

求样本相关矩阵R的m个特征值λi及对应特征值的单位特征向量αi，记特征值从大到小依次为λ1≥λ2≥…≥λm。若根据累计贡献率v决定选取前l个主成分，则这l个主成分为

(8)

记前l个特征值对应的单位特征向量构成矩阵A=[α1,α2,…,αl]m×l，则由主成分分析得到的l个主成分yi构成的k维列向量为

y=ATx

(9)

2 AFI混合聚类算法

2.1 目标函数

AFI混合聚类算法的目标函数采用模糊C均值聚类算法定义的目标函数倒换式形式。相较于K均值等算法，模糊C均值算法融合了模糊集合思想，是一种无监督软聚类方法[18]。方法如下

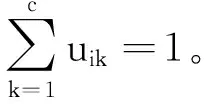
模糊C均值算法的目标函数为

(10)

式中，m∈(1,∞)是模糊指数，用于控制隶属度矩阵的模糊程度。

由Lagrange乘数法求得的隶属度uij和类簇中心vj的迭代式分别为

(11)

(12)

由模糊C均值算法的目标函数Jm，构造AFI混合聚类算法的目标函数为

(13)

目标函数f的值越大，Jm越小，对应更优的聚类结果。其中，k0为一个正数，不妨取k0=1。

2.2 改进的人工鱼群算法

改进的人工鱼群算法引入了迭代自组织数据分析(Iterative Self-organizing Data Analysis，ISODATA)算法的分裂、合并思想，为个体鱼设计了“分裂进化”和“合并进化”两种进化行为。

基本人工鱼群算法通过模拟鱼群个体觅食、聚群、追尾、随机等行为搜寻问题的全局最优解[19]。设初始聚类中心的个数为c，每个样本对象的维度为s，则个体人工鱼Xi的位置矢量可以编码为c×s的矩阵形式

(14)

基本人工鱼群算法中的个体鱼具有如下行为：

(1)觅食行为。设人工鱼当前所处的位置为Xi，在其视野范围内随机选择一个新位置Xj。如果Xj处的食物浓度大于Xi处的食物浓度，则向该方向以随机步长移动一步，否则重新选择新位置。在尝试次数达到上限次数后，转而执行随机游动行为。

(2)聚群行为。设人工鱼当前所处的位置为Xi，在其视野范围内共有nf条伙伴个体鱼，这些伙伴个体鱼的中心位置为Xc。如果Xc处的食物浓度在除以nf后大于Xi处的食物浓度与一个拥挤度因子δ的乘积，则向该方向以随机步长移动一步；否则转而执行觅食行为。

(3)追尾行为。设人工鱼当前所处的位置为Xi，在其视野范围内共有nf条伙伴个体鱼，这些伙伴个体鱼所处的位置中食物浓度最大者为Xj。如果Xj处的食物浓度除以nf后大于Xi处的食物浓度与一个拥挤度因子δ的乘积，则向该方向以随机步长移动一步；否则转而执行觅食行为。

(4)随机游动行为。设人工鱼当前所处的位置为Xi，在其视野范围内随机选择一个新位置Xj，并移动至该位置。

在基本人工鱼群算法中，每条个体鱼在每次移动前均试探执行聚群行为和追尾行为，选择移动后食物浓度值大者为实际执行的行动；每轮所有个体鱼行动完毕后，由公告板记录全部个体鱼中食物浓度最大者的位置Xbest以及相应的食物浓度fbest；重复上述步骤直至满足终止条件，Xbest即为搜寻得到的全局最优解。

ISODATA算法是一种可根据当前迭代情况动态调节类簇数量的聚类算法，其核心思想是在K均值算法的迭代过程中增加“分裂”和“合并”两个操作[20]。该算法不再直接指定固定的聚类簇数，转而指定划分类簇的相关指导参数。参考ISODATA算法的分裂、合并操作，可定义个体鱼的“分裂进化”和“合并进化”两种进化行为：

(1)分裂进化。根据公告板记录的最优个体人工鱼位置，将全部样本划分到当前的k个类簇中。当满足以下情形之一时，即可进行鱼群维度分裂进化

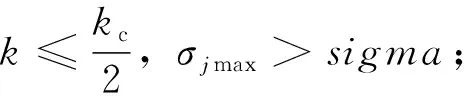
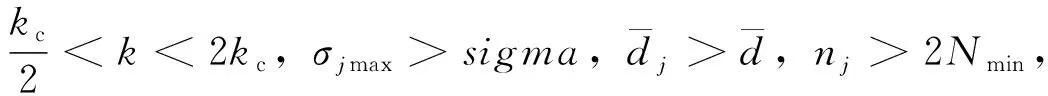
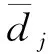
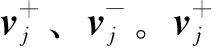
(2)合并进化。根据公告板记录的最优个体人工鱼的位置，将全部样本划分到当前类簇数k的各类簇中。当满足以下情形之一时，即可进行鱼群维度的合并进化：

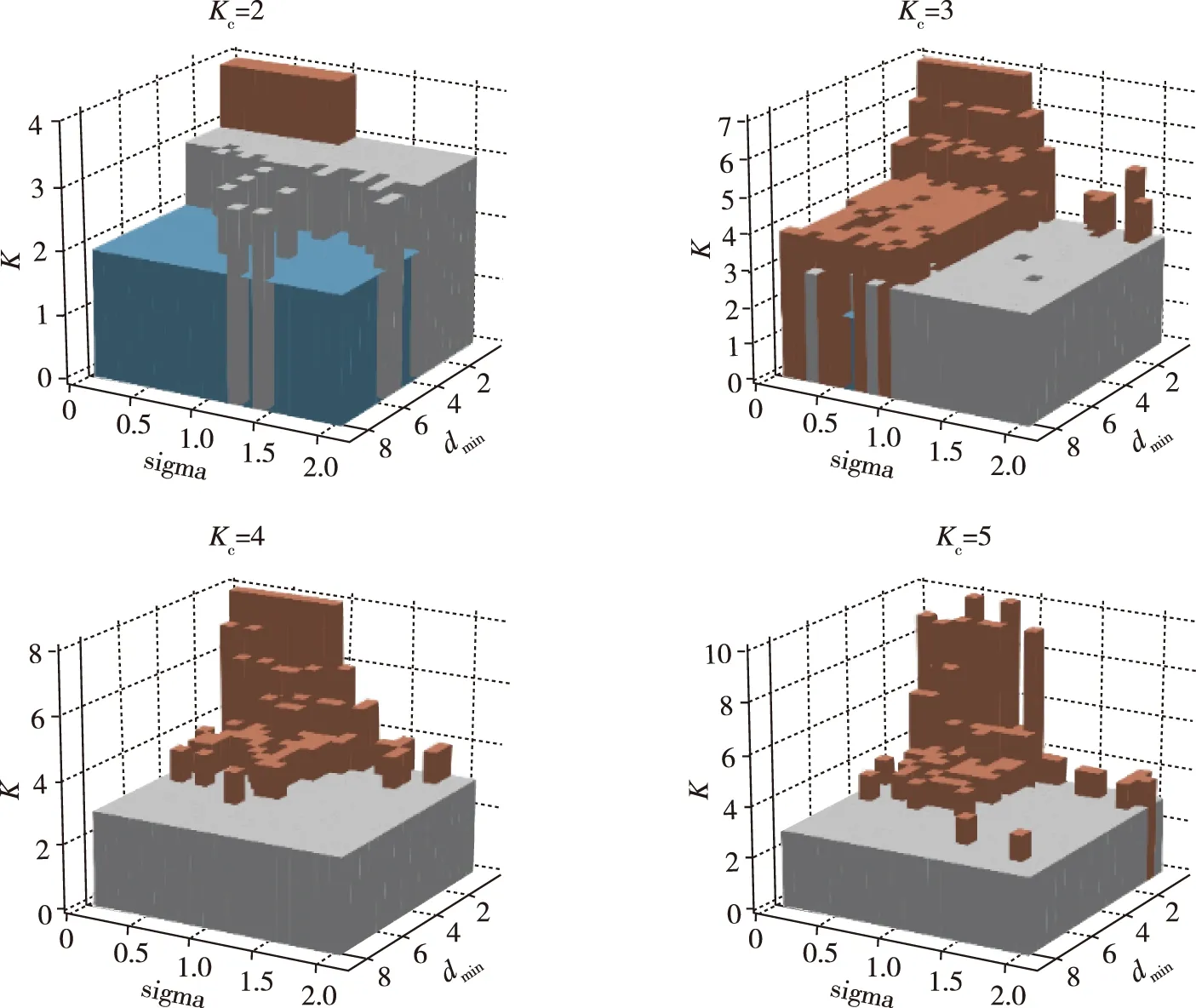
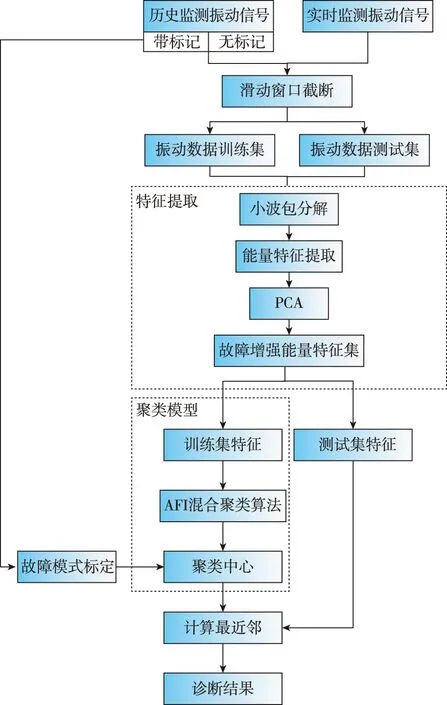
①k≥2kc，Dij

其中，k是当前迭代的类簇数，kc是参考指导类簇数，Dij是最小的两个类簇中心之间的距离，dmin是类簇间最小距离的下限阈值。

需要注意的是，每当“分裂”、“合并”操作发生时，目标函数f的定义域维度随之发生了变化。

2.3 算法描述

AFI混合聚类算法的步骤如下：

(1)设置参数：设置人工鱼群的规模为N，拥挤度因子为δ，人工鱼移动步长为Lstep，视野半径为rvisual，最大试探次数为ntry_number；参考指导类簇数为kc，初始聚类簇数不妨取k0=kc，类簇最小样本数为Nmin，类间最小距离下限阈值为dmin，类内各属性分量分布标准差上限阈值为sigma；模糊指数为m。

(2)初始化：根据式(14)，对N条人工鱼进行编码，随机初始化位置矩阵Xi并计算相应的函数值fi；据此更新公告板的最优函数值及对应人工鱼的位置矩阵；初始化当前维度为N×k0的隶属度矩阵及其他参数。

(3)执行行为：每条人工鱼试探执行聚群行为和追尾行为，选择行动后食物浓度大者为实际执行的行动，更新人工鱼食物浓度fi、隶属度矩阵及其他中间量。

(4)更新公告板：记鱼群中个体食物浓度最大值为fbest，以及对应的人工鱼个体位置矩阵为Xbest。

(5)维度进化：鱼群选择进行维度的分裂进化、合并进化或是保持，进化后更新人工鱼食物浓度fi，重构具有新维度的隶属度矩阵及其他中间量，并进行更新。

(6)更新公告板：记鱼群中个体食物浓度最大值为fbest，以及对应的人工鱼个体位置矩阵为Xbest。

(7)循环及结束：重复步骤(3)～(6)直至满足终止条件；输出公告板中的Xbest及fbest即为全局最优解及对应的函数值。其中，Xbest的矩阵行数即是自动确定的类别数，每个行向量即是各类簇的中心。

图2 AFI混合聚类算法的流程图Fig.2 AFI hybrid clustering algorithm flow chart

3 仿真试验及结果分析

3.1 AFI算法仿真分析

为分析本文所提出的AFI算法的聚类性能，应用该算法对包含3个簇、60个样本的二维数据集进行聚类分析，并将分析结果与采用K均值算法的实验结果对比。聚类过程的误差平方和(Sum of Squared Error，SSE)收敛曲线和聚类结果如图3和图4所示。

图3 AFI算法与K均值算法的SSE收敛曲线Fig.3 SSE convergence curve of AFI algorithm and K-means algorithm

图3和图4表明，K均值算法易受到初值选择的影响，尽管其有可能收敛到全局最小值而得到正确聚类结果(见图3和图4中的“全局最小值情形”)，但也有可能因陷入局部极值而无法得到正确的聚类结果(见图3和图4中的“局部极值情形1”、“局部极值情形2”、“局部极值情形3”)；AFI算法虽然收敛速度慢，但能在可接受的迭代次数内收敛至全局最小值(见图3中的“全局最小值情形(AFI)”标识曲线和图4中的“全局最小值情形”)；值得注意的是，本例采用AFI算法的SSE收敛曲线从第5次迭代周期的158.647指标值，上升至第6次迭代周期的166.252指标值，这一现象由算法自适应调整聚类簇数而导致，在此期间内，对应地将聚类簇数由4类自调整为了3类。

聚类结果的纯度(Purity)、归一化互信息(Normalized Mutual Information，NMI)、调整兰德系数(Adjusted Rand Index，ARI)、误差平方和(Sum of Squared Error，SSE)与准确率(Accuracy)的评价指标值如表1所示。表1进一步说明，K均值算法存在容易陷入局部极值的缺点；AFI算法能够跳出局部极值，得到正确的聚类结果。

表1 AFI算法与K均值算法的聚类结果评价指标

其中，K均值算法采用欧式距离，类簇数k=3；AFI算法采用欧式距离，参数设置如表2所示。

本文所提算法具有动态调节类簇数量的能力，其自动确定最终聚类簇数的性能主要由原ISODATA算法中的相关参数组决定。

图5所示的是采用本文所提AFI算法、使用欧氏距离作为距离度量，设置参考指导类簇数kc依次为2,3,4,5，所确定的类簇数随类内属性分量标准差上限阈值sigma、类间最小距离下限阈值dmin的不同而得到的结果。除kc、sigma、dmin外，其余的参数设置如表2所示。

表2 AFI算法的设置参数值

图5 不同参数下AFI算法第50次迭代自确定的类簇数Fig.5 Self determined number of clusters in the 50th iteration of AFI algorithm with different parameters

图5表明，本文所提AFI算法具有自确定类簇数的能力，其自动确定最终聚类簇数的性能主要由原ISODATA算法中的相关参数组决定。

图6所示是迭代过程中算法自确定的类簇数。实验采用AFI算法，使用欧氏距离作为距离度量，设置参考指导类簇数kc依次为2,3,…,7，除kc外的其余参数设置如表2所示，6次聚类结果均收敛至全局最小值。

图6表明，本文所提AFI算法具有自确定类簇数的能力，且最终确定的类簇数在合理设置其他参数的前提下，在一定范围内对参数“参考指导类簇数kc”不敏感，即不依赖于参考指导类簇数kc的设置。

图6 AFI算法在不同参考指导类簇数下迭代自确定的类簇数Fig.6 AFI algorithm is not sensitive to the number of reference clusters

3.2 故障诊断方法实例分析

本文提出的轴承故障诊断方法的流程如图7所示，其基本步骤如下：

图7 故障诊断流程图Fig.7 Fault diagnosis flow chart

(1)利用滑动窗口对原始振动信号序列做截断操作，得到等长的片段化序列样本；根据部分原始信号所带的标记，为对应样本添加标签。

(2)利用小波包分解、能量特征提取和主成分分析方法，提取得到故障增强能量特征集。

(3)采用AFI混合聚类算法，得到特征空间中代表轴承各故障模式的类簇，进而可得到类簇数和各类簇的中心。

(4)根据各类簇中的带标记样本，由多数投票规则对该类簇的中心进行故障模式标定。

(5)计算测试样本在特征空间内的类簇中心最近邻，并最终将其诊断为该中心所在类簇的故障模式。

为验证本文所提出的基于小波包和AFI混合聚类算法的轴承故障诊断方法的有效性，使用该诊断方法对美国凯斯西储大学提供的故障轴承振动数据集[21]进行诊断实例分析，并将分析结果与采用K均值算法模型的诊断结果进行对比。

数据集采集实验平台如图8所示。使用电火花加工技术分别在内滚道、滚动球体和外滚道引入直径为3.556×10-4m的缺陷造成单点故障，将故障轴承安装到实验电机中，电机负载为745.77W，电机转速为1772r/min。在电机的驱动端安装加速度传感器采集实验数据，设置采样频率为12kHz。

图8 滚动轴承模拟故障实验平台[22]Fig.8 Rolling bearing fault simulation platform[22]

采用滑动窗口将三种故障模式的原始振动信号序列分割为长度为2048(时间窗宽为0.1707s)的片段化信号样本集。从样本集的每种故障模式中选取65个样本，将其中50个样本用于训练构建诊断模型，其余15个样本用于测试模型诊断效果。样本集矩阵为X195×2048=[x1,x2,…,x195]T，其中的3个示例样本如图9所示，样本编号如表3所示。

(a)

(b)图9 不同故障模式的轴承振动信号时序图(a)和幅频谱图(b)Fig.9 Vibration sequence diagram (a) and amplitude spectrum (b) of bearings with different fault modes

表3 不同故障模式的样本

表4 各主成分贡献率及累计主成分贡献率

采用基于AFI混合聚类算法和基于K均值聚类算法的两种方法分别独立地进行10次随机实验。AFI算法采用欧式距离，其参数设置如表5所示；K均值算法采用欧式距离，给定的先验类簇数为3。

表5 AFI算法的设置参数值

图10所示是采用AFI混合聚类算法在第3次实验时的增强能量特征空间中代表轴承各故障模式的类簇及类簇中心，算法自确定的类簇数为3，根据多数投票规则对类簇所属的故障模式进行了标定；图11所示的是采用K均值聚类算法在第2次实验(收敛于局部极值)时的增强能量特征空间中代表轴承各故障模式的类簇及类簇中心，类簇数量3作为先验条件由人为指定，根据带标记样本的标签与多数投票规则也可对类簇所属的故障模式进行标定。

图10 采用AFI算法时样本在特征空间中的分布Fig.10 The distribution of samples in the feature space using the AFI algorithm

图11 采用K均值算法时样本在特征空间中的分布Fig.11 The distribution of samples in the feature space using the K-means algorithm

表6记录了10次随机实验的聚类结果评价指标。由表6可以看出，在机床轴承振动信号的故障诊断模型中，复杂的数据使K均值算法中的50%的频率陷入了局部极值，而AFI算法能够避免频率陷入局部极值，进而得到准确的聚类结果。

表6 10次随机实验的聚类结果评价指标

表7记录了当采用两种算法分别进行10次随机实验时，所建立的诊断模型在测试特征集上的诊断准确率。结果表明，本文所提出的基于AFI混合聚类算法的轴承故障诊断方法，相比基于K均值算法的方法，具有更高的故障模式识别准确率。

表7 两种诊断模型在测试特征集上的诊断准确率

4 结 论

本文提出了一种基于AFI混合聚类算法的滚动轴承故障诊断方法，本方法具有如下优点：(1)方法基于无监督式学习的AFI混合聚类算法，与基于神经网络、支持向量机等的方法相比，能够在标记样本量小的前提下完成训练，实现有效诊断；(2)方法基于能够避免陷入局部极值的AFI混合聚类算法，与基于K均值等的同类方法相比，故障模式识别的准确率更高，诊断性能更优；(3)方法基于在合理参数下具有动态自调节并确定聚类簇数能力的AFI混合聚类算法，与基于K均值、模糊C均值等的同类方法相比，解决了分析给定样本划分类簇数而先验知识不足的问题，在未知故障模式的挖掘领域中也具有应用前景。本文所提方法中的AFI算法因构建于群体智能算法和迭代自组织数据分析算法之上，收敛速度较慢，故有待进一步优化和完善。

参考文献(References)

[1] WANG R, ZHANG Z, XIA Z, et al. A new approach for rolling bearing fault diagnosis based on EEMD hierarchical entropy and improved CS-SVM[C]// 2019 Prognostics and System Health Management Conference (PHM-Qingdao). Qingdao, China: IEEE, 2019: 1-6.

[2] PURASHOTHAM V, NARAYANAN S, PRASAD S. Multi-fault diagnosis of rolling bearing elements using wavelet analysis and hidden Markov model based fault recognition[J]. NDT & E International, 2005, 38(8):654-664.

[3] CHANG Y, BAO G, CHENG S, et al. Improved VMD-KFCM algorithm for the fault diagnosis of rolling bearing vibration signals[J]. IET Signal Processing, 2021, 15(7): 238-250.

[4] 王奉涛, 苏文胜. 滚动轴承故障诊断与寿命预测[M]. 北京: 科学出版社, 2018: 59-65.

WANG F T, SU W S. Fault diagnosis and life prediction of rolling bearings[M]. Beijing: Science Press, 2018: 59-65. (in Chinese)

[5] 王悦斌, 张建秋. 时频信号的非参数加窗稀疏协方差迭代分析法[J]. 飞控与探测, 2019, 2(1): 24-31.

WANG Y B, ZHANG J Q. A nonparametric windowed sparse iterative covariance-based estimation approach to time-frequency signals[J]. Flight Control & Detection, 2019, 2(1): 24-31(in Chinese).

[6] NAYANA B R, GEETHANJALI P. Analysis of statistical time-domain features effectiveness in identification of bearing faults from vibration signal[J]. IEEE Sensors Journal, 2017, 17(99): 5618-5625.

[7] GEBRAEEL N, LAWLEY M, LIU R, et al. Residual life predictions from vibration-based degradation signals: a neural network approach[J]. IEEE Transactions on Industrial Electronics, 2004, 51(3): 694-700.

[8] BOZCHALOOI I S, LIANG M. A joint resonance frequency estimation and in-band noise reduction method for enhancing the detectability of bearing fault signals[J]. Mechanical Systems & Signal Processing, 2008, 22(4): 915-933.

[9] ARUN P, LINCON S A, PRABHAKARAN N. Detection and characterization of bearing faults from the frequency domain features of vibration[J]. IETE Journal of Research, 2018, 64(5): 634-647.

[10] YEN G G, LIN K C. Wavelet packet feature extraction for vibration monitoring[J]. IEEE Transactions on Industrial Electronics, 2000, 47(3): 650-667.

[11] FANG S, WEI Z J. Rolling bearing fault diagnosis based on wavelet packet and RBF neural network[C]// Control Conference. Zhangjiajie, China: IEEE, 2007: 451-455.

[12] XIE J Q, DU G F, SHEN C Q, et al. An end-to-end model based on improved adaptive deep belief network and its application to bearing fault diagnosis[J]. IEEE Access, 2018, 6: 63584-63596.

[13] CHEN R Y, HUANG D R, ZHAO L. Fault diagnosis of rolling bearing based on EEMD information entropy and improved SVM[C]// 2019 Chinese Control Conference (CCC). Guangzhou, China: IEEE, 2019: 4961-4966.

[14] NIKRAVESH Y, REZAIE H, KILPATRIK M, et al. Intelligent fault diagnosis of bearings based on energy levels in frequency bands using wavelet and support vector machines (SVM)[J]. Journal of Manufacturing & Materials Processing, 2019, 3(1): 11.

[15] WENG P Y, LIU M K. Roller bearing fault diagnosis based on wavelet packet decomposition and support vector machine[C]// 2017 International Conference on Applied System Innovation(ICASI). Sapporo, Japan: IEEE, 2017: 33-36.

[16] COIFMAN R R, MEYER Y, QUAKE S, et al. Signal processing and compression with wavelet packets[M]. Dordrecht: Springer, 1994: 363-379.

[17] MALLAT S. A theory for multiresolution signal decomposition: the wavelet representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(7):674-693.

[18] BEZDEK J C, EHRLICH R, FULL W. FCM: the fuzzy C-means clustering algorithm[J]. Computers & Geosciences, 1984, 10(2-3): 191-203.

[19] 李晓磊, 邵之江, 钱积新. 一种基于动物自治体的寻优模式:鱼群算法[J]. 系统工程理论与实践, 2002, 12(11): 32-38.

LI X L, SHAO Z J, QIAN J X.An optimization model based on animal autonomy: fish swarm algorithm[J]. System Engineering Theory And Practice, 2002, 12(11): 32-38(in Chinese).

[20] BALL G H, HALL D J. ISODATA, a novel method of data analysis and pattern classification[M]. California: Technical Rept, 1965.

[21] CENTER B D. Case Western reserve university bearing failure data set[DB/OL]. (2011-12-10][2021-02-20]. https://csegroups.case.edu/bearingdatacenter/pages/12k-drive-end-bearing-fault-data.

[22] CENTER B D. Bearing fault simulation experiment platform of Case Western Reserve University[EB/OL]. (2011-12-10][2021-02-20] https://csegroups.case.edu/bearingdatacenter/pages/apparatus-procedures.