含Cu硫化物中S、Fe同位素分馏系数的第一性原理计算

刘善琪，梁家新，张秋院，李永兵

(1. 中山大学 地球科学与工程学院， 广东 广州 510275； 2. 南方海洋科学与工程广东省实验室(珠海)， 广东 珠海519080； 3. 中国科学院大学 地球与行星科学学院， 北京 100049； 4. 中国科学院计算地球动力学重点实验室， 北京 100049)

Cu在自然界主要以硫化物的形式存在，全球Cu储量的近90%来自硫化物，如黄铜矿、斑铜矿和辉铜矿(Kabata-Pendias and Szteke， 2015； Ober, 2016)。确定硫化物的基本性质尤其是同位素分馏性质是了解铜矿床形成的条件及过程的关键，反之又可以为勘探此类矿床及其后续开采提供依据(Vaughan， 2006)。

利用硫化物中的S同位素分馏来示踪成矿作用过程和成矿物质来源已有很长的历史，但是由于S同位素分馏系数的缺乏以及不同方法确定的分馏系数的差异较大，使得S同位素并不能很好地发挥其示踪作用(Seal， 2006； Marinietal., 2011)。迄今为止只有为数不多的几种含Cu硫化物的S同位素分馏系数得到了确定：Li等(2006)采用改进的增量方法确定了黄铜矿、斑铜矿和方黄铜矿的S同位素分馏系数；Polyakov等(2011)利用黄铜矿中Cu和S的声子态密度计算了黄铜矿的S同位素分馏系数。但是这两种方法确定的S同位素分馏系数有很大差别。大部分含Cu硫化物的S同位素分馏系数有待进一步确定。

近年，斑岩铜矿中硫化物的Fe同位素分馏研究取得了一定进展(Grahametal., 2004； Wangetal., 2018； Heetal., 2020；Tangetal., 2020)。随着MC-ICP-MS测试技术的发展，Fe同位素已被用于探究生物地球化学、热液流体演化、太阳系演化和行星分异等多种自然过程(Dauphasetal., 2017)。所有这些应用都取决于含铁物质Fe同位素分馏系数的确定。斑岩铜矿中含Fe和Cu的矿物主要有黄铜矿、斑铜矿和方黄铜矿(Bergeretal., 2008)。尤其是斑铜矿，具有随温度变化的3种同质多像体(Makovicky， 2006)，根据之前的研究可以基本推断这3种同质多像体的Fe同位素分馏性质是不同的(Liuetal., 2018)。据文献记载，只有黄铜矿的Fe同位素分馏系数得到了计算研究(Polyakov and Soultanov, 2011； Dauphasetal., 2012)，但不同学者的计算结果却有很大的差异。

本文采用基于密度泛函微扰理论的第一性原理计算确定主要含Cu硫化物，包括黄铜矿(CuFeS2)、斑铜矿(Cu5FeS4)、方黄铜矿(CuFe2S3)、辉铜矿(Cu2S)、铜蓝(CuS)、黑硫铜镍矿(CuS2)在0～1 000℃之间的S同位素简约配分函数比(103lnβ34-33)，以及Cu-Fe硫化物黄铜矿、斑铜矿和方黄铜矿在0～1 000℃之间的Fe同位素简约配分函数比(103lnβ57-54)。本文的计算将会为研究斑岩铜矿及其它类型的硫化物矿床提供更有力的支撑。

1 计算方法

质量相关的同位素分馏是由同位素原子替换所产生的振动频率变化引起的(Bigeleisen and Mayer， 1947； Urey， 1947； Kieffer， 1982)。由于影响晶格能的其它潜在因素对大多数元素的同位素分馏影响很小(Schauble， 2011)，本文不予考虑。两种物质A和B之间的元素Y的同位素分馏系数αA-B是指物质A中元素Y的重、轻同位素数目之比除以物质B中相应的同位素数目之比，即：

αA-B=(nY*/nY)A/(nY*/nY)B

(1)

其中，nY*和nY分别对应的是元素Y的重同位素Y*和轻同位素Y 的原子数目。物质A与Y原子的理想气体之间的同位素分馏系数被称为物质A的简约配分函数比(βA)(Richetetal., 1977)：

βA= (nY*/nY)A/(nY*/nY)gas

(2)

因此，

αA-B=βA/βB

(3)

由于αA-B值通常接近于1，在实际应用中常用千分比来表示，即：

ΔA-B/‰= 103lnαA-B=103lnβA-103lnβB

(4)

如果物质A是晶体，那么它的简约配分函数比(βA)可以根据其简谐振动频率计算得出(Méheutetal., 2007， 2009； Blanchardetal., 2009)：

对于晶体结构中所含原子个数多于120的硫化物矿物，基于密度泛函微扰理论(DFPT)计算振动频谱难以实现。在这种情况下，简约配分函数比β可以根据原子间力常数计算得到(Bigeleisen and Mayer， 1947； Kowalski and Jahn， 2011； Kowalskietal., 2013； Schauble， 2011； Ducheretal., 2016)：

其中，Δm=m*-m，m为轻同位素原子的质量，m*为重同位素原子的质量；Fi为作用于同位素原子上的力常数，根据有限位移法计算得到。当满足以下条件时式(6)可以看作是式(5)的有效近似(Blanchardetal., 2017)： ① 在相对较高的温度下，即温度满足hυ/kT<2，υ为与同位素原子相关的振动频率，本文所含原子个数多于120的硫化物矿物中与同位素原子(即S和Fe)相关的振动频率均小于400 cm-1，因此适用温度高于290 K； ② 两种同位素原子之间的质量差远小于平均原子质量，这一条对于S和Fe都是满足的； ③ 假设原子间力常数不受同位素原子替换的影响。公式(6)的有效性已经被第一性原理计算证实： Kowalski等 (2011) 计算了十字石(晶胞中含81个原子)和锂辉石(晶胞中含80个原子)的Li同位素分馏，发现公式(6)计算的103lnβ7-6与公式(5)计算的103lnβ7-6几乎完全相等； Liu等 (2021) 的计算显示公式(6)计算的25℃下铜矾(晶胞中含64个原子)和水胆矾(晶胞中含84个原子)的103lnβ65-63分别比公式(5)的计算结果低0.03‰和高0.06‰。这表明对于本文所含原子个数多于120的硫化物矿物，公式(6)也是式(5)的有效近似。

表1 不同硫化物矿物用于第一性原理计算的K点网格、q点网格及加密的q点网格

2 计算结果

采用第一性原理计算得到的辉铜矿、铜蓝、黑硫铜镍矿、黄铜矿、方黄铜矿和斑铜矿的晶体结构已在Liu等(2021)前期的研究中给出，计算结果与实验数据有很好的一致性，误差不超过2%，且声子频率也与实验测定结果吻合的很好。根据计算的声子频率与实验的差异可以估计β系数的误差，但是由于本文研究的部分硫化物如辉铜矿、方黄铜矿和斑铜矿缺少实验数据，而且不同实验的结果差别较大，因此很难根据声子频率估计β系数的误差。但是研究表明PBE对声子频率的低估一般不会超过5%，而声子频率低估5%将导致103lnβ低估约5%至10%(Méheutetal., 2007， 2009)。

2.1 含Cu硫化物的S同位素分馏

本文基于Liu等(2021)之前优化好的晶体结构来计算式(5)中所需要的声子频率。计算了0～1 000℃之间的S同位素简约配分函数比(103lnβ34-32)，并采用3次多项式拟合β系数与温度之间的函数关系，拟合系数见表2。如图1所示，34S的富集顺序为： 铜蓝>方黄铜矿>黄铜矿≈黑硫铜镍矿>斑铜矿>辉铜矿。与辉铜矿相比，100℃时铜蓝、方黄铜矿、黄铜矿、黑硫铜镍矿和斑铜矿中的34S含量分别高2.86‰、2.48‰、2.25‰、2.21‰和0.39‰。

表2 含Cu硫化物的S同位素简约配分函数比与温度关系的拟合参数

图1 含Cu硫化物的S同位素简约配分函数比与温度的关系

2.2 辉铜矿和斑铜矿同质多像体的S同位素分馏

作为重要的铜矿石矿物，辉铜矿和斑铜矿广泛存在于斑岩铜矿和其他地质环境中(Berryetal.， 1983)，并且都具有随温度变化的同质多像变体(Makovicky， 2006)。通常用γ、β和α相来表示辉铜矿的3种同质多像变体(Wang, 2012)，用低温、中温和高温来表示斑铜矿的3种同质多像变体(Dingetal., 2005)。γ-辉铜矿在自然界最常见，低于103℃时稳定，103℃时转变为β-辉铜矿，435℃时转变为α-辉铜矿(Fleet, 2006)。低温斑铜矿在常温常压下稳定存在(Grguricetal., 2000)，200℃时转变为中温斑铜矿，265℃时转变为高温斑铜矿(Dingetal., 2005)。由于Cu2S和Cu5FeS4同质多像变体在铜矿床中非常常见，所以计算它们的S同位素分馏系数对于理解由相变产生的S同位素分馏并解释自然界中的S同位素在不同物质中的分布具有重要意义。斑铜矿高温和中温变体的晶体结构中Cu原子的分布是无序的，Ding等(2005)给出了中温变体的一种可能的有序立方结构Cu8Fe4S8。为了突出成分和结构对同位素分馏影响的区别，本文也计算了Cu8Fe4S8的同位素分馏性质。

辉铜矿和斑铜矿同质多像体的103lnβ34-32随温度的变化如图2所示， 与温度关系的拟合参数见表3。由图2可知，34S在这5种硫化物中的富集顺序为β-辉铜矿>Cu8Fe4S8>α-辉铜矿>中温斑铜矿≈低温斑铜矿>高温斑铜矿>γ-辉铜矿。对比图1可知辉铜矿相变引起的S同位素分馏比其它成分不同的硫化物之间的分馏还要大，在103℃，γ-辉铜矿转变为β-辉铜矿时产生的S同位素分馏为3.09‰；在435℃，β-辉铜矿转变为α-辉铜矿时产生的S同位素分馏为0.53‰。与辉铜矿相比，斑铜矿相变时产生的S同位素分馏非常小。200℃时， Cu8Fe4S8与中温斑铜矿103lnβ34-32的差别为1.12‰。

图2 辉铜矿和斑铜矿同质多像体的S同位素简约配分函数比与温度的关系

表3 辉铜矿和斑铜矿同质多像体的S同位素简约配分函数比与温度关系的拟合参数

2.3 Cu-Fe硫化物的Fe同位素分馏

计算了0～1 000℃之间Cu-Fe硫化物的Fe同位素简约配分函数比(103lnβ57-54)，并采用103lnβ57-54=a(106/T2)+b(106/T2)2+c(106/T2)3拟合103lnβ57-54与温度之间的函数关系，拟合系数见表4。如图3所示57Fe在Cu-Fe硫化物之间的富集顺序为：方黄铜矿≈黄铜矿>低温斑铜矿>高温斑铜矿>中温斑铜矿>Cu8Fe4S8。与斑铜矿(低温变体)相比，25℃时黄铜矿和方黄铜矿的57Fe含量分别高1.43‰和1.58‰。对比图1、2、3可知，黄铜矿与方黄铜矿之间的Fe同位素分馏与S同位素分馏类似，几乎不发生分馏；但是斑铜矿之间却有很大的差别，例如低温变体与中温变体25℃时103lnβ57-54的差别为1.07‰。

表4 Cu-Fe硫化物的Fe同位素简约配分函数比与温度关系的拟合参数

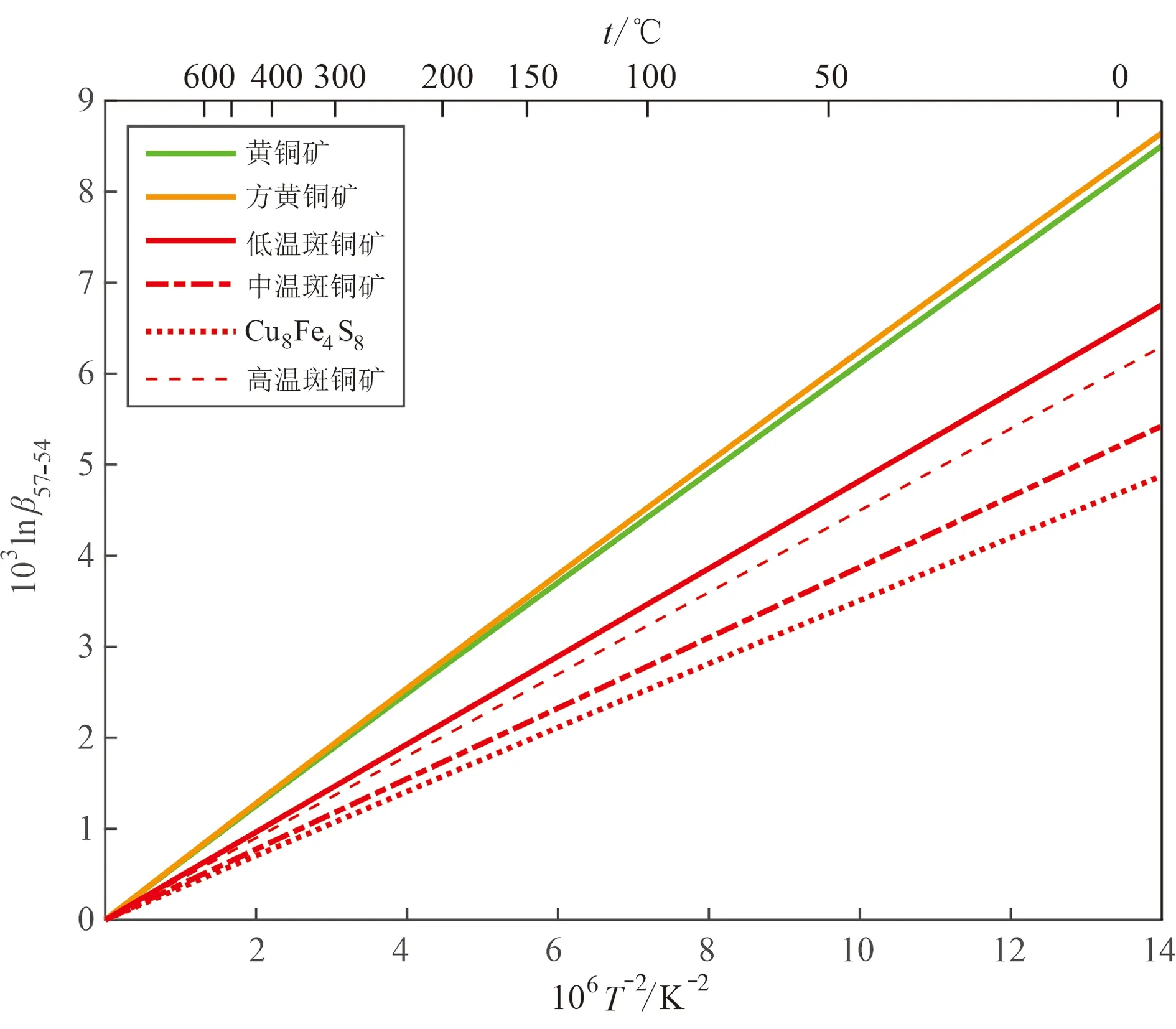
图3 Cu-Fe硫化物的Fe同位素简约配分函数比与温度的关系

已有研究者基于NRIXS数据预测了黄铜矿的Fe同位素简约配分函数比(103lnβ57-54)(Polyakov and Soultanov, 2011； Dauphasetal., 2012)。本文计算的不同温度下黄铜矿的103lnβ57-54与前人研究结果的对比见图4。由图4可知，即使基于相同的NRIXS数据，采用不同方法计算的103lnβ57-54也有很大的差别，本文的计算结果与Dauphas等(2012)采用新方法计算的103lnβ57-54有很好的一致性。

图4 黄铜矿的Fe同位素简约配分函数比与前人计算结果的对比

3 讨论

3.1 键长对含Cu硫化物中S同位素分馏的影响

矿物的同位素性质在很大程度上取决于同位素原子的配位数、氧化态及成键性质。一般而言，配位数越小越容易富集重同位素(Schauble， 2004)；氧化态越高越容易富集重同位素(O’Neil， 1977)；原子之间的键长越短，键强度越大，越容易富集重同位素(Zheng， 1995)。然而，同位素原子的配位数对分馏的控制作用对本文所研究的含Cu硫化物的S同位素分馏并不适用。比如，β-辉铜矿中S原子的配位数为5，黑硫铜镍矿、黄铜矿和方黄铜矿中S原子的配位数为4，而β-辉铜矿的103lnβ34-32却大于黑硫铜镍矿、黄铜矿和方黄铜矿的103lnβ34-32。在含Cu的硫化物中，S的氧化态的控制作用也不适用，比如γ-Cu2S(S为-2价)的103lnβ34-32大于CuS2(S为-1价)的103lnβ34-32。

在α、β和γ相辉铜矿中，S原子只与Cu原子形成Cu—S键；在黑硫铜镍矿中，S原子除了与Cu原子形成Cu—S键以外，还可以与另一个S原子形成S—S键；在铜蓝中，5次配位的S原子只与Cu原子形成Cu—S键，4次配位的S原子与3个Cu原子、另外1个S原子分别形成Cu—S键和S—S键；在Cu-Fe硫化物中，S原子既与Cu原子形成Cu—S键又与Fe原子形成Fe—S键。含Cu硫化物的金属-S平均键长见表5，可以看出本文的计算结果与实验结果吻合得很好，误差不超过1.3%。表5中没有列出β-辉铜矿、α-辉铜矿、中温斑铜矿和高温斑铜矿实验测量的键长，是因为实验给出的晶体结构中Cu原子的排列是无序的； Cu8Fe4S8的实验测量的键长也没列出的原因是它的晶体结构是基于计算推测的(Dingetal., 2005)。

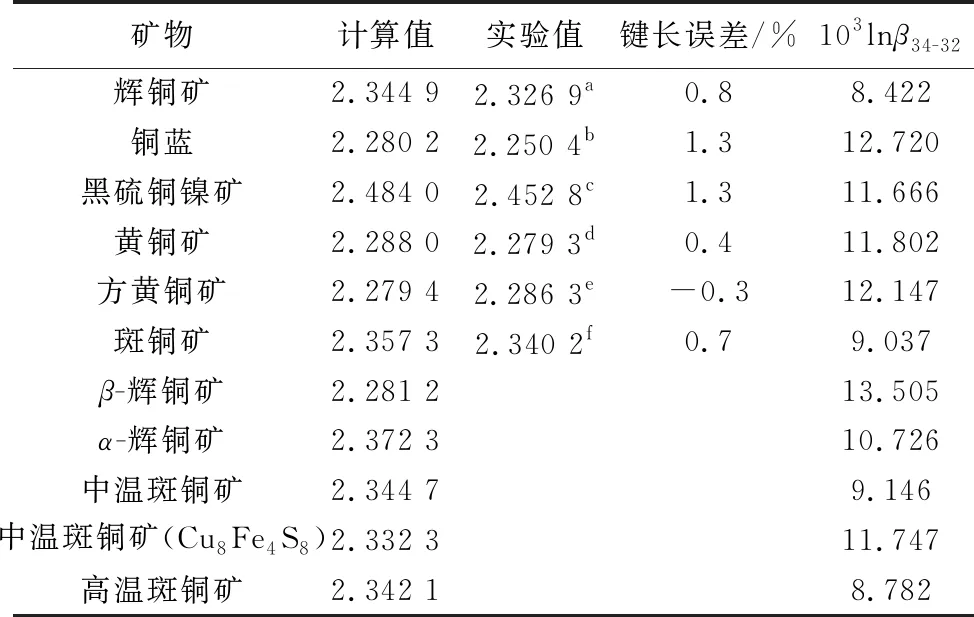
表5 含Cu硫化物的金属-S平均键长及25℃时的103lnβ34-32

图5给出了金属-S平均键长与103lnβ34-32之间的关系，从整体上来说金属-S平均键长与103lnβ34-32没有明显的相关性，即使考虑S原子所形成的所有化学键的平均键长，这种弱相关性也没有得到改善。对于配位数相同的含Cu硫化物，金属-S平均键长与103lnβ34-32也没有明显的相关性。例如，S原子配位数都为4的黑硫铜镍矿和黄铜矿，Cu—S平均键长相差很大，而103lnβ34-32却基本相同；α和γ相辉铜矿的S原子配位数都为6，α相的Cu—S平均键长略大于γ相的，而α相的103lnβ34-32却远大于γ相的。

3.2 键长对Cu-Fe硫化物中Fe同位素分馏的影响

本文研究的Cu-Fe硫化物中Fe原子的配位数都为4，因此研究这些硫化物中Fe同位素分馏的影响因素时可以忽略Fe原子的配位数。Cu-Fe硫化物中Fe—S键的平均键长见表6，可以看出计算值与实验值吻合得很好，误差不超过0.3%。图6给出了Cu-Fe硫化物中Fe—S平均键长与103lnβ57-54之间的关系。如图6所示，103lnβ57-54与Fe—S平均键长基本成线性负相关关系。然而，它们的103lnβ34-32却与金属-S平均键长没有明显的相关性(图5)，这表明化学键的键长不是控制硫化物中S同位素分馏的主要因素，也反应了硫化物中S同位素分馏的控制因素的复杂性。

图5 铜的硫化物的金属-S平均键长与25℃时的103lnβ34-32之间的关系

表6 Cu-Fe硫化物的Fe—S平均键长及25℃ 时的103lnβ57-54

图6 Cu-Fe硫化物的Fe—S平均键长与25℃ 时的103lnβ57-54之间的关系

3.3 地质应用

本文研究的含Cu硫化物几乎都可以在斑岩铜矿中出现(Riverosetal., 2014； 欧阳学财等， 2017； 刘宝山等， 2020； 杨志明等， 2020)。作为斑岩铜矿中最重要的原生矿石矿物，黄铜矿的S同位素特征已得到广泛研究(Kimetal., 2019； Heetal., 2020；Tangetal., 2020)。黄铜矿经蚀变后会转变为次生含Cu矿物如铜的硫酸盐和碳酸盐(Mathuretal., 2009)。在斑岩铜矿的形成与演化过程中黄铜矿是一直存在的(Sillitoe， 2010)，可以与多种原生含Cu矿物和次生含Cu矿物共生，因此黄铜矿与其它含Cu矿物之间的S同位素分馏系数可以为研究斑岩铜矿的形成与演化提供约束。本文计算的含铜矿物的S同位素分馏系数结合我们之前计算的黄铁矿、方铅矿、闪锌矿等硫化物的S同位素分馏系数(Liuetal., 2015， 2016， 2018)，将会为研究斑岩铜矿及其它类型的硫化物矿床提供更全面的理论数据。

此外，本文的计算表明黄铜矿比斑铜矿更为富集重Fe同位素，但是印度洋卧蚕1号热液区2个样品中黄铜矿的δ56Fe(-0.99‰、-1.09‰)小于斑铜矿的δ56Fe(0.10‰、-0.69‰)(Wangetal., 2021)，这表明Fe同位素分馏在这两种矿物中未达到平衡。Blanchard等(2009)采用与本文相同的贋势计算了黄铁矿的Fe同位素简约配分函数比(103lnβ57-54)，与计算的黄铜矿相比，25℃时黄铁矿的103lnβ57-54高6.17‰。因此，铜山口铜钼矿岩脉中一些黄铁矿样品的δ57Fe小于共生黄铜矿的δ57Fe(Heetal., 2020)，是由于黄铁矿与黄铜矿之间Fe同位素的非平衡分馏。硫同位素分馏系数最主要的应用之一就是地温计。同样，共生硫化物对之间的Fe同位素分馏也可以作为地温计，例如随着温度从800℃降低到25℃黄铁矿与黄铜矿之间的Fe同位素分馏从0.49‰升高到6.18‰，随着温度从800℃降低到265℃黄铁矿与高温斑铜矿之间的Fe同位素分馏从0.65‰升高到2.55‰。目前的Fe同位素分析测试技术可以测量出这些分馏值(秦燕等， 2020)。

虽然硫化物中的S同位素分馏在研究矿床的形成和演化、地幔交代、壳幔混染等多种地质过程中起着重要作用，但是在一些情况下，仅仅依靠S同位素来约束地质过程存在不确定性，例如用δ34S来确定与科马提岩有关的矿床的硫源 (Hiebertetal., 2016)。随着同位素分析测试技术的发展，Cu-S同位素联合(杨立飞等， 2016； 欧阳学财， 2017)、Fe-S同位素联合(Heetal., 2020； Rayetal., 2021)、Fe-Cu同位素联合(Grahametal., 2004)等已被用来约束矿床成因，且取得了很好的效果。对于含Cu矿物的Cu同位素分馏，已做了相关研究(Liuetal., 2021)。可以发现S、Fe和Cu同位素在这些含Cu矿物中的分馏情况大不相同，含Cu矿物不同温度下S、Fe和Cu同位素分馏系数的确定可以为利用Cu-Fe-S同位素联合约束地质过程提供更直接、更有力的支撑。

4 结论

(1) 基于第一性原理计算确定了含Cu硫化物中的S同位素分馏，重S同位素在这些矿物中的富集顺序为铜蓝>方黄铜矿>黄铜矿≈黑硫铜镍矿>斑铜矿>辉铜矿。含Cu硫化物中的S同位素分馏与S原子的配位数、金属-S平均键长、S原子形成的所有化学键的平均键长没有明显的相关性。

(2) 计算了辉铜矿及斑铜矿同质多像体的S同位素分馏，结果表明辉铜矿相变引起的S同位素分馏特别大，尤其是γ-辉铜矿转变为β-辉铜矿时S同位素分馏可达3.09‰；而斑铜矿相变时产生的S同位素分馏却可以忽略不计。

(3) 计算的黄铜矿的103lnβ57-54与前人的结果吻合得非常好，重Fe同位素在Cu-Fe硫化物之间的富集顺序为方黄铜矿≈黄铜矿>低温斑铜矿>高温斑铜矿>中温斑铜矿>Cu8Fe4S4，103lnβ57-54与Fe—S平均键长基本成线性负相关关系。

(4) 本文的计算结果能够在一定程度上解释斑岩铜矿中的S、Fe同位素组成，与之前的研究结果结合起来可以成为潜在的S同位素地温计和Fe同位素地温计，可以为利用Cu-Fe-S同位素联合约束地质过程提供依据。

致谢衷心感谢审稿人对本文提出的宝贵意见。